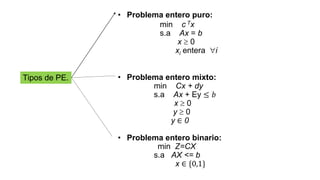
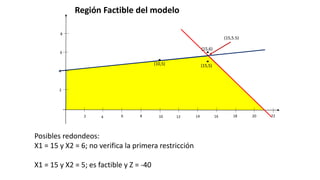
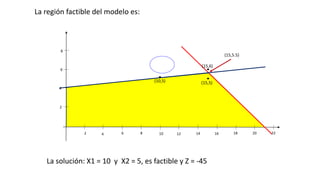
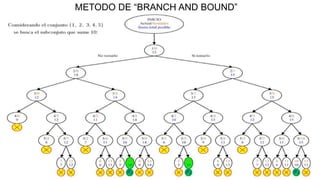
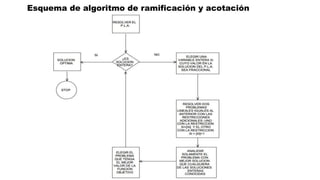
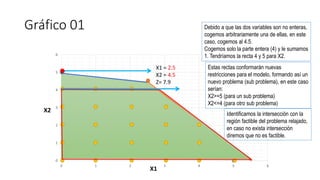
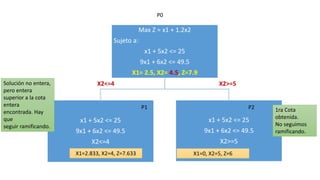
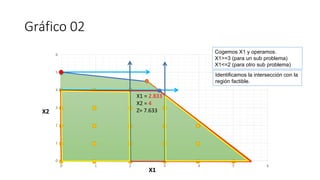
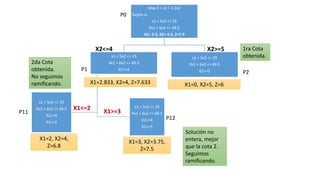
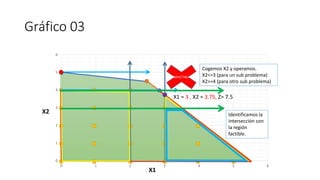
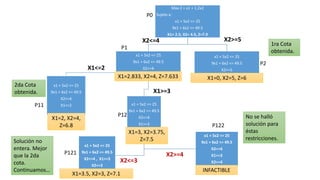
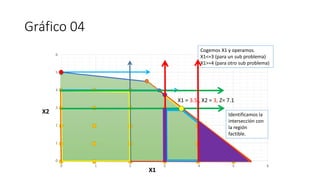
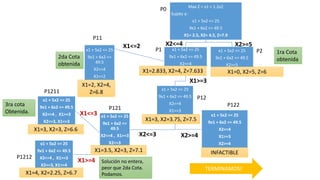
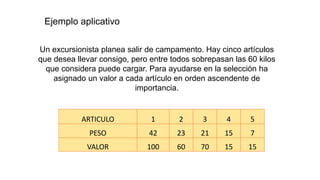
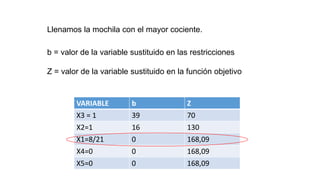
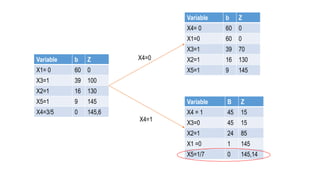
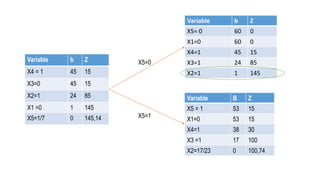
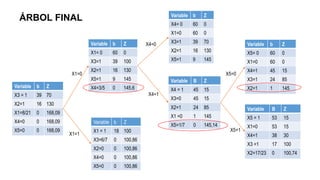
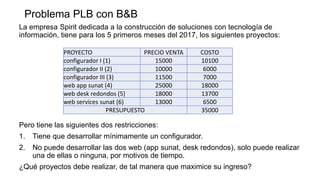
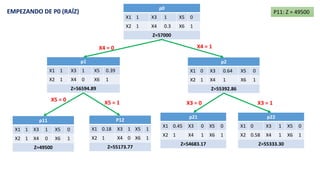
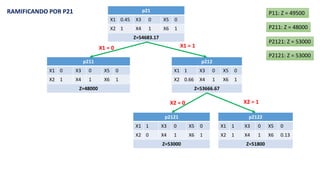
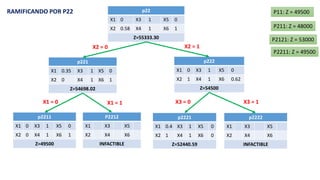
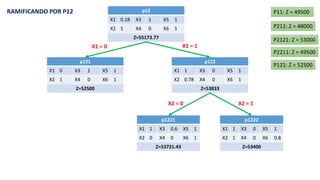
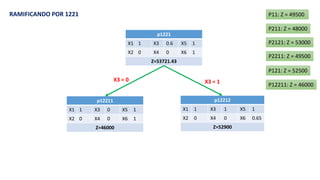
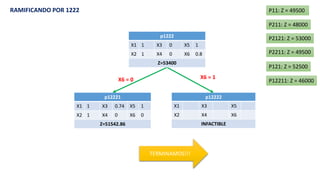
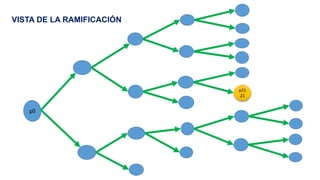
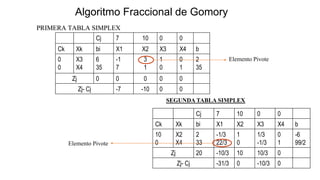
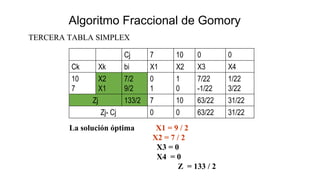
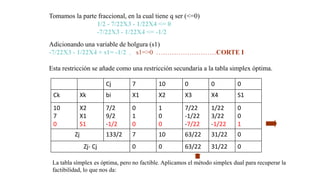
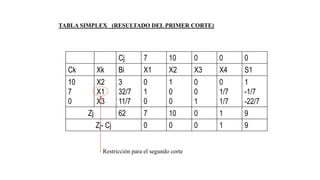
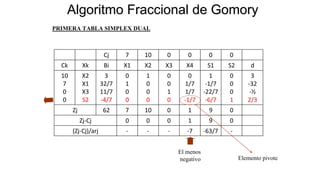
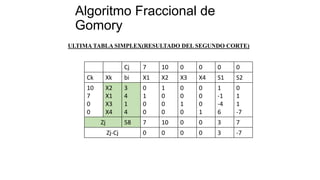
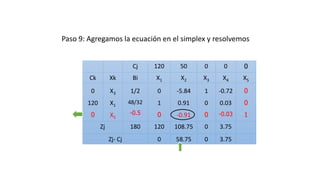
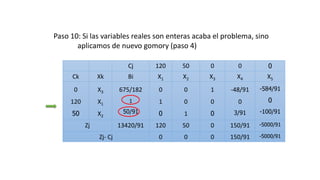
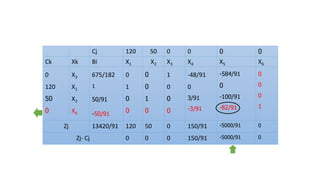
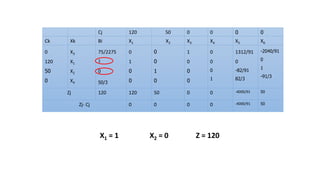
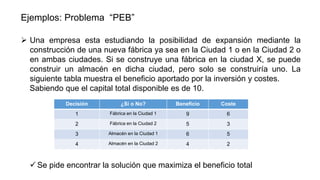
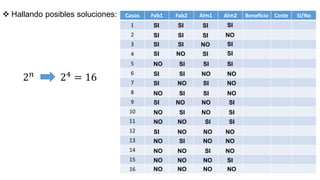
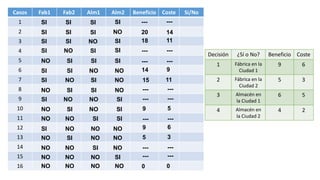
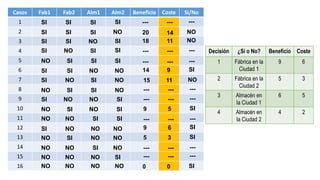
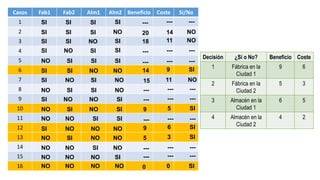
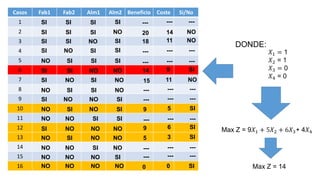
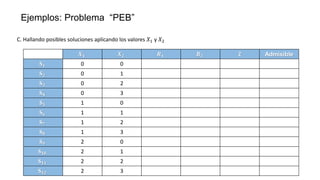
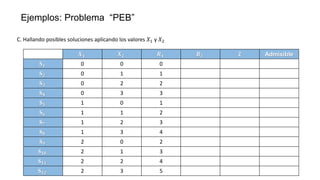
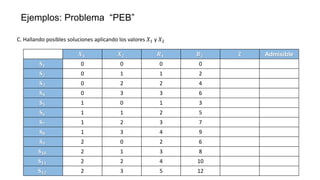
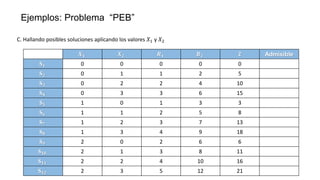
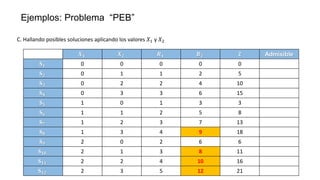
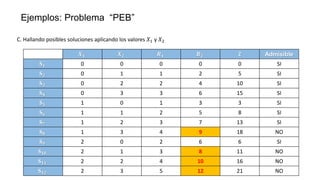
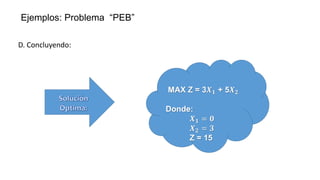
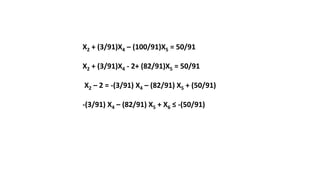El documento aborda la programación entera, incluyendo técnicas como ramificación y acotamiento, y el método de corte Gomory, aplicándolo a problemas prácticos como la optimización de la producción de lápices y la selección de artículos para llevar en una mochila. Se detalla la formulación de problemas con variables enteras y mixta, ilustrando cómo encontrar soluciones óptimas mediante el método de 'branch and bound'. Finalmente, se presentan ejemplos concretos que demuestran la aplicación de estas técnicas en contextos reales.

1. Carlos A. Bruno Romero
PROGRAMACIÓN
ENTERA

2. CONTENIDO
• PROGRAMACIÓN ENTERA
• RAMIFICACIÓN Y ACOTAMIENTO
• PLANO DE CORTE GOMORY
• Método de Enumeración Exhaustiva o Explícita
• SOFTWARE’S: WinQSB y EXCEL (Solver)

3. PROGRAMACIÓN ENTERA
Muchos de los problemas reales las variables sólo
pueden tomar valores enteros
Ejemplo:
* Compras, personas, decisiones de inversión, etc.
Método Simplex?
• Cómo saber si tenemos una solución?
• Soluciones no están en los vértices

4. • Problema entero puro:
min c Tx
s.a Ax = b
x  0
xi entera i
• Problema entero mixto:
min Cx + dy
s.a Ax + Ey ≤ 𝑏
x  0
y  0
y ∈ 0
• Problema entero binario:
min Z=CX
s.a AX <= b
x ∈ {0,1}
Tipos de PE.

5. Podemos aceptar una solución aproximada?
Consideremos el siguiente problema de programación lineal
entera
Min Z = X1 – 11X2
S.a:
-X1 + 10X2 ≤ 40
10X1 + 10X2 ≤ 205
X1, X2 ≥ 0 y enteras
Solución optima sin considerar las condiciones de integridad:
X1 = 15 y X2 = 5.5

6. 2 4 6 8 10 12 14 16 18 20 22
2
4
6
8
(15,6)
(10,5) (15,5)
(15,5.5)
Región Factible del modelo
Posibles redondeos:
X1 = 15 y X2 = 6; no verifica la primera restricción
X1 = 15 y X2 = 5; es factible y Z = -40

7. 2 4 6 8 10 12 14 16 18 20 22
2
4
6
8
(15,6)
(10,5) (15,5)
(15,5.5)
La región factible del modelo es:
La solución: X1 = 10 y X2 = 5, es factible y Z = -45

8. METODO DE “BRANCH AND BOUND”

9. Esquema de algoritmo de ramificación y acotación

10. PROBLEMA PLP con B&B
Una empresa fabrica dos modelos de lápiz de grafito, el modelo HB Y 2B,
con un beneficio de 1 sol y 1.2 sol respectivamente.
El modelo HB es el más largo, especial para estudiantes, para su
fabricación requiere 1 gr de grafito y 9m3 de madera de enebro.
Por otro lado, el modelo 2B, más pequeño y un trazo más condensado,
especial para dibujar, requiere de 5gr de grafito y 6m3 de enebro.
Sabiendo que se cuenta 25 gr de grafito y 49.5m3 de madera de enebro.
¿Cuántos lápices de modelos HB y 2B se deben fabricar, sabiendo que se
pretende maximizar los benéficos?

11. Modelo
Variables de decisión
x1: Cantidad de lápices del modelo HB a fabricar.
x2: Cantidad de lápices del modelo 2B a fabricar.
Función objetivo:
Max Z = x1 + 1.2x2
Restricciones
x1 + 5x2 <= 25 (Cantidad de grafito en gramos)
9x1 + 6x2 <= 49.5 (Cantidad de madera de enebro en m3)
x1, x2 >= 0, enteros

12. Gráfico 01
0
1
2
3
4
5
6
0 1 2 3 4 5 6
X1 = 2.5
X2 = 4.5
Z= 7.9
X2
X1
Debido a que las dos variables son no enteras,
cogemos arbitrariamente una de ellas, en este
caso, cogemos al 4.5.
Cogemos solo la parte entera (4) y le sumamos
1. Tendríamos la recta 4 y 5 para X2.
Estas rectas conformarán nuevas
restricciones para el modelo, formando así un
nuevo problema (sub problema), en este caso
serían:
X2>=5 (para un sub problema)
X2<=4 (para otro sub problema)
Identificamos la intersección con la
región factible del problema relajado,
en caso no exista intersección
diremos que no es factible.

13. Max Z = x1 + 1.2x2
Sujeto a:
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X1= 2.5, X2= 4.5, Z=7.9
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2>=5
P0
P1 P2
X2<=4 X2>=5
X1=2.833, X2=4, Z=7.633 X1=0, X2=5, Z=6
1ra Cota
obtenida.
No seguimos
ramificando.
Solución no entera,
pero entera
superior a la cota
entera
encontrada. Hay
que
seguir ramificando.

14. Gráfico 02
0
1
2
3
4
5
6
0 1 2 3 4 5 6
X2
X1
X1 = 2.833
X2 = 4
Z= 7.633
Cogemos X1 y operamos.
X1>=3 (para un sub problema)
X1<=2 (para otro sub problema)
Identificamos la intersección con la
región factible.

15. Max Z = x1 + 1.2x2
Sujeto a:
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X1= 2.5, X2= 4.5, Z=7.9
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
X1>=3
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
X1<=2
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2>=5
P1 P2
X2<=4 X2>=5
X1=2.833, X2=4, Z=7.633 X1=0, X2=5, Z=6
P0
X1<=2
X1>=3
P11
P12
X1=2, X2=4,
Z=6.8
X1=3, X2=3.75,
Z=7.5
2da Cota
obtenida.
No seguimos
ramificando.
Solución no
entera, mejor
que la cota 2.
Seguimos
ramificando.
1ra Cota
obtenida.

16. Gráfico 03
0
1
2
3
4
5
6
0 1 2 3 4 5 6
X2
X1
X1 = 3 , X2 = 3.75, Z= 7.5
Cogemos X2 y operamos.
X2<=3 (para un sub problema)
X2>=4 (para otro sub problema)
INFACTIBLE
Identificamos la
intersección con
la región
factible.

17. Max Z = x1 + 1.2x2
Sujeto a:
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X1= 2.5, X2= 4.5, Z=7.9
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
X1>=3
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4 , X1>=3
X2<=3
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
X1>=3
X2>=4
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
X1<=2
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2>=5
P1
P2
X2<=4 X2>=5
X1=2.833, X2=4, Z=7.633 X1=0, X2=5, Z=6
P0
X1<=2
X1>=3
P11
P12
X1=2, X2=4,
Z=6.8
X1=3, X2=3.75,
Z=7.5
P121
P122
X2<=3
X2>=4
X1=3.5, X2=3, Z=7.1
INFACTIBLE
1ra Cota
obtenida.
2da Cota
obtenida.
Solución no
entera. Mejor
que la 2da
cota.
Continuamos…
No se halló
solución para
éstas
restricciones.

18. Gráfico 04
0
1
2
3
4
5
6
0 1 2 3 4 5 6
X2
X1
X1 = 3.5 , X2 = 3, Z= 7.1
Cogemos X1 y operamos.
X1<=3 (para un sub problema)
X1>=4 (para otro sub problema)
Identificamos la
intersección con
la región
factible.

19. Max Z = x1 + 1.2x2
Sujeto a:
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X1= 2.5, X2= 4.5, Z=7.9
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
X1>=3
x1 + 5x2 <= 25
9x1 + 6x2 <=
49.5
X2<=4 , X1>=3
X2<=3
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4 , X1>=3
X2<=3, X1>=4
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4 , X1>=3
X2<=3, X1<=3
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
X1>=3
X2>=4
x1 + 5x2 <= 25
9x1 + 6x2 <=
49.5
X2<=4
X1<=2
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2>=5
P1 P2
X2<=4 X2>=5
X1=2.833, X2=4, Z=7.633 X1=0, X2=5, Z=6
P0
X1<=2
X1>=3
P11
P12
X1=2, X2=4,
Z=6.8
X1=3, X2=3.75, Z=7.5
P121
P122
X2<=3 X2>=4
X1=3.5, X2=3, Z=7.1 INFACTIBLE
1ra Cota
obtenida
2da Cota
obtenida
X1<=3
X1>=4
X1=3, X2=3, Z=6.6
X1=4, X2=2.25, Z=6.7
3ra cota
Obtenida.
P1211
P1212
Solución no entera,
peor que 2da Cota.
Podamos.
TERMINAMOS!

20. Finalizando el proceso de ramificación y poda,
para el e
La solución óptima entera corresponde al sub problema P11
Max Z = x1 + 1.2x2
x1 + 5x2 <= 25
9x1 + 6x2 <= 49.5
X2<=4
X1<=2
La solución óptima es:
Fabricar 2 lápices del modelo HB y 4 lápices del
modelo 2B.
Obteniendo un ingreso total de 6.8 Soles.

21. Es un método muy parecido al de ramificación y
acotamiento para modelos mixtos y puros. Sin embargo
las variables solo pueden tomar el valor de x ∈ 0,1
Ejemplo:
• Asignación
• Tipo mochila
• Casamentero
• Método Aditivo de Egón Balas
PROGRAMACIÓN ENTERA BINARIA

22. Un excursionista planea salir de campamento. Hay cinco artículos
que desea llevar consigo, pero entre todos sobrepasan las 60 kilos
que considera puede cargar. Para ayudarse en la selección ha
asignado un valor a cada artículo en orden ascendente de
importancia.
ARTICULO 1 2 3 4 5
PESO 42 23 21 15 7
VALOR 100 60 70 15 15
Ejemplo aplicativo

23. MAX Z= 100 X1 + 60 X2 + 70 X3 + 15 X4 + 15 X5
S.A
42 X1 + 23 X2 + 21 X3 + 15 X4 + 7 X6 <= 60
Calculamos los ci/ai
OBJETO Ci/ai
1 100/42 = 2,38
2 60/23 = 2,61
3 70/21 = 3,33
4 15/15 = 1
5 15/7 = 2,14

24. Llenamos la mochila con el mayor cociente.
b = valor de la variable sustituido en las restricciones
Z = valor de la variable sustituido en la función objetivo
VARIABLE b Z
X3 = 1 39 70
X2=1 16 130
X1=8/21 0 168,09
X4=0 0 168,09
X5=0 0 168,09

25. Variable b Z
X3 = 1 39 70
X2=1 16 130
X1=8/21 0 168,09
X4=0 0 168,09
X5=0 0 168,09
Variable b Z
X1= 0 60 0
X3=1 39 100
X2=1 16 130
X5=1 9 145
X4=3/5 0 145,6
Variable b Z
X1 = 1 18 100
X3=6/7 0 100,86
X2=0 0 100,86
X4=0 0 100,86
X5=0 0 100,86
X1=0
X1=1

26. Variable b Z
X1= 0 60 0
X3=1 39 100
X2=1 16 130
X5=1 9 145
X4=3/5 0 145,6
Variable b Z
X4= 0 60 0
X1=0 60 0
X3=1 39 70
X2=1 16 130
X5=1 9 145
Variable B Z
X4 = 1 45 15
X3=0 45 15
X2=1 24 85
X1 =0 1 145
X5=1/7 0 145,14
X4=0
X4=1

27. Variable b Z
X4 = 1 45 15
X3=0 45 15
X2=1 24 85
X1 =0 1 145
X5=1/7 0 145,14
Variable b Z
X5= 0 60 0
X1=0 60 0
X4=1 45 15
X3=1 24 85
X2=1 1 145
Variable B Z
X5 = 1 53 15
X1=0 53 15
X4=1 38 30
X3 =1 17 100
X2=17/23 0 100,74
X5=0
X5=1

28. Solución Optima
X1= 0
X2= 1
X3= 1
X4= 0
X5= 1
Z=145
Se llevara en la mochila los objetos 2, 3 y 5. Con
un valor de 145 y un peso de 51 kilos

29. Variable b Z
X3 = 1 39 70
X2=1 16 130
X1=8/21 0 168,09
X4=0 0 168,09
X5=0 0 168,09
Variable b Z
X1= 0 60 0
X3=1 39 100
X2=1 16 130
X5=1 9 145
X4=3/5 0 145,6
Variable b Z
X1 = 1 18 100
X3=6/7 0 100,86
X2=0 0 100,86
X4=0 0 100,86
X5=0 0 100,86
X1=0
X1=1
Variable b Z
X4= 0 60 0
X1=0 60 0
X3=1 39 70
X2=1 16 130
X5=1 9 145
Variable B Z
X4 = 1 45 15
X3=0 45 15
X2=1 24 85
X1 =0 1 145
X5=1/7 0 145,14
X4=0
X4=1
Variable b Z
X5= 0 60 0
X1=0 60 0
X4=1 45 15
X3=1 24 85
X2=1 1 145
Variable B Z
X5 = 1 53 15
X1=0 53 15
X4=1 38 30
X3 =1 17 100
X2=17/23 0 100,74
X5=0
X5=1
ÁRBOL FINAL

30. Problema PLB con B&B
La empresa Spirit dedicada a la construcción de soluciones con tecnología de
información, tiene para los 5 primeros meses del 2017, los siguientes proyectos:
Pero tiene las siguientes dos restricciones:
1. Tiene que desarrollar mínimamente un configurador.
2. No puede desarrollar las dos web (app sunat, desk redondos), solo puede realizar
una de ellas o ninguna, por motivos de tiempo.
¿Qué proyectos debe realizar, de tal manera que maximice su ingreso?
PROYECTO PRECIO VENTA COSTO
configurador I (1) 15000 10100
configurador II (2) 10000 6000
configurador III (3) 11500 7000
web app sunat (4) 25000 18000
web desk redondos (5) 18000 13700
web services sunat (6) 13000 6500
PRESUPUESTO 35000

31. Modelo
Variables de decisión
xi 1: Sí el proyecto i se debe realizar.
0: No debe realizarse el proyecto i.
i= {1,2,3,4,5,6}
Función objetivo:
Max Z = 15000x1+10000x2+11500x3+25000x4+18000x5+13000x6
Restricciones
10100x1+6000x2+7000x3+18000x4+13700x5+6500x6 <= 35000 (presupuesto)
x1, x2, x3, x4, x5, x6 : {0,1}
Mínimamente un configurador
X1 + X2 + X3 >= 1
Una de las web (app sunat, desk redondos) o ninguna, pero no las dos
x4 + x5 <=1

32. p0
X1 1 X3 1 X5 0
X2 1 X4 0.3 X6 1
Z=57000
p1
X1 1 X3 1 X5 0.39
X2 1 X4 0 X6 1
Z=56594.89
p2
X1 0 X3 0.64 X5 0
X2 1 X4 1 X6 1
Z=55392.86
p11
X1 1 X3 1 X5 0
X2 1 X4 0 X6 1
Z=49500
P12
X1 0.18 X3 1 X5 1
X2 1 X4 0 X6 1
Z=55173.77
p22
X1 0 X3 1 X5 0
X2 0.58 X4 1 X6 1
Z=55333.30
p21
X1 0.45 X3 0 X5 0
X2 1 X4 1 X6 1
Z=54683.17
X4 = 0
X5 = 0
X5 = 1
X4 = 1
X3 = 0 X3 = 1
EMPEZANDO DE P0 (RAÍZ) P11: Z = 49500

33. p21
X1 0.45 X3 0 X5 0
X2 1 X4 1 X6 1
Z=54683.17
p211
X1 0 X3 0 X5 0
X2 1 X4 1 X6 1
Z=48000
p212
X1 1 X3 0 X5 0
X2 0.66 X4 1 X6 1
Z=53666.67
p2122
X1 1 X3 0 X5 0
X2 1 X4 1 X6 0.13
Z=51800
p2121
X1 1 X3 0 X5 0
X2 0 X4 1 X6 1
Z=53000
X1 = 0 X1 = 1
X2 = 0 X2 = 1
RAMIFICANDO POR P21 P11: Z = 49500
P211: Z = 48000
P2121: Z = 53000
P2121: Z = 53000

34. p22
X1 0 X3 1 X5 0
X2 0.58 X4 1 X6 1
Z=55333.30
p221
X1 0.35 X3 1 X5 0
X2 0 X4 1 X6 1
Z=54698.02
p222
X1 0 X3 1 X5 0
X2 1 X4 1 X6 0.62
Z=54500
p2211
X1 0 X3 1 X5 0
X2 0 X4 1 X6 1
Z=49500
P2212
X1 X3 X5
X2 X4 X6
INFACTIBLE
p2222
X1 X3 X5
X2 X4 X6
INFACTIBLE
p2221
X1 0.4 X3 1 X5 0
X2 1 X4 1 X6 0
Z=52440.59
X2 = 0
X1 = 0 X1 = 1
X2 = 1
X3 = 0 X3 = 1
RAMIFICANDO POR P22 P11: Z = 49500
P211: Z = 48000
P2211: Z = 49500
P2121: Z = 53000

35. p12
X1 0.18 X3 1 X5 1
X2 1 X4 0 X6 1
Z=55173.77
p121
X1 0 X3 1 X5 1
X2 1 X4 0 X6 1
Z=52500
p122
X1 1 X3 0 X5 1
X2 0.78 X4 0 X6 1
Z=53833
p1222
X1 1 X3 0 X5 1
X2 1 X4 0 X6 0.8
Z=53400
p1221
X1 1 X3 0.6 X5 1
X2 0 X4 0 X6 1
Z=53721.43
X1 = 0 X1 = 1
X2 = 0 X2 = 1
RAMIFICANDO POR P12 P11: Z = 49500
P211: Z = 48000
P2211: Z = 49500
P121: Z = 52500
P2121: Z = 53000

36. p1221
X1 1 X3 0.6 X5 1
X2 0 X4 0 X6 1
Z=53721.43
p12211
X1 1 X3 0 X5 1
X2 0 X4 0 X6 1
Z=46000
p12212
X1 1 X3 1 X5 1
X2 0 X4 0 X6 0.65
Z=52900
X3 = 0 X3 = 1
RAMIFICANDO POR 1221 P11: Z = 49500
P211: Z = 48000
P2211: Z = 49500
P121: Z = 52500
P2121: Z = 53000
P12211: Z = 46000

37. p12221
X1 1 X3 0.74 X5 1
X2 1 X4 0 X6 0
Z=51542.86
p12222
X1 X3 X5
X2 X4 X6
INFACTIBLE
X6 = 0 X6 = 1
RAMIFICANDO POR 1222
p1222
X1 1 X3 0 X5 1
X2 1 X4 0 X6 0.8
Z=53400
P11: Z = 49500
P211: Z = 48000
P2211: Z = 49500
P121: Z = 52500
P2121: Z = 53000
P12211: Z = 46000
TERMINAMOS!!!

38. p21
21
VISTA DE LA RAMIFICACIÓN

39. Finalizando el proceso de ramificación y poda, para el problema
de tipo PLB.
La solución óptima entera corresponde al sub problema P2121
Max Z = 15000x1+10000x2+11500x3+25000x4+18000x5+13000x6
SUJETO A:
10100x1+6000x2+7000x3+18000x4+13700x5+6500x6 <= 35000
X1 + X2 + X3 >= 1
x4 + x5 <=1
DONDE: X1=1, X2=0, X3=0, X4=1, X5=0, X6=1
La solución óptima es:
Desarrollar los proyectos:
• Configurador I
• Web App Sunat
• Web Services Sunat
Obteniendo un ingreso de 53000 soles.

40. MÉTODOS DE PLANOS DE CORTE O ALGORITMO DE
GOMORY
Un método para resolver problemas de Programación Lineal Entera Mixta y Pura es el
procedimiento del Plano Cortante de Gomory.
Este procedimiento que produce la mejor solución cuando las variables deben ser expresadas
en números enteros; inicia resolviendo el problema por el método Simplex sin considerar el
requerimiento de enteros.
Después de que la solución óptima no entera es obtenida a través del Simplex, una nueva
restricción Lineal es desarrollada para satisfacer los requerimientos de enteros.
La nueva ecuación restrictiva es añadida a la tabla del Simplex y una nueva variable entra en
solución. Cuando la nueva variable entra en solución, causa que al menos una de las variables
básicas tome un valor entero. El proceso continuo hasta que todas las variables básicas sean
enteras.

41. ALGORITMO FRACCIONAL DE GOMORY
• Paso 1: Obtenga la solución optima usando el método simplex
• Paso 2: ¿Si son todas las variables básicas enteras? Pase al último paso, lo
contrario continúe con el paso 3.
• Paso 3: Seleccione la restricción con la mayor parte fraccional en su
solución
• Paso 4: De tal selección se separan la parte entera, es decir, quedarse
solamente con la parte fraccionaria.
• Paso 5: Y de ello tendremos únicamente a las variables de holgura sin
multiplicar por (-1) ,siendo esta ecuación menor igual a “0”.(ecuación 1)
• Paso 6: Se toman las restricciones al inicio del problema estandarizadas, a
continuación deberá de despejar las variables no básicas, con el objetivo de
tener ecuaciones en función a las variables básicas.

42. ALGORITMO FRACCIONAL DE GOMORY
• Paso 7: Deberá de reemplazar estas variables en la ecuación
anterior (ecuación 1), teniendo una nueva restricción en función a
las variables básicas.
• Paso 8: Ahora se tendrá un nuevo problema agregando la nueva
restricción, aplicando el método simplex.
• Paso 9: Si son todas las variables básicas enteras, vaya al último
paso, caso contrario, vaya al paso 3.
 Paso 10: Se ha obtenido la solución óptima entera

43. Algoritmo Fraccional de Gomory
Ejemplo:
Función Objetivo: Maximizar Z = 7x1 + 10x2
S. a:
-x1 + 3x2 ≤ 6
7x1 + x2 ≤ 35
Criterio de no negatividad: x1, x2 ≥ 0 y entero
Estandarizando:
Maximizar Z = 7x1 + 10x2 + 0x3 + 0x4
Sujeto a:
-x1 + 3x2 + x3 = 6
7x1 + x2 + x4 = 35
x1, x2, x3, x4 ≥ 0 y entero

44. Algoritmo Fraccional de Gomory
Cj 7 10 0 0
Ck Xk bi X1 X2 X3 X4 b
0
0
X3
X4
6
35
-1
7
3
1
1
0
0
1
2
35
Zj 0 0 0 0 0
Zj- Cj -7 -10 0 0
Cj 7 10 0 0
Ck Xk bi X1 X2 X3 X4 b
10
0
X2
X4
2
33
-1/3
22/3
1
0
1/3
-1/3
0
1
-6
99/2
Zj 20 -10/3 10 10/3 0
Zj- Cj -31/3 0 -10/3 0
PRIMERA TABLA SIMPLEX
Elemento Pivote
SEGUNDA TABLA SIMPLEX
Elemento Pivote

45. Algoritmo Fraccional de Gomory
TERCERA TABLA SIMPLEX
Cj 7 10 0 0
Ck Xk bi X1 X2 X3 X4
10
7
X2
X1
7/2
9/2
0
1
1
0
7/22
-1/22
1/22
3/22
Zj 133/2 7 10 63/22 31/22
Zj- Cj 0 0 63/22 31/22
La solución óptima es: X1 = 9 / 2
X2 = 7 / 2
X3 = 0
X4 = 0
Z = 133 / 2

46. En la primera iteración del algoritmo del plano de corte se puede usar cualquiera de los cortes .
Cálculo de la nueva restricción, a partir de la Ecuación 1
X2 + 7/22 X3 + 1/22 X4 = 7/2
Remplazamos cada coeficiente de la ecuación, por la suma de un número entero de cualquier
signo y una fracción no negativa menor que uno (1).
(1+0)X2 + (0+7/22)X3 + (0+1/22)X4 = (3+1/2)
Trasladamos los términos con coeficiente entero, al lado izquierdo.
X2 - 3 = 1/2 - 7/22X3 - 1/22X4
Ecuación X2: X2 + 7/22 X3 + 1/22 X4 = 7/2
Ecuación X1: X1 – 1/22 X3 + 3/22 X4 = 9/2
Fraccionaria
Entera
Información de la tabla Simplex Óptima

47. Tomamos la parte fraccional, en la cual tiene q ser (<=0)
1/2 - 7/22X3 - 1/22X4 <= 0
-7/22X3 - 1/22X4 <= -1/2
Adicionando una variable de holgura (s1)
-7/22X3 - 1/22X4 + s1= -1/2 , s1=>0 ………………………CORTE I
Esta restricción se añade como una restricción secundaria a la tabla simplex óptima.
Cj 7 10 0 0 0
Ck Xk bi X1 X2 X3 X4 S1
10
7
0
X2
X1
S1
7/2
9/2
-1/2
0
1
0
1
0
0
7/22
-1/22
-7/22
1/22
3/22
-1/22
0
0
1
Zj 133/2 7 10 63/22 31/22 0
Zj- Cj 0 0 63/22 31/22 0
La tabla símplex es óptima, pero no factible. Aplicamos el método simplex dual para recuperar la
factibilidad, lo que nos da:

48. Cj 7 10 0 0 0
Ck Xk Bi X1 X2 X3 X4 S1
10
7
0
X2
X1
X3
3
32/7
11/7
0
1
0
1
0
0
0
0
1
0
1/7
1/7
1
-1/7
-22/7
Zj 62 7 10 0 1 9
Zj- Cj 0 0 0 1 9
Restricción para el segundo corte
TABLA SIMPLEX (RESULTADO DEL PRIMER CORTE)

49. Algoritmo Fraccional de Gomory
La última solución todavía es de no enteros en X1 Y X3.
Entonces seleccionamos X1 como el renglón fuente
X1 + 1/7 X4 – 1/7 S1 = 32/7
X1 + (0 + 1/7) X4 – (-1 + 6/7) S1 = (4 + 4/7)
El corte asociado es:
-1/7 X4 – 6/7 S1 + 4/7 ≤ 0
-1/7 X4 – 6/7 S1 ≤ -4/7
-1/7 X4 – 6/7 S1 + S2 = -4/7 , s2=>0 .............(CORTE II)
X2 = 3
X1 = 32/7
X3 = 11/7
Z = 62
Solución obtenida:
Ahora agregamos la nueva restricción a nuestra última tabla simplex dual.

50. Cj 7 10 0 0 0 0
Ck Xk Bi X1 X2 X3 X4 S1 S2 d
10
7
0
0
X2
X1
X3
S2
3
32/7
11/7
-4/7
0
1
0
0
1
0
0
0
0
0
1
0
0
1/7
1/7
-1/7
1
-1/7
-22/7
-6/7
0
0
0
1
3
-32
-½
2/3
Zj 62 7 10 0 1 9 0
Zj-Cj 0 0 0 1 9 0
(Zj-Cj)/arj - - - -7 -63/7 -
Elemento pivote
El menos
negativo
Algoritmo Fraccional de Gomory
PRIMERA TABLA SIMPLEX DUAL

51. Algoritmo Fraccional de
Gomory
Cj 7 10 0 0 0 0
Ck Xk bi X1 X2 X3 X4 S1 S2
10
7
0
0
X2
X1
X3
X4
3
4
1
4
0
1
0
0
1
0
0
0
0
0
1
0
0
0
0
1
1
-1
-4
6
0
1
1
-7
Zj 58 7 10 0 0 3 7
Zj-Cj 0 0 0 0 3 -7
ULTIMA TABLA SIMPLEX(RESULTADO DEL SEGUNDO CORTE)

52. Algoritmo Fraccional de Gomory
X2=3
X1=4
X3=1
X4=4
S1=0
S2=0
La Solución Optima Entera es Cuando:
Z=58

53. 23X1 + 32X2 ≥120
15X1 + 29X2 ≥ 50
x1, x2 ≥ 0 y entero
Las restricciones:
La función Objetivo:
ZMIN = 35X1 + 48X2
EJERCICIO 02

54. Paso 1: Dualizamos el problema
ZMAX = 120X1 + 50X2
s.a.
23X1 + 15X2 ≤ 35
32X1 + 29X2 ≤ 48
Paso 2: Convertir las inecuaciones en ecuaciones
23X1 + 15X2 + 1X3 + 0X4 = 35
32X1 + 29X2 + 0X3 + 1X4 = 48

55. Paso 3: Resolvemos el problema mediante el método simplex
Cj 120 50 0 0
Ck Xk Bi X1 X2 X3 X4
0
120
X3
X1
1/2
48/32
0
1
-5.84
0.91
1
0
-0.72
0.03
Zj 180 120 108.75 0 3.75
Zj- Cj 0 58.75 0 3.75

56. Paso 4: Obtenemos la fila de la variable que queremos convertir
X1 + 0.91X2 + 0X3 + 0.03X4 = 48/32
Paso 6: Separamos los enteros de los fraccionarios o decimales
X1 - 1 = - 0.91X2 - 0.03X4 + 0.5
Paso 5: Convertimos las fracciones mayores que 1 en menores que 1
X1 + 0.91X2 + 0.03X4 = 1 + 0.5

57. Paso 7: Tomamos la parte fraccional, en la cual tiene que ser (≤ 0)
- 0.91X2 - 0.03X4 + 0.5 ≤ 0
- 0.91X2 - 0.03X4 ≤ - 0.5
Paso 8: Agregamos una variable de holgura
- 0.91X2 - 0.03X4 + X5 ≤ - 0.5

58. Cj 120 50 0 0 0
Ck Xk Bi X1 X2 X3 X4 X5
0
120
0
X3
X1
X5
1/2
48/32
-0.5
0
1
0
-5.84
0.91
-0.91
1
0
0
-0.72
0.03
-0.03
0
0
1
Zj 180 120 108.75 0 3.75
Zj- Cj 0 58.75 0 3.75
Paso 9: Agregamos la ecuación en el simplex y resolvemos

59. Cj 120 50 0 0 0
Ck Xk Bi X1 X2 X3 X4 X5
0
120
50
X3
X1
X2
675/182
1
50/91
0
1
0
0
0
1
1
0
0
-48/91
0
3/91
-584/91
0
-100/91
Zj 13420/91 120 50 0 150/91 -5000/91
Zj- Cj 0 0 0 150/91 -5000/91
Paso 10: Si las variables reales son enteras acaba el problema, sino
aplicamos de nuevo gomory (paso 4)

60. X2 + (3/91)X4 – (100/91)X5 = 50/91
X2 + (3/91)X4 - 2+ (82/91)X5 = 50/91
X2 – 2 = -(3/91) X4 – (82/91) X5 + (50/91)
-(3/91) X4 – (82/91) X5 + X6 ≤ -(50/91)

61. Cj 120 50 0 0 0 0
Ck Xk Bi X1 X2 X3 X4 X5 X6
0
120
50
0
X3
X1
X2
X6
675/182
1
50/91
-50/91
0
1
0
0
0
0
1
0
1
0
0
0
-48/91
0
3/91
-3/91
-584/91
0
-100/91
-82/91
0
0
0
1
Zj 13420/91 120 50 0 150/91 -5000/91 0
Zj- Cj 0 0 0 150/91 -5000/91 0

62. Cj 120 50 0 0 0 0
Ck Xk Bi X1 X2 X3 X4 X5 X6
0
120
50
0
X3
X1
X2
X4
75/2275
1
0
50/3
0
1
0
0
0
0
1
0
1
0
0
0
0
0
0
1
1312/91
0
-82/91
82/3
-2040/91
0
1
-91/3
Zj 120 120 50 0 0 -4000/91 50
Zj- Cj 0 0 0 0 -4000/91 50
X1 = 1 X2 = 0 Z = 120

63.  Consiste en enumerar todas las soluciones posibles, a partir de los
valores tomados para las variables enteras y realizar todas las
combinaciones posibles hasta encontrar una combinación que nos
proporcione el valor óptimo de la función objetivo y que cumpla con
todas las restricciones del problema.
Es el número de variables, ya que se presentan demasiadas
combinaciones antes de encontrar la solución óptima.
Método de Enumeración Exhaustiva o
Explicita
Principal Desventaja:

64.  Una empresa esta estudiando la posibilidad de expansión mediante la
construcción de una nueva fábrica ya sea en la Ciudad 1 o en la Ciudad 2 o
en ambas ciudades. Si se construye una fábrica en la ciudad X, se puede
construir un almacén en dicha ciudad, pero solo se construiría uno. La
siguiente tabla muestra el beneficio aportado por la inversión y costes.
Sabiendo que el capital total disponible es de 10.
Decisión ¿Sí o No? Beneficio Coste
1 Fábrica en la Ciudad 1 9 6
2 Fábrica en la Ciudad 2 5 3
3 Almacén en la Ciudad 1 6 5
4 Almacén en la Ciudad 2 4 2
 Se pide encontrar la solución que maximiza el beneficio total
Ejemplos: Problema “PEB”

65. 1.Variables de Decisión: 𝑋1, 𝑋2, 𝑋3, 𝑋4
𝑋1: Construir fábrica en ciudad 1
𝑋2: Construir fábrica en ciudad 2
𝑋3: Construir almacén en ciudad 1
𝑋4: Construir almacén en ciudad 2
Variables Binarias(0 o 1)
𝑋𝑖 = 1 → Afirmación
𝑋𝑖 = 0 → Negación
2.Función Objetiva:
Max Z = 9𝑋1 + 5𝑋2 + 6𝑋3+ 4𝑋4
3.Sujeto a: 6𝑋1 + 3𝑋2 + 5𝑋3+ 2𝑋4 ≤ 10
𝑋3 ≤ 𝑋1
𝑋4 ≤ 𝑋2
𝑋3 + 𝑋4 ≤ 1
4.Criterio de No-Negatividad :
𝑋1, 𝑋2, 𝑋3, 𝑋4 ∈ {0,1}
Ejemplos: Problema “PEB”
Solución

66.  Hallando posibles soluciones:
2𝑛
24
= 16
Casos Fab1 Fab2 Alm1 Alm2 Beneficio Coste Si/No
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
NO SI SI SI
SI SI SI SI
SI SI SI NO
SI SI NO SI
SI NO SI SI
SI SI NO NO
SI NO SI NO
NO SI SI NO
SI NO NO SI
NO SI NO SI
NO NO SI SI
SI NO NO NO
NO SI NO NO
NO NO SI NO
NO NO NO SI
NO NO NO NO

67. Casos Fab1 Fab2 Alm1 Alm2 Beneficio Coste Si/No
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
NO SI SI SI
SI SI SI SI
SI SI SI NO
SI SI NO SI
SI NO SI SI
SI SI NO NO
SI NO SI NO
NO SI SI NO
SI NO NO SI
NO SI NO SI
NO NO SI SI
SI NO NO NO
NO SI NO NO
NO NO SI NO
NO NO NO SI
NO NO NO NO
Decisión ¿Sí o No? Beneficio Coste
1 Fábrica en la
Ciudad 1
9 6
2 Fábrica en la
Ciudad 2
5 3
3 Almacén en
la Ciudad 1
6 5
4 Almacén en
la Ciudad 2
4 2
20
18
---
---
14
---
---
---
15
---
9
9
---
---
5
0
14
11
---
---
9
---
---
---
11
---
6
5
---
---
3
0

68. Casos Fab1 Fab2 Alm1 Alm2 Beneficio Coste Si/No
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
NO SI SI SI
SI SI SI SI
SI SI SI NO
SI SI NO SI
SI NO SI SI
SI SI NO NO
SI NO SI NO
NO SI SI NO
SI NO NO SI
NO SI NO SI
NO NO SI SI
SI NO NO NO
NO SI NO NO
NO NO SI NO
NO NO NO SI
NO NO NO NO
20
18
---
---
14
---
---
---
15
---
9
9
---
---
5
0
14
11
---
---
9
---
---
---
11
---
6
5
---
---
3
0
NO
NO
---
---
SI
---
---
---
NO
---
SI
SI
---
---
SI
SI
Decisión ¿Sí o No? Beneficio Coste
1 Fábrica en la
Ciudad 1
9 6
2 Fábrica en la
Ciudad 2
5 3
3 Almacén en
la Ciudad 1
6 5
4 Almacén en
la Ciudad 2
4 2

69. Casos Fab1 Fab2 Alm1 Alm2 Beneficio Coste Si/No
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
NO SI SI SI
SI SI SI SI
SI SI SI NO
SI SI NO SI
SI NO SI SI
SI SI NO NO
SI NO SI NO
NO SI SI NO
SI NO NO SI
NO SI NO SI
NO NO SI SI
SI NO NO NO
NO SI NO NO
NO NO SI NO
NO NO NO SI
NO NO NO NO
20
18
---
---
14
---
---
---
15
---
9
9
---
---
5
0
14
11
---
---
9
---
---
---
11
---
6
5
---
---
3
0
NO
NO
---
---
SI
---
---
---
NO
---
SI
SI
---
---
SI
SI
Decisión ¿Sí o No? Beneficio Coste
1 Fábrica en la
Ciudad 1
9 6
2 Fábrica en la
Ciudad 2
5 3
3 Almacén en la
Ciudad 1
6 5
4 Almacén en la
Ciudad 2
4 2

70. Casos Fab1 Fab2 Alm1 Alm2 Beneficio Coste Si/No
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
NO SI SI SI
SI SI SI SI
SI SI SI NO
SI SI NO SI
SI NO SI SI
SI SI NO NO
SI NO SI NO
NO SI SI NO
SI NO NO SI
NO SI NO SI
NO NO SI SI
SI NO NO NO
NO SI NO NO
NO NO SI NO
NO NO NO SI
NO NO NO NO
20
18
---
---
14
---
---
---
15
---
9
9
---
---
5
0
14
11
---
---
9
---
---
---
11
---
6
5
---
---
3
0
NO
NO
---
---
SI
---
---
---
NO
---
SI
SI
---
---
SI
SI
DONDE:
𝑋1 = 1
𝑋2 = 1
𝑋3 = 0
𝑋4 = 0
Max Z = 9𝑋1 + 5𝑋2 + 6𝑋3+ 4𝑋4
Max Z = 14

71. 1. Función Objetiva:
MAX Z = 3𝑋1 + 5𝑋2
2. Sujeta a :
a) 𝑋1 + 𝑋2 ≤ 8
b) 3𝑋1 + 2𝑋2 ≤ 7
3. Criterio de No-Negatividad:
𝑋𝑖 ≥ 0 𝑖 = 1,2
A. Hallando posibles valores de 𝑋1
B. Hallando posibles valores de 𝑋2
A.1. Según la restricción “a”
𝑋1 = 0,1,2,3,4,5,6,7,8
A.2. Según la restricción “b”
𝑋1 = 0,1,2
𝐸𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑋1 = 0,1,2
B.1. Según la restricción “a”
𝑋2 = 0,1,2,3,4,5,6,7,8
B.2. Según la restricción “b”
𝑋1 = 0,1,2,3
𝐸𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑋2 = 0,1,2,3
Ejemplos: Problema “PEB”
Solución

72. C. Hallando posibles soluciones aplicando los valores 𝑋1 y 𝑋2
𝑿𝟏 𝑿𝟐 𝑹𝟏 𝑹𝟐 Z Admisible
𝐒𝟏 0 0
𝐒𝟐 0 1
𝐒𝟑 0 2
𝐒𝟒 0 3
𝐒𝟓 1 0
𝐒𝟔 1 1
𝐒𝟕 1 2
𝐒𝟖 1 3
𝐒𝟗 2 0
𝐒𝟏𝟎 2 1
𝐒𝟏𝟏 2 2
𝐒𝟏𝟐 2 3
Ejemplos: Problema “PEB”

73. C. Hallando posibles soluciones aplicando los valores 𝑋1 y 𝑋2
𝑿𝟏 𝑿𝟐 𝑹𝟏 𝑹𝟐 Z Admisible
𝐒𝟏 0 0 0
𝐒𝟐 0 1 1
𝐒𝟑 0 2 2
𝐒𝟒 0 3 3
𝐒𝟓 1 0 1
𝐒𝟔 1 1 2
𝐒𝟕 1 2 3
𝐒𝟖 1 3 4
𝐒𝟗 2 0 2
𝐒𝟏𝟎 2 1 3
𝐒𝟏𝟏 2 2 4
𝐒𝟏𝟐 2 3 5
Ejemplos: Problema “PEB”

74. C. Hallando posibles soluciones aplicando los valores 𝑋1 y 𝑋2
𝑿𝟏 𝑿𝟐 𝑹𝟏 𝑹𝟐 Z Admisible
𝐒𝟏 0 0 0 0
𝐒𝟐 0 1 1 2
𝐒𝟑 0 2 2 4
𝐒𝟒 0 3 3 6
𝐒𝟓 1 0 1 3
𝐒𝟔 1 1 2 5
𝐒𝟕 1 2 3 7
𝐒𝟖 1 3 4 9
𝐒𝟗 2 0 2 6
𝐒𝟏𝟎 2 1 3 8
𝐒𝟏𝟏 2 2 4 10
𝐒𝟏𝟐 2 3 5 12
Ejemplos: Problema “PEB”

75. C. Hallando posibles soluciones aplicando los valores 𝑋1 y 𝑋2
𝑿𝟏 𝑿𝟐 𝑹𝟏 𝑹𝟐 Z Admisible
𝐒𝟏 0 0 0 0 0
𝐒𝟐 0 1 1 2 5
𝐒𝟑 0 2 2 4 10
𝐒𝟒 0 3 3 6 15
𝐒𝟓 1 0 1 3 3
𝐒𝟔 1 1 2 5 8
𝐒𝟕 1 2 3 7 13
𝐒𝟖 1 3 4 9 18
𝐒𝟗 2 0 2 6 6
𝐒𝟏𝟎 2 1 3 8 11
𝐒𝟏𝟏 2 2 4 10 16
𝐒𝟏𝟐 2 3 5 12 21
Ejemplos: Problema “PEB”

76. C. Hallando posibles soluciones aplicando los valores 𝑋1 y 𝑋2
𝑿𝟏 𝑿𝟐 𝑹𝟏 𝑹𝟐 Z Admisible
𝐒𝟏 0 0 0 0 0
𝐒𝟐 0 1 1 2 5
𝐒𝟑 0 2 2 4 10
𝐒𝟒 0 3 3 6 15
𝐒𝟓 1 0 1 3 3
𝐒𝟔 1 1 2 5 8
𝐒𝟕 1 2 3 7 13
𝐒𝟖 1 3 4 9 18
𝐒𝟗 2 0 2 6 6
𝐒𝟏𝟎 2 1 3 8 11
𝐒𝟏𝟏 2 2 4 10 16
𝐒𝟏𝟐 2 3 5 12 21
Ejemplos: Problema “PEB”

77. C. Hallando posibles soluciones aplicando los valores 𝑋1 y 𝑋2
𝑿𝟏 𝑿𝟐 𝑹𝟏 𝑹𝟐 Z Admisible
𝐒𝟏 0 0 0 0 0 SI
𝐒𝟐 0 1 1 2 5 SI
𝐒𝟑 0 2 2 4 10 SI
𝐒𝟒 0 3 3 6 15 SI
𝐒𝟓 1 0 1 3 3 SI
𝐒𝟔 1 1 2 5 8 SI
𝐒𝟕 1 2 3 7 13 SI
𝐒𝟖 1 3 4 9 18 NO
𝐒𝟗 2 0 2 6 6 SI
𝐒𝟏𝟎 2 1 3 8 11 NO
𝐒𝟏𝟏 2 2 4 10 16 NO
𝐒𝟏𝟐 2 3 5 12 21 NO
Ejemplos: Problema “PEB”

78. C. Hallando posibles soluciones aplicando los valores 𝑋1 y 𝑋2
𝑿𝟏 𝑿𝟐 𝑹𝟏 𝑹𝟐 Z Admisible
𝐒𝟏 0 0 0 0 0 SI
𝐒𝟐 0 1 1 2 5 SI
𝐒𝟑 0 2 2 4 10 SI
𝐒𝟒 0 3 3 6 15 SI
𝐒𝟓 1 0 1 3 3 SI
𝐒𝟔 1 1 2 5 8 SI
𝐒𝟕 1 2 3 7 13 SI
𝐒𝟖 1 3 4 9 18 NO
𝐒𝟗 2 0 2 6 6 SI
𝐒𝟏𝟎 2 1 3 8 11 NO
𝐒𝟏𝟏 2 2 4 10 16 NO
𝐒𝟏𝟐 2 3 5 12 21 NO
Ejemplos: Problema “PEB”

79. C. Hallando posibles soluciones aplicando los valores 𝑋1 y 𝑋2
𝑿𝟏 𝑿𝟐 𝑹𝟏 𝑹𝟐 Z Admisible
𝐒𝟏 0 0 0 0 0 SI
𝐒𝟐 0 1 1 2 5 SI
𝐒𝟑 0 2 2 4 10 SI
𝐒𝟒 0 3 3 6 15 SI
𝐒𝟓 1 0 1 3 3 SI
𝐒𝟔 1 1 2 5 8 SI
𝐒𝟕 1 2 3 7 13 SI
𝐒𝟖 1 3 4 9 18 NO
𝐒𝟗 2 0 2 6 6 SI
𝐒𝟏𝟎 2 1 3 8 11 NO
𝐒𝟏𝟏 2 2 4 10 16 NO
𝐒𝟏𝟐 2 3 5 12 21 NO
Ejemplos: Problema “PEB”

80. D. Concluyendo:
MAX Z = 3𝑿𝟏 + 5𝑿𝟐
Donde:
𝑿𝟏 = 𝟎
𝑿𝟐 = 𝟑
Z = 15
Ejemplos: Problema “PEB”