Protecciones eléctricas

1. MODULO PROTECCIONES ELECTRICAS

2. CONTENIDO
Fundamentos de prácticas de protección
• Introducción
• Necesidad de un sistema de protecciones
• Características de los sistemas de protección
• Zonas de protección
• Protección principal y de respaldo
• Símbolos de equipos y dispositivos según normas ANSI/IEC
Cálculos de fallas
• Fallas trifásicas
• Análisis de redes de secuencia
• Ecuaciones y conexiones de redes de secuencia para diferentes
fallas
• Parámetros y circuitos equivalentes
• Distribución de corrientes en un sistema debido a una falla

3. CONTENIDO
Análisis de redes de secuencia
Componentes de un sistema de protecciones
•Transformadores de corriente y de voltaje
Tecnologías de relés
• Relés electromecánicos, estáticos, digitales y numéricos
Protección de sobrecorriente
• Procedimientos de coordinación
• Principios de coordinación corriente/tiempo
• Relés de sobrecorriente de tiempo inverso
• Relés temporizados e instantáneos
• Relés de sobrecorriente de tiempo definido
• Criterios de ajustes y coordinación para relés de sobrecorriente

4. CONTENIDO
Protección de sobrecorriente direccional
• Principios básicos
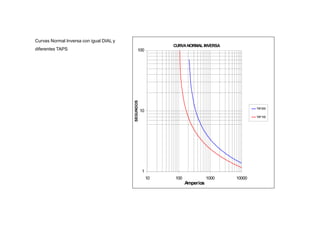
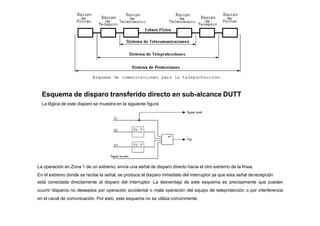
• Representación de las características de una protección
direccional
• Polarización de relés direccionales
• Aplicación de relés direccionales
Protección de distancia
• Generalidades
• Diagramas R-X
• Características de los relés de distancia
• Criterios de ajustes, ejemplos de aplicación.
• Esquemas de protección de distancia

5. CONTENIDO
Protección diferencial
• Protección diferencial de barras
• Protección diferencial tipo porcentual
• Protección diferencial de alta impedancia
• Protección diferencial de transformador
Recierre
• Aplicaciones
• Características de operación

6. FUNDAMENTOS DE PRACTICAS DE PROTECCION
Introducción
El desarrollo del proyecto de un Sistema Eléctrico de Potencia, así como el estudio racional de sus normas de
operación, debe consultar, básicamente, dos aspectos principales: operación en condiciones normales y
operación en condiciones anormales.
La operación en condiciones normales supone que el sistema cumple con los requisitos necesarios para servir
la demanda del consumo de acuerdo a una cierta calidad prefijada del servicio suministrado.
Así, por ejemplo, el sistema deberá poseer la capacidad de reserva necesaria para poder abastecer los
aumentos del consumo; mantendrá los niveles de voltaje dentro de rangos adecuados; regulará la frecuencia;
las cargas se repartirán entre las diferentes centrales generadoras conforme a la distribución más económica;
se mantendrá en forma adecuada; etc.
La operación normal de un sistema no considera la ocurrencia de fallas en el equipo, ni la presencia de
fenómenos incontrolables como tormentas y descargas atmosféricas, o los errores cometidos por los
operadores.

7. Cuando el sistema está bajo el efecto de uno de estos factores se dice que está operando bajo condiciones
anormales y en este caso pueden ocurrir dos fenómenos de importancia:
−El equipo o parte del sistema, puede sufrir daños de consideración si la intensidad y la duración de la
perturbación exceden magnitudes determinadas.
− La calidad del servicio suministrado se resiente gravemente.
Frente al problema de operación anormal, el proyectista de un sistema eléctrico de potencia puede adoptar dos
puntos de vista:
− Incorporar al diseño ciertas características que eliminen la posibilidad de fallas.
−Permitir la ocurrencia de las fallas incluyendo en el proyecto características y elementos que reduzcan
el daño causado por las mismas.

8. La primera solución es prácticamente imposible o por lo menos, no justificable económicamente. En la mayoría
de los casos, se sigue el criterio de permitir la ocurrencia de ciertas fallas y tratar de aminorar sus efectos tanto
en el equipo instalado como en la calidad del servicio suministrado. Un diseño moderno consulta ambas
soluciones en la proporción que los estudios económicos aconsejen.
Los sistemas de protecciones eléctricas constituyen el equipo más importante que se incluye en un sistema
eléctrico de potencia con el fin de alcanzar el último objetivo, esto es, aminorar los efectos de las fallas sobre el
equipo protegido desenergizándolo rápidamente y mejorar la calidad del servicio al eliminar o aislar aquellos
elementos que por su operación defectuosa puedan producir perturbaciones.
Con el notable crecimiento de los sistemas eléctricos en los últimos años, el aumento de interconexión, el alto
costo del equipo instalado y las exigencias cada vez mayores de un suministro de energía eléctrica seguro y de
óptima calidad, la técnica de las protecciones eléctricas ha debido necesariamente perfeccionarse en forma
paralela, pues, como ya se ha dicho, son ellas, en gran parte, las responsables de esas características
deseables. Por esto, un diseño cuidadoso del sistema de protecciones y la elección adecuada de sus
componentes es considerado, hoy en día, de una importancia fundamental en la operación de los sistemas
eléctricos.

9. Necesidad de un sistema de protecciones eléctricas
Las protecciones eléctricas son los dispositivos que tienen como principal finalidad la de detectar condiciones
anormales en la operación de un Sistema Eléctrico de Potencia y tomar en forma automática las medidas que
se requieran para restablecer la operación normal.
En el caso de fallas en equipos eléctricos, la medida será retirarlos del servicio y, en el caso de fallas en un
sistema eléctrico, será necesario aislar el sector que produce la anormalidad. Durante la operación normal de
los sistemas eléctricos, las acciones están entregadas al hombre o a equipos automáticos que desempeñan su
función dentro de límites determinados, en cambio, las protecciones no son requeridas en condiciones
normales pero deben estar disponibles inmediatamente para manejar condiciones intolerables para el sistema y
evitar daños mayores o paralizaciones no deseadas.

10. Características de los sistemas de protección
Las características de un sistema de protecciones se analizan principalmente bajo el punto de vista de su
operación en condiciones de anormalidad, siendo las principales las que se indican a continuación.
Confiabilidad o seguridad
Es la característica que permite garantizar la operación de las protecciones, cada vez que se produzca una
falla. Complementando esta definición se puede agregar que es la característica del relé o del sistema de
protecciones que le permite actuar correctamente cuando es requerido y evitar operaciones innecesarias.
Cuando se presenta la anormalidad, las protecciones deben estar en condiciones de operar correctamente. En
algunos casos, es posible que ciertos equipos sean requeridos muy pocas veces durante su vida útil, pero aún
en estas condiciones deberán operar en forma correcta. Para lograr esta cualidad se debe recurrir a diseños
simples, con componentes robustos y de buena calidad, que sean periódicamente sometidos a mantención
para comprobar que se encuentran bien calibrados, bien conectados y que la orden que emitan sea cumplida
por los sistemas de control.

11. Selectividad
Es la cualidad de las protecciones que les permite discriminar la ubicación de la falla, con el objeto de aislar
exclusivamente el equipo fallado, manteniendo en servicio lo que no sea imprescindible desconectar. De este
modo se obtiene la máxima continuidad del servicio con un mínimo de desconexiones.
Rapidez
Es conveniente que las protecciones operen en el mínimo tiempo posible, disminuyendo con ello la duración de
la falla, las perturbaciones al resto el sistema y los consecuentes daños a los equipos. La rapidez redunda
también en una mayor efectividad de las reconexiones automáticas y mejora la estabilidad del sistema. Aunque
es deseable la operación instantánea de las protecciones, muchas veces esta cualidad debe sacrificarse con el
objeto de mejorar otros aspectos, tales como la selectividad. La temporización en todo caso debe ser
compatible con los límites de resistencia de los equipos a las fallas consideradas y su empleo para obtener
selectividad está asociado a otra característica que siempre debe considerarse, como es la economía.

12. Exactitud
Las protecciones deben operar con la mínima desviación respecto de la magnitud teórica de ajuste. La
exactitud, se expresa como un error de medida, es decir, como la razón entre el valor de operación y el valor
teórico de ajuste. Las desviaciones máximas aceptadas varían entre un 5 y un 10%, según el caso.
Sensibilidad
El sistema de protecciones y sus elementos asociados debe ser capaz de operar detectando la falla de mínimo
nivel que ocurra dentro de su zona de operación o la menor variación de la magnitud que controla respecto de
la magnitud de referencia o ajuste. Esto no siempre es posible en la práctica. Por ejemplo, en períodos de
sequía o en la época de verano, cuando cae una fase a tierra (pavimento) se producen fallas de muy baja
corriente, las que pueden no ser detectadas por las protecciones.
Puesto que no es posible satisfacer plenamente cada uno de estos requerimientos en forma simultánea, deben
adoptarse algunas soluciones de compromiso. En general se otorga mayor atención a aquellos problemas que
de acuerdo a la experiencia es posible que ocurran. De aquí que se diga que el tema de las protecciones tiene
mucho de técnica pero es también un arte. De hecho, diferentes especialistas utilizando una lógica razonable
pueden llegar a soluciones significativamente diferentes para un mismo problema.

13. Zonas de operación
Las protecciones del sistema de potencia abarcan ciertas zonas de operación según su tipo. Es conveniente
que entre las zonas de operación de dos protecciones contiguas no queden sectores sin cubrir por alguna de
ellas. Para este efecto se deben superponer los bordes de las zonas contiguas y por lo tanto, no se acepta que
sean tangentes. La figura siguiente muestra el Diagrama Unilineal de un sistema, indicando las zonas de
protección.
1 Generador o unidad generador-transformador
2 Transformadores
3 Barra de subestaciones
4Líneas de transmisión o distribución
5 Motores

14. Protección de respaldo
Si al producirse una anormalidad en el sistema de potencia, la protección encargada de aislar la zona (llamada
protección principal) no opera, los daños a los equipos serían mayores y la falla se propagaría por el resto del
sistema con las consecuencias previsibles.
Para que esto no ocurra se utiliza el respaldo, es decir, otra protección deberá ser capaz de detectar la falla y
aislarla, aún a costa de dejar fuera de servicio equipos o sectores en condiciones normales. Donde más se
aplica esta técnica, por razones económicas es en el caso de los cortocircuitos. Según la ubicación de la
protección que da respaldo, este puede ser local o remoto.
Respaldo Local
Se ubica en la zona protegida y puede ser del tipo duplicación de la protección completa o parte de ella. Puede
ser también del tipo adicional, tal como un relé de tiempo por ejemplo.
Respaldo Remoto
Este tipo de respaldo lo proporciona una protección ubicada en otro punto del sistema de potencia. Por lo
general, esta protección es del tipo principal en su zona de operación.

15. Símbolos de equipos y dispositivos según normas ANSI/IEC
Existen dos métodos para indicar las funciones de los relés de protección:
Uno es dado por la norma ANSI C37-2 y utiliza un sistema de números para cada función. Las funciones se
complementan con letras donde se requiere una ampliación de la función.
El otro es dado por la norma IEC 60617 y utiliza símbolos gráficos.

17. CALCULOS DE FALLAS
Introducción
Un sistema de potencia es tratado normalmente como una red trifásica simétricamente balanceada. Cuando
ocurre una falla normalmente se pierde la simetría, por lo que resulta en la aparición de corrientes y tensiones
desbalanceadas.
La única excepción es la falla trifásica, la cual debido a que involucra las tres fases en forma igual en la misma
ubicación, se describe como una falla balanceada.
Es posible analizar estas condiciones de falla utilizando un análisis de componentes simétricas y reemplazando
las fuentes del sistema por una fuente en el lugar de la falla.
Para la correcta aplicación de los equipos de protección, es esencial conocer la distribución de la corriente de
falla a través de todo el sistema y los voltajes en diferentes partes del sistema debido a una falla.
Adicionalmente, se deben conocer los valores límites de corriente en cualquier ubicación de relés si se requiere
despejar la falla con discriminación.

18. La información que normalmente se requiere para cada falla en cada ubicación de relé es la siguiente:
•Corriente de falla máxima
•Corriente de falla mínima
•Distribución de corriente de aporte
En general las corrientes de cortocircuito alcanzan magnitudes mucho mayores que los valores nominales de
los generadores, transformadores y líneas. Si se permite que estas corrientes circulen por un período
prolongado, pueden causar un serio daño térmico al equipo y problemas de estabilidad de funcionamiento en el
sistema de potencia.
En este aspecto, el tipo de cortocircuito más severo es el trifásico, el que además de dar valores elevados de
corriente, reduce a cero la capacidad de transmisión de una línea, lo siguen los cortocircuitos bifásico y
finalmente el monofásico. En cambio, el tipo mas frecuente es el monofásico (aproximadamente el 75% de los
casos ) y el menos frecuente es el trifásico (aproximadamente el 5% de los casos).
Los objetivos que se buscan al realizar un cálculo de cortocircuito son los siguientes:
•Definir la capacidad de ruptura de los interruptores necesarios en las diversas partes de un sistema de
potencia, para lo que se realiza normalmente un cálculo de cortocircuito trifásico simétrico, debido a que
este tipo de falla produce las corrientes de cortocircuito más elevadas en la mayoría de los casos.
•Ayudar a establecer un sistema adecuado de protección para diversas condiciones de falla, para lo que
se debe realizar un cálculo de distribución de corrientes en la red del sistema eléctrico de potencia tanto
para cortocircuitos simétricos como asimétricos (usualmente el cortocircuito monofásico).

19. En general, el Cálculo de Cortocircuitos debe proporcionar los siguientes resultados:
•La corriente en el punto de falla
•La potencia de cortocircuito en el punto de falla
•La distribución de corrientes de falla en todas las líneas del sistema de potencia
•Las tensiones de falla en todas las barras
Fallas trifásicas
Métodos de cálculo:
•Teorema de Thevenin
•Matriz de impedancias de barra

20. Teorema de Thevenin
•Cortocircuitar las fuentes de tensión para obtener la impedancia de Thevenin.
•Reemplazar el punto de falla por una fuente de voltaje con tensión -Vf
•Calcular I falla como la relación entre la tensión en el nodo antes de ocurrir la falla y la impedancia de
Thevenin
Va
Za
Z1
Vb
Zb
Z2
1
2
3

21. Zi=Za+Z1
Za
Z1
Vf
Zb
Z2
Vf
Zd=Zb+Z2
1
2
3
If If
Zth
If 
Vf
ZiZd
Zi Zd
Zth 
Vf (Zi  Zd)
ZiZd
If 
Podemos calcular las corrientes de
rama teniendo en cuenta el divisor
de corrientes:
Si las impedancias están dadas en
por unidad, se toma Vf como 1.0
en p.u.
IfZd
Zi Zd
Ii 
Zi Zd
Id 
IfZi
2

22. Va
Za
Z1
Vb
Zb
Z2
1
2
3
Se presume que V en el nodo con
falla es igual a 0
Ii Id
Podemos obtener las tensiones en
los otros nodos de la siguiente
forma:
V1 IiZ1 V3  IdZ2
Ejemplo:
Si
Z1  j0.05 pu
Z 2  j0.02 pu
Za  j0.1pu
Zb  j0.12pu
Va Vb 1.00 pu
If 
Vf (Zi  Zd)
j0.15* j0.14
ZiZd
If 
1.0( j0.15  j0.14)
If   j13.80 pu
If 13.8090pu
IfZd
Ii 
j0.15  j0.14
Zi  Zd
 j13.80 * j0.14
Ii 
Ii   j6.66pu
Ii  6.6690pu
IfZi
Id 
j0.15  j0.14
Zi  Zd
 j13.80 * j0.15
Id 
Id   j7.14 pu
Id  7.14 90pu
V1  IiZ1   j13.80* j0.05  0.33pu V3  IdZ2   j7.14* j0.02  0.14 pu

23. Ejercicio:
1
2
3
4
•Calcular la corriente de falla para un corto trifásico en el nodo 2
•Calcular las corrientes a través de cada una de las impedancias debido a la falla trifásica en el nodo 2
•Calcular las tensiones en los nodos 1, 2, 3 debido a la falla trifásica en el nodo 2
Va=1.0pu
j0.1
j0.2
j0.3
j0.2
j0.4
j0.5
Vc=1.0pu
j0.15
Vb=1.0pu
j0.12

24. Matriz de Impedancias
1
2
3
Va
Za
Z12
Z14
Z42
Z23
Z43
Vc
Zc
Vb
4
Zb
Ik YnodoVn



 
34
33
32
31
21
Y44
Y42 Y43

Y41
Y Y Y
Y
Y Y Y
Y1
1 Y12 Y13 Y14

Y 
22 23 24
Ynodo
De acuerdo con la ecuación de nodos:
De donde:
Ykk  Suma de las
admitancias
propias del nodo k
Ykn  Ynk Admitancia mutua
entre los nodos n y
k

25. Matriz de Impedancias
1
2
3
Va
Za
Z12
Z14
Z42
Z23
Z43
Vc
Zc
Vb
4
Zb
1 1 1
1 1 1
1 1 1
43
42
14
44
42
23
12
22
14
12
b
a
Z Z Z Z
Z23 Z43
1 1 1 1
Z Z Z
   )
Y  (
Y33  (  
Z
)
c
  )
Y  (
Y11  (
Z

Z

Z
)
Entonces:
14
13 31
12
21
12
1
1
Z
Y14  Y41 
Z
Y  Y  0
Y  Y 
43
43
34
42
42
24
23
32
23
1
1
1
Z
Z
Z
Y  Y 
Y  Y 
Y  Y 

26. 


 
31 32 33 34

21 22 23 24
1
Z44 
Z42 Z43

Z41
Z Z Z
Z
Z11 Z12 Z13 Z14 
Z Z Z Z 
Z  Ynodo
barra
Definida la matriz de admitancias de nodos obtenemos la matriz de impedancias de barra
De donde:
Zkk  Impedancia de Thevenin vista en el nodok

27. Para una falla en nodo 2:
Aplicando el Teorema de Thevenin se reduce el
circuito:
1
2
3
4
Vf
Za
Z12
Z14
Z42
Z23
Z43
Zc
Zb
If
Ik YnodoVn





 
 
 
 4 
3
1
 0 
 0 
 0 
 V 
V 
 Vf 
nodo
 V 
 I f 
Y
1 3 4
V 
,V 
,V 
Tensiones en los
nodos 1, 3, 4 debido
a la falla
Invirtiendo la matriz de admitancias
obtenemos la matriz de impedancias:






 


 
 0 
 0 
 4 
3
f 
barra
 0 
 I 
f 
 Z
 V 
 V 
V
V1

28. 
 







 


 0 
14

 
11 12 13
 4
3
1
Z44  0 

Z41
Z34 
 0 
Z31
Z24 
I f 
Z22 Z23
Z32 Z33
Z42 Z43
 
Z Z Z Z
V
 V 
 Vf 
 Z
2
1
V 
Reemplazando por la matriz de impedancias:
De donde se obtiene:
V 
 Z I
4 42 f
V 
 Z I
3 32 f
V 
 Z I
1 12 f
Vf  Z22 If
Entonces:
Z
I f

Vf
Como V se asume 1.0 pu yZ
f
están dadas en pu, entonces
pu
Z
f
22 22
1
I 
pu
Zkk
f
1
I 
Antes de ocurrir la falla se supone que no hay corriente de carga, por lo tanto las tensiones en los nodos
son iguales a 1.0 pu
Por superposición:
V post-falla = V pre-falla + V debido a la falla
En general para una falla en nodo k:
22
22
Z
Z
Z
42 f
32 f
1 1 12 f
I  1
Z42
 1 32
Z22
V2  1Vf  0
V 1V 
1 Z
4 4
V 1V 
1 Z I
3 3
V 1V 
1 Z I  1
Z12
Vk  0
y la tensión post-falla en el nodo n:
kk
nk
n
Z
Z
V 1

29. Las corrientes en cualquier parte del circuito se pueden obtener de los voltajes e impedancias, así:
12
Z
I
12 14
14
Z

V1 V2

V1 V4
23
32
Z
I I 
V3 V2
42
42
Z
I 
V4 V2
34
34
Z
I 
V3 V4
a
a
Z
I 
Va V1
b
b
Z
I 
Vb V4
c
c
Z
I 
Vc V3
1
2
3
Va
Za
Z12
Z14
Z42
Z23
Z43
Vc
Zc
Vb
4
Zb

30. Ejercicio 1:
1
2
3
4
Empleando la matriz de impedancias:
•Calcular la corriente de falla para un corto trifásico en el nodo 2
•Calcular las corrientes a través de cada una de las impedancias debido a la falla trifásica en el nodo 2
•Calcular las tensiones en los nodos 1, 2, 3, 4 debido a la falla trifásica en el nodo 2
•Calcular la corriente de falla para un corto trifásico en el nodo 4
•Calcular las corrientes a través de cada una de las impedancias debido a la falla trifásica en el nodo 4
•Calcular las tensiones en los nodos 1, 2, 3, 4 debido a la falla trifásica en el nodo 4
Va=1.0pu
j0.1
j0.2
j0.3
j0.2
j0.4
j0.5
Vc=1.0pu
j0.15
Vb=1.0pu
j0.12

31. 1
2
3
4
Va=1.0pu
j0.1
j0.2
j0.3
j0.2
j0.4
j0.5
Vc=1.0pu
j0.15
Vb=1.0pu
j0.12
Y
1 1 1
0.1 0.3 0.2
1
0.2
0
1
0.2
1 1 1
0.2 0.2 0.4
1
0.4
0
1
1
0.4
1 1
0.4 0.5 0.15
1
0.3
1
0.2
1
0.5
1 1 1 1 1 1 1
0.3 0.2 0.5 0.12 0.5 0.3 0.2
j

32. Z Y 1
0.07j 0.041j 0.014j 0.025j
0.041j 0.121j 0.035j 0.043j
0.014j 0.035j 0.101j 0.023j
0.025j 0.043j 0.023j 0.072j
Z 
Para falla en nodo 2:
2 2
Z 0.121j If
1
Z
2 2
If  8.294j
V1 1
Tensiones de nodo:
Z
1 2
Z
2 2
1 2
Z 0.041j V1 0.662
V3 1
V2 0
Z3 2
Z
2 2
V4 1
Z
4 2
Z
2 2
4 2
Z
3

2
0.035j V3  0.712
Z  0.043j V4  0.641

33. 1
2
3
4
Va=1.0pu
j0.1
j0.2
j0.3
j0.2
j0.4
j0.5
Vc=1.0pu
j0.15
Vb=1.0pu
j0.12
Corrientes a través del circuito:
I
12
V1 V2
j0.2 12
I 3.31j I
14
V1 V4
j0.3 14
I  0.07j I
42
V4 V2
j0.2 42
I 3.205j
I32
V3 V2
j0.4 32
I 1.78j I34
V3 V4
j0.5 34
I 0.142j
Ia
1 V1
j0.1
Ia 3.38j Ib
1 V4
j0.12
Ib 2.992j Ic
1 V3
j0.15
Ic 1.921j
Se puede comprobar que:
12 14
I I I
12 42 32
 8.294j If 8.294j
En nodo 1:
En nodo 3:
Ia I I 0
Ic I34 32
I 0
En nodo 2:
En nodo 4: 14 34 42
Ib I I I 0
Asimismo: Ia Ib Ic 8.294j

34. Análisis de Redes de Secuencia
Ecuaciones generales
Cualquier corriente o voltaje desbalanceado se puede determinar por las componentes de secuencia a partir de las
siguientes ecuaciones:
I A  I1  I2  I0 VA V1V2 V0
I  a2
I  aI  I V  a2
V  aV V
B 1 2 0 B 1 2 0
I  aI  a2
I  I V  aV  a2
V V
C 1 2 0 C 1 2 0
De las anteriores ecuaciones se pueden determinar las cantidades de secuencia a partir de un sistema desbalanceado:
3
3
3
2
1
C
B
A
C
B
A
C
B
0 A
 aI )
 a2
I
I 
1
(I
 a2
I )
 aI
I 
1
(I
I 
1
(I  I  I )
3
3
3
2
1
0
C
B
A
C
B
A
A B C
 aV )
V 
1
(V  a2
V
 aV  a2
V )
V 
1
(V
V 
1
(V V  V )
De estas se deduce que:
3I0  I A  IB IC 3V0 VA  VB VC

35. La aplicación del método de las componentes simétricas al cálculo de cortocircuitos asimétricos significa que cada
componente del sistema de potencia se representa por tres circuitos equivalentes monofásicos, correspondiendo cada
uno a una determinada secuencia.
En cada uno de estos circuitos equivalentes las variables tensiones y corrientes corresponden a una misma secuencia y
las impedancias asociadas a los elementos reciben el nombre de impedancia a la secuencia que corresponde.
Veremos a continuación, los circuitos equivalentes de secuencia de los elementos componentes del sistema.
Líneas:
Las líneas se representan tal como se muestra en los circuitos siguientes.
Impedancia de secuencia
positiva
Impedancia de secuencia
negativa
Impedancia de secuencia
cero
Generalmente: Z1 = Z2  Z0; ya que en secuencia cero es necesario considerar tanto el efecto del retorno por tierra,
como el de los conductores de guarda, en caso que ellos existan, debido a que la corriente se reparte por ambos
caminos

36. E
+
Z1
I1
V1
Generadores:
Los generadores están proyectados para entregar tensiones en secuencia positiva (tensiones trifásicas balanceadas).
Por lo tanto, la red de secuencia positiva está formada por una fuente de voltaje en serie con la impedancia de
secuencia positiva del generador.
Barra de referencia
V1 E  I1Z1
E = tensión del generador
Z2
V2
Z1 = impedancia de secuencia positiva del
generador
La red de secuencia negativa no contiene fuente de voltaje, por lo tanto está formada solamente por la impedancia de
secuencia negativa del generador.
Barra de referencia
V2  I2 Z2
Z2 = impedancia de secuencia negativa del
generador
I2
La barra de referencia para las redes de secuencia positiva y negativa es el neutro del generador.

37. Z0
I0
V0
La red de secuencia cero depende de la forma en que se aterrice el neutro del generador.
•Si el neutro del generador está solidamente aterrizado:
Barra de referencia
V0  I0 Z0
Z0 = impedancia de secuencia cero del
generador
Z0g+3Zn
I0
V0
•Si el neutro del generador está aterrizado a través de una impedancia Zn:
El voltaje de la red de secuencia cero es igual a la suma del voltaje de secuencia cero a través del generador más el
voltaje de secuencia cero a través de la impedancia Zn.
A través de la impedancia Zn circula In, donde In = IA+ IB+ IC = 3I0. Por lo tanto el voltaje de secuencia cero a través de
Zn es -3I0Zn.
El voltaje de secuencia cero a través del generador es -I0Z0g.
Entonces el voltaje de secuencia cero para el sistema es -I0(Z0g+3Zn)
Barra de referencia
V0  I0 (Z0 g  3Zn)
Z0g = impedancia de secuencia cero del
generador

38. Z0g I0
•Si el neutro del generador no está aterrizado:
En este caso se supondría que el generador está aterrizado a través de una impedancia Zn con valor infinito, por lo
que la red de secuencia cero se comportaría como un circuito abierto. En este caso no hay circulación de corriente de
secuencia cero.
Barra de referencia
I0  0
V0
Transformadores:
Para los transformadores la impedancia de secuencia positiva es igual a la de secuencia negativa, ya que éste se
comporta de igual manera independientemente de la secuencia de las fuentes voltajes.
Impedancia de secuencia
positiva
Impedancia de secuencia
negativa
Generalmente, en el caso de los transformadores Z1 = Z2  Z0. Pero hay que tener en cuenta el grupo de conexión y
de la existencia o no de neutros conectados a tierra para saber si hay corrientes de secuencia cero.

39. Redes de secuencia cero para transformadores de dos devanados

40. Redes de secuencia cero para transformadores de tres devanados
1
2
2
pt
st
s ps
st
pt
p ps
Zt 
2
(Zpt  Zst  Z ps )
Z 
1
(Z  Z  Z )
Z 
1
(Z  Z  Z )
t
s
Z pt  Z p  Z
Zst  Zs Zt
Z ps  Z p Z

41. Análisis de algunos tipos de fallas
1) Falla monofásica a través de una impedancia Zf
De la figura anterior se observa que:
Ib  Ic  0 Va  ZF Ia
a
B C
A
a
C
B
A
a
B C
3
3
3
1
3
3 3
2
2
1
0 A
I 
1
(I  a2
I  aI ) 
1
I
 aI  a I )  I
I 
1
(I
I 
1
(I  I  I ) 
1
I
Las componentes simétricas de corriente quedan:
Por lo tanto:
2
1
I0  I1  I2 
3
Ia
Ia  3I0  3I1  3I (1)

42. Para las componentes simétricas de voltaje se tiene:
3
3
1
C
B
2 A
C
B
1 A
V 
1
(V  a2
V  aV )
V 
1
(V  aV  a2
V )
V0 
3
(VA VB VC ) Por lo tanto:
V0 V1V2 Va  ZF Ia
De (1):
V0 V1 V2  3I0 ZF  3I1ZF  3I2 ZF (2)
De las ecuaciones (1) y (2) se deduce que las redes de secuencia positiva, negativa y cero quedan conectadas en
serie, como se muestra a continuación:
E
+
I1
V1
3ZF
Z1
V2
I2
Z0
Z2
V0
I0
F
F
E
3E
1
1
 Z2  Z0  3Z
Ifalla  Ia  3I0 
Z
 Z2  Z0  3Z
I0  I1  I2 
Z
Del circuito se tiene:
0
0
I  aI  a2
I  I
c 1 2
I  a2
I  aI  I  0
b 1 2
 0

43. Del circuito también se tiene:
V2  I2 Z2 
E
F
Z0
Z1  Z2  Z0  3Z
V0  I0 Z0 
E
F
F
1
EZ1
Z1  Z2  Z0 3Z
Z2  Z0 3ZF

Z  Z  Z 3Z
V1 E  I1Z1  E 
E
F
2 0
Z2
Z1  Z2  Z0  3Z

Por lo tanto los voltajes de fase se pueden calcular a partir de sus componentes simétricas así:
Va V1V2 V0
V  a2
V  aV V
b 1 2 0
V  aV  a2
V V
c 1 2 0
Si la falla es directa a tierra, entonces ZF = 0 y:
0
3E
Z1  Z2 Z
Ifalla  Ia  3I0  Ib  Ic  0 Va  0
E
1
Z1  Z2  Z0
Z2 Z0
V 
0
Z2
2
Z1  Z2 Z
V   E
0
Z0
0
Z1  Z2 Z
E V  

44. 2) Falla bifásica:
De la figura anterior se observa que:
Vb Vc
b
c
b c
Ib
Ib
3
1
3
3
1
3
a2
2
2
0 a
 a
I2 
3
(Ia  a I  aIc )
a a2
I1  (Ia  aIb  a I ) 
I 
1
(I  I  I ) 0
Ia  0
Ib  Ic
Las componentes simétricas de corriente quedan:
Por lo tanto:
2
1
I  I
I0  0 (1)

45. Para las componentes simétricas de voltaje se tiene:
3
)
1
3
2
b c
2 a
c
b c
0 a
V 
1
(V  a2
V  aV )
V1
3
(Va  aVb  a V
V 
1
(V  V V ) Como: Vb Vc
Entonces: V1V2 (2)
E
+
Z1
I1
V1
I2
V2
Z0
I0
V0
Z2
2
1
E
Z  Z
I1  I2 
De las ecuaciones (1) y (2) se deduce que las redes de secuencia positiva y negativa quedan conectadas en paralelo,
y la red de secuencia cero queda desconectada:
Del circuito se tiene:
2
1
1
0
1
0
2 0
E
E
 Z
 Ib   j 3
Z
 I (a  a2
)
I  aI  a2
I  I
c 1 2
Z1 Z2
 j 3
 I (a2
 a)
I  a2
I  aI  I
b 1 2
Ia  I1  I  I  0

46. Del circuito también se tiene:
V2  I2 Z2 
V0 0
E
2
1
Z2
2
1
EZ1
Z  Z

Z  Z
V1 E  I1Z1  E
E
2
1
Z2
Z  Z
Por lo tanto los voltajes de fase se pueden calcular a partir de sus componentes simétricas así:
Va V1V2 V0  2V1
V  a2
V  aV V  V
b 1 2 0 1
V  aV  a2
V V  V
c 1 2 0 1
Se observa que:
V1 V2
Vb Vc

47. Para fallas trifásicas vimos que la corriente de falla se calcula de la siguiente manera:
Zth
If 
Vf
Por ser una falla balanceada, la impedancia Zth corresponde a la impedancia de secuencia positiva y al
considerar Vf como 1.0 en pu, podemos escribir la ecuación anterior de la siguiente forma:
1
Z
I 
1
3
Para fallas bifásicas la corriente de falla es igual a:
E
b
Z1 Z2
I  j 3
Considerando que Z1 = Z2 y asumiendo que E = 1.0 en pu, la magnitud de las corrientes de fallas bifásicas se
puede calcular así:
1 1 1
E 3 1 3
 
 Z 2 Z 2
I3
I2  3
Z
3
I2 
2
I3
Por lo tanto:
Para fallas monofásicas la corriente de falla es igual a:
0
1 2 0 1
3E 3

Z  Z  Z 2Z Z
I 
1
Por lo que: I1  I3 si Z0 = Z1, y I1  I3 si Z0 < Z1

48. Componentes de un sistema de protecciones
La protección de un equipo eléctrico puede ser tan simple como un fusible o tan compleja como los modernos
relés de tipo numérico, que hacen uso incluso de enlaces de fibra óptica para transmitir la información de un
punto a otro. Por esta razón, una definición de Sistema de Protecciones debe ser lo suficientemente amplia
como para incluirlas a todas.
Sistema de Protecciones es el conjunto de elementos y de sus circuitos de control asociados que se encuentran
interconectados o dependientes entre sí, cuya función es proteger a un equipo o a un conjunto de equipos. Este
conjunto de elementos operará bajo condiciones predeterminadas, usualmente anormales, desconectando un
elemento del sistema de potencia o emitiendo una señal o ambas cosas. Bajo la perspectiva de esta definición y
tratando de referirse siempre a los casos más generales, los componentes de un sistema de protecciones, tal
como se muestra en la figura siguiente, son :

49. Transformadores de medida
Los transformadores de medida son los elementos que permiten obtener la información acerca de las condiciones
de operación de un sistema de potencia, en la forma de señales secundarias de corriente o de tensión
proporcionales a las magnitudes primarias. Bajo este término común se agrupan los transformadores de corriente
TC y de potencial TP, para diferenciarlos de los transformadores comunes.
Relés de protección
Son los elementos que reciben la información de los transformadores de medida y que son capaces de discriminar
entre una condición normal y anormal. Cuando el relé detecta una condición anormal inicia su acción (“opera”),
generalmente a través de contactos que se cierran o se abren y que, en forma directa o indirecta, habilitan los
circuitos de apertura o desenganche de los interruptores de potencia.
Interruptores de potencia
Dispositivos que cumplen con la función de aislar o desconectar los equipos, ya sea por operación de las
protecciones o de las personas que manejan el sistema eléctrico. Se denominan interruptores de potencia para
diferenciarlos de otros dispositivos que no son capaces de interrumpir un circuito en condiciones de falla por no
tener la capacidad de ruptura necesaria, aún cuando están diseñados para aislar partes del circuito.
Circuitos de control
Conjunto de elementos que interconectan a los tres componentes anteriores. Entre estos elementos se puede
mencionar: alambrados; regletas de conexiones; switches; relés auxiliares; lámparas de señalización; dispositivos
anunciadores; etc. Se analizarán a continuación, las principales características de los distintos elementos que
componen los sistemas de protecciones.

50. Transformadores de medida (TM)
Los transformadores de medida cumplen con varios objetivos como son:
Aislarse del circuito de Alta Tensión: Puesto que no existen ni serían prácticos instrumentos o relés para
conexión directa a la alta tensión, se usan transformadores que cumplen con la función de entregar corrientes o
voltajes en baja tensión con el objeto de proteger tanto a los instrumentos como a las personas que los operan.
Disponer de magnitudes normalizadas: Los secundarios de los TM entregan valores normalizados de modo de
facilitar la utilización de instrumentos u otros dispositivos que por tener un bajo nivel de aislamiento resultan
pequeños y económicos.
Efectuar medidas a distancia: Al disminuir los niveles de las magnitudes a medir y al estar aislados de la alta
tensión, se hace posible instalar los elementos de medida y protección a distancias mas o menos alejadas del
punto de ubicación de los TM. Sin embargo, esta distancia no puede ser mayor de unos 100 a 150 m, puesto
que los conductores comienzan a ser una carga apreciable que compromete la exactitud de las medidas. Con la
aparición de los relés de estado sólido y de los transductores electrónicos de medida, las distancias
mencionadas han podido superarse largamente.
Realizar aplicaciones en protecciones y medidas: Interconectando adecuadamente los secundarios de los TM,
se pueden obtener otras magnitudes de gran utilidad en la aplicación de algunas protecciones y medidas. A
modo de ejemplo, se pueden mencionar los dos circuitos que se muestran en las figuras siguientes, que
permiten obtener voltajes y corrientes de secuencia cero, respectivamente.

51. Proteger instrumentos: Esta aplicación es particularmente válida en el caso de los TC destinados a medidas, ya
que al ocurrir un cortocircuito se aprovecha un bajo índice de saturación del núcleo para provocar un elevado
error negativo en la corriente secundaria, de modo que ésta no se eleve muy por encima de los valores
nominales. Se protegen de esta manera las bobinas de corriente de instrumentos tales como: amperímetros;
vatímetros; fasímetros; etc.
Obtención de voltaje de secuencia cero Obtención de corriente de secuencia cero

52. Transformadores de potencial (TP)
Son los transformadores de medida utilizados para reducir las tensiones primarias del sistema de potencia a
tensiones secundarias de rangos normalizados (110-120 volt), en forma directamente proporcional.
El transformador de potencial es muy similar a un transformador de potencia ya que ambos tienen la finalidad de
cambiar el nivel de la tensión. Un transformador de potencia está destinado a servir una carga sin exceder un
aumento de temperatura especificado. El transformador de potencial se define, en cambio, en términos de la
máxima carga (o burden) que es capaz de entregar sin exceder los límites de error de relación y de ángulo
especificados; esto significa que la carga que es capaz de servir, sin exceder los valores permitidos de aumento de
temperatura, puede llegar a ser hasta diez veces superior a su burden nominal.
Circuito equivalente
y diagrama fasorial
de un TP referidos
al lado primario

53. Ejemplo: Sea,
RTP = 110000/110
Vp = 110000
Vs = 109.89
Entonces el error de relación sería
El error de fase es la diferencia angular entra los voltajes primario y secundario ()
Es positivo cuando el voltaje secundario se adelanta al voltaje primario
Errores:
Los errores de relación y fases del transformador se pueden calcular utilizando el diagrama vectorial anterior.
El error de relación se define como: RTP Vs Vp
x100%
Vp
donde:
RTP es la relación de transformador de potencial
Vp es la tensión primaria
Vs es la tensión secundaria
Si el error es positivo, entonces el voltaje secundario excede a la tensión nominal.
110000
109.89 110000
110 x100%  0.1%
110000

54. Todos los transformadores de potencial deben cumplir con las tablas siguientes:
Clase de
precisión
0.25 - 1.0 x tensión nominal
0.25 - 1.0 x burden nominal a 0.8fp
Error de relación
(%)
Error de fase
(min)
0.1 +/- 0.1 +/- 5
0.2 +/- 0.2 +/- 10
0.5 +/- 0.5 +/- 20
1.0 +/- 1.0 +/- 40
3.0 +/- 3.0 no se especifica
Errores límites para TPs de medida
Clase de
precisión
0.25 - 1.0 x burden nominal a 0.8fp
0.05 - Vf x tensión nominal
Error de relación
(%)
Error de fase
(min)
3P +/- 3.0 +/- 120
6P +/- 6.0 +/- 240
Errores límites para TPs de protección
De la última tabla, Vf es un límite superior de la tensión de operación, expresada en por unidad de la tensión
nominal. Es importante para una correcta operación de las protecciones y operación bajo condiciones de fallas
desbalanceadas en sistemas no aterrizados o aterrizados a través de impedancias, lo que resulta en un incremento
en la tensión de las fases no falladas.
Factor de
voltaje Vf Tiempo
Condiciones de aterrizamiento
Devanados primariosTP Sistema
1.1 Ilimitado No aterrizado Aterrizado o no
1.5 30 s Aterrizado Aterrizado
1.9 30 seg u 8 horas Aterrizado No aterrizado

55. Protección de los TPs
Los TPs pueden ser protegidos por fusibles en el lado primario y para tensiones de hasta 66 kV. Para tensiones
mayores, los fusibles generalmente no tienen suficiente capacidad de interrupción.
El secundario de un TP siempre debe estar protegido por fusibles o mini circuit breakers MCB, el cual debe estar
ubicado lo más cerca posible del TP.
Un cortocircuito en el secundario producirá corrientes de muchas veces la salida nominal, causando un
sobrecalentamiento. Aunque se instalen fusibles en el primario, éstos no despejarán fallas en el lado secundario
debido al valor muy bajo de corriente.
Obtención del voltaje residual
Durante una falla a tierra, la suma de las tensiones de fase no es igual a cero, por lo que el voltaje residual se puede
medir conectando los devanados secundarios de los TPs en “delta abierta”.
A menudo, los TPs están provistos con un secundario conectado en estrella normal y un devanado “terciario”
conectado en delta abierta.
Si los TPs no están provistos del devanado “terciario” para la delta abierta, se pueden utilizar TPs auxiliares con
conexión estrella / delta abierta, energizados desde el lado secundario de los TPs principales, tal como se muestra a
continuación.

56. Los TPs auxiliares deben cumplir los requerimientos para soportar el factor de voltaje Vf

57. Transformadores de corriente (TC)
Son los transformadores de medida destinados a entregar una corriente secundaria proporcional a la que circula por
su enrollado primario. Este enrollado está conectado en serie con el circuito de poder que se pretende medir. En
cualquier caso, su impedancia es despreciable comparada con la del circuito de potencia, aún si se considera el
efecto de la impedancia del circuito secundario transferido.
Se construyen como elementos monofásicos, cuyo primario tiene muy pocas espiras (normalmente una sola). El
núcleo puede ser de material ferromagnético o de aire. En el primer caso poseen una potencia de salida importante,
por lo que son aptos para usar con relés electromecánicos; sin embargo, no existe una proporcionalidad total entre
las corrientes de los enrollados primario y secundario, debido a las características no lineales de los materiales
utilizados en el núcleo. Los TCs con núcleo de aire tienen baja potencia de salida por lo que sólo se pueden usar
con relés del tipo estático, sin embargo, la corriente secundaria es siempre proporcional a la corriente.
Según las características constructivas de la bobina primaria, los TT/CC se clasifican en:
•Tipo bobinado: La bobina primaria se enrolla con una o más vueltas al núcleo de hierro. Las bobinas
primarias y secundarias se encuentran aisladas entre sí y también están aisladas del núcleo

58. •Tipo barra: Consiste en un conductor fijo, aislado, en forma de barra o tubo, como bobina primaria que
atraviesa el núcleo de hierro, en general de forma toroidal al que se ha enrollado la bobina secundaria.
•Tipo ventana: Es aquel que consta solamente de una bobina secundaria enrollada alrededor de un núcleo de
hierro y en el cual la bobina primaria no forma parte del TC propiamente tal.
•Tipo bushing: Tiene un núcleo de hierro toroidal al cual se ha enrollado la bobina secundaria pero no tiene
bobina primaria. Va montado en el bushing de los transformadores de potencia y la bobina primaria la forma
el cable conductor del circuito de potencia.

59. Circuito equivalente y diagrama fasorial
A continuación se muestra el circuito equivalente y el diagrama fasorial para un TC. Las impedancias están referidas
al lado primario. Ze es la impedancia de fuga o equivalente del TC, normalmente de valor pequeño. Z0 es la
impedancia de excitación y Zb es la impedancia de carga o burden
I1  I0 aI2
En un transformador de corriente interesa que el error de relación “a” y de ángulo “β” sean mínimos, por lo que, de
las expresiones y figuras anteriores, se observa que es necesario disminuir la corriente de excitación I0. Por esta
razón, si se considera que tanto Ze como Zb son parámetros constituidos por elementos no saturables, el análisis
del comportamiento de un TC se efectúa a través de su característica de excitación.
1 2
N I
de donde a 
N2

I1
es la relación de transformador de corriente o RTC

60. La magnitud de la corriente de excitación I0 de un transformador, depende del tipo de material del núcleo y del flujo que
deba tener para satisfacer el burden requerido. En los transformadores de corriente, la carga representa una caída de
voltaje por impedancia, que en la figura corresponde a aI2 Zb/a2, la que, si se desprecia la caída en Ze, es igual a I0 Z0, lo
que determina el valor de I0 y por lo tanto del flujo, además de determinar el valor de Z0 como función de la característica
de excitación.
Para que la relación real de corrientes sea lo más ajustada posible a la RTC, I0 debe tender a cero, o bien: Z0>>(Ze+Zb/a2).
Como resultado de estas consideraciones se puede concluir que:
 El núcleo debe ser de muy buena calidad para trabajar a niveles bajos de saturación y con pocas pérdidas.
No se debe trabajar con cargas superiores a la nominal ya que si la impedancia de la carga es muy alta, aumenta
la corriente de excitación y consecuentemente el error de relación y de ángulo.
No se debe trabajar con el secundario en circuito abierto porque en este caso, el voltaje desarrollado será limitado
solamente por la impedancia de magnetización. En estas condiciones: I1=I0, lo que trae como consecuencia la
saturación, altas pérdidas y sobretemperatura en el núcleo, junto con elevados voltajes máximos en bornes
secundarios.

61. Característica de excitación
Las figuras siguientes muestran la característica de excitación de un TC y el circuito empleado para obtenerla. Para fines
de estudio se ha exagerado el codo de saturación. En la práctica esta curva es mas redondeada y por eso se acostumbra
dibujarla en papel log-log. De esta forma se puede definir con mayor precisión el “punto de saturación”, es decir, el punto
donde la relación dV0/dI0 deja de ser constante. Esta curva se puede dividir (en forma aproximada), en cuatro zonas:
− El pie de la curva de 0 de 20 Volts, aproximadamente.
− Zona de linealidad, entre 20 y 160 Volts
− Zona del codo de saturación de 160 a 180 Volts
− Zona de saturación, a partir de los 180 Volts.
Para esta curva la zona de linealidad determina una impedancia de aproximadamente 53,33 ohm. A partir de los 180
Volts, la impedancia de excitación empieza a decrecer desde un valor de 36 ohm, debido a la saturación, es decir, en el
codo de saturación Z0 disminuye de 53,33 a 36 ohm aproximadamente.

62. Punto de saturación
Para establecer las características de operación de los TC con corrientes superiores a la nominal, resulta necesario
definir su punto de saturación. En este contexto, hay varios criterios y normas, algunas de las cuales se describen a
continuación:
Criterio de la EEC
La English Electric Corporation (EEC) ha definido al “punto de saturación” de la curva de excitación, como el punto en el
cual un incremento de un 10% de la tensión secundaria, produce un 50% de aumento en la corriente de excitación. Este
punto puede ser considerado como un límite práctico, sobre el cual no se mantiene la razón de transformación
especificada. Según esta definición, si la impedancia de excitación en el límite de la zona lineal, es Z0=V0/I0, se tiene que
la impedancia de excitación en el punto de saturación, Z0s=V0s/I0s corresponde al 73,33% de Z0.
De acuerdo con el gráfico de la figura anterior, Z0=53,33 ohm y por lo tanto, Z0s=39,11 ohm, en que tanto Z0 como Z0s
corresponden a valores medidos en el secundario
Efectos de la variación del burden sobre la corriente secundaria
La carga externa conectada al secundario de un transformador de corriente recibe el nombre de Burden. Este se
expresa, generalmente, en términos de impedancia y factor de potencia. En algunos casos se expresa también como los
Volts-Amperes (VA) disipados en la impedancia, a corriente nominal secundaria, con el factor de potencia
correspondiente. Las variaciones que puede experimentar el burden conectado al secundario de un T/C, producen
importantes efectos sobre su comportamiento. Considerando los resultados determinados según el criterio de la EEC, se
puede visualizar el efecto que el burden tiene sobre la corriente secundaria.

63. De acuerdo con la característica de excitación del TC de la figura anterior, la razón entre las corrientes se mantiene hasta
un voltaje secundario de 160 Volts. ¿Hasta qué valores de sobrecorriente se mantiene dicha razón, en función de la
carga?. Para este efecto supóngase que, como Ze<< Zb, se puede despreciar Ze y por lo tanto, en la característica de
saturación, ZbI2=160 Volts, expresados en términos secundarios. Los resultados se muestran en la tabla siguiente. El
valor “n” corresponde a la razón entre la corriente secundaria que puede circular, considerando que se mantiene la
relación de transformación del TC y la nominal secundaria (5 Amperes, en este caso) y puede ser considerado como un
“índice de sobrecorriente”. En la tabla se aprecia que a medida que aumenta la carga, la corriente secundaria que puede
circular, manteniendo la razón de transformación, disminuye, de la misma forma que lo hace el factor “n”.
Zb (Ohm) I2 (Amp) n = (I2)/5
1 160 32
2 80 16
4 40 8
8 20 4
Efectos de la variación del burden sobre la razón de transformación
Para analizar el efecto que la carga ejerce sobre la razón de transformación, se considerará despreciable el error angular,
definiendo el error de relación Er, a partir de la relación nominal RTCN y la relación real RTCR
1
0
I
I
r
E  x100%
Por lo tanto, el valor absoluto del error de razón, expresado en función de la corriente primaria I1 es:
N
N
r
RTC
RTC  RTCR
E 

64. Por otra parte, considerando el circuito equivalente del TC y despreciando Ze, se puede determinar I0 e I1, por lo que la
expresión anterior se puede escribir en función de la impedancia de carga Zb de la siguiente forma:
x100%
Zb
r Z a2
Z
b 0
E 
En la expresión anterior: a2Z0 representa la impedancia de excitación referida al secundario, la cual, en este caso es de
53,33 ohm. Si, por ejemplo, Zb = 1,0 ohm, entonces el error de razón será del 1,84%. Si el burden aumenta al doble, el
error sube a 3,61%, o sea, prácticamente al doble.

65. Punto “knee” según ANSI
El American National Standard Institute (ANSI, C57.13-1978), define lo que denomina el punto “knee” (rodilla) o punto
efectivo de saturación como el punto en que la curva de excitación es tangente a la línea trazada a 45º de la horizontal.
En la figura siguiente, la recta trazada en línea de segmentos, desde el punto “A” es el lugar geométrico de la intersección
de esta tangente con cada una de las curvas correspondientes a las distintas razones del TC. Por esta razón , al punto “A”
se le denomina “ANSI knee”
Punto “knee” según IEC
La International Electrotechnical Commission (IEC), define el punto “knee” (rodilla) o punto efectivo de saturación como la
intersección de las rectas trazadas extendiendo las partes saturada y no saturada de la curva de excitación.
En la figura anterior, corresponde al punto “B”, que por esta razón, se denomina “IEC knee”, el que como se aprecia,
determina un valor de voltaje más elevado que el “ANSI knee”; es decir, según la IEC, el límite de la zona considerada
lineal es superior al determinado por ANSI.

66. Precisión del T/C utilizado en protecciones
El comportamiento de un relé de protección depende de la clase de precisión que el TC mantenga no sólo a corriente
nominal sino que también para las corrientes de falla. El grado de precisión para altas corrientes depende de la sección
transversal del núcleo y del número de vueltas del secundario. Mientras mayor sea la sección transversal del TC, mayor es
el flujo magnético que puede desarrollarse antes de alcanzar el punto de saturación.
La saturación del TC genera un alto error en la relación de transformación. Por otro lado, un gran número de vueltas en el
devanado secundario requiere de un menor flujo magnético para inducir la corriente secundaria que debe circular a través
del relé.
Al respecto, existen diversas formas de determinar el comportamiento de un TC, tanto en forma analítica como por
aplicación de las normas. A continuación se considerarán algunas de ellas.
Cálculo directo
Se hace uso de la fórmula clásica del transformador, es decir, la ecuación que corresponde a la expresión general de
tensión inducida en la bobina de un transformador de N espiras, con núcleo de sección A, a una densidad de flujo máxima
Bmax y frecuencia f.
V sec  4,44 fNABmax
despreciando la resistencia óhmica y la ecuación que relaciona la tensión secundaria correspondiente a la suma de las
caídas debidas a la circulación de corriente I2 por las impedancias de carga Zb, de fuga Ze y de los conductores ZL:
V sec  I2 (Zb  Ze  ZL )
De donde se puede obtener
Bmax 
I2 (Zb  Ze  ZL )
4,44 fNA

67. Si el Bmax resultante es mayor que el valor correspondiente al del material del núcleo, el TC no podrá usarse sin que los
errores de medida sean mayores que los nominales
Por aplicación de las normas ASA (ASA C57.13-1954)
Estas normas especifican generalmente, el voltaje máximo que puede obtenerse en bornes secundarios, sin exceder el
error especificado. En el caso de las normas ASA (American Standard Association), se consideran los siguientes
aspectos:
− Tipo de TC: H , de alta impedancia interna y L, de baja impedancia interna
− Precisión de sobrecorriente: 2,5 y 10% de error nominal de razón
− Tensiones secundarias: 50-100-200-400-800 Volts.
−Corrientes nominales secundarias: 0,1-1,0-5,0 Amperios. Los valores mas bajos se usan cuando la carga
secundaria se encuentra alejada de los TCs. El valor de uso normal es de 5,0 Amperios.
− Factor de potencia de la carga: 0,5 o 0,9 (Ambos inductivos)
La norma ASA designa a los TC por medio de dos cifras y una letra colocada entre ellas. (Además de los valores usuales
como: relación de transformación, corriente nominal secundaria, etc.)
La primera cifra indica el error máximo de relación que puede producirse siempre que no se exceda el voltaje en bornes
secundarios que especifica la segunda cifra. La letra colocada al centro puede ser H ó L.
En los transformadores tipo H, las dos cifras mencionadas son válidas para corrientes secundarias de 5 a 20 veces la
nominal (Ejemplo: T/C tipo 2,5H400). En los transformadores tipo “L”, las cifras tienen validez para 20 veces la corriente
nominal, solamente (Ejemplo: T/C tipo 2,5L400).

68. Por aplicación de las normas ANSI/IEEE (ANSI/IEEE Standard C57.13-1978)
Las norma ANSI/IEEE C57.13-1978 definen las clases de precisión de los T/C con las letras T y C junto a un número de
clasificación. La letra T (clase H, antes de 1968) indica que este error ha sido determinado experimentalmente mientras
que la letra C (Clase L, antes de 1968) indica que el error inducido en la razón de transformación puede calcularse.
Clases de precisión según IEC
Las normas IEC distinguen entre TC para uso en medida y en protecciones. Los TC a usarse en sistemas de
protecciones se designan con la letra P y se especifican las siguientes características:
− Potencias nominales: 2,5-5,0-15 y 30 VA
− Clases de precisión: 5 y 10%
− Factores límites de precisión (FLP): 5-10-15-20 y 30.
− Corrientes nominales secundarias: 1,0-2,0 y 5,0 Amperes. El valor preferido es de 5,0 Amperes.
Por ejemplo, un TC designado como 15 VA Clase 10 P 20; significa que su capacidad permanente es de 15 VA, con un
error no mayor del 10%, siempre que su voltaje secundario no sea mayor de 20 veces el nominal.
nom
V sec 
VA

VA
In In In2
max permisible
V sec 
VA
FLP Burden
O más exactamente:
Adicionalmente se puede determinar en forma aproximada el voltaje de saturación del TC así:
Vsat  Vsecmax
Vsat 
VA
FLP
In
VA
Vsat  (  R In)FLP
In TC
Donde R es la resistencia interna del TCsuministrada
TC
por el fabricante

69. Para el TC de 15 VA Clase 10 P 20, podemos hacer los siguientes cálculos:
nom
5
max
5
V sec 
15
20 60Volt

15
 0.6
52
permisible
V sec 
15
 3Volt Burden
Vsat  60Volt
Para determinar si un TC es apto para la aplicación de protecciones que se esté haciendo, se debe hacer lo siguiente:
- Conocer las resistencias tanto de los relés, como de los conductores y del TC.
- Conocer la corrientes máxima (falla) que pueda circular por el TC.
- Calcular el voltaje secundario de operación para el nivel de corriente de falla, el cual debe ser menor que el
voltaje de saturación del TC.
Por ejemplo, sea un TC de relación 1000/5 y 7.5 VA 10P20, y la corrientes de falla es 8500 A, y :
Suministrado por el fabricante del TC
Resistencia de los conductores desde el TC hasta los relés
Suministrado por el fabricante del relé
1000/5
8500
V sec  I2 (RTC  RL  RR )
RTC  0.26
RL  0.02
RR  0.15
Por lo tanto
In
Vsat  (
VA
 R In)FLP  (
7.5
 0.26*5)20  56
TC Vsat  56Volt
Por lo que se cumple que:
5
V sec Vsat
V sec Vsat
(0.26  0.02  0.15) 18.28Volt V sec 18.28Volt

70. De los resultados anteriores:
Vsat  56Volt
1000/5
8500
(0.26  0.02  0.15) 18.28Volt
V sec  I2 (RTC  RL  RR )
5
2
2
2
(0.26  0.02  0.15)

I max / In 
130
 26
130A
I max
Vsat
(R  R  R )
Vmax
I max
(RTC  RL  RR)
L R
56
TC
Vmax  I2 max(RTC  RL  RR )
Este TC se satura a partir de 26 veces la corriente nominal secundaria y con el burden asumido de 0.02 y 0.15
ohmios

71. Especificaciones técnicas de un TC
Las principales características técnicas que deben ser indicadas al momento de seleccionar un TC son las siguientes:
Corriente nominal
La corriente nominal máxima debiera ser igual o mayor a la máxima corriente de operación del circuito en donde se
conectará el T/C. La magnitud de la corrientes de inrush también debe ser considerada, específicamente con respecto al
efecto que puede tener en instrumentos de medidas o en relés de protecciones.
Factor de sobrecarga
Es una constante dada por el fabricante, que indica cual es la máxima corriente primaria que puede circular a través del
TC en forma permanente sin exceder la temperatura máxima de los enrollados para una temperatura ambiente de 30º C.
El factor de sobrecarga (Rating Factor RF) normalizado es de 1,0-1,33-1,5-2,0-3,0 o 4,0. Por ejemplo un TC de 100/5 con
un RF igual a 1,5 puede operar en forma permanente con 150 A.
Corriente térmica de tiempo corto. Límite de solicitaciones térmicas
Es el valor efectivo de la máxima corriente que, circulando durante un segundo por el primario de un TC con uno de sus
secundario en cortocircuito, provoca elevaciones de temperatura que no exceden de 250 ó 350ºC, según la clase de
aislación sea A ó B. Este límite, designado como Ith es entregado por el fabricante y se da como un número de veces la
corriente nominal del TC durante un segundo. Para la correcta aplicación de un TC, y considerando tiempos de duración
de la falla de hasta 5 segundos, es conveniente que se cumpla la condición dada por la ecuación siguiente, donde Icc es
el valor efectivo de la máxima corriente de cortocircuito en el punto de instalación del TC y f es la frecuencia del sistema:
Ith  Icc t  0.05*50 / f

72. Para el ejemplo anterior:
Ith  Icc t  0.05*50 / f  8500 1 0.05*50 / 60  8.6kA
Ith debe ser mayor o igual que 8.6 kA
Límite de solicitaciones dinámicas. Corriente mecánica de tiempo corto
Es la máxima corriente asimétrica de cortocircuito que el TC es capaz de soportar sin que se dañe físicamente. Este tipo
de corriente se especifica solamente en TC tipo bobinado. Corresponde al valor máximo de la amplitud de la corriente del
primer ciclo que circula por la bobina primaria estando el secundario en cortocircuito. Se le denomina también corriente
dinámica y se define según la ecuación
Idin 1.8 2Ith  2.542Ith
Voltaje nominal
Corresponde a la tensión entre líneas del circuito de potencia donde se va a instalar el transformador de corriente. Los TC
pueden operar hasta con un 10% por sobre el voltaje nominal.
Polaridad y conexiones
Las polaridades relativas del primario y secundario de un TC se identifican colocando marcas y/o símbolos H1, H2 para los
terminales primarios y X1, X2 para los terminales del secundario. Según esta convención, si H1 y X1 son bornes de igual
polaridad, cuando la corriente primaria “entra” por H1, la corriente secundaria “sale” por X1. Igualmente se puede utilizar
P1, P2 para los terminales primarios y S1, S2 para los terminales del secundario.

73. P1
P2
S1
S2
Conexión delta: Cuando se quiere eliminar las corrientes de secuencia cero.
Conexión estrella: Particularmente apropiada cuando se requiere obtener corrientes de secuencia cero.

74. Aplicaciones
Los TC se usan tanto en medidas como en protecciones. Cuando se usan para medidas, requieren de una alta precisión y
de una característica idealizada como la que se muestra en la figura siguiente, con el fin de que protejan adecuadamente a
los instrumentos conectados a sus secundarios cuando existan altas corrientes en el sistema de potencia en que se
encuentran, como es el caso de una falla, por ejemplo.
Para uso en protecciones, en cambio, es conveniente que no exista saturación con elevadas corrientes primarias, es decir,
que se mantenga una precisión aceptable cuando ocurran fallas en el sistema. Para este caso es conveniente una
característica como la de la figura siguiente.

75. Error compuesto
Este error es definido por la norma IEC 60044-1 y debe cumplir con los valores dados en la siguiente tabla:
Clase de
precisión
+/- (%) error
% corriente 50 120
3 3 3
5 5 5
Clase de
precisión
+/- (%) error
% corriente 5 20 100 120
0.1 0,4 0,2 0,1 0,1
0.2 0,75 0,35 0,2 0,2
0.5 1,5 0,75 0,5 0,5
1.0 3 1,5 1 1

76. Tecnologías de relés
Relés electromecánicos
Estos fueron las formas iniciales de relés de protección que se utilizaron en los sistemas de potencia.
Funcionan con el principio de la fuerza mecánica que causa la operación de un contacto en respuesta a un
estímulo. La fuerza mecánica se genera a través del flujo de corriente en uno o más devanados de una o varias
bobinas, de ahí el nombre electromecánico.
Relé electromecánico de tiempo instantáneo Relé electromecánico temporizado

77. Relé electromecánico de sobrecorriente temporizado e instantáneo

78. Relé electromecánico de sobrecorriente temporizado e instantáneo

79. Relés estáticos
Su diseño está basado en el uso de elementos electrónicos análogos en vez de bobinas e imanes para crear la
característica del relé. Las primeras versiones utilizaron elementos discretos como transistores y diodos en conjunto
con resistencias, condensadores, inductores, etc., pero los avances de la electrónica permitieron el uso de circuitos
integrados lineales y digitales en las versiones posteriores para el procesamiento de las señales e implementación de
funciones lógicas.
El término estático se refiere a que el relé no tiene partes móviles. No es estrictamente el caso para un relé estático ya
que los contactos de salida son generalmente relés mecánicos.
Relés digitales y relés numéricos
Los relés digitales introdujeron un cambio importante de tecnología. Los circuitos análogos utilizados en los relés
estáticos, fueron remplazados por microprocesadores y microcontroladores, para implementar las funciones de los
relés.
Comparados con los relés estáticos, los relés digitales utilizan conversión análoga/digital (A/D) de todas las variables
análogas medidas.
Los relés numéricos son desarrollos de los relés digitales como resultado del avance de la tecnología. Típicamente
utilizan un procesador de señal digital (DSP), acompañado de un software asociado.
La continua reducción en el costo de los microprocesadores y de los elementos digitales asociados, lleva naturalmente
a que un solo equipo es utilizado para proveer un rango de funciones que anteriormente eran implementadas por
equipos separados.

80. Relé numérico multifuncional
(Sobrecorriente fase/tierra,
medida, recierre, bajo voltaje,
frecuencia, comunicación, etc.)
Relé numérico multifuncional
(Sobrecorriente fase/tierra,
control, medida, recierre, bajo
voltaje, frecuencia,
comunicación, etc.)

81. Protección de Sobrecorriente
Los relés dependen de la variable del sistema de potencia a la cual respondan, como corriente, voltaje, frecuencia, etc.
Por lo tanto, podemos encontrar protecciones de diferentes tipos como son:
Sobrecorriente
Sobre o bajo voltaje
Sobrecorriente direccional
Diferencial de transformador o diferencial de barra
Distancia
Baja o sobre frecuencia
(corriente)
(voltaje)
(corriente, voltaje)
(corriente)
(corriente, voltaje)
(frecuencia, voltaje)
Protección de sobrecorriente es la protección que responde cuando la corriente que circula por ella supera un valor
establecido.
Su funcionamiento es simple ya que su operación depende de dos variables básicas:
−El nivel de corriente mínima de operación (o corriente de pick-up), que es aquel valor que produce el cambio de
estado del relé (arranque).
− La característica de tiempo de operación, es decir la forma en que el relé responde en cuanto al tiempo.

82. Este método se usa preferentemente en líneas radiales o en líneas en anillo, donde la corriente de falla entre las
diversas secciones no difiere mucho. Esta forma de dar selectividad se consigue con relés de tiempo definido.
Tiene la desventaja que el tiempo de despeje de las fallas es cada vez mayor hacia las proximidades de la fuente,
justamente donde el nivel de falla es mayor y donde se debería actuar con más rapidez.
Procedimientos de coordinación
Coordinación por tiempo
En este método se utiliza un intervalo de tiempo (independiente del nivel de corriente de falla) entre cada uno de los
relés que controlan los interruptores del sistema, para asegurar que opere primero el que está más cerca de la falla.

83. Procedimientos de coordinación
Coordinación por corriente
Se basa en el hecho que la corriente de falla varía con la ubicación de ésta debido a la variación de la impedancia entre
la fuente y el punto de falla. Por lo tanto las protecciones se ajustan a valores apropiados de corriente de tal forma que
opere solamente el relé más cercano a la falla. El tiempo de operación de las protecciones se ajusta en forma
instantánea para obtener menores tiempos de despeje de falla.
Este método no es muy práctico en casos donde pueden variar las condiciones de generación, por lo que se podría dar
la situación en que las protecciones operen incorrectamente.
G1
G2
A B
2
1
Fa Fb
Con G1 y G2 en línea:
ZG1  10
ZG 2  15
Z12  5
110
kV
18.3kA
110000V
(10||15)
IFa  10kA
110000V
(10 ||15  5

)
IFb 
Si G1 sale de servicio, entonces:
15

5.5kA
110000V
(15 5

)
IFa 
110000V
 7.3kA IFb 
La corriente de arranque para el relé A se ajustaría al valor mínimo de falla Fa en el elemento protegido (7kA), pero con
este ajuste, para una falla Fb en condiciones de generación máxima, podría operar el relé A simultáneamente y en forma
no selectiva con el relé B.

84. Coordinación por corriente/tiempo
Cada uno de los métodos descritos anteriormente, tiene una desventaja fundamental. Debido a estas desventajas, es
que los relés de sobrecorriente con característica de tiempo inverso han evolucionado.
Con esta característica el tiempo de operación es inversamente proporcional al nivel de corriente de falla, y es una
función tanto del ajuste de tiempo como el de corriente.
Se definen varias curvas de operación dependiendo de la proporcionalidad con la corriente así:
Curva Normal Inversa
Curva Muy Inversa
Curva Extremadamente Inversa
t 
1
Iop

85. CURVAS ESTANDAR INVERSA
0,1
1
10
100
1000
1 10 100 1000
Veces I ajuste
SEGUNDOS
NORMAL INVERSA
MUYINVERSA
EXTREMADAMENTE
INVERSA

86. La norma IEC 60255 define las características inversas de la siguiente manera:
Curva Normal Inversa Curva Muy Inversa
)0.02
1
(I /I
t  TMS
Curva Extremadamente Inversa
0.14 13.5
pu pu
I I 1
t  TMS
80
pu
(I / I )2
1
t  TMS
TMS  Ajuste multiplicador de tiempo o dial y va de 0.05 a 1.0
0,1
1
10
I / I pu  Corriente de falla sobre corriente depick-up
CURVAS NORMAL INVERSA
100
1 100
10
I/Ipu
SEGUNDOS
Dial 0.8
Dial 0.3
Dial 0.1

87. La norma ANSI define las características inversas de la siguiente manera:
Curva Normal Inversa
Curva Muy Inversa





 9
0.0086
)0.02
1
 14TMS 5

 0.0185x


(I/ I

t 
pu
Curva Extremadamente Inversa





 9
2.855  14TMS 5

 0.0712x


(I / I )2
1

t 
pu


9
6.407  14TMS 5

 0.025x


(I / I )2
1

t 

 pu 

TMS  Ajuste multiplicador de tiempo o dial y va de 0.5 a 10.0
Para el caso de relés de sobrecorriente electromecánicos, es usual que el fabricante suministre las curvas de operación
para cada uno de los ajustes de tiempo, teniendo en cuenta que estas curvas no se ajustan exactamente a las
ecuaciones IEC o ANSI.

88. Curvas de operación para un relé electromecánico

89. Definiciones
Es conveniente definir algunos términos que son de uso común en protecciones y que es necesario conocer claramente:
Corriente de arranque o pick-up (I> para fases, Ie> para tierra)
Es la corriente que produce el cambio de estado del relé. En relación a este término existe una diferencia entre los
fabricantes norteamericanos y los europeos. En los relés americanos, el valor de la corriente mínima de operación o
pick-up es igual al valor del tap. En los relés de procedencia europea, estos valores pueden ser diferentes. La corriente
de pick-up es del orden de 1,3 veces el valor del tap.
Las curvas de los relés vienen con el valor de corriente expresado en veces el tap y no en amperios, de modo que sirvan
para cualquier rango de corrientes primarias. También es habitual que las curvas no comiencen en 1 por tap sino en 1,5
veces en el caso de los americanos o 1,3 veces en el caso de los relés ingleses. En los relés de estado sólido es
frecuente que el pick-up sea 1,1 veces el tap y que la curvas comiencen también desde este punto. La razón para esto
es que resulta difícil precisar las curvas para valores de corriente muy cercanos al valor de la toma (tap), de modo que el
fabricante se deja un margen donde no asegura la exactitud de las curvas.
Tap
Es el dispositivo que permite seleccionar la corriente de operación del relé dentro de un rango de tomas o derivaciones
dispuestas para este efecto. Normalmente el valor del tap se designa en amperios y representa el valor de corriente que
haría operar al relé en un tiempo indeterminado (muy largo).

90. Dial de tiempo
Es el ajuste que permite variar las curvas de tiempo de operación del relé. En los relés americanos (norma ANSI) va de
0.5 a 10.0 y en los relés europeos (norma IEC) va de 0.05 a 1.0.
Tiempo de coordinación
Es el intervalo de tiempo que se debe mantener entre las curvas de los relés con el objeto de obtener una operación
secuencial correcta de los interruptores. Su valor depende de factores como: tiempo de apertura de los interruptores,
error de las curvas de operación de los relés, exactitud de los TCs y su posible saturación. Habitualmente se usan
valores aceptables de tiempos de coordinación entre 0.2 y 0.3 segundos.
Normalmente se utiliza un tiempo de coordinación de 0.2 segundos cuando se reunen las mejores condiciones, es decir,
interruptores rápidos, relés de tipo numérico, TCs de buena calidad y una comprobación de los resultados en terreno.
Selectividad con protecciones de tiempo inverso
Para un sistema en alimentación radial, se puede coordinar de acuerdo con las curvas representadas en el gráfico
siguiente:

91. 1000.0 10000.
[pri.A]
1.0000
10.000
[s]
0.100
110.00 kV100.00
Rele 1 Rele 2
Rele 3
I=700.000
pri.A
0.828 s
I=1000.000
pri.A
0.428 s
0.642 s
0.552 s
1.379 s
1.070 s
I=2000.000
pri.A
0.297 s
0.446 s
0.743 s
DIgSILENT
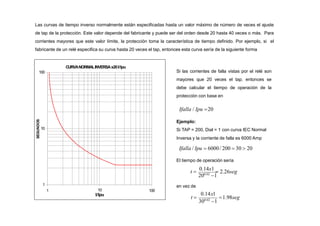
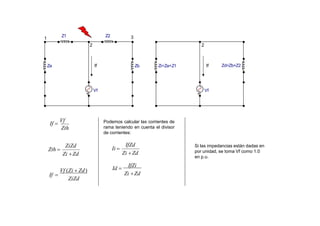
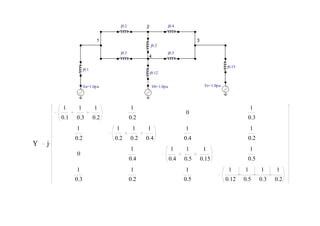
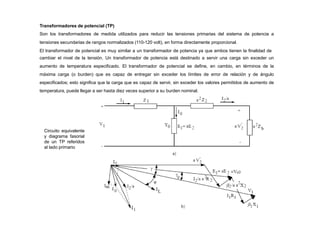
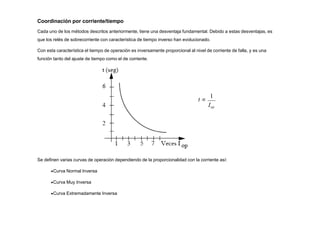
Con estas curvas de coordinación y para el sistema anterior:
Cuando ocurre una falla en 3 (700 Amperios), el relé 3 opera en 0.552 seg, el relé 2 opera en 0.828 seg y el relé 1 opera
en 1.379 seg.
Cuando ocurre una falla en 2 (1000 Amperios), el relé 2 opera en 0.642 seg y el relé 1 opera en 1.070 seg.
Cuando ocurre una falla en 1 (2000 Amperios), el relé 1 opera en 0.743 seg

92. Selectividad con protecciones de tiempo inverso e instantáneas (I>> para fases e Ie>> para
tierra
Se pueden combinar las características de tiempo de operación de los relés para mejorar la selectividad y la estabilidad
del sistema de potencia tal como se muestra en la figura siguiente, especialmente en el caso de líneas largas, donde hay
una apreciable diferencia entre las corrientes de cortocircuito entre dos relés consecutivos. El ajuste de los elementos
instantáneos debe ser tal que no detecte fallas en la barra siguiente a su ubicación, por lo que en general se le da un
margen de un 25 a un 30%, es decir, se multiplica la corriente de falla en la barra siguiente por 1,25 o 1,3.
Si se ajusta el elemento instantáneo para el relé más alejado de la fuente, se escoge entre 6 y 8 veces el tap de fases
para los relés de fases o 10 veces el tap de tierra para los relés de tierra y verificando que este ajuste sea menor que el
50% de la corriente mínima de falla en el punto de ubicación del relé. El tiempo para el elemento instantáneo se ajusta
en 0.05 seg.
Se puede calcular el alcance instantáneo en porcentaje, es decir, la región de la línea protegida que está cubierta por
operación de la sobrecorriente instantánea cuando ocurre una falla en ésta.
local remoto
Instantáneo
Isc  Isc
100
Isclocal  AjusteInstantáneo
%alcance
Ejemplo: Si la corriente para una falla en 3 es de 1000 Amperios y para una falla en 2 es de 2000 Amperios, entonces la
sobrecorriente instantánea del relé 2 se debe ajustar en 1300 Amperios, por lo que el % de alcance instantáneo es:
20001000
100
2000 1300
 70%
Instantáneo
%alcance

93. 1000.0 10000.
[pri.A]
0.100
1.0000
10.000
[s]
0.010
110.00 kV100.00
Rele 1 Rele 2
Rele 3
I=700.000
pri.A
0.828 s
I=1000.000
pri.A
0.050 s
0.050 s 0.050 s
1.379 s
1.070 s
I=2000.000
pri.A
0.050 s
0.050 s
0.050 s
DIgSILENT
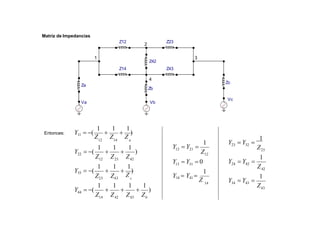
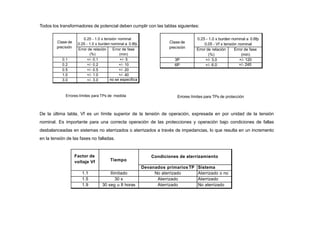
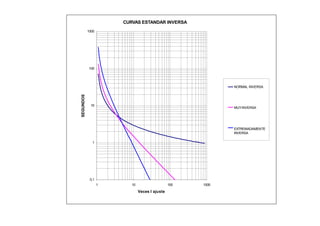
Con estas curvas de coordinación:
Cuando ocurre una falla en 3 (700 Amperios), el relé 3 opera en 0.05 seg, el relé 2 opera en 0.828 seg y el relé 1 opera
en 1.379 seg.
Cuando ocurre una falla en 2 (1000 Amperios), el relé 2 opera en 0.05 seg y el relé 1 opera en 1.070 seg.
Cuando ocurre una falla en 1 (2000 Amperios), el relé 1 opera en 0.05 seg

94. Reglas generales para calcular los ajustes de los relés de sobrecorriente (sistema radial)
Relés de fases
El relé de fases debe detectar fallas por lo menos hasta el extremo final de la sección de circuito siguiente a la
que está protegiendo. Por ejemplo, en la figura siguiente, el relé R1 debe detectar fallas mínimas en el sector del
relé R3.
El tap debe elegirse de modo que el pick-up sea mayor que la corriente máxima de carga y detecte fallas
mínimas en respaldo. Además de esto, en algunos casos, al relé de sobrecorriente se le da el carácter de relé de
sobrecarga eligiendo entonces un ajuste de 1,2 a 1,3 veces la corriente nominal del equipo.
Se ajusta el menor valor entre
1,2 veces la corriente nominal del interruptor
1,2 veces la corriente nominal del TC
1,3 veces la capacidad del equipo protegido
Adicionalmente se debe cumplir que TapR1  TapR2  TapR3
El dial debe elegirse dando el tiempo más corto posible al relé más alejado de la fuente. Si éste no coordina con
otros elementos (fusibles, reconectadores, etc.), debe dársele el dial mínimo permisible. Este dial se recomienda
sea 1 para los americanos y 0,1 para los europeos, pero puede ser hasta 0,5 o 0,05, respectivamente. El resto de
los relés debe coordinarse con los que le anteceden, dándole el tiempo de coordinación más el tiempo del relé
con que se coordina, en el punto que corresponda a la máxima falla. Como tal se considera generalmente una
falla trifásica, con máxima generación justo después de la siguiente barra o el pick-up del instantáneo del relé con
el que se está coordinando. Por ejemplo, en la figura anterior, el dial del relé R2 debe calcularse con el tiempo del
relé R3 más el tiempo de coordinación, con una falla máxima en F (barra siguiente al relé R2). En todo caso, debe
verificarse la coordinación para otro tipo de fallas.

95. Relés de tierra
Para estos relés son válidos los mismos puntos mencionados antes, excepto lo indicado para el tap. En efecto, como
estos relés son alimentados con las corrientes de secuencia cero, las que valen cero para condiciones normales de
operación, puede elegirse un tap de valor inferior a las corrientes normales de carga.
Se ajusta a un valor entre 20-30 % del ajuste del tap de fases y verificando que, para circuitos y líneas de distribución
o transmisión, este valor sea menor o igual que 120 Amperios, que equivale al valor máximo de desbalance permitido
que se puede encontrar en el sistema
Selección de curvas
Para circuitos de distribución (13,8 kV) se escoge la curva muy inversa o extremadamente inversa si se va a
coordinar con fusibles.
Para líneas de distribución, transmisión (  34.5 kV ) se escoge la curva normal inversa
Para transformadores de potencia se escoge la curva normal inversa
Etapas a seguir para calcular los ajustes de relés de sobrecorriente
El cálculo de ajustes de relés de sobrecorriente debe dar finalmente el valor de “tap”, el tipo de curva y el “dial” a
que debe ajustarse cada relé. En los casos que se utilice el elemento instantáneo, también debe entregar el valor
al cual debe ajustarse éste. Para obtener el resultado final es necesario cumplir una serie de etapas previas, que
se resumen a continuación, suponiendo que se dispone del diagrama unifilar del sistema y que se conocen las
relaciones de los TC a usar. También es necesario disponer de las curvas características de los relés (para relés
con curvas no estandar) y graficar en representación log-log para trazar las características de corriente y tiempo.
Las etapas son las siguientes:

96. Dibujar el circuito equivalente por fase (diagrama de impedancias) del sistema eléctrico radial al cual se está aplicando
la protección, indicando los parámetros de cada uno de sus componentes.
Reducir todos los parámetros a una base común. Como se verá posteriormente, todas las corrientes deben estar
referidas a un solo nivel de voltaje, el que conviene que sea el que es común a la mayor parte de los componentes.
Calcular las corrientes nominales de los equipos, reduciéndolas además al nivel de voltaje común.
Calcular las corrientes máximas de falla (con plena generación) y las mínimas (con generación mínima) para cada uno
de los puntos donde se ubican relés.
Calcular los taps de los relés en términos primarios, en función de las corrientes nominales de los equipos y verificando
respaldos para las fallas mínimas.
Calcular los taps en términos secundarios, para lo que basta dividir el valor anterior por la RTC correspondiente.
Reajustar si es necesario los valores de acuerdo con los tap que realmente dispone el relé.
Calcular el ajuste del elemento instantáneo, si procede, con las indicaciones dadas anteriormente (1,3 veces la corriente
máxima de cortocircuito en la barra siguiente).
Reducir todos los valores de tap a términos primarios y expresarlos en una sola base de voltaje. Marcarlos en el gráfico
(log-log) correspondiente.
Calcular los diales de acuerdo a lo indicado teniendo en cuenta los tiempos de coordinación, es decir:
Se conoce la I máxima de falla y el tap ajustado para el relé. Se determina el tiempo deseado de operación del
relé para la I máxima de falla el cual es igual al tiempo de operación de la curva del relé aguas abajo a ese nivel
de falla más el tiempo de coordinación (de 0.2 a 0.3 seg).
Con este tiempo se determina el dial de la curva del relé ya sea en forma analítica, si se conoce la ecuación de la
curva, o en forma gráfica si no se conoce la ecuación de la curva

97. Ejemplo
Supóngase que para este sistema, la corriente de falla máxima en F es de 7000 Amperios y que el relé R3 se ajusta con
un tap de 600 Amperios y el dial mínimo de 0.1 para una curva IEC Normal Inversa.
Para este nivel de corriente el tiempo de operación del relé R3 es:
0.14
3  0.1x2.77 0.27seg
3
(7000 / 600)0.02
1
t  Dial
Para este mismo nivel de falla máxima, el relé R2 debe actuar en un tiempo igual a t3+t coordinación, es decir t2 = 0.27 +
0.2 = 0.47 seg. Supóngase que el tap del relé R2 se ajusta en 650 Amperios y que su curva también es IEC Normal
Inversa, entonces el dial de este relé se determina en forma analítica y se debe ajustar en:
0.14 0.14
0.47(7000 / 650)0.02
1
  0.17
t (I / TAP)0.02
1
Dial2  2 F
Por otro lado, si el relé R2 se ajusta en 650 Amperios y su curva no es estandar, entonces el dial de este relé se
determina en forma gráfica, escogiendo la curva del relé que opere en un tiempo de al menos 0.47 seg para un número
de 7000/650 11 veces el tap

98. La coordinación del relé siguiente se hará a partir de una nueva corriente de falla máxima y con un procedimiento similar
al expuesto. En el caso de utilizar elementos instantáneos, la coordinación se hará a partir del ajuste de corriente de esta
unidad, (el que por supuesto es menor que la corriente de falla máxima) en vez de la corriente de falla máxima.
Es decir, si en el ejemplo anterior al relé R3 se le ajusta el elemento instantáneo en 4800 Amperios, se debe utilizar este
valor en los cálculos del dial y tiempos de operación en vez de la corriente de falla máxima
G2
A B
L L
G1 G2
G2
G1
G2
G1
Z0L  3 / Km
Z1  Z 2  1 / K
m
Z0  Z0 16
Z1  Z1  Z2  Z2 14
2
1
Ejericio: Determinar los ajustes de las protecciones de fases y tierra para el sistema que se muestra a
continuación:
110
kV
G1
C
3
D
4
23
34
Capacidad  460A
RTC  600/5
L  25Km
L 16Km
L1210Km

99. 1 2
Fb
3
Fc
4
Fd
G
110
kV
Fa
14

10

16

25

Z1G  14 ||14  7 Generación máxima (dos generadores enparalelo)
Generación mínima (un generador en fuera de servicio)
Z1G 14
Relés de fases
Se dibuja el diagrama de impedancias en secuencia positiva para el sistema:
14
A B C D
Reducir todos los parámetros a una base común.
En este caso hay un solo nivel de tensión por lo que se puede trabajar con valores directos de los parámetros
Calcular las corrientes nominales de los equipos, reduciéndolas además al nivel de voltaje común.
Para todos los relés, la capacidad de la línea es 460 Amperios y de los TCs es 600 Amperios
Calcular las corrientes máximas de falla (con plena generación) y las mínimas (con generación mínima) para cada uno
de los puntos donde se ubican relés.

100. Relé E ZL ZLeq
Gen Máxima Gen Mínima
Zg If Zg If
A 110.000 10 0 7 15.714 14 7.857
B 110.000 16 10 7 6.471 14 4.583
C 110.000 25 26 7 3.333 14 2.750
D 110.000 51 7 1.897 14 1.692
E
G L
F
Z  Z eq
I 
Calcular los taps de los relés en términos primarios, en función de las corrientes nominales de los equipos y verificando
respaldos para las fallas mínimas.
Se escoge el menor valor entre:
1.2ITC 1.2x600  720A
1.3IL 1.3x460  600A
Se ajusta el tap de todos los relés en 600 Amperios
Calcular los taps en términos secundarios, para lo que basta dividir el valor anterior por la RTC correspondiente.
Reajustar si es necesario los valores de acuerdo con los tap que realmente dispone el relé.
TAPsec  TAPprim / RTC  600/(600 /5)  5AmpSec

101. Calcular el ajuste del elemento instantáneo, si procede, con las indicaciones dadas anteriormente (1,3 veces la corriente
máxima de cortocircuito en la barra siguiente).
Inicialmente no vamos a ajustar el elemento instantáneo
Calcular los diales teniendo en cuenta los tiempos de coordinación (0.2 seg)
Para el relé D (más alejado de la fuente) ajustamos el dial mínimo de 0.05 y vamos a utilizar una curva IEC Normal
Inversa en todos los relés.
Calculamos el tiempo de operación del relé D para una falla máxima en D (1897 Amperios):
El relé C debe coordinar con el relé D en un tiempo mayor que tD+0,20 = 0,30 + 0,20 = 0,50 seg para la falla
máxima en D (1897 Amperios). Calculamos el dial requerido para que el relé C opere en este tiempo:
0.14 0.14
0.50(1897/ 600)0.02
1
  0.09
t (I / TAP)0.02
1
C FD
DialC 
0.14
0.14
 0.14
0.56(3333 / 600)0.02
1

t (I / TAP)0.02
1
B FC
DialB 
D  0.05x6.01 0.30seg
0.14
D
(1897 / 600)0.02
1
t  Dial
Calculamos el tiempo de operación del relé C para una falla máxima en C (3333 Amperios):
C  0.09x4.01 0.36seg
0.14
C
(3333 /600)0.02
1
t  Dial
El relé B debe coordinar con el relé C en un tiempo mayor que tC+0,20 = 0,36 + 0,20 = 0,56 seg para la falla
máxima en C (3333 Amperios). Calculamos el dial requerido para que el relé B opere en este tiempo:

102. 0.14 0.14
  0.21
t (I /TAP)0.02
1 0.60(6471/ 600)0.02
1
A FB
DialA 
Calculamos el tiempo de operación del relé B para una falla máxima en B (6471 Amperios):
B  0.14x2.87 0.40seg
0.14
B
(6471/ 600)0.02
1
t  Dial
El relé A debe coordinar con el relé B en un tiempo mayor que tB+0,20 = 0,40 + 0,20 = 0,60 seg para la falla
máxima en B (6471 Amperios). Calculamos el dial requerido para que el relé A opere en este tiempo:
Calculamos el tiempo de operación del relé A para una falla máxima en A (15714 Amperios):
A  0.21x2.07 0.43seg
0.14
A
(15714 / 600)0.02
1
t  Dial
Relé
TAP
DIAL Curva
A Prim A sec
A 600 5 0,21 IEC Normal Inversa
B 600 5 0,14 IEC Normal Inversa
C 600 5 0,09 IEC Normal Inversa
D 600 5 0,05 IEC Normal Inversa
A continuación se muestra una tabla con los ajustes seleccionados para los relés de sobrecorriente de fases

103. Relé TAP DIAL
If t op t coordinación
Max Min Max Min Max Min
A 600 0,21 1897 1692 1,26 1,40 0,42 0,47
B 600 0,14 1897 1692 0,84 0,94 0,30 0,33
C 600 0,09 1897 1692 0,54 0,60 0,24 0,27
D 600 0,05 1897 1692 0,30 0,33
Para falla en C
Relé TAP DIAL
If t op t coordinación
Max Min Max Min Max Min
A 600 0,21 3333 2750 0,84 0,95 0,28 0,32
B 600 0,14 3333 2750 0,56 0,63 0,20 0,23
C 600 0,09 3333 2750 0,36 0,41
Revisamos los tiempos de operación y coordinación para cada una de las fallas
Para falla en D
Para falla en B
Relé TAP DIAL
If t op t coordinación
Max Min Max Min Max Min
A 600 0,21 6471 4583 0,60 0,71 0,20 0,24
B 600 0,14 6471 4583 0,40 0,47
Se observa que los tiempos de coordinación son mayores que el tiempo establecido de 0.2 seg por lo que la coordinación
es correcta y se garantiza selectividad

104. 1000.0 10000. 100000.
[pri.A]
0.100
1.000
10.000
100.00
[s]
0.010
110.00 kV100.00
Rele A Rele B
Rele C Rele D
I=3333.000
pri.A
0.201 s
0.361 s
0.562 s
0.843 s
I=6471.000
pri.A
0.144 s
0.259 s
0.402 s
0.604 s
I=15714.000
pri.A
0.104 s
0.187 s
0.290 s
0.436 s
I=1897.000
pri.A
0.301 s
0.541 s
0.842 s
1.262 s
DIgSILENT
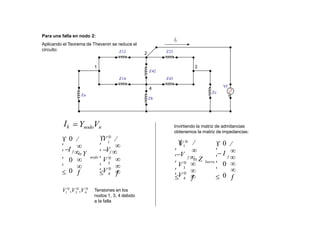
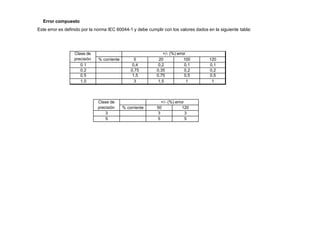
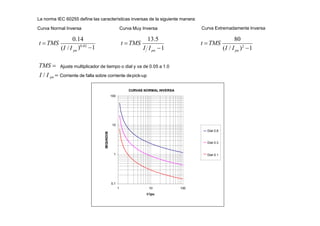
Curvas de coordinación para los relés de fases

105. 1 2
Fb
3
Fc
4
Fd
G
110
kV
Fa
16

30

48

75

Relés de tierra
Se dibuja el diagrama de impedancias en secuencia cero para el sistema:
16
A B C D
Z0G 16 ||16  8 Generación máxima (dos generadores en paralelo)
Z 0G  16 Generación mínima (un generador en fuera de servicio)
Calcular las corrientes máximas de falla (con plena generación) y las mínimas (con generación mínima) para cada uno
de los puntos donde se ubican relés.
F
3E 3E
3E 3E
1 2 0 1 0
  
Z  Z  Z 2Z  Z 2(Z1g  Z1L)  (Z0g  Z0L) 2Z1t  Z0t
I 
Gen Máxima Gen Mínima
Relé E
ZL Sec (+) Sec (0)
If
Sec (+) Sec (0)
If
Sec(+) Sec(0) Z1L Z1g Z1t Z0L Z0g Z0t Z1L Z1g Z1t Z0L Z0g Z0t
A 110.000 10 30 0 7 7 0 8 8 15.000 0 14 14 0 16 16 7.500
B 110.000 16 48 10 7 17 30 8 38 4.583 10 14 24 30 16 46 3.511
C 110.000 25 75 26 7 33 78 8 86 2.171 26 14 40 78 16 94 1.897
D 110.000 51 7 58 153 8 161 1.191 51 14 65 153 16 169 1.104

106. Calcular los taps de los relés en términos primarios, entre un 20 a 30 % del tap de fases y como máximo en 120
Amperios.
0.2TAPfases  TAPtierra  0.3TAPfases 120Amperios
0.2(600)  TAPtierra  0.3(600) 120Amperios
120  TAPtierra 180
TAPtierra 120Amperios
Se ajusta el tap de tierra de todos los relés en 120 Amperios
Calcular los taps en términos secundarios, para lo que basta dividir el valor anterior por la RTC correspondiente.
Reajustar si es necesario los valores de acuerdo con los tap que realmente dispone el relé.
TAPsec  TAPprim / RTC 120/(600/5) 1
Calcular el ajuste del elemento instantáneo, si procede, con las indicaciones dadas anteriormente (1,3 veces la corriente
máxima de cortocircuito en la barra siguiente).
Inicialmente no vamos a ajustar el elemento instantáneo
Calcular los diales teniendo en cuenta los tiempos de coordinación (0.2 seg)
Para el relé D (más alejado de la fuente) ajustamos el dial mínimo de 0.05 y vamos a utilizar una curva IEC Normal
Inversa en todos los relés.
Calculamos el tiempo de operación del relé D para una falla máxima en D (1191 Amperios):

107. El relé C debe coordinar con el relé D en un tiempo mayor que tD+0,20 = 0,15 + 0,20 = 0,35 seg para la falla
máxima en D (1191 Amperios). Calculamos el dial requerido para que el relé C opere en este tiempo:
0.14 0.14
0.35
(1191/120)0.02
1
  0.12
t (I / TAP)0.02
1
C FD
DialC 
0.14 0.14
0.49
(2171/120)0.02
1
  0.21
t (I / TAP)0.02
1
B FC
DialB 
D  0.05x2.98 0.15seg
0.14
D
(1191/120)0.02
1
t  Dial
Calculamos el tiempo de operación del relé C para una falla máxima en C (2171 Amperios):
C  0.12x2.35 0.29seg
0.14
C
(2171/120)0.02
1
t  Dial
El relé B debe coordinar con el relé C en un tiempo mayor que tC+0,20 = 0,29 + 0,20 = 0,49 seg para la falla
máxima en C (2171 Amperios). Calculamos el dial requerido para que el relé B opere en este tiempo:
Calculamos el tiempo de operación del relé B para una falla máxima en B (4583 Amperios):
B  0.21x1.85 0.39seg
0.14
B
(4583 /120)0.02
1
t  Dial

108.   0.32
t (I /TAP)0.02
1 0.59(4583 /120)0.02
1
A FB
DialA 
El relé A debe coordinar con el relé B en un tiempo mayor que tB+0,20 = 0,39 + 0,20 = 0,59 seg para la falla
máxima en B (4583 Amperios). Calculamos el dial requerido para que el relé A opere en este tiempo:
0.14 0.14
Calculamos el tiempo de operación del relé A para una falla máxima en A (15000 Amperios):
A  0.32x1.38 0.44seg
0.14
A
(15000 /120)0.02
1
t  Dial
Relé
TAP
DIAL Curva
A Prim A Sec
A 120 1 0,31 IEC Normal Inversa
B 120 1 0,21 IEC Normal Inversa
C 120 1 0,12 IEC Normal Inversa
D 120 1 0,05 IEC Normal Inversa
A continuación se muestra una tabla con los ajustes seleccionados para los relés de sobrecorriente de tierra

109. Relé TAP DIAL
If t op t coordinación
Max Min Max Min Max Min
A 120 0,32 1191 1104 0,95 0,99 0,33 0,34
B 120 0,21 1191 1104 0,63 0,65 0,27 0,28
C 120 0,12 1191 1104 0,36 0,37 0,21 0,22
D 120 0,05 1191 1104 0,15 0,15
Para falla en C
Relé TAP DIAL
If t op t coordinación
Max Min Max Min Max Min
A 120 0,32 2171 1897 0,75 0,79 0,26 0,27
B 120 0,21 2171 1897 0,49 0,52 0,21 0,22
C 120 0,12 2171 1897 0,28 0,30
Revisamos los tiempos de operación y coordinación para cada una de las fallas
Para falla en D
Para falla en B
Relé TAP DIAL
If t op t coordinación
Max Min Max Min Max Min
A 120 0,32 4583 3511 0,59 0,64 0,20 0,22
B 120 0,21 4583 3511 0,39 0,42
Se observa que los tiempos de coordinación son mayores que el tiempo establecido de 0.2 seg por lo que la coordinación
es correcta y se garantiza selectividad

110. 1000.0 10000. 100000.
[pri.A]
0.100
1.000
10.000
100.00
[s]
0.010
110.00 kV100.00
Rele A ReleB
Rele C ReleD
I=2171.000
pri.A
0.117 s
0.282 s
0.728s
0.493s
I=4583.000
pri.A
0.093 s
0.222 s
0.389 s
0.574 s
I=15000.000
pri.A
0.069 s
0.166 s
0.428s
0.290s
I=1191.000
pri.A
0.149 s
0.358 s
0.924s
0.626s
DIgSILENT
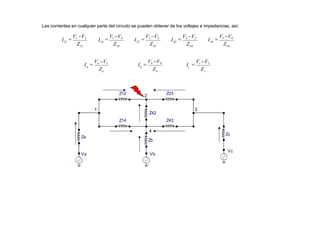
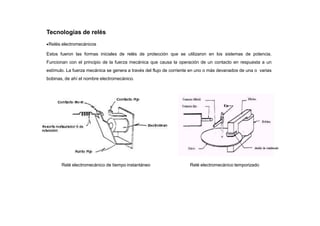
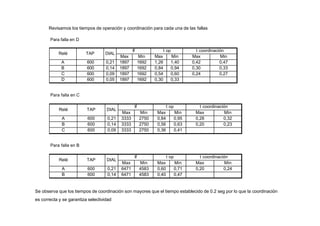
Curvas de coordinación para los relés de tierra

111. Resolver el ejemplo anterior ajustando el elemento instantáneo de fases y tierra.
Relés de fases
Corrientes de corto máximas y mínimas
Relé E ZL ZLeq
Gen Máxima Gen Mínima
Zg If Zg If
A 110.000 10 0 7 15.714 14 7.857
B 110.000 16 10 7 6.471 14 4.583
C 110.000 25 26 7 3.333 14 2.750
D 110.000 51 7 1.897 14 1.692
El tap de fases sigue ajustado en 600 Amperios primarios o 5 Amperios secundarios.
Calculamos el ajuste del elemento instantáneo
Para el relé D, por ser el más alejado de la fuente se ajustaría con el criterio de entre 6 y 8 veces el tap de fases,
es decir entre 3600 y 4800 Amperios primarios, pero estos valores son mayores que las corrientes de falla
máxima y mínima en D por lo que este elemento nunca operaría. Por esta razón, podríamos ajustar el elemento
instantáneo al 80% de la corriente de falla mínima, entonces:
InstantáneaD  I D  0.8IfallaminD  0.8x1692 1350Amp Prim
Calculamos el elemento instantáneo en amperios secundarios:
I D Sec  I  Prim / RTC 1350/(600 /5) 11.25AmpSec

112. Calcular los diales teniendo en cuenta los tiempos de coordinación (0.2 seg) pero no para las corrientes de falla máxima
sino para las corrientes instantáneas ajustadas
Para el relé D (más alejado de la fuente) ajustamos el dial mínimo de 0.05 y vamos a utilizar una curva IEC Normal
Inversa en todos los relés.
Calculamos el tiempo de operación del relé D para su ajuste instantáneo en D (1350 Amperios):
D  0.05x8.56 0.43seg
0.14
D
(1350 / 600)0.02
1
t  Dial
0.14 0.14
0.63(1350 / 600)0.02
1
  0.08
t (I / TAP)0.02
1
C FD
DialC 
Ajustamos el elemento instantáneo para el relé C usando el criterio de 1,3 veces la corriente de falla máxima en la
barra siguiente D (1897 Amperios)
I C 1.3IfallamaxD 1.3x1897  2466Amp Prim
I C Sec  2466 /(600 /5)  20.55AmpSec
El relé C debe coordinar con el relé D en un tiempo mayor que tD+0,20 = 0,43 + 0,20 = 0,63 seg para la corriente
instantánea ajustada en D (1350 Amperios). Calculamos el dial requerido para que el relé C opere en este tiempo:
local remoto
Instantáneo
Isc  Isc
100
Isclocal  AjusteInstantáneo
%alcance
Para el relé C podemos calcular el % de alcance instantáneo tanto para corrientes de falla máximas y mínimas

113. Instantáneo
IscC Max IscDMax
IscC Max  I
F máxima 100
%alcance
33331897
F máxima 100
3333 2466
 60%
%alcanceInstantáneo
Instantáneo
IscC Min IscDMin
IscC Min  I
F mínima 100
%alcance
27501692
%alcance F máxima 100
2750  2466
 27%
Instantáneo
Con generación máxima, la instantánea del relé C cubre hasta el 60% de la línea 3-4
Con generación mínima, la instantánea del relé C cubre solo el 27% de la línea 3-4

114. CURVA ESTANDAR INVERSA
0,1
1
10
100
1000
10 1000
100
Amperios
SEGUNDOS
TAP
TAP
DIAL
DIAL
Consideraciones a tener en cuenta
del TAP
la curva
ocasiona el
en forma
Variar el ajuste
desplazamiento de
horizontal.
Variar el ajuste del DIAL ocasiona el
desplazamiento de la curva en forma vertical.
Por lo tanto, se podría tener una buena
coordinación de varias protecciones de
sobrecorriente con iguales tipos de curva si:
Se tiene el mismo TAP pero distintos ajustes
de DIAL.
Se tiene el mismo DIAL pero distintos ajustes
de TAP.

115. CURVANORMAL INVERSA
1
10
100
10 100 1000 10000
Amperios
SEGUNDOS
TAP200
TAP100
Curvas Normal Inversa con igual DIAL y
diferentes TAPS

116. Las curvas de tiempo inverso normalmente están especificadas hasta un valor máximo de número de veces el ajuste
de tap de la protección. Este valor depende del fabricante y puede ser del orden desde 20 hasta 40 veces o más. Para
corrientes mayores que este valor límite, la protección toma la característica de tiempo definido. Por ejemplo, si el
fabricante de un relé especifica su curva hasta 20 veces el tap, entonces esta curva sería de la siguiente forma
CURVANORMALINVERSAx20I/Ipu
1
10
100
1 100
10
I/Ipu
SEGUNDOS
Si las corrientes de falla vistas por el relé son
mayores que 20 veces el tap, entonces se
debe calcular el tiempo de operación de la
protección con base en
Ifalla / Ipu 20
Ejemplo:
Si TAP = 200, Dial = 1 con curva IEC Normal
Inversa y la corriente de falla es 6000 Amp
Ifalla / Ipu  6000/ 200  30  20
El tiempo de operación sería
200.02
1
t 
0.14x1
 2.26seg
en vez de
0.14x1
1.98seg
300.02
1
t 

117. Protección de Sobrecorriente Direccional
En un sistema de corriente alterna, la corriente es una magnitud cuya dirección sólo puede ser determinada en relación a
otra; se puede solamente afirmar que dos corrientes tienen o no la misma dirección. Es decir, la corriente no tiene una
dirección absoluta. La potencia, en cambio, especialmente la potencia activa, es una magnitud cuya dirección es posible
determinar en forma absoluta, aunque como magnitud de medida para un sistema de protección contra cortocircuitos no
presenta mayores ventajas que la corriente y su aplicación, por otra parte, introduciría enormes complicaciones.
Así, es posible complementar la aplicación de la corriente como magnitud de medida con un relé direccional (o de
potencia) para el caso de una distribución en anillo como el de la figura de abajo. El relé direccional impide la operación
de los relés de sobrecorriente cuando la potencia fluye en dirección opuesta a la sección protegida. Para una falla que
ocurra en el lugar indicado en la figura, operan los relés del circuito fallado, es decir los ubicados en los puntos 3 y 4. El
relé direccional ubicado en 2, en cambio, bloquea el desganche del interruptor respectivo, impidiendo así una
desconexión inadecuada del circuito no fallado. De este modo se obtiene una selectividad que no podría conseguirse
con relés de sobrecorriente.