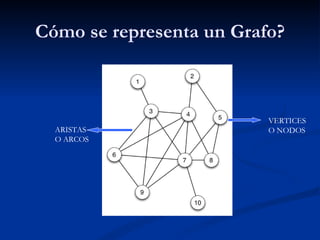
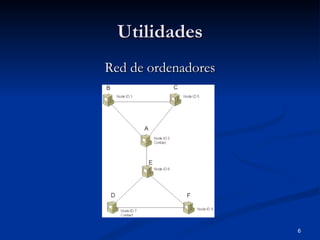
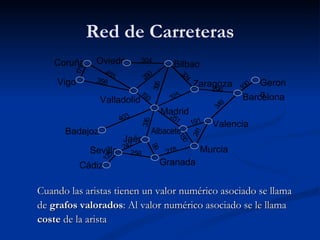
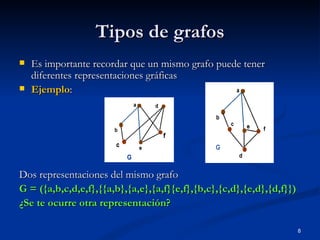
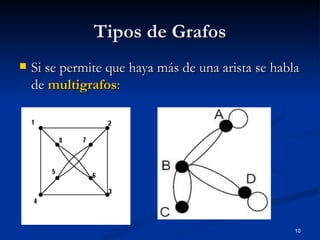
Este documento introduce la teoría de grafos. Explica que un grafo consiste en un conjunto de vértices y aristas que representan la relación entre ellos. Da ejemplos de cómo los grafos pueden modelar sistemas como redes de aeropuertos o carreteras. Describe que los vértices se representan como puntos y las aristas como líneas entre vértices. También cubre conceptos como grafos dirigidos y multigrafos.

1. TEORIA DE GRAFOS Introducción

2. Qué es un Grafo? En Matemática y ciencias de la computación, un grafo (del griego grafos), es una imagen que permiten expresar de una forma visual muy sencilla y efectiva las relaciones que se dan entre elementos de muy diversa índole. Un grafo está formado por dos conjuntos: Un conjunto V de puntos llamados vértices o nodos y un conjunto de pares de vértices que se llaman aristas o arcos y que indican qué nodos están relacionados. De una manera más informal podemos decir que un grafo es un conjunto de nodos con enlaces entre ellos, denominados aristas o arcos

3. Aplicaciones Entre las múltiples aplicaciones que tienen estas estructuras podemos mencionar algunas que sirven para modelar situaciones como: sistemas de aeropuertos Flujo de Tráfico Contactos Responder a las preguntas: ¿Qué tiempo es más corto?, ¿Cuándo es más barato?,¿Qué tarea debo hacer primero?. ¿Están todas las componentes conectadas?.

4. Cómo se representa un Grafo? VERTICES O NODOS ARISTAS O ARCOS

5. Concepto y representación Matemática Un grafo G es un par (V,E) donde: V ={v 1 ,…,v n } es un conjunto de vértices E = {e 1 ,…,e m } es un conjunto de aristas, con cada e k  {v i , v j } , con v i , v j  V , v i ≠ v j Los vértices se representan como puntos y las aristas como líneas entre vértices Ejemplo: G = (V,E) V = {a,b,c,d } E = {{a,b}, {b,c}, {a,c}, {a,d}, {d,b} } Proponer otro recorrido:

6. Utilidades Red de ordenadores

7. Red de Carreteras Cuando las aristas tienen un valor numérico asociado se llama de grafos valorados : Al valor numérico asociado se le llama coste de la arista Madrid Murcia Valencia Granada Sevilla Cádiz Badajoz Vigo Coruña Gerona Barcelona Zaragoza Bilbao Oviedo Valladolid Jaén 2 5 1 1 5 0 4 0 3 2 4 1 3 4 9 1 9 1 9 9 1 2 5 3 5 6 3 0 4 3 9 5 4 5 5 1 7 1 2 8 0 1 9 3 3 2 4 3 2 5 2 9 6 1 0 0 3 3 5 2 7 8 2 4 2 2 5 6 Albacete

8. Tipos de grafos Es importante recordar que un mismo grafo puede tener diferentes representaciones gráficas Ejemplo : Dos representaciones del mismo grafo G = ({a,b,c,d,e,f},{{a,b},{a,e},{a,f}{e,f},{b,c},{c,d},{e,d},{d,f}}) ¿Se te ocurre otra representación?

9. Tipos de Grafos Si el orden influye en la aristas se habla de grafos dirigidos : En este caso a las aristas se les llama arcos y se representan como pares para indicar el orden: V = { a,b,c,d,e} E ={(e,a), (a,b), (b,a), (d,a), (c,d), (d,c),(b,c),(c,b) }

10. Tipos de Grafos Si se permite que haya más de una arista se habla de multigrafos :

11. Conclusiones