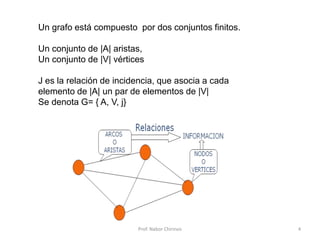
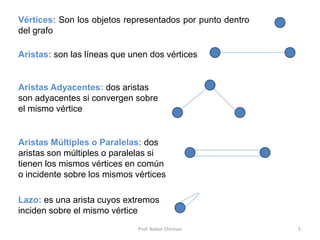
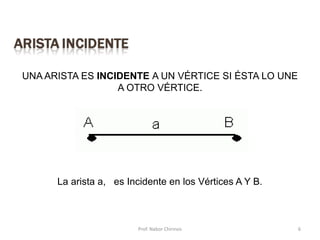
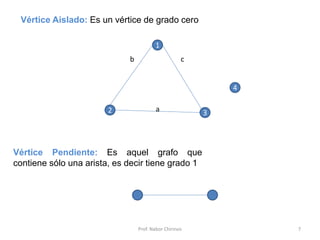
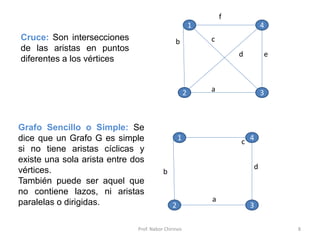
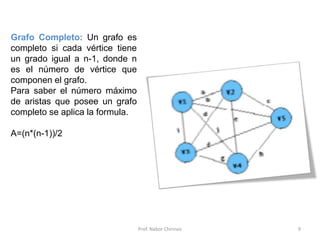
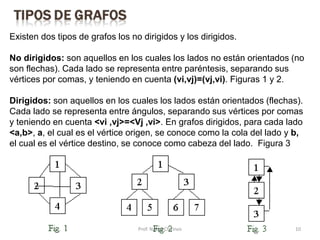
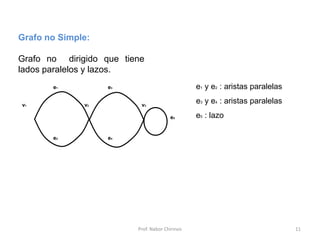
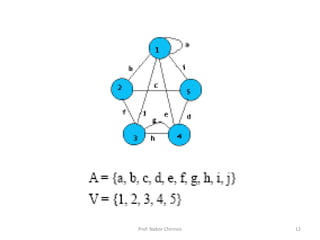
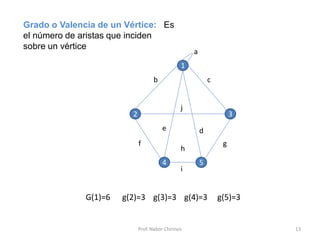
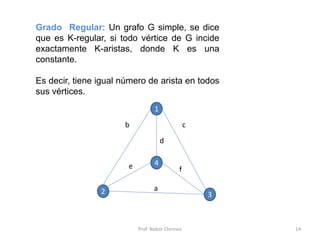
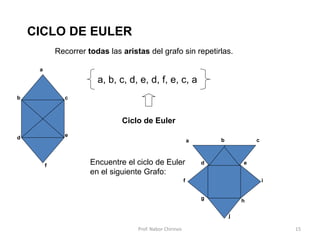
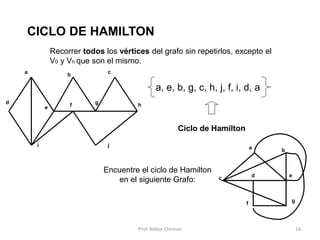
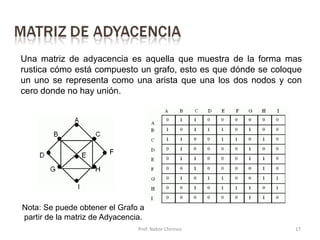
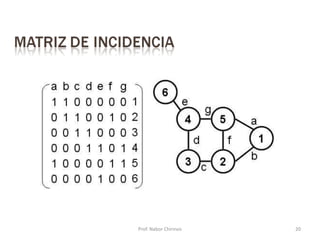
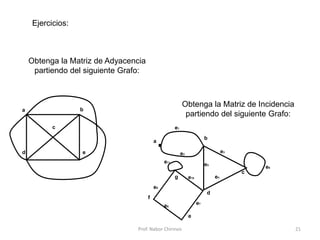
Este documento presenta una introducción a los grafos y sus aplicaciones más importantes. Explica conceptos básicos como vértices, aristas, grado de un vértice, ciclos de Euler y Hamilton, y diferentes tipos de grafos. También describe formas de representar grafos como matrices de adyacencia y de incidencia.

1. 1Ing. Nabor Chirinos

2. 2Prof. Nabor Chirinos
LAS APLICACIONES MÁS IMPORTANTES DE LOS GRAFOS
SON LAS SIGUIENTES:
· RUTAS ENTRE CIUDADES.
· DETERMINAR TIEMPOS MÁXIMOS Y MÍNIMOS EN UN
PROCESO.
· FLUJO Y CONTROL EN UN PROGRAMA.

3. Prof. Nabor Chirinos 3
Grafo:
Para las matemáticas y las ciencias de la computación, un
grafo es el principal objeto de estudio de la teoría de grafos.
De esta forma, un grafo se representa gráficamente como un
conjunto de puntos (llamados vértices o nodos), unidos por
líneas (aristas). Los grafos permiten estudiar las
interrelaciones entre unidades que se encuentran en
interacción.
Son diagramas que si se interpretan
en forma adecuada proporcionan
información, como por ejemplo los
mapas, diagramas de circuitos o de
flujos, entre otros

4. Prof. Nabor Chirinos 4
Un grafo está compuesto por dos conjuntos finitos.
Un conjunto de |A| aristas,
Un conjunto de |V| vértices
J es la relación de incidencia, que asocia a cada
elemento de |A| un par de elementos de |V|
Se denota G= { A, V, j}

5. Prof. Nabor Chirinos 5
Vértices: Son los objetos representados por punto dentro
del grafo
Aristas: son las líneas que unen dos vértices
Aristas Adyacentes: dos aristas
son adyacentes si convergen sobre
el mismo vértice
Aristas Múltiples o Paralelas: dos
aristas son múltiples o paralelas si
tienen los mismos vértices en común
o incidente sobre los mismos vértices
Lazo: es una arista cuyos extremos
inciden sobre el mismo vértice

6. Prof. Nabor Chirinos 6
UNA ARISTA ES INCIDENTE A UN VÉRTICE SI ÉSTA LO UNE
A OTRO VÉRTICE.
La arista a, es Incidente en los Vértices A Y B.

7. Prof. Nabor Chirinos 7
Vértice Aislado: Es un vértice de grado cero
4
1
2 3
b
a
c
Vértice Pendiente: Es aquel grafo que
contiene sólo una arista, es decir tiene grado 1

8. Prof. Nabor Chirinos 8
Cruce: Son intersecciones
de las aristas en puntos
diferentes a los vértices
Grafo Sencillo o Simple: Se
dice que un Grafo G es simple
si no tiene aristas cíclicas y
existe una sola arista entre dos
vértices.
También puede ser aquel que
no contiene lazos, ni aristas
paralelas o dirigidas.
41
2 3
b
a
c
d e
f
41
2 3
b
a
d
c

9. Prof. Nabor Chirinos 9
Grafo Completo: Un grafo es
completo si cada vértice tiene
un grado igual a n-1, donde n
es el número de vértice que
componen el grafo.
Para saber el número máximo
de aristas que posee un grafo
completo se aplica la formula.
A=(n*(n-1))/2

10. Prof. Nabor Chirinos 10
Existen dos tipos de grafos los no dirigidos y los dirigidos.
No dirigidos: son aquellos en los cuales los lados no están orientados (no
son flechas). Cada lado se representa entre paréntesis, separando sus
vértices por comas, y teniendo en cuenta (vi,vj)=(vj,vi). Figuras 1 y 2.
Dirigidos: son aquellos en los cuales los lados están orientados (flechas).
Cada lado se representa entre ángulos, separando sus vértices por comas
y teniendo en cuenta <vi ,vj>=<Vj ,vi>. En grafos dirigidos, para cada lado
<a,b>, a, el cual es el vértice origen, se conoce como la cola del lado y b,
el cual es el vértice destino, se conoce como cabeza del lado. Figura 3

11. Prof. Nabor Chirinos 11
Grafo no Simple:
Grafo no dirigido que tiene
lados paralelos y lazos.
v1 v2 v3
e1
e2
e3
e4
e5
e1 y e2 : aristas paralelas
e3 y e4 : aristas paralelas
e5 : lazo

12. Prof. Nabor Chirinos 12

13. Prof. Nabor Chirinos 13
Grado o Valencia de un Vértice: Es
el número de aristas que inciden
sobre un vértice
1
2 3
4 5
a
b
e d
c
f g
h
i
j
G(1)=6 g(2)=3 g(3)=3 g(4)=3 g(5)=3

14. Prof. Nabor Chirinos 14
Grado Regular: Un grafo G simple, se dice
que es K-regular, si todo vértice de G incide
exactamente K-aristas, donde K es una
constante.
Es decir, tiene igual número de arista en todos
sus vértices.
4
1
2 3
b
a
c
d
e f

15. Prof. Nabor Chirinos 15
CICLO DE EULER
Recorrer todas las aristas del grafo sin repetirlas.
a
b c
d e
f
a, b, c, d, e, d, f, e, c, a
Ciclo de Euler
Encuentre el ciclo de Euler
en el siguiente Grafo:
a b c
d e
f
g h
i
j

16. Prof. Nabor Chirinos 16
CICLO DE HAMILTON
Recorrer todos los vértices del grafo sin repetirlos, excepto el
V0 y Vn que son el mismo.
a, e, b, g, c, h, j, f, i, d, a
Ciclo de Hamilton
Encuentre el ciclo de Hamilton
en el siguiente Grafo:
a b c
d
e f g h
i j a b
c d e
f g

17. Prof. Nabor Chirinos 17
Una matriz de adyacencia es aquella que muestra de la forma mas
rustica cómo está compuesto un grafo, esto es que dónde se coloque
un uno se representa como una arista que una los dos nodos y con
cero donde no hay unión.
Nota: Se puede obtener el Grafo a
partir de la matriz de Adyacencia.

18. Prof. Nabor Chirinos 18
•ES CUADRADA Y SIMÉTRICA
•LA SUMA DE CADA FILA (O COLUMNA) ES EL GRADO DEL
VÉRTICE CORRESPONDIENTE
•LA DIAGONAL ES NULA

19. Prof. Nabor Chirinos 19
Una matriz que está compuesta por unos y ceros, en la que se
representan los nodos unidos por las aristas. Cada arista une
dos y nada más que dos nodos.
En general, las matrices de incidencia no son usadas
computacionalmente, pero sirven como ayuda conceptual.
PROPIEDADES:
•No tiene por qué ser ni cuadrada ni simétrica

20. Prof. Nabor Chirinos 20

21. Prof. Nabor Chirinos 21
Obtenga la Matriz de Adyacencia
partiendo del siguiente Grafo:
Obtenga la Matriz de Incidencia
partiendo del siguiente Grafo:
a b
c
d e
.a
b
c
d
e
f
g
e1
e2
e3
e4
e5
e6
e7
e8
e9
e10
e11
Ejercicios: