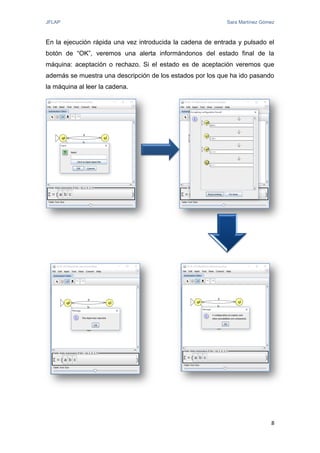
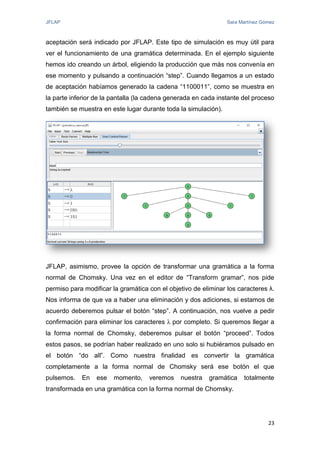
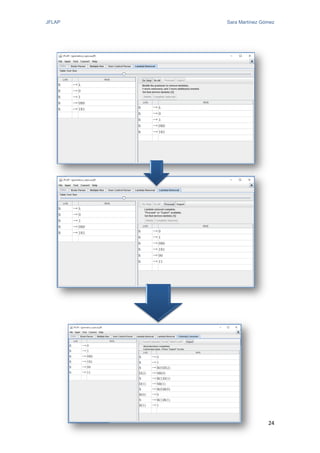
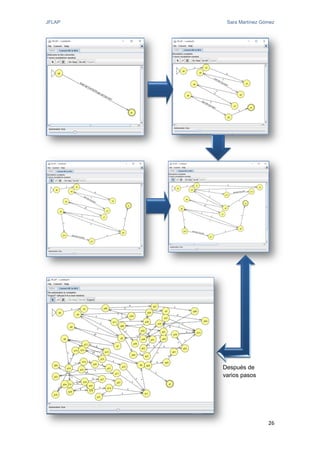
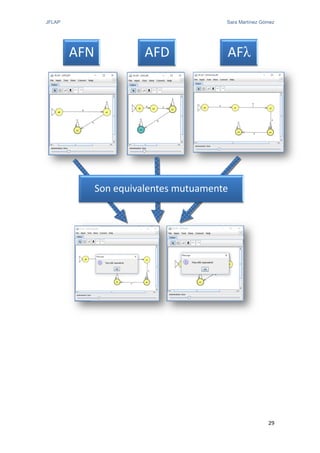
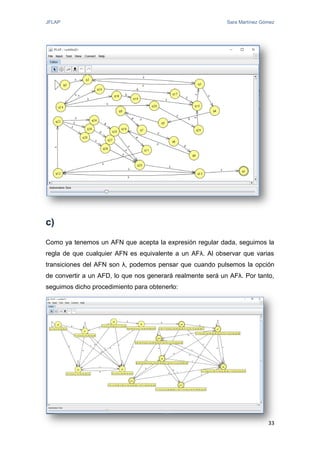
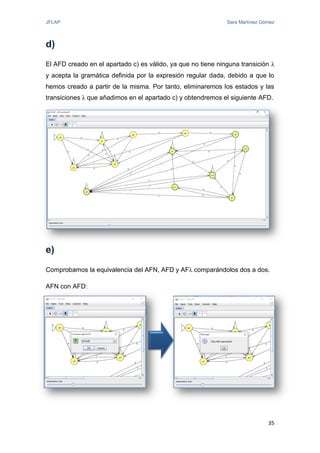
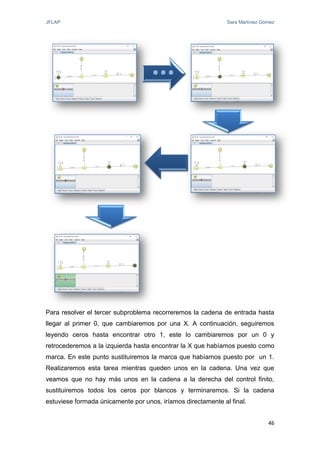
El documento proporciona una introducción a JFLAP, una herramienta para crear y simular autómatas y gramáticas. Explica la historia de JFLAP, los diferentes tipos de autómatas que puede simular (autómatas finitos, máquinas de Mealy, máquinas de Moore, máquinas de Turing) y sus modos de simulación. También cubre conceptos como gramáticas y expresiones regulares que JFLAP permite trabajar.