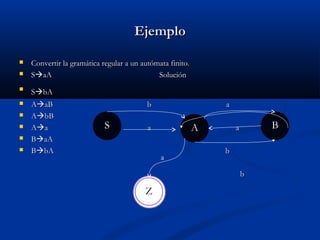
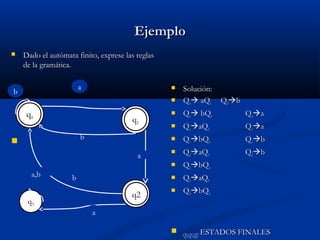
Este documento presenta una introducción a los conceptos básicos de las gramáticas formales y los lenguajes formales. Define formalmente una gramática y sus componentes. Explica los conceptos de reglas de producción, derivación, lenguaje generado y analisis gramatical. Incluye varios ejemplos para ilustrar estos conceptos.

1. UNIVERSIDAD PERUANA DE
CIENCIAS E INFORMÁTICA
Matemática Discreta
Introducción a los Lenguajes
Formales
Profesor: Pascual Fermín
Onofre Mayta

2. GRAMÁTICA
Una gramática es un modelo matemático que se utiliza para especificar la
sintaxis de un lenguaje. Se define formalmente de la siguiente forma:
G = { V N , VT , S , P }
donde
V : Es un conjunto finito de símbolos no terminales de un vocabulario
N
V, que puede sustituirse por otros símbolos
V : es un conjunto finito de símbolos terminales de V, que no pueden
T
sustituirse por otros símbolos.
S : Es un símbolo especial de V que se denomina como el símbolo de
N
inicio, a partir del cual siempre se empieza a construir palabras.
P : Es el conjunto de reglas de producción (reglas gramaticales) cada uno
de la forma w0  w1, lo cual significa que w0 puede sustituirse por w1, w0
debe contener al menos un símbolo no terminal en tanto que w1 puede
consistir en cualquier combinación de símbolos no terminales y
terminales.
Las reglas de produccion se escriben por ejemplo:
SaAB , A Bba (esto quiere decir, S deriva en aAB)

3. Ejemplo. Sea una gramática G =

{ VT , VN , S , R }, donde
ST = {Juan, Ana, corre, come, salta, rápido, lento}

SN = {oración, sujeto, predicado, verbo, adverbio}

S = oración
R1 : oración → sujeto predicado


R2 : predicado → verbo adverbio

R3 : sujeto → Juan

R4 : sujeto → Ana

R5 : verbo → corre

R6 : verbo → come

R7 : verbo → salta

R8 : adverbio → rápido

R9 : adverbio → lento

4. Ejemplo de una cadena:
¿Soporta esta gramática Ana corre rapido?
oración ⇒ sujeto predicado
⇒ Ana predicado
⇒ Ana verbo adverbio
⇒ Ana corre adverbio
⇒ Ana corre rápido
Entonces:
S ⇒ Ana corre rápido,
En consecuencia, Ana corre rápido ∈ L(G)


5. Ejemplo. Encuentre el lenguaje generado por la
gramática
G = {(S,A,B) , (a,b) ,S , P}
donde P es el conjunto de producciones:
S→AB , S→AA , A→aB , A →ab , B→b
Solución
S → AB → aBB → abB →abb
ó
S →AA →aBA →abA →abab
ó
S →AA →aBaB →abaB →abab
En consecuencia,
L(G)={abb,abab}

6. Ejemplo. Encuentre el lenguaje generado por la
gramática G={(S),(0,1),S, P}, donde P consiste en
la producción:
{ S →11S , S →0 }
Solución
S →0 ó S →11S →110 ó también
S →11S →1111S →11110 ó etcétera
En consecuencia,
L(G)={12n0 ; n>= 0 }

7. Derivación mas a la izquierda
Sea la gramática G ={(S,A),(a,b),S,P}, donde P consiste
en las producciones
{S→ aAS, S →a, A →SbA, A →ba}.
Genere la cadena aabbaa
Solución.
S → aAS →aSbAS(La A mas a la izquierda se sustituye
por SbA)
→ aabAS(la S más a la izquierda se sustituye
por a)
→aabbaS (la A más a la izquierda se sustituye
por ba)
→aabbaa (S se sustituye por a)

8. Derivación mas a la derecha
Si G = {(S,A),(a,b),S,P}, donde P consiste en las
producciones
{S→ aAS, S →a, A →SbA, A →ba},
genere la cadena aabbaa
Solución
S → aAS
→aAa(La S mas a la derecha se sustituye por a)
→ aSbAa(la A más a la derecha se sustituye por SbA)
→aSbbaa (la A más a la derecha se sustituye por ba)
→aabbaa (S máa a la derecha se sustituye por a)

9. ANALISIS GRAMATICAL DE
ARRIBA HACIA ABAJO
Determine el análisis gramatical de arriba hacia abajo para determinar
si la cadena ‘abab’ pertenece a la gramática; se conoce:
Si G={(S,A,B),(a,b),S,P}, y P consiste en las producciones
{S→ AB, AB →BA, A →aA, B →Bb, A →a,B →b}
Entonces si derivamos
S → AB →aAB → aABb →aBAb →abAb →abab

10. ANALISIS GRAMATICAL DE
ABAJO HACIA ARRIBA
Determine el análisis gramatical de arriba hacia abajo para determinar
si la cadena ‘abab’ pertenece a la gramática; se conoce:
Si G={(S,A,B),(a,b),S,P}, y P consiste en las producciones
{S→ AB, AB →BA , A →aA , B →Bb , A →a, B →b}
Entonces si derivamos de abajo hacia arriba , esto es partiendo de la
Cadena:
abab ← aBab ← aBAb ← aABb ← ABb ←AB
De manera la cadena ‘abab’ pertenece a L(G)

11. Ejemplo.
Crear las reglas de producción
que reconozca: double a;
Solución.
<VAR><TIPO> <id>;
<tipo> double
<id> a
<VAR>
<TIPO>
double
<id>
a
;

12. <var>
Ejemplo.
Crear las reglas de producción
que reconozca: int a,b,c;
<var><tipo><vars>;
<vars><unaV>
<vars><unaV>,<vars>
<unaV> id
<tipo> int
<tipo> double
<id> a|b|c
<tipo>
<vars>
;
<int> <unaV> ,<vars>
<id>
<unaV>,<vars>
a
id
<unaV>
b
id
c

13. Tipos de Gramática
Una gramática es de tipo 0 si no tiene restricciones en las producciones.
Ejemplo : S aAB, AB a , A b, B AB
 Una gramática “G” es de tipo 1 si cualquier producción es de la forma αβ
donde | α | <=| β | (Las || indican cardinalidad) , o de la forma
α  ‫ ג )ג‬es cadena vacía)
Ejemplo: S aAB, AB bB, B b, A aB
 Una gramática “G” es de tipo 2 si cualquier producción es de la forma A  β
donde
el miembro izquierdo A es un no terminal.
Ejemplo: S aA, A aAB, B b, A a
 Una gramática “G” es de tipo 3 si toda producción es de la forma A a o
AaB, Es decir donde el miembro izquierdo A es un solo no terminal y el
lado derecho es un solo terminal , o un terminal seguido por un no
terminal , o de la forma S ‫ג‬
S aB, B bA, B b, B a, A aB, A a

14. TIPOS DE GRAMATICA(Observación)








Las gramáticas constituyen una jerarquía, toda gramática toda gramática tipo 3 es de
tipo 2, toda gramática de tipo 2 es de tipo 1 y toda gramática tipo 1 es de tipo 0.
A) Una gramática es sensible al contexto si las producciones son de la forma
αA α‘ α β α’
B) Una gramática es libre de contexto si las producciones son de la forma A  β
La expresión libre del contexto proviene del hecho de que es posible sustituir la
variable A por β sin tomar en cuenta donde aparece A.
C) Una gramática es regular si las producciones son de la forma:
Aa, A a B, S ‫ג‬
Observación:
 Una gramática libre del contexto es lo mismo que una gramática tipo 2, una
gramática regular es similar al tipo 3.

15. FORMA DE BACKUS_NAUR

Hay otra notación que se denomina forma de BACKUS NAUR, que algunas
veces se usa para describir las producciones de una gramática libre de
contexto (tipo 2) específicamente.

i) “::=“ se usa en lugar de “”

ii) Cualquier no terminal se escribe entre paréntesis < >.

iii) Toda la producción con el mismo miembro izquierdo no terminal se
combinan en una proposición con todos los miembros derechos enumerados
a la derecha de “::=” separadas por barra verticales.

Por ejemplo:
A aB
, Ab
, ABC
Se combinan en BACKUS NAUR como:
A::= a<B> |b| <B><C>




16. Ejemplo
Sea una gramática G = (ST,SN,n0,R), donde:

ST= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ., +, -}

SN= {real, frac, ent, dig, sign}

n0= real

R1:<real>::=<ent>|<frac>|<ent><frac>|<sign><real>

R2: <frac> ::= . <ent>

R3: <ent> ::= <dig>| <dig><ent>

R4: <dig> ::= 0|1|2|3|4|5|6|7|8|9

R5: <sign> ::= +| -

17. Ejemplo:











Verificar si 21.07 ∈ L(G)
real ⇒ ent frac
⇒ dig ent frac
⇒ dig dig frac
⇒ dig dig . ent
⇒ dig dig . dig ent
⇒ dig dig . dig dig
⇒ 2 dig . dig dig
⇒* 2 1 . 0 7
Entonces:
n0 ⇒* 2 1 . 0 7 ∈ L(G)

18. Ambigüedad en GLC


Una GLC es ambigua si existe una cadena w ∈ L(G) que tiene más de una derivación
por la izquierda o más de una derivación por la derecha o si tiene dos o más árboles
de derivación. En caso de que toda cadena w ∈ L(G) tenga un único árbol de
derivación, la gramática es no ambigua.
Ejemplo: la gramática S → aS | Sa | a es ambigua porque aa tiene dos derivaciones
por la izquierda

S  aS  aa
S  Sa  aa
S
a
S
S
S
a
a
a
Esta gramática genera el lenguaje a+ que también es el lenguaje generado por la
gramática no ambigua S → aS | a.
18

19. Otro ejemplo:

a gramática para expresiones aritméticas sobre las variables x y y:
 E→E+E
 E→E∗E
 E→x
 E→y
es ambigua porque tiene dos árboles de derivación:
E
E
E
x
+
E
∗
E
E
E
+
E
x
x
E
*
y
y
19
E
x

20. AUTOMATAS Y GRAMATICAS

Decimos que una gramática G es equivalente a un automata M(G≡M) si el lenguaje
reconocido por el automata es igual al lenguaje generado por la gramática, es decir si
L(G)=L(M)
Ejemplo
 Sea la gramática G con V={a,b,c,d}, ∑={a,b}, variables={S,A}, el símbolo inicial es S
y la regla de producción son:
 S aS/aA
AbA/b
a
b
 M:
S
Z
A b
a

Observe que G y M reconocen a+ b+

21. Ejemplo


Convertir la gramática regular a un autómata finito.
SaA
Solución

SbA

AaB
AbB
Aa
BaA
BbA




b
S
a
A
a
a
B
a
b
b
Z

22. Ejemplo

Dado el autómata finito, exprese las reglas
de la gramática.
a
b


Solución:
Q0 aQ1
Q0b
a
a,b
b
q2
q2
q3
Q0a

Q1aQ2
Q1a
Q1bQ0
Q1b

Q2aQ3
Q2b
Q2bQ0

b

Q0 bQ0

q1


q0
Q3aQ3

Q3bQ3

Q0,Q1,Q2 ESTADOS FINALES
a