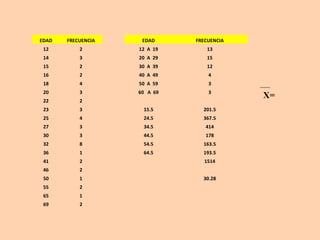
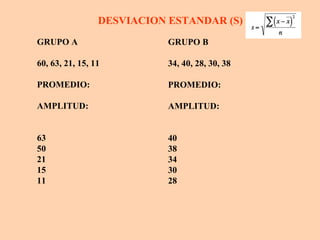
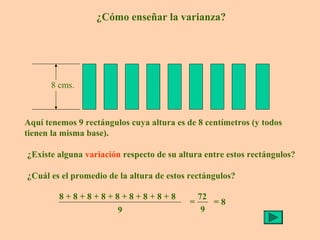
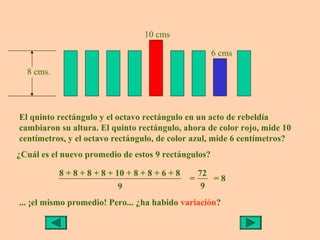
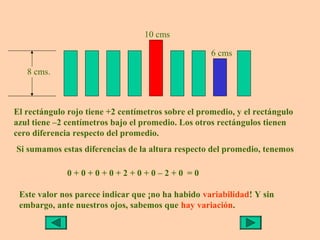
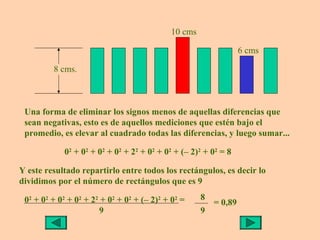
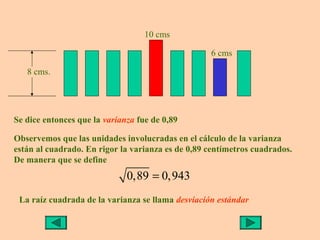
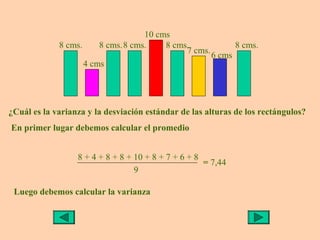
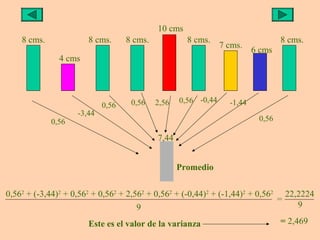
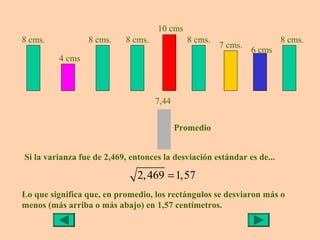
Este documento presenta información sobre medidas de dispersión como la desviación estándar y la varianza. Explica cómo calcular la media aritmética, desviación estándar y varianza para datos agrupados o no agrupados. También utiliza ejemplos de rectángulos de diferentes alturas para ilustrar de manera visual el cálculo y significado de la varianza y desviación estándar.

1. MEDIDAS DE DISPERSION
Dr. Héctor Martínez Alday MSP

2. PROMEDIO O MEDIA ARITMETICA
DATOS AGRUPADOS

3. PASOS
ENCONTRAR EL PUNTO MEDIO DEL INTERVALO
MULTIPLICAR ESE PUNTO POR LA FRECUENCIA
DEL INTERVALO
SUMAR LOS PRODUCTOS
DIVIDIR ENTRE (N)

4. EDAD FRECUENCIA EDAD FRECUENCIA
12 2 12 A 19 13
14 3 20 A 29 15
15 2 30 A 39 12
16 2 40 A 49 4
18 4 50 A 59 3
20 3 60 A 69 3
X=
22 2
23 3 15.5 201.5
25 4 24.5 367.5
27 3 34.5 414
30 3 44.5 178
32 8 54.5 163.5
36 1 64.5 193.5
41 2 1514
46 2
50 1 30.28
55 2
65 1
69 2

5. PASOS
HALLAR LA MEDIA ARITMETICA
HALLAR LOS DESVIOS (d) RESTANDO A CADA VALOR LA MEDIA
ELEVAR AL CUADRADO CADA VALORDE LOS DESVIOS
SUMAR LOS DESVIOS AL CUADRADO (d)2
DIVIDIR LA SUMA POR EL NUMERO
OBTENER LA RAIZ CUADRADA.

6. DESVIACION ESTANDAR (S)
GRUPO A GRUPO B
60, 63, 21, 15, 11 34, 40, 28, 30, 38
PROMEDIO: PROMEDIO:
AMPLITUD: AMPLITUD:
63 40
50 38
21 34
15 30
11 28

7. ¿Cómo enseñar la varianza?
8 cms.
Aquí tenemos 9 rectángulos cuya altura es de 8 centímetros (y todos
tienen la misma base).
¿Existe alguna variación respecto de su altura entre estos rectángulos?
¿Cuál es el promedio de la altura de estos rectángulos?
8+8+8+8+8+8+8+8+8 72
= =8
9 9

8. 10 cms
6 cms
8 cms.
El quinto rectángulo y el octavo rectángulo en un acto de rebeldía
cambiaron su altura. El quinto rectángulo, ahora de color rojo, mide 10
centímetros, y el octavo rectángulo, de color azul, mide 6 centímetros?
¿Cuál es el nuevo promedio de estos 9 rectángulos?
8 + 8 + 8 + 8 + 10 + 8 + 8 + 6 + 8 72
= =8
9 9
... ¡el mismo promedio! Pero... ¿ha habido variación?

9. 10 cms
6 cms
8 cms.
El rectángulo rojo tiene +2 centímetros sobre el promedio, y el rectángulo
azul tiene –2 centímetros bajo el promedio. Los otros rectángulos tienen
cero diferencia respecto del promedio.
Si sumamos estas diferencias de la altura respecto del promedio, tenemos
0+0+0+0+2+0+0–2+0 =0
Este valor nos parece indicar que ¡no ha habido variabilidad! Y sin
embargo, ante nuestros ojos, sabemos que hay variación.

10. 10 cms
6 cms
8 cms.
Una forma de eliminar los signos menos de aquellas diferencias que
sean negativas, esto es de aquellos mediciones que estén bajo el
promedio, es elevar al cuadrado todas las diferencias, y luego sumar...
02 + 02 + 02 + 02 + 22 + 02 + 02 + (– 2)2 + 02 = 8
Y este resultado repartirlo entre todos los rectángulos, es decir lo
dividimos por el número de rectángulos que es 9
02 + 02 + 02 + 02 + 22 + 02 + 02 + (– 2)2 + 02 = 8
= 0,89
9 9

11. 10 cms
6 cms
8 cms.
Se dice entonces que la varianza fue de 0,89
Observemos que las unidades involucradas en el cálculo de la varianza
están al cuadrado. En rigor la varianza es de 0,89 centímetros cuadrados.
De manera que se define
0,89 = 0,943
La raíz cuadrada de la varianza se llama desviación estándar

12. 10 cms
6 cms
8 cms.
Que la desviación estándar haya sido de 0,943 significa que en promedio la
altura de los rectángulos variaron (ya sea aumentando, ya sea
disminuyendo) en 0,943 centímetros.
Es claro que esta situación es “en promedio”, puesto que sabemos que
los causantes de la variación fueron los rectángulos quinto y octavo.
Esta variación hace repartir la “culpa” a todos los demás rectángulos
que se “portaron bien”.
La desviación estándar mide la dispersión de los datos respecto del
promedio

13. 10 cms
8 cms. 8 cms.8 cms. 8 cms. 8 cms.
7 cms.
6 cms
4 cms
¿Cuál es la varianza y la desviación estándar de las alturas de los rectángulos?
En primer lugar debemos calcular el promedio
8 + 4 + 8 + 8 + 10 + 8 + 7 + 6 + 8
= 7,44
9
Luego debemos calcular la varianza

14. 10 cms
8 cms. 8 cms. 8 cms. 8 cms. 8 cms.
7 cms.
6 cms
4 cms
0,56 2,56 0,56 -0,44 -1,44
0,56
-3,44
0,56 0,56
7,44
Promedio
0,562 + (-3,44)2 + 0,562 + 0,562 + 2,562 + 0,562 + (-0,44)2 + (-1,44)2 + 0,562 22,2224
=
9 9
Este es el valor de la varianza = 2,469

15. 10 cms
8 cms. 8 cms. 8 cms. 8 cms. 8 cms.
7 cms.
6 cms
4 cms
7,44
Promedio
Si la varianza fue de 2,469, entonces la desviación estándar es de...
2, 469 = 1,57
Lo que significa que, en promedio, los rectángulos se desviaron más o
menos (más arriba o más abajo) en 1,57 centímetros.

16. Para que el alumno aprenda la varianza necesariamente debe saber:
•Sumar
•Restar
•Multiplicar
•Dividir
•Potencia de orden 2
•Raíz cuadrada
Y es claro que esto no es suficiente (salvo que queramos que aprenda de
memoria los cálculos). Necesitamos estimular su imaginación para que
“vea” la variabilidad existente en la naturaleza.
Entregue una lista de fenómenos en que un mismo atributo tenga
variabilidad si se mide este atributo a un número de individuos u objetos.

17. He aquí unos sencillos ejemplos:
TAREA
•La altura de los estudiantes del curso.
•La nota obtenida en Lenguaje de los estudiantes del curso.
•El valor del dólar diario en pesos en el transcurso de una semana.
•El consumo mensual de agua potable durante 5 meses en la casa.
•El número de accidentes de tránsito diarios durante un mes en la
ciudad.
•Las faltas de ortografía en el dictado de un pequeño texto que comete
cada estudiante del curso.
Pida al estudiante que de ejemplos, de tal forma que pueda calcular
el promedio, la varianza y la desviación estándar.