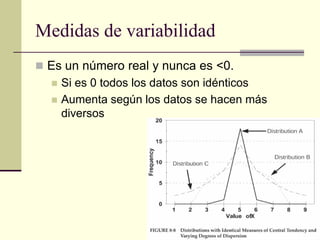
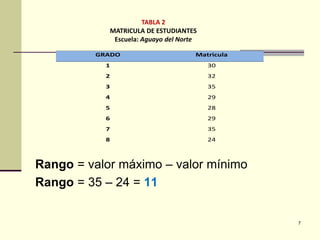
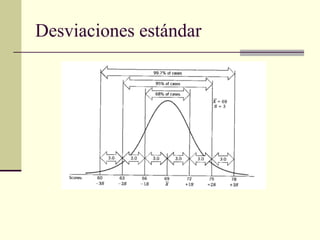
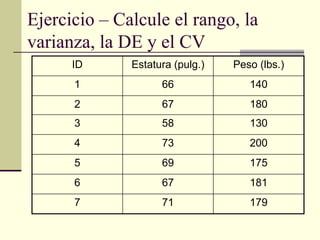
Este documento presenta diferentes medidas de variabilidad que pueden usarse para describir la dispersión de datos, incluyendo el rango, la varianza, la desviación estándar y el coeficiente de variabilidad. Explica cómo calcular cada medida y cómo interpretar los resultados.

1. Estadísticas descriptivas II
Medidas de variabilidad
Prof. Orville M. Disdier

2. Medidas de variabilidad
 Las medidas de tendencia central por si solas
no cuentan toda la historia.
 Son indicadores del grado de dispersión de
los datos.

3. Promedio versus variabilidad
Población Datos Promedio
A 9, 5, 6, 2, 3, 3 4.7
B 10, 7, 7, 1, 2, 1 4.7
Población Datos Variabilidad
A 9, 5, 6, 2, 3, 3 6.7
B 10, 7, 7, 1, 2, 1 14.7

4. Medidas de variabilidad
 Es un número real y nunca es <0.
 Si es 0 todos los datos son idénticos
 Aumenta según los datos se hacen más
diversos

5. Tipos de medidas
 Rango o amplitud
 Varianza
 Desviación estándar
 Coeficiente de variabilidad

6. Rango o amplitud
 Es la diferencia entre el valor más alto y el
valor más bajo en una distribución.
 Mide la “distancia” que existe entre un punto
y otro.
 Se calcula restando el valor máximo del valor
mínimo.
Rango = valor máximo – valor mínimo

7. TABLA 2
MATRICULA DE ESTUDIANTES
Escuela: Aguayo del Norte
GRADO Matricula
1 30
2 32
3 35
4 29
5 28
6 29
7 35
8 24
Rango = valor máximo – valor mínimo
Rango = 35 – 24 = 11
7

8. Desviación del dato
 “Deviation score”
 Indica la distancia entre un dato en particular
y la media o promedio.
 Se denota como:

9. TABLA 2b
MATRICULA DE ESTUDIANTES
Escuela: Aguayo del Norte
GRADO Matricula
X-
1 30 30 – 30.3 = -0.3
2 32 32 – 30.3 = 1.8
3 35 32 – 30.3 = 4.8
4 29 32 – 30.3 = -1.3
5 28 32 – 30.3 = -2.3
6 29 32 – 30.3 = -1.3
7 35 32 – 30.3 = 4.8
8 24 32 – 30.3 = -6.3
La suma de las
desviaciones es 0
9

10. Varianza
 Es el promedio de las desviaciones elevadas
al cuadrado.
 Logra detectar diferencias en las variaciones.
 Es la medida básica de variación.
 Se denota como:

11. TABLA 2c
MATRICULA DE ESTUDIANTES
Escuela: Aguayo del Norte
GRADO Matricula
X-
1 30 30 – 30.3 = -0.3
2 32 32 – 30.3 = 1.8
3 35 35 – 30.3 = 4.8
4 29 29 – 30.3 = -1.3
5 28 28 – 30.3 = -2.3
6 29 29 – 30.3 = -1.3
7 35 35 – 30.3 = 4.8
8 24 24 – 30.3 = -6.3
= SS = (-0.3)2 + (1.8)2 + (4.8)2 + (-1.3)2 + (-2.3)2 + (-1.3)2 + (4.8)2 + (-6.3)2
SS = 95.5
= 95.5 / 8 = 11.9
= 95.5 / 7 = 13.6
11

12. Interpretación de la Varianza
 Se interpreta como “unidades al cuadrado”.
 Es muy útil en procedimientos avanzados
pero fatal como estadística descriptiva.
 Interpretación:
= 95.5 / 7 = 13.6
 La media de la matricula tiene una desviación
promedio de 13.6 estudiantes al cuadrado.

13. Desviación estándar
 Es sencillamente la raíz cuadrada de la
varianza.
 De esta manera se soluciona el problema de
la interpretación.
 Se denota como:

14. Interpretación de la DE
 Se interpreta como “unidades de desviación”.
 Es muy útil para la estadística descriptiva.
 Interpretación:
= = 3.7
 La media de la matricula tiene una desviación
promedio de 3.7 estudiantes.

15. Ejemplo de varianza y desviación
estándar

16. Desviaciones estándar

17. Coeficiente de variabilidad
 Expresa el porcentaje general de variación
de los datos en referencia al promedio.
 Se denota como:
CV = (DE ÷ promedio) x 100
 Ejemplo:
 CV = (3.7 ÷ 30.3) x 100 = 12.2%

18. Ejercicio – Calcule el rango, la
varianza, la DE y el CV
ID Estatura (pulg.) Peso (lbs.)
1 66 140
2 67 180
3 58 130
4 73 200
5 69 175
6 67 181
7 71 179

19. MEDIDAS ESPECIALIZADAS:
Comparación de 2 poblaciones a
través de su variabilidad
19

20. Comparando dos poblaciones