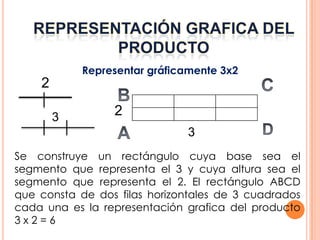
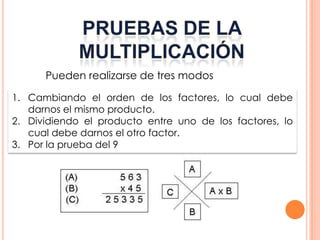
1) La multiplicación es una operación que permite hallar un número llamado producto a partir de un multiplicando y un multiplicador. 2) El producto se indica con el símbolo "x" o punto entre los factores. 3) Las propiedades de la multiplicación incluyen que si el multiplicador es cero el producto es cero, y si el multiplicador es uno el producto es igual al multiplicando.

2. Es una operación de
composición que tiene por
objeto, dados números
llamados multiplicando y
multiplicador, hallar un
numero llamado producto
que sea respecto del
multiplicando lo que el
multiplicador es respecto
de la unidad.

3. El producto de dos números se indica con el
signo X o con punto colocado entre los
factores, que es el nombre que se le da al
multiplicando y multiplicador.
Así, el producto de 6 por 5 se indica 6 x 5 o
6·5

4. 1) Si el multiplicador es cero, el producto es
cero.
2) Si el multiplicador es 1, el producto es igual
al multiplicando.
3) Si el multiplicador es >1, el producto es > el
multiplicando.
4) Si el multiplicador es < 1, el producto es < el
multiplicando.

5. Cuando el multiplicador es
un numero natural, la
multiplicación es una suma
abreviada que consta de
tantos sumandos iguales al
multiplicando como
4x3=
unidades tenga el
4+4+4+4=12
multiplicador

6. Para multiplicar un entero por la unidad seguida
de ceros se añaden al entero tantos ceros
como ceros acompañen a la unidad.
54 x 100 = 5400, por que el valor relativo de
cada cifra se ha hecho 100 veces mayor

7. Se multiplican los números como si no
tuvieran ceros y a la derecha de este
producto se añaden tantos ceros como haya
en el multiplicando y multiplicador.
4300 x 2500 = 107 500 000

8. En el producto hay siempre tantas
cifras como haya en el multiplicando
y multiplicador juntos o una menos.
Así, el 345 x 23 > 345 x 10, y como
producto 345 este ultimo producto 345 x
x 23 ha de 10 = 3450 tiene cuatro
tener cuatro cifras, el producto 345 x 23,
cifras o cinco. que es mayor que el, no
puede tener menos de
7935 cuatro cifras.

9. Representar gráficamente 3x2
2
3 2
3
Se construye un rectángulo cuya base sea el
segmento que representa el 3 y cuya altura sea el
segmento que representa el 2. El rectángulo ABCD
que consta de dos filas horizontales de 3 cuadrados
cada una es la representación grafica del producto
3x2=6

10. Para hallar el producto de mas de dos números como
2x3x4x5
1. Se halla el producto de dos de ellos.
2. Luego se multiplica este producto por el tercero.
3. Luego este segundo producto por el factor
siguiente y así hasta el ultimo factor.
Así, en este caso, tendremos:
2x3=6
6 x 4 = 24
24 x 5 = 120

11. Pueden realizarse de tres modos:
1. Cambiando el orden de los factores, lo cual debe
darnos el mismo producto.
2. Dividiendo el producto entre uno de los factores, lo
cual debe darnos el otro factor.
3. Por la prueba del 9

12. Son 6:
1.- Ley de uniformidad.
2.- Ley disociativa.
3.- Ley conmitativa.
4.- Ley monotonía.
5.- Ley asociativa.
6.- Ley distributiva.

13. Enunciarse de tres modos:
1. El producto de dos números tiene un valor único o
siempre igual.
2. Los productos de números respectivamente
iguales son iguales.
3. Productos de dos igualdades. Multiplicando
miembro a miembro varias igualdades resulta otra
igualdad.
5 sillas x 2 = 10 sillas
a=b 5 días x 2 = 10 días
c=d 5 x 2 = 10
ac = bd

14. El orden de los factores no altera el
producto
2. Que se trate de
1. Que se trate de mas de dos
dos factores factores
Vamos a demostrar
Sea el producto 5 x 4 x 3 x 2
que 6 x 4 = 4 x 6.
Se puede considerar
6x 4 = 6 + 6+ 6+ 6+ 6= 24 descompuesto en dos
4 x 6= 4+ 4+ 4+ 4+ 4 +4= 24 factores: 5 . 4 y 3 . 2

15. Ley asociativa
El producto de varios números no varia
sustituyendo dos o mas factores por su
producto
En general:
2 x 3 x 4 x 5 = 120
(2 x 3) x 4 x 5 = 120 abcd = (ab)cd = a(bcd)
6
(2 x 3) x (4 x 5) = 120
6 20

16. Ley disociativa
El producto de Sea el producto 8 x
varios números 5; puesto que 8 = 4 x
no varia 2, tendremos:
descomponien
do uno o mas 8x5=4x2x5
factores en dos
o mas factores