regresiones

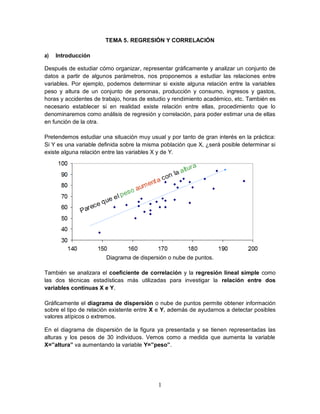
1. 1
TEMA 5. REGRESIÓN Y CORRELACIÓN
a) Introducción
Después de estudiar cómo organizar, representar gráficamente y analizar un conjunto de
datos a partir de algunos parámetros, nos proponemos a estudiar las relaciones entre
variables. Por ejemplo, podemos determinar si existe alguna relación entre la variables
peso y altura de un conjunto de personas, producción y consumo, ingresos y gastos,
horas y accidentes de trabajo, horas de estudio y rendimiento académico, etc. También es
necesario establecer si en realidad existe relación entre ellas, procedimiento que lo
denominaremos como análisis de regresión y correlación, para poder estimar una de ellas
en función de la otra.
Pretendemos estudiar una situación muy usual y por tanto de gran interés en la práctica:
Si Y es una variable definida sobre la misma población que X, ¿será posible determinar si
existe alguna relación entre las variables X y de Y.
Diagrama de dispersión o nube de puntos.
También se analizara el coeficiente de correlación y la regresión lineal simple como
las dos técnicas estadísticas más utilizadas para investigar la relación entre dos
variables continuas X e Y.
Gráficamente el diagrama de dispersión o nube de puntos permite obtener información
sobre el tipo de relación existente entre X e Y, además de ayudarnos a detectar posibles
valores atípicos o extremos.
En el diagrama de dispersión de la figura ya presentada y se tienen representadas las
alturas y los pesos de 30 individuos. Vemos como a medida que aumenta la variable
X=”altura” va aumentando la variable Y=”peso”.

2. 2
Aparentemente, el peso aumenta 10 Kg por cada 10 cm de altura, es decir, el peso
aumenta en una unidad por cada unidad de altura. Asimismo, el diagrama de dispersión
se obtiene representando cada observación (Xi, Yi) como un punto en el plano cartesiano
XY.
Las técnicas de correlación y las de regresión están estrechamente relacionadas, aunque
obedecen a estrategias de análisis un tanto diferentes.
La relación que puede existir entre dos variables, las podemos clasificar de la siguiente
manera:
 Dependencia causal unilateral. Esta relación se da cuando una de las variables
influye en la otra, pero no al contrario.
 Interdependencia. Se presenta cuando la influencia entre las dos variables es
recíproca. Sería un caso de dependencia bilateral.
 Dependencia indirecta. Dos variables pueden mostrar una correlación a través
de una tercera variable que influye en ellas.
 Concordancia. Se presenta en dos variables independientes a las cuales se les
determina la correlación que puede existir.
 Covariación casual. Cuando la correlación que se presenta entre las dos
variables es totalmente casual o accidental.
Por un lado, el coeficiente de correlación determina el grado de asociación lineal entre
X e Y, sin establecer a priori ninguna direccionalidad en la relación entre ambas variables.
Por el contrario, la regresión lineal simple permite cuantificar el cambio en el nivel medio
de la variable Y conforme cambia la variable X, asumiendo implícitamente que X es la
variable explicativa o independiente e Y es la variable respuesta o dependiente.

3. 3
b) Regresión y correlación lineal
Correlación
La finalidad de la correlación es examinar la dirección y la fuerza de la asociación entre
dos variables cuantitativas. Así conoceremos la intensidad de la relación entre ellas y si, al
aumentar el valor de una variable, aumenta o disminuye el valor de la otra variable.
Para valorar la asociación entre dos variables, la primera aproximación suele hacerse
mediante un diagrama de dispersión.
En el diagrama de dispersión de la figura que antecede parece existir una relación lineal
entre el peso y la estatura. Además, si nos fijamos parece que existe un dato atípico que
se aleja de la nube de puntos.
Con la nube de puntos podemos apreciar si existe o no una tendencia entre las dos
variables, pero si queremos cuantificar esta asociación debemos calcular un coeficiente
de correlación.
El coeficiente de correlación de Pearson evalúa específicamente la adecuación a la recta
lineal que defina la relación entre dos variables cuantitativas. El coeficiente no paramétrico
de Spearman mide cualquier tipo de asociación, no necesariamente lineal.
El análisis de correlación busca establecer esencialmente tres cosas:
1) Presencia o ausencia de correlación. Dadas dos o más variables, si existe o no
correlación entre ellas.
2) Tipo de correlación. En caso de existir correlación, si esta correlación es directa o
inversa. En la correlación directa, ambas variables aumentan (o disminuyen)
concomitantemente, y en la correlación inversa ambas variables varían inversamente, o
también puede decirse "en relación inversamente proporcional", lo que significa que
cuando una aumenta la otra disminuye, o viceversa (2). En el siguiente esquema se
muestran algunos ejemplos de correlación directa e inversa.

4. 4
Tipos de correlación
Tipo Definición Ejemplos
Correlación
directa o
positiva
Ambas variables
aumentan (o disminuyen)
en forma concomitante.
Cociente intelectual/calificación: A mayor CI, mayor
calificación obtenida en el examen.
Tiempo/retención: A mayor tiempo para memorizar,
mayor cantidad de palabras retenidas.
Test laboral/rendimiento futuro: A mayor puntaje en
un test de aptitud técnica, mayor rendimiento en
dicha área dentro de x años (esto es también un
modo de estimar la validez predictiva de un test).
Correlación
inversa o
negativa
Una variable aumenta y la
otra disminuye (o
viceversa) en forma
concomitante.
Edad/memoria: Al aumentar la edad, disminuye la
memoria.
Numero de ensayos/cantidad de errores: Al
aumentar el número de ensayos, disminuye la
cantidad de errores.
Cansancio/atención: Al aumentar el cansancio
disminuye la atención.
3) Grado de correlación. El grado o “intensidad‟ de la correlación, es decir, “cuánta‟
correlación tienen en términos numéricos.
Para hacer todas estas averiguaciones, se puede recurrir a tres procedimientos.
a) El método tabular. Una correlación podría constatarse a simple visualización de
tablas de correlación como las indicadas anteriormente, pero habitualmente las
cosas no son tan fáciles, sobre todo porque hay bastante mayor cantidad de datos,
y porque estos casi nunca registran los mismos incrementos para ambas
variables. Por lo tanto, debe abandonarse la simple visualización de las tablas y
utilizar procedimientos más confiables, como los gráficos (diagramas de dispersión
o dispersiogramas) y los analíticos (por ejemplo el coeficiente de Pearson).
b) El método gráfico. Consiste en trazar un diagrama de dispersión.
Diferentes diagramas de dispersión.

5. 5
c) El método analítico. Consiste en aplicar una fórmula que permita conocer no sólo
el tipo de correlación (directa o inversa) sino también una medida cuantitativa
precisa del grado de correlación. La fórmula del coeficiente de Pearson es un
ejemplo típico para medir correlación entre variables cuantitativas.
Si se desea medir o cuantificar el grado de asociación entre dos variables cuantitativas
se debe calcular un coeficiente de correlación (r).
Coeficiente de correlación lineal
El coeficiente de correlación lineal de Pearson (r) mide la fuerza de asociación lineal
con que dos variables aleatorias están ligadas (linealmente). Esta fuerza es medida por el
coeficiente de correlación lineal poblacional (ρ). El coeficiente de correlación lineal
poblacional es adimensional (no depende de las unidades de medida) y puede tomar
valores en el intervalo [−1 a +1]. Para interpretar el coeficiente de correlación lineal
debemos interpretar por separado su magnitud y su signo:
Su signo indica el sentido de la asociación:
 ρ > 0 ⇒ Asociación positiva. Al aumentar los valores de una de las variables
aumentan los valores de la otra.
 ρ < 0 ⇒ Asociación negativa. Al aumentar los valores de una de las variables
disminuyen los valores de la otra.
Su magnitud indica la fuerza de la asociación:
 ρ cercano a 0 ⇒ Independencia lineal o falta de asociación lineal.
 ρ cercano a 1 o -1 ⇒ Fuerte asociación lineal.
El coeficiente de correlación de la muestra, simbolizada por r, es un estadístico que mide el
grado de asociación entre dos variables.

6. 6
Matemáticamente se define como:
∑
√ ∑ ̅
̅̅̅ ∑
∑
√∑ ∑
∑
∑ ∑
√ ∑
∑
∑
∑
El coeficiente de Pearson o correlación es un número comprendido entre -1 y +1, y que
posee un determinado signo (positivo o negativo). El valor numérico indica „cuanta‟
correlación hay, mientras que el signo indica que “tipo‟ de correlación es (directa si el
signo es positivo, inversa si es negativo). En el siguiente esquema se muestran algunos
posibles valores de “r”.
Ejemplo:
Se tiene datos de la edad en semanas y peso promedio en kilogramos de un conjunto de
cerdos, en una granja, determinar el coeficiente de correlación.
X
Edad
(Semanas)
Y
Peso Promedio
(Kilogramos)
X2
Y2
XY Ye
8
10
12
14
16
18
20
22
17.97
24.56
31.15
35.07
49.45
59.72
68.80
76.22
64
100
144
196
256
324
400
484
322.9209
603.1936
970.3225
1229.9049
2445.3025
3566.3784
4733.4400
5809.4884
143.76
245.60
373.80
490.98
791.20
1074.96
1376.00
1676.84
16.76
24.85
32.95
41.04
49.14
57.23
65.32
73.42

7. 7
24
26
28
86.77
89.03
90.78
576
676
784
7522.0329
7926.3409
8241.0084
2082.48
2314.78
2541.84
81.51
89.60
97.70
198 629.52 4004 43377.4334 13112.24 629.52
√
Diagrama de dispersión de los datos de edad y peso.
En efecto, su interpretación depende de varios factores, como por ejemplo: a) la
naturaleza de las variables que se correlacionan; b) la significación del coeficiente; c) la
variabilidad del grupo; d) los coeficientes de confiabilidad de los tests; e) el propósito para
el cual se calcula r.
Matriz de correlaciones, en muchas investigaciones se estudian muchas variables, y se
intenta cuantificar mediante el coeficiente „r‟ sus relaciones dos a dos, es decir, las
relaciones de cada variable con cada una de las demás (Botella, 1993:202). A los efectos
de comparar estos diferentes valores de „r‟ se traza una matriz de correlación, que puede
tener la siguiente forma:
Variable X Variable Y Variable W Variable Z
Variable X r= -0.17 r = -0.11 r = -0.30
Variable Y r = +0.46 r = +0.17
Variable W r = +0.10
Variable Z

8. 8
La matriz permite visualizar inmediatamente, entre otras cosas, cuáles son los
coeficientes de correlación más altos (en este caso, entre Y y W).
Coeficiente de determinación
El conocimiento del coeficiente de correlación, como se ha expresado, sirve para indicar el
grado de asociación de dos variables, pero no ofrece información alguna de la influencia
que tiene una variable sobre otra. Para este propósito, r2
el coeficiente de determinación es
más fácil de calcular a partir de un análisis de regresión.
Por tanto, el coeficiente de determinación r2
es la relación que existe entre la suma de
cuadrados de la regresión y la suma de cuadrados de Y.
El coeficiente de determinación puede interpretarse como un indicador de la proporción en
la variabilidad total de Y que se debe al efecto de la variable X. multiplicando el valor de r2
por cien, la proporción se convierte en un porcentaje.
Para el ejemplo anterior tenemos:
100* r2
= 100*(0.99)2
= 98%
Nos indica que el 98% de la variación en el peso de los cerdos se debe a la relación lineal
que existe entre el peso y la edad de los animales, y que la diferencia se debe a factores
propios del azar, comúnmente involucrados como “error experimental”.
Pruebas de significación
Una de las hipótesis más utilizadas en correlación es la que supone que el coeficiente de
correlación es igual a cero; esto es Ho: ρ = 0.
Uso de las distribuciones F y t
Se sabe que F es igual a:
=
Al usar F puede expresarse en términos de r y n como:

9. 9
Pudiéndose por consiguiente, usar F con 1 y n-2 grados de libertad para probar esta
hipótesis. Pero cuando F tiene 1 y ν grados de libertad, F = t2
; por lo tanto
√
√
Sigue la distribución t de “Student” con n-2 grados de libertad, pudiéndose usar como una
prueba análoga a la de F.
Por la relación existente entre y F, la prueba de significación para r es equivalente a la
prueba para b. si una es significativa, la otra debe serlo también y viceversa. En la práctica,
la prueba de significación de r no tiene mucha importancia, basta solamente con realizarla
para b, y es más bien de mayor utilidad 100r2
que es un buen indicador de la bondad de
ajuste.
Análisis de Regresión
La regresión está dirigida a describir como es la relación entre dos variables X e Y, de
tal manera que incluso se pueden hacer predicciones sobre los valores de la variable Y,
a partir de los de X. Cuando la asociación entre ambas variables es fuerte la regresión
nos ofrece un modelo estadístico que puede alcanzar finalidades predictivas.
La regresión supone que hay una variable fija, controlada por el investigador (es la
variable independiente o predictora), y otra que no está controlada (variable respuesta o
dependiente). La correlación supone que ninguna es fija: las dos variables están fuera del
control de investigador.
La regresión es su forma más sencilla se llama regresión lineal simple. Se trata de una
técnica estadística que analiza la relación entre dos variables cuantitativas, tratando de
verificar si dicha relación es lineal.
Si tenemos dos variables hablamos de regresión simple, si hay más de dos variables
regresión múltiple.
Su objetivo es explicar el comportamiento de una variable Y, que denominaremos
variable explicada (o dependiente o endógena), a partir de otra variable X, que
llamaremos variable explicativa (o independiente o exógena).

10. 10
Mediante las técnicas de regresión inventamos una variable Ŷ como función de otra
variable X (o viceversa).
El criterio para construir esta función es que la diferencia entre Y e Ŷ, denominada error
o residuo, sea pequeña.
Ŷ = f(x), Y- Ŷ = error
Los residuos o errores ei son las diferencias entre los valores observados (verdadero
valor de Y) y los valores pronosticados por el modelo: ei =Y-Ŷ. Recogen la parte de la
variable Y que no es explicada por el modelo de regresión.
A partir de la definición de residuo, podemos escribir Y = f(X) + error.
El término que hemos denominado error debe ser tan pequeño como sea posible. El
objetivo será buscar la función (modelo de regresión) Ŷ = f(X) que lo minimice.
Una vez que se cuenta con un determinado conjunto de pares de valores obtenidos de la
realidad, puede determinarse la ecuación de la recta que los representan por dos
métodos: el método de los cuadrados mínimos, y el método de las desviaciones.
Antes de examinarlos, debe tenerse presente que la forma general de una ecuación de
una recta es:
y = a + bx
Determinar la ecuación de la recta significa asignarle un valor al parámetro “a‟ y otro
valor al parámetro “b‟. Los métodos indicados tienen como fin determinar el valor de
ambos parámetros.
En la ecuación anterior se encuentra cuatro componentes:
 Ŷ es la variable que se va a estimar en función de otra variable (X) supuestamente
conocida. Se le denomina también como variable dependiente, explicada o
predictando.
 X es la variable cuyo valor que supuestamente se conoce. Se le denomina variable
independiente, predictor o explicativa.
 b=B=β es la pendiente, la que nos determina el ángulo de inclinación de la recta.
Denominada también coeficiente angular, que nos permite cuantificar la cantidad
que aumenta o decrece Ŷ, por cada valor que toma la variable independiente (X) o
explicativa.
El coeficiente angular puede ser representado de las siguientes formas:

11. 11
Si b es un valor mayor que 0, es decir, positivo, nos indicara que la recta es ascendente;
si b es menor que 0, la recta será descendente, y si b es igual a 0 será una paralela al eje
horizontal.
Por otra parte, la regresión nos permite establecer los siguientes aspectos:
1. Permite cuantificar la magnitud del cambio de la variable dependiente por cada
unidad de cambio en la variable independiente a través del coeficiente de
regresión.
2. Estimar el valor de variable dependiente en base a los valores establecidos de la
variable independiente a través de la ecuación de regresión.
c) La recta de regresión de mínimos cuadrados
El método de los mínimos cuadrados consiste en buscar los valores de los parámetros
a y b de manera que la suma de los cuadrados de los residuos sea mínima. Esta recta es
la recta de regresión por mínimos cuadrados.
La regresión lineal consiste en encontrar (aproximar) los valores de una variable a partir
de los de otra, usando una relación funcional de tipo lineal, es decir, buscamos valores
para a (ordenada en el origen) y b (pendiente de la recta lineal) tales que se pueda
escribir Ŷ = a+bX, con el menor error posible entre Ŷ e Y.
Para cada valor observado de la variable independiente Xi podemos considerar dos
valores de la variable dependiente, el observado Yi y el estimado a partir de la ecuación
de la recta, Ŷi = a+bXi.
Para cada observación podemos definir el error o residuo como la distancia vertical
entre el punto (xi, yi) y la recta, es decir: yi – (a + bxi).
Las cantidades a y b que minimizan dicho error son los llamados coeficientes de
regresión:

12. 12
Las fórmulas para el cálculo de a y b son las siguientes:
∑
∑ ∑
∑
∑
∑ ∑ ∑
∑ ∑
El coeficiente de regresión (b), indica el monto de cambio en la variable dependiente (Y),
por cada unidad de cambio en la variable independiente X, representa la pendiente de la
recta.
La cantidad b se denomina “coeficiente de regresión de Y sobre X”.
Intercepto (a), indica el punto donde la recta de regresión cruza al eje Y.
∑ ∑
a = ȳ - bX
Interpretación de la ordenada en el origen a:
Este parámetro representa la estimación del valor de Y cuando X es igual a cero.
Interpretación de la pendiente de la recta b:
El coeficiente de regresión es muy importante, porque mide el cambio de la variable Y
por cada unidad de cambio de X. Este parámetro nos informa de cómo están
relacionadas las dos variables en el sentido de que nos indica en qué cantidad (y si es
positiva o negativa) varían los valores de Y cuando varían los valores de la X en una
unidad. De hecho el coeficiente de regresión b y el coeficiente de correlación r siempre
tendrán el mismo signo.
 Si b > 0, cada aumento de X se corresponde con un aumento de Y;
 Si b < 0, Y decrece a medida que aumenta X.

13. 13
El método de los mínimos cuadrados consiste en buscar los valores de los parámetros
a y b de manera que la suma de los cuadrados de los residuos sea mínima. Esta recta es
la recta de regresión por mínimos cuadrados.
Ejemplo:
En un estudio de relación entre la publicidad por radio y las ventas de un producto,
durante 10 semanas se han recopilado los tiempos de duración en minutos de la
publicidad por semana (X), y el número de artículos vendidos (Y), resultando:
Semana 1 2 3 4 5 6 7 8 9 10
Publicidad X 20 30 30 40 50 60 60 60 70 80
Ventas Y 50 73 69 87 108 128 135 132 148 170
a) Trazar el diagrama de dispersión, e indicar la tendencia.
b) Calcular la recta de regresión de mínimos cuadrados con el fin de predecir las
ventas:
c) Estimar la venta si en una semana se hacen 100 minutos de propaganda.
d) Calcular el coeficiente de correlación.
a) Si en la novena semana se incrementara la publicidad en 5 minutos, ¿en cuánto
se estima que incrementen las ventas?.
Solución:
a) Trazamos el diagrama de dispersión y vemos que hay una relación lineal positiva
entre el número de artículos vendidos y el tiempo de publicidad semanal realizada
por radio.
b) Determinamos la recta de regresión de mínimos cuadrados a partir de los
planteados, es decir, a y b.
De los datos propuestos tenemos:

14. 14
n = 10 ƩX = 500 ƩY = 1100 ƩXY = 61800
ƩX2
=28400 ƩY2
= 134660 X = 500/10 = 50 ȳ = 1100/10 = 110
X Y XY X2
Y2
20
30
30
40
50
60
60
60
70
80
50
73
69
87
108
128
135
132
148
170
1000
2190
2070
3480
5400
7680
8100
7920
10360
13600
400
900
900
1600
2500
3600
3600
3600
4900
6400
2500
5329
4761
7569
11664
16384
18225
17424
21904
28900
500 1100 61800 28400 134660
Una forma de calcular b es:
∑ ∑ ∑
∑ ∑
La otra forma de calcular b es:
∑
∑
Además, a = ȳ - bX = 110 – 2(50) = 10
Por tanto, la recta de regresión es: Y = 10 + 2X
También utilizando Y - ȳ = b(X – X), se tiene:
Y – 110 = 2(X – 50) ò Y = 10 + 2X
c) Si X1 = 100, ȳ = 10+2(100) = 210. No se tiene por el momento un criterio para
concluir que este pronóstico es confiable.
d) El coeficiente de correlación es:

15. 15
Es altamente positivo. Es un primer criterio para analizar la validez de la predicción.
e) Si en la novena semana se incrementa el tiempo de propaganda en 5 minutos,
entonces, la venta se incrementa en promedio 5*2 = 10 unidades.
Ejemplo:
Utilizando los datos del ejemplo anterior, calcular el intercepto, el coeficiente de regresión,
la ecuación, los valores de Ye y la línea de regresión.
X
Edad
(Semanas)
Y
Peso Promedio
(Kilogramos)
X2
Y2
XY Ye
8
10
12
14
16
18
20
22
24
26
28
17.97
24.56
31.15
35.07
49.45
59.72
68.80
76.22
86.77
89.03
90.78
64
100
144
196
256
324
400
484
576
676
784
322.9209
603.1936
970.3225
1229.9049
2445.3025
3566.3784
4733.4400
5809.4884
7522.0329
7926.3409
8241.0084
143.76
245.60
373.80
490.98
791.20
1074.96
1376.00
1676.84
2082.48
2314.78
2541.84
16.76
24.85
32.95
41.04
49.14
57.23
65.32
73.42
81.51
89.60
97.70
198 629.52 4004 43377.4334 13112.24 629.52
Aplicando la siguiente formula encontrar b:
∑
∑ ∑
∑
∑
Este valor significa que a partir de la octava semana, el peso del cerdo incrementa en
4.047 kilogramos semanalmente.
Conocido b, el intercepto se calcula con la fórmula:
∑ ∑
Usando los valores de a y b, la ecuación de regresión será la siguiente

16. 16
Ye = - 15.617 + 4.047X
La ecuación de regresión sirve para encontrar los valores de Ye que corresponde a cada
valor de X, obteniéndose la línea de mejor ajuste. Al reemplazar el valor de X en la
ecuación de Ye, se obtienen los valores de Ye, los cuales aparecen en la última columna
de la tabla.
Si tomamos los puntos extremos de X, y se ubican en un sistema de ejes coordinados los
lugares geométricos correspondientes a esos puntos (8, 16.76) y (28, 97.70), y uniendo
estos puntos mediante una recta se tendrá la línea de regresión que corresponde a los
datos del ejemplo.