apuntes unidad 2 y 3.pdf

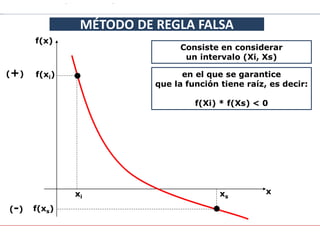
xi xs
f(x)
x
f(xi)
f(xs)
2
MÉTODO DE REGLA FALSA
CURSO DE ANÁLISIS NUMÉRICO. BLOQUE 1
•
•
Consiste en considerar
un intervalo (Xi, Xs)
(+)
(-)
en el que se garantice
que la función tiene raíz, es decir:
f(Xi) * f(Xs) < 0

xi xs
f(x)
x
f(xi)
f(xs)
3
•
•
Se traza una recta que
une los puntos
(Xi , f(Xi)) , (Xs , f(Xs))
(+)
(-)

xi xs
f(x)
x
f(xi)
f(xs)
4
•
•
Se obtiene el punto de
intersección de esta recta
con el eje de las abscisas: (Xr, 0);
se toma Xr como aproximación
de la raíz buscada.
(+)
(-)
f(xr)
xr
(-)

xi xs
f(x)
x
f(xi)
f(xs)
5
•
•
(+)
(-)
f(xr)
xr
)
x
(
f
)
x
(
f
)
x
x
)(
x
(
f
x
x
s
i
s
i
s
s
r
-
-
-
=
Xr se calcula mediante
esta expresión:
(-)

xi xs
f(x)
x
f(xi)
f(xs)
6
•
•
(+)
(-)
f(xr)
xr
Se evalúa f(xr) para determinar en cuál
de los dos intervalos está la raíz:
f(xi)*f(xr) < 0
La raíz está en el intervalo [ xi , xr ]
f(xi)*f(xr) > 0
La raíz está en el intervalo [ xr , xs ]
(-)

xi xs
f(x)
x
f(xi)
f(xs)
7
•
•
(+)
(-)
f(xr)
xr
Se evalúa f(xr) para determinar en cuál
de los dos intervalos está la raíz:
f(xi)*f(xr) < 0
f(xi)*f(xr) > 0
La raíz está en el intervalo [ xr , xs ]
(-)
En este caso

xi xs
f(x)
x
f(xi)
8
•
(+)
f(xs)
xr
El Xr obtenido se convierte
en el nuevo Xi o Xs según el caso
y se repite el cálculo:
(-)
)
x
(
f
)
x
(
f
)
x
x
)(
x
(
f
x
x
s
i
s
i
s
s
r
-
-
-
=

f(x)
x
f(xi)
9
•
(+)
El proceso se repite, hasta que
se supera una tolerancia
previamente fijada
o se alcanza un número de
iteraciones predeterminado

Sea f(x) una función la cual tiene al menos una raíz, donde f'(x) es continua, si contamos con un valor
próximo a alguna raíz podemos seguir acercándonos mediante aproximaciones sacando rectas
tangentes a la función y el punto donde la recta cruza el eje de las x será la nueva aproximación.

MÉTODO DE BISECCIÓN – TEORÍA
Es el método más simple que se puede emplear para resolver ecuaciones.
Sólo requiere que la función sea continua y que hayamos localizado un cambio de signo de la misma en los
extremos de cierto intervalo en el que empezaremos a trabajar.
Consiste en la aplicación reiterada del conocido teorema de Bolzano, una vez asegurada la existencia de al menos
una solución de la ecuación (1) en el intervalo [a,b].
El único inconveniente es la posible existencia de más de una de estas raíces, ya que el teorema de Bolzano no
nos asegura la unicidad de la misma. Pero en todo caso el correspondiente algoritmo siempre conducirá a la
aproximación numérica de una de estas raíces.
Nos podemos ayudar de una representación gráfica previa de la función para seleccionar un intervalo en el que
sólo exista una de estas raíces.
Teorema de Bolzano:
Sea ƒ : [a,b] → R una función continua en [a,b] y tal que ƒ(a) · ƒ(b) < 0.
Entonces existe s  (a,b) tal que ƒ(s) = 0.
Bolzano dice: “cuando una función es continua en un intervalo y tiene distinto signo en los extremos del
mismo, entonces tiene por lo menos una raíz en ese intervalo”.
(Extraído de “Matemática І”, Santillana, capítulo 7, página 159).
Descripción del algoritmo:
 Supongamos que ƒ verifica las hipótesis del teorema de Bolzano en cierto subintervalo [ak,bk] del intervalo
partida [a,b] ≡ [a0,b0]. Entonces, también podemos asegurar la existencia de por lo menos una raíz de la
ecuación, s  (ak,bk).
 Sabemos que para hallar el punto medio de un intervalo [ak,bk], hacemos:
xk = ½ (ak + bk)
En valor absoluto, el error cometido al tomar xk como aproximación de s es inferior a ½ (bk – ak). Lo indicamos
de la siguiente manera: εa = | s – xk | < | ½ (bk – ak) |
Donde εa es el error absoluto; s es la raíz, es decir el valor verdadero; xk es el valor aproximado;
| ½ (bk – ak) | es la cota de error obtenida en el proceso de iteración.
Entonces, ¿qué representa el valor de cada punto medio hallado?
Representa el valor de la posible raíz aproximada de la función.
 Como ƒ es conocida la podemos especializar en xk y ver si en este punto es una raíz exacta de la ecuación,
en cuyo caso ya habríamos finalizado la búsqueda.
En caso contrario, podemos determinar el signo de la función en el centro de este intervalo, de tal forma que
dicho signo será opuesto del que tiene ƒ en uno de los extremos, ya que ƒ (xk) ≠ 0 y ƒ(a) · ƒ(b) < 0.
Así, eligiendo el extremo en el que ƒ tiene signo opuesto que en el centro, tenemos un nuevo intervalo que
denotaremos con [ak+1,bk+1], de tamaño mitad que el anterior, en el cual seguimos teniendo asegurado que ƒ
tiene una raíz. La nueva aproximación será el centro de este nuevo intervalo y el error máximo cometido (cota)
es la mitad de la longitud del mismo, es decir, la cuarta parte de la longitud del intervalo anterior.
En otros términos: εa = |s – xk+1| < |½ (bk+1 – ak+1)| = |(1/2)2
(bk – ak)| = |(1/2)3
(bk–1 – ak–1)| = …
 En general, empezamos para k = 0 con el intervalo de partida, y tras un proceso de inducción, tras k iteraciones,
el valor absoluto del error cometido satisface la desigualdad:
εa = |s – xk | < | ½ (bk – ak)| = | (½)k+1
(b – a)|
Si no se encuentra la solución exacta s = xk , entonces se obtiene una sucesión de intervalos de manera que
si s ε (bk;ak), entonces el error |s – xk| tiende a cero cuando k tiende a infinito y el método resulta convergente,
es decir limk→∞ xk = s en R.

(Extraído de “Cálculo Numérico con Mathemática”, capítulo 2, páginas 38 y 39).
MÉTODO DE BISECCIÓN APLICACIÓN
Dado el polinomio p(x) = x3
– 2x2
– 2x + 4, halla las raíces aproximadas con una precisión de dos cifras
decimales, aplicando el método de bisección.
Comenzamos el análisis teniendo en cuenta los conocimientos previos relativos a funciones. Todos los polinomios
son funciones continuas por lo tanto es posible aplicar el método. El polinomio dado es mónico, porque el coeficiente
principal es 1. Como el “Teorema Fundamental del Algebra” dice que un polinomio de grado n tiene exactamente n
raíces y como este polinomio es de tercer grado tendrá tres raíces. Se grafica el polinomio para poder determinar el
intervalo en el que se encuentran, aproximadamente, las raíces.
A ese intervalo se lo llama de partida: [a,b] = [–3,3].
Según Bolzano sea ƒ: [a,b] → R una función continua en [a,b] / ƒ(a) · ƒ(b) < 0   s  (a,b) / ƒ(s) = 0.
Por lo tanto debemos probar que ƒ(–3) · ƒ(3) < 0 para asegurar que en ese intervalo de partida hay una raíz o un
número impar de raíces.
El intervalo al que pertenece la solución debe ser abierto porque si ésta está en uno de los extremos la expresión
de Bolzano daría igual a cero.
Probamos Bolzano para los extremos del intervalo de partida, especializando el polinomio. En un polinomio P(x),
“x” es la indeterminada. Cuando le asignamos un valor determinado, decimos que el polinomio P(x) está
“especializado” en ese valor. Entonces:
ƒ(–3) =( –3)3
– 2(–3)2
– 2(–3) + 4 = –27 – 18 + 6 + 4 = 10 – 45 = –35
ƒ(3) = 33
– 2 · 32
– 2 · 3 + 4 = 27 – 18 – 6 + 4 = 31 – 24 = 7
Aplicamos Bolzano: ƒ(–3) · ƒ(3) = –35 · 7 < 0 nos asegura que existe una raíz o un número impar de
raíces en el intervalo de partida considerado.
Si al aplicar Bolzano obtenemos una expresión mayor que cero, significa que en ese intervalo no existen
raíces o existe un número par de raíces.
Hallamos el punto medio de dicho intervalo: x0 = ½ (–3 + 3) = 0 x0 = 0
Aquí nos cuestionamos, ¿cómo saber de antemano la cantidad de iteraciones que debemos realizar para
obtener la precisión solicitada?
Tratemos de analizar y dar respuestas a esta pregunta con el objetivo de facilitar la tarea.
Para ello debemos tener en cuenta el intervalo de partida el cual debe ser convenientemente elegido.
La precisión tiene que ver con la cota de error y por lo tanto debemos partir del análisis de ella.
Como el error por redondeo es siempre menor que por truncamiento se considera la cota de error por redondeo,
con la precisión que requiere el problema. Entonces: de la expresión:
εa = |s – xk | < | ½ (bk – ak)| = | (½)k+1
(b – a)|
Al no haber comenzado el proceso, no se puede saber el error cometido al aproximar las raíces de la función, por
lo tanto el valor del error absoluto se considera el de la precisión solicitada en el problema. Al no tener el valor de la
raíz, ni del último punto medio, entonces la expresión queda:
ε < | (½)k+1
(b – a) Hacienda pasaje de término, es:
ε
b−a
<
1
2
k+1
Aplicando logaritmo a ambos miembros de la desigualdad
log
ε
𝑏−𝑎
< log
1
2
𝑘+1
Aplicando propiedades de logaritmo, queda:
log 𝜀 − log(𝑏 − 𝑎) < (𝑘 + 1) log
1
2
Haciendo pasaje de término, es:

log ε − log(𝑏−𝑎)
log
1
2
< 𝑘 + 1 Despejando k, queda:
log ε − log(𝑏−𝑎)
log
1
2
− 1 < 𝑘 Donde k  N porque cuenta la cantidad de iteraciones
Luego de tener el número aproximado de iteraciones que deben realizarse para obtener raíces con la precisión
solicitada, comienza el proceso de iteración:
Observando el gráfico consideramos el subintervalo [–3,0].
Aplicamos Bolzano ƒ(–3) · ƒ(0) = –35 · 4 < 0 nos asegura que existe una raíz o un número impar de raíces.
Hallamos el punto medio del intervalo: x1 = ½ (–3) = –1,5 x1 = –1,5
Especializamos el polinomio en este valor: ƒ(–1,5) = (–1,5)3
– 2(–1,5)2
– 2(–1,5) + 4 = –0,875.
Al no darnos valor cero indica que –1,5 no es raíz del polinomio.
Consideramos el subintervalo [–1,5;0].
Aplicamos Bolzano: ƒ(–1,50) · ƒ(0) = –0,875 · 4 < 0 nos asegura que existe una raíz o un número impar de raíces.
Hallamos el punto medio del intervalo: x2 = ½ (–1,5 + 0) = –0,75 x2 = –0,75
– 2(–0,75)2
– 2(–0,75) + 4 = 3,953.
Tampoco es raíz.
Consideramos el subintervalo [–1,5;–0,75].
Aplicamos Bolzano ƒ(–1,5) · ƒ(–0,75) = –0,875 · 3,983 < 0 nos asegura que existe una raíz o un número impar de
raíces.
Hallamos el punto medio del intervalo: x3 = ½ [(–1,5) + (–0,75)] = –1,125 x3 = –1,125
– 2(–1,125)2
– 2(–1,125) + 4 = 2,295.
Tampoco es raíz y seguimos.
Consideramos el subintervalo [–1,5; –1,125].
Aplicamos Bolzano ƒ(–1,5) · ƒ(1,125) = –0,875 · 2,295 < 0 nos asegura que existe una raíz o un número impar de
raíces.
Hallamos el punto medio del intervalo: x4 = ½[(–1,5) + (–1,125)] = –1,31 x4 = –1,31
– 2(–1,31)2
– 2(–1,31) + 4 = 0,94.
Tampoco es raíz.
Consideramos el subintervalo [–1,5;–1,31].
Aplicamos Bolzano ƒ(–1,5) · ƒ(–1,31) = –0,875 · 0,94 <0 nos asegura que existe una raíz o un número impar de raíces.
Hallamos el punto medio del intervalo: x5 = ½[(–1,5) + (–1,31)] = –1,41 x5 = –1,41
– 2(–1,41)2
– 2(–1,41) + 4 = 0,04
Al obtener este valor podemos considerar que x5 = – 1,41 es la mejor aproximación y por lo tanto
damos por finalizada la búsqueda.
Se han realizado cinco iteraciones para hallar xk = x5 = –1,41.
Consideramos x5 = –1,41 y entonces decimos que  s = −√2  (–1,5; –1,31) / ƒ(–1,41) ≡ 0
Analicemos el error:
εa = |s – xk| < | ½ (bk – ak)|, donde el segundo miembro de esta desigualdad es la cota de error “”
εa = |s – x5| < |1/2 (b5 – a5)| = |1/2k+1
(b – a)|, reemplazando por los valores, tenemos:
εa = |–√2 – (–1,41)| < |½ [–1,31 – (–1,5)]| = |½ 5+1
[3 – (–3)]|
εa = 0,004 < 0,095 = 0,094

Quiere decir que el error absoluto cometido en esta aproximación es 0,004 y la cota de error es 0,095. O sea: a
= 0,004 y  = 0,095
Para la determinación de las otras raíces hacemos el siguiente análisis: s = 2 es una raíz exacta que la obtuvimos
al realizar la tabla de valores para graficar la función.
La tercera raíz s = +√2 la obtuvimos por simetría en el gráfico.
Conclusiones:
1) Las raíces buscadas son dos: ±√𝟐
2) El método nos permite obtener aproximaciones de números irracionales, de los cuales podemos, en
algunos casos, conocer su expresión, pero no su valor numérico.

514 CAPÍTULO 7 Técnicas de integración
(b) Con base en el patrón de sus respuestas del inciso (a), infiera el valor de la integral
y
1
sx 1 adsx 1 bd
dx
si a ? b. ¿Qué pasa si a 5 b?
(c) Verifique su suposición pidiendo a su sac que evalúe la integral del inciso (b). Luego
demuéstrela utilizando fracciones parciales.
2. (a) Utilice un sistema algebraico computacional para evaluar las integrales siguientes.
(i) y sen x cos 2x dx (ii) y sen 3x cos 7x dx (iii) y sen 8x cos 3x dx
(b) Con base en el patrón de sus respuestas del inciso (a), infiera el valor de la integral
y sen ax cos bx dx
(c) Verifique su suposición con un sac. Después demuéstrela utilizando las técnicas de la
sección 7.2. ¿Para qué valores de a y b es esta válida?
(i) y ln x dx (ii) y x ln x dx (iii) y x2
ln x dx
(iv) y x3
ln x dx (v) y x7
ln x dx
(b) Con base en el patrón de sus respuestas del inciso (a), infiera el valor de
y xn
ln x dx
(c) Utilice integración por partes para demostrar la suposición que hizo en el inciso (b). ¿Para
qué valores de n es esto válido?
(i) y xex
dx (ii) y x2
ex
dx (iii) y x3
ex
dx
(iv) y x4
ex
dx (v) y x5
ex
dx
(b) Con base en el patrón de sus respuestas del inciso (a), infiera el valor de y x6
ex
dx. Des-
pués, utilice su sac para verificar su suposición.
(c) Basado en los patrones de los incisos (a) y (b), haga una conjetura sobre el valor de la
integral
y xn
ex
dx
cuando n es un entero positivo.
(d) Utilice inducción matemática para demostrar la suposición que hizo en el inciso (c).
Hay dos situaciones en las cuales es imposible encontrar el valor exacto de una integral
definida.
La primera de ellas surge del hecho de que, al evaluar y
b
a
f(x) dx utilizando el teorema
fundamental del cálculo, se necesita conocer una antiderivada de f. Sin embargo, algunas
veces es difícil, o aun imposible, encontrar una antiderivada (véase la sección 7.5).
7.7 Integración aproximada
Stewart_ch07_504-523.indd 514 09/06/17 11:56 a.m.
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
https://t.me/universitarios_info https://www.jamarana.com https://t.me/universitarios

SECCIÓN 7.7 Integración aproximada 515
Por ejemplo, es imposible evaluar exactamente las integrales siguientes:
y
1
0
ex 2
dx y
1
21
s1 1 x3
dx
La segunda situación surge cuando la función es producto de un experimento cien-
tífico, obtenida a través de lecturas en un instrumento o de una recolección de datos.
Podría no haber fórmula para la función (véase el ejemplo 5).
En ambos casos se necesita encontrar valores aproximados de la integral definida.
Ya se conoce un método. Recuerde que la integral definida se define como el límite
de una suma de Riemann, por lo que se podría utilizar cualquier suma de Riemann
como una aproximación a la integral: si divide [a, b] en n subintervalos de igual longitud
∆x 5 (b 2 a)n, entonces tiene
y
b
a
fsxd dx o
n
i−1
fsxi
*d Dx
donde xi
* es cualquier punto en el i-ésimo subintervalo [xi21
, xi
]. Si se elige xi
* en el punto
final izquierdo del intervalo, entonces xi
* 5 xi21
y tiene
y
b
a
fsxd dx Ln − o
n
i−1
fsxi21d Dx
Si f(x) 0, entonces la integral representa un área y (1) representa una aproximación
a esta área mediante los rectángulos que se muestran en la figura 1(a). Si elige xi
* en el
punto final del intervalo, entonces xi
* 5 xi
y tiene
y
b
a
fsxd dx Rn − o
n
i−1
fsxi d Dx
[Véase la figura 1(b).] Las aproximaciones Ln
y Rn
definidas por las ecuaciones 1 y 2 se
llaman aproximación por el punto final izquierdo y aproximación por el punto final
derecho, respectivamente.
En la sección 5.2 también se considera el caso donde se elige xi
* como el punto medio xi
del subintervalo [xi21
, xi
]. La figura 1(c) muestra la aproximación por el punto medio Mn
,
que parece ser mejor que Ln
o Rn
.
Regla del punto medio
y
b
a
fsxd dx Mn − Dx f fsx1d 1 fsx2 d 1 1 fsxn dg
donde Dx −
b 2 a
n
y xi − 1
2 sxi21 1 xi d − punto medio de fxi21, xi g
Otra aproximación, llamada regla del trapecio, resulta de promediar las aproximacio-
nes de las ecuaciones 1 y 2:
y
b
a
fsxd dx
1
2
Fo
n
i−1
fsxi21 d Dx 1 o
n
i−1
fsxi d DxG−
Dx
2
Fo
n
i−1
sfsxi21 d 1 fsxi ddG
−
Dx
2
fsfsx0 d 1 fsx1dd 1 sfsx1d 1 fsx2 dd 1 1 sfsxn21d 1 fsxn ddg
−
Dx
2
f fsx0 d 1 2 fsx1d 1 2 fsx2 d 1 1 2 fsxn21d 1 fsxn dg
1
⁄ ¤
– – –
–
(a) Aproximación por el punto
final izquierdo
y
x¸ ⁄ ¤ ‹ x¢
x¸ ⁄ ¤ ‹ x¢
‹ x¢
x
0
(b) Aproximación por el punto
final derecho
y
x
0
x
(c) Aproximación por el punto
medio
y
0
FIGURA 1
2
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

Regla trapezoidal
y
b
a
fsxd dx Tn −
Dx
2
f fsx0 d 1 2 fsx1d 1 2 fsx2 d 1 1 2 fsxn21d 1 fsxn dg
donde ∆x 5 (b 2 a)n y xi
5 a 1 i ∆x.
La razón para el nombre de la regla del trapecio puede verse de la figura 2, que ilustra
el caso con f(x) 0 y n 5 4. El área del trapezoide que está encima del i-ésimo subin-
tervalo es
Dx Sfsxi21d 1 fsxi d
2
D−
Dx
2
f fsxi21d 1 fsxi dg
y si se suman las áreas de todos los trapezoides, se obtiene el lado derecho de la regla
del trapecio.
EJEMPLO 1 Utilice (a) la regla del trapecio y (b) la regla del punto medio con n 5 5
para aproximar la integral y
2
1
(1x) dx.
SOLUCIÓN
(a) Con n 5 5, a 5 1 y b 5 2, tiene ∆x 5 (2 2 1)5 5 0.2, por lo que la regla del
trapecio da
y
2
1
1
x
dx T5 −
0.2
2
f fs1d 1 2 fs1.2d 1 2 fs1.4d 1 2 fs1.6d 1 2 fs1.8d 1 fs2dg
− 0.1S1
1
1
2
1.2
1
2
1.4
1
2
1.6
1
2
1.8
1
1
2
D
0.695635
Esta aproximación se muestra en la figura 3.
(b) Los puntos medios de los cinco subintervalos son 1.1, 1.3, 1.5, 1.7 y 1.9, por lo que
la regla del punto medio da
y
2
1
1
x
dx Dx f fs1.1d 1 fs1.3d 1 fs1.5d 1 fs1.7d 1 fs1.9dg
−
1
5
S 1
1.1
1
1
1.3
1
1
1.5
1
1
1.7
1
1
1.9
D
0.691908
Esta aproximación se muestra en la figura 4. n
En el ejemplo 1 elija deliberadamente una integral cuyo valor puede calcularse
explícitamente, así puede ver qué tan precisas son las reglas del trapecio y del punto
medio. Por el teorema fundamental del cálculo,
y
2
1
1
x
dx − ln xg1
2
− ln 2 − 0.693147 . . .
El error al usar una aproximación se define como la cantidad que debe sumarse a la
aproximación para que sea exacta. De los valores en el ejemplo 1, vea que los errores en
0
y
x
x¸ ⁄ ¤ ‹ x¢
1 2
1 2
1
x
y=
1
x
y=
FIGURA 2
Aproximación trapezoidal
FIGURA 3
FIGURA 4
y
b
a
f sxd dx − aproximación 1 error
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

las aproximaciones por las reglas del trapecio y del punto medio para n 5 5 son
ET 20.002488 y EM 0.001239
En general, se tiene
ET − y
b
a
fsxd dx 2 Tn y EM − y
b
a
fsxd dx 2 Mn
Las tablas siguientes muestran el resultado de cálculos similares a los del ejemplo 1,
pero para n 5 5, 10 y 20 y para las aproximaciones por el punto final izquierdo y el dere-
cho, así como las reglas del trapecio y del punto medio.
n Ln Rn Tn Mn
5 0.745635 0.645635 0.695635 0.691908
10 0.718771 0.668771 0.693771 0.692835
20 0.705803 0.680803 0.693303 0.693069
n EL ER ET EM
5 20.052488 0.047512 20.002488 0.001239
10 20.025624 0.024376 20.000624 0.000312
20 20.012656 0.012344 20.000156 0.000078
De estas tablas pueden hacerse varias observaciones:
1. En todos los métodos se obtuvieron aproximaciones más exactas cuando se incre-
menta el valor de n. (Pero valores muy grandes de n requieren de tantas operaciones
aritméticas que se debe considerar del error de redondeo acumulado).
2. Los errores en las aproximaciones del punto final izquierdo y el derecho son de
signo opuesto y al parecer disminuyen por un factor de aproximadamente 2 cuando
se duplica el valor de n.
3. Las reglas del trapecio y del punto medio son mucho más exactas que las
aproximaciones de punto final.
4. Los errores en las reglas del trapecio y del punto medio son de signo opuesto y al
parecer disminuyen por un factor de alrededor de 4 cuando se duplica el valor de n.
5. El tamaño del error en la regla del punto medio es casi la mitad del tamaño del error
en la regla del trapecio.
La figura 5 muestra por qué usualmente se puede esperar que la regla del punto
medio sea más exacta que la del trapecio. El área de un rectángulo representativo en
la regla del punto medio es la misma que la del trapecio ABCD cuyo lado superior es
tangente a la gráfica de P. El área de este trapezoide es más próxima al área bajo la
gráfica de lo que es el área del trapezoide AQRD empleado en la regla del trapecio. [El
error del punto medio (sombreado por encima de la curva) es más pequeño que el error
trapezoidal (sombreado por debajo de la curva).]
Estas observaciones se corroboran en las estimaciones de error siguientes y que se
demuestran en textos de análisis numérico. Note que la observación 4 corresponde a n2
en cada denominador porque (2n)2
5 4n2
. El hecho de que las estimaciones dependan
del tamaño de la segunda derivada no es de sorprender si se considera la figura 5, porque
f0(x) mide qué tanto se curva la gráfica. [Recuerde que f0(x) mide qué tan rápido cambia
la pendiente de y 5 f(x).]
TEC Module 5.27.7 le permite com-
parar métodos de aproximación.
Aproximaciones a y
2
1
1
x
dx
Errores correspondientes
Estas observaciones son verdaderas en
la mayoría de los casos.
C
P
D
A
B
R
Q
C
P
D
A
B
xi-1 xi
i-1 x
–i
FIGURA 5
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

3 Límites de error Suponga que ) f0(x) ) K para a x b. Si ET
y EM
son los
errores en las reglas del trapecio y del punto medio, respectivamente, entonces
|ET |
Ksb 2 ad3
12n2
y |EM |
Ksb 2 ad3
24n2
Aplique esta estimación del error para la aproximación por la regla del trapecio del
ejemplo 1. Si f(x) 5 1x, entonces f9(x) 5 21x2
y f0(x) 5 2x3
. Como 1 x 2, tiene
1x 1, por lo que
| f 0sxd| − Z 2
x3 Z
2
13
− 2
Por tanto, tomando K 5 2, a 5 1, b 5 2 y n 5 5 en la estimación de error (3), vea que
|ET |
2s2 2 1d3
12s5d2
−
1
150
0.006667
Comparando esta estimación de error de 0.006667 con el error real de casi 0.002488, vea
que es posible que el error real sea sustancialmente menor que el límite superior para el
error dado por (3).
EJEMPLO 2 ¿Qué tan grande debería tomarse n para garantizar que las reglas del
trapecio y del punto medio para y
2
1
(1x) dx, tengan una exactitud dentro de 0.0001?
SOLUCIÓN En el cálculo precedente, se vio que u f0(x) 2 para 1 x 2, así
que es posible tomar K 5 2, a 5 1 y b 5 2 en (3). La exactitud dentro de 0.0001
significa que el tamaño del error debería ser menor que 0.0001. Por tanto, elija n de
manera que
2s1d3
12n2
, 0.0001
Resolviendo la desigualdad para n, se obtiene
n2
.
2
12s0.0001d
o n .
1
s0.0006
40.8
Así, n 5 41 asegurará la exactitud deseada.
Para la misma exactitud con la regla del punto medio, elija n tal que
2s1d3
24n2
, 0.0001 por lo que n .
1
s0.0012
29 n
K puede ser cualquier número más
grande que todos los valores de ) f0(x) ),
pero valores más pequeños que K dan
mejores límites de error.
Es muy posible que un valor menor
para n sea suficiente, pero 41 es el
valor más pequeño para el cual la
fórmula del límite del error puede
garantizar exactitud dentro de
0.0001.
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

EJEMPLO 3
(a) Utilice la regla del punto medio con n 5 10 para aproximar la integral y1
0 ex 2
dx.
(b) Dé un límite superior para el error involucrado en esta aproximación.
SOLUCIÓN
(a) Dado que a 5 0, b 5 1 y n 5 10, la regla del punto medio da
y
1
0
ex 2
dx Dx f fs0.05d 1 fs0.15d 1 1 fs0.85d 1 fs0.95dg
− 0.1fe0.0025
1 e0.0225
1 e0.0625
1 e0.1225
1 e0.2025
1 e0.3025
1 e0.4225
1 e0.5625
1 e0.7225
1 e0.9025
g
1.460393
La figura 6 ilustra esta aproximación.
(b) Ya que fsxd − ex 2
, se tiene f9sxd − 2xex 2
y f 0sxd − s2 1 4x2
dex 2
. También, puesto
que 0 x 1, tiene x2
1 y así
0 f 0sxd − s2 1 4x2
dex 2
6e
Tomando K 5 6e, a 5 0, b 5 1 y n 5 10 en el error estimado (3), verá que un límite
superior para el error es
6es1d3
24s10d2
−
e
400
0.007 n
La regla de Simpson
Otra regla para la integración aproximada resulta del uso de parábolas en lugar de seg-
mentos de recta para aproximar la curva. Como antes, divida [a, b] en n subintervalos
de igual longitud h 5 ∆x 5 (b 2 a)n, pero esta vez suponga que n es un número par.
Entonces aproxime la curva y 5 f(x) 0 sobre cada par consecutivo de intervalos,
por una parábola como se muestra en la figura 7. Si yi
5 f(xi
), entonces Pi
(xi
, yi
) es el
punto en la curva que está arriba de xi
. Una parábola representativa pasa por tres puntos
consecutivos Pi
, Pi11
y Pi12
.
0
y
x
a=x¸ ⁄ x™ x¢
x£ xß=b
x∞
P¸ P¡
P™
P¢
P£
Pß
P∞
0
y
x
h
_h
P¸(_h, y¸) P¡(0, ›)
P™(h, fi)
Para simplificar sus cálculos, primero considere el caso donde x0
5 2h, x1
5 0
y x2
5 h (véase la figura 8). Sabe que la ecuación de la parábola que pasa por P0
, P1
y
FIGURA 6
0
y
x
1
y=ex2
El error estimado da el límite supe-
rior para el error. Son escenarios
teóricos del peor de los casos. El
error real en este caso resulta ser de
cerca de 0.0023.
FIGURA 7 FIGURA 8
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

P2
es de la forma y 5 Ax2
1 Bx 1 C y, por tanto, el área bajo la parábola desde x 5 2h
hasta x 5 h es
y
h
2h
sAx2
1 Bx 1 Cd dx − 2 y
h
0
sAx2
1 Cd dx − 2FA
x3
3
1 CxG0
h
− 2SA
h3
3
1 ChD−
h
3
s2Ah2
1 6Cd
Pero, dado que la parábola pasa por P0
(2h, y0
), P1
(0, y1
) y P2
(h, y2
), tiene
y0 − As2hd2
1 Bs2hd 1 C − Ah2
2 Bh 1 C
y1 − C
y2 − Ah2
1 Bh 1 C
y por tanto y0 1 4y1 1 y2 − 2Ah2
1 6C
Así, puede reescribir el área bajo la parábola como
h
3
sy0 1 4y1 1 y2 d
Ahora, si se desplaza esta parábola horizontalmente, el área bajo esta no cambia. Esto
significa que el área bajo la parábola que pasa por P0
, P1
y P2
desde x 5 x0
hasta x 5 x2
en la figura 7 es aún
h
3
sy0 1 4y1 1 y2 d
De manera similar, el área bajo la parábola que pasa por P2
, P3
y P4
de x 5 x2
a x 5 x4
es
h
3
sy2 1 4y3 1 y4 d
Si calcula de esta manera las áreas bajo todas las parábolas y suma los resultados,
obtiene
y
b
a
fsxd dx
h
3
sy0 1 4y1 1 y2 d 1
h
3
sy2 1 4y3 1 y4 d 1 1
h
3
syn22 1 4yn21 1 yn d
−
h
3
sy0 1 4y1 1 2y2 1 4y3 1 2y4 1 1 2yn22 1 4yn21 1 yn d
Aunque ha deducido esta aproximación para el caso en el que f(x) 0, es una
aproximación razonable para cualquier función continua f y se le conoce como regla
de Simpson en honor del matemático inglés Thomas Simpson (1710-1761). Observe el
patrón de coeficientes: 1, 4, 2, 4, 2, 4, 2, . . . , 4, 2, 4, 1.
Regla de Simpson
y
b
a
fsxd dx Sn −
Dx
3
f fsx0 d 1 4 fsx1d 1 2 fsx2 d 1 4 fsx3 d 1
1 2 fsxn22 d 1 4 fsxn21d 1 fsxn dg
donde n es par y ∆x 5 (b 2 a)n
Aquí emplee el teorema 5.5.7.
Observe que Ax2
1 C es par y Bx
es impar.
Simpson
Thomas Simpson fue un autodidacta
en matemáticas que llegó a ser
uno de los mejores matemáticos
ingleses del siglo XVIII. Lo que se
conoce como regla de Simpson, ya
era del dominio de Cavalieri y Gregory
en el siglo XVII, pero Simpson la
popularizó en su libro Mathematical
Dissertations (1743).
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

EJEMPLO 4 Utilice la regla de Simpson con n 5 10 para aproximar y
2
1
(1x) dx.
SOLUCIÓN Poniendo f(x)5 1x, n 5 10 y ∆x 5 0.1 en la regla de Simpson, se obtiene
y
2
1
1
x
dx S10
−
Dx
3
f fs1d 1 4 fs1.1d 1 2 fs1.2d 1 4 fs1.3d 1 ∙ ∙ ∙ 1 2 fs1.8d 1 4 fs1.9d 1 fs2dg
−
0.1
3
S1
1
1
4
1.1
1
2
1.2
1
4
1.3
1
2
1.4
1
4
1.5
1
2
1.6
1
4
1.7
1
2
1.8
1
4
1.9
1
1
2
D
0.693150 n
Observe que, en el ejemplo 4, la regla de Simpson da una mucho mejor aproximación
(S10
0.693150) para los valores verdaderos de la integral (ln 2 0.693147…) que los
de la regla del trapecio (T10
0.693771) o de la regla del punto medio (M10
0.692835).
Resulta (véase el ejercicio 50) que las aproximaciones en la regla de Simpson son prome-
dios ponderados de los de las reglas del trapecio y del punto medio:
S2n − 1
3 Tn 1 2
3 Mn
(Recuerde que usualmente ET
y EM
tienen signos opuestos y u EM
u es casi la mitad del
tamaño de u ET
u).
En muchas aplicaciones de cálculo se necesita evaluar una integral aun cuando no se
conoce ninguna fórmula explícita para y como función de x. Una función puede darse en
forma gráfica o como una tabla de valores de una colección de datos. Si hay evidencia
de que los valores no cambian con rapidez, entonces aún puede utilizarse la regla del
trapecio o la regla de Simpson para encontrar un valor aproximado de y
b
a
y dx, la integral
de y respecto a x.
EJEMPLO 5 La figura 9 muestra el tráfico de datos en la conexión de Estados Unidos
a switch, la red suiza universitaria y de investigación, el 10 de febrero de 1998. D(t)
es el gasto de información, medido en megabits por segundo (Mbs). Utilice la regla
de Simpson para estimar la cantidad total de datos transmitidos en la conexión de la
medianoche hasta el mediodía de ese día.
0
2
4
6
D
8
3 6 9 12 15 18 21 24 t (horas)
SOLUCIÓN Puesto que se desea que las unidades sean congruentes y D(t) se mide
en megabits por segundo, convierta las unidades de t de horas a segundos. Si A(t) es
la cantidad de datos (en megabits), transmitida en el instante t, donde t se mide
en segundos, entonces A9(t) 5 D(t). Así, por el teorema del cambio neto
FIGURA 9
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

(véase la sección 5.4), la cantidad total de datos transmitidos a mediodía (cuando
t 5 12 3 602
5 43 200) es
As43200d − y
43200
0
Dstd dt
Estime los valores de D(t) a intervalos de una hora a partir de la gráfica y compílelos en
la tabla.
t (horas) t (segundos) Dstd t (horas) t (segundos) Dstd
0 0 3.2 7 25200 1.3
1 3600 2.7 8 28800 2.8
2 7200 1.9 9 32400 5.7
3 10800 1.7 10 36000 7.1
4 14400 1.3 11 39600 7.7
5 18000 1.0 12 43200 7.9
6 21600 1.1
Después, utilice la regla de Simpson con n 5 12 y ∆t 5 3600 para estimar la
integral:
y
43,200
0
Astd dt
Dt
3
fDs0d 1 4Ds3600d 1 2Ds7200d 1 1 4Ds39600d 1 Ds43200dg

3600
3
f3.2 1 4s2.7d 1 2s1.9d 1 4s1.7d 1 2s1.3d 1 4s1.0d
1 2s1.1d 1 4s1.3d 1 2s2.8d 1 4s5.7d 1 2s7.1d 1 4s7.7d 1 7.9g
− 143,880
Así, la cantidad total de datos transmitida de la medianoche hasta el mediodía es de
alrededor de 144 000 megabits, o 144 gigabits. n
La tabla en el margen muestra cómo se compara la regla de Simpson con la regla del
punto medio para la integral y
2
1
(1x) dx, cuyo valor es aproximadamente de 0.69314718.
La segunda tabla muestra cómo decrece el error Es
en la regla de Simpson, por un factor
de casi 16 cuando n se duplica. (En los ejercicios 27 y 28 se le pide comprobar esto para
dos integrales adicionales.) Esto es consistente con la aparición de n4
en el denominador
de la estimación de error siguiente para la regla de Simpson. Esto es similar a las esti-
maciones dadas en (3) para las reglas del trapecio y del punto medio, pero se utiliza la
cuarta derivada de f.
4 Límite de error para la regla de Simpson Suponga que | f s4d
sxd| K para
a x b. Si ES
es el error implicado al utilizar la regla de Simpson, entonces
|ES |
Ksb 2 ad5
180n4
EJEMPLO 6 ¿Qué tan grande debe tomar n para garantizar que la aproximación de la
regla de Simpson para y
2
1
(1x) dx sea exacta dentro de 0.0001?
n Mn Sn
4 0.69121989 0.69315453
8 0.69266055 0.69314765
16 0.69302521 0.69314721
n EM ES
4 0.00192729 20.00000735
8 0.00048663 20.00000047
16 0.00012197 20.00000003
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

SOLUCIÓN Si f(x) 5 1x, entonces f(4)
(x) 5 24x5
. Dado que x 1, se tiene 1x 1,
por lo que
| f s4d
sxd| − Z24
x5 Z 24
Por tanto, puede tomar K 5 24 en (4). Por lo que para un error menor de 0.0001,
debería elegir n de manera que
24s1d5
180n4
, 0.0001
Esto da n4
.
24
180s0.0001d
o n .
1
s
4
0.00075
6.04
Por tanto, n 5 8 (n debe ser par) da la exactitud deseada. (Compare esto con el
ejemplo 2, donde obtuvo n 5 41 para la regla del trapecio y n 5 29 para la regla del
punto medio.) n
EJEMPLO 7
(a) Utilice la regla de Simpson con n 5 10 para aproximar la integral y1
0 ex 2
dx.
(b) Estime el error implicado en esta aproximación.
SOLUCIÓN
(a) Si n 5 10, entonces ∆x 5 0.1 y la regla de Simpson da
y
1
0
ex 2
dx
Dx
3
f fs0d 1 4 fs0.1d 1 2 fs0.2d 1 1 2 fs0.8d 1 4 fs0.9d 1 fs1dg
−
0.1
3
fe0
1 4e0.01
1 2e0.04
1 4e0.09
1 2e0.16
1 4e0.25
1 2e0.36
1 4e0.49
1 2e0.64
1 4e0.81
1 e1
g
1.462681
(b) La cuarta derivada de fsxd − ex 2
es
f s4d
sxd − s12 1 48x2
1 16x4
dex 2
y así, dado que 0 x 1, se tiene
0 f s4d
sxd s12 1 48 1 16de1
− 76e
Por tanto, escribiendo K 5 76e, a 5 0, b 5 1 y n 5 10 en (4), se ve que el error es a
lo más
76es1d5
180s10d4
0.000115
(Compare esto con el ejemplo 3.) Así, con un redondeo a tres decimales, se tiene
y
1
0
ex 2
dx 1.463 n
La figura 10 ilustra los cálculos del
ejemplo 7. Observe que los arcos para-
bólicos son muy cercanos a la gráfica
de y − ex 2
que son prácticamente
indistinguibles de esta.
0
y
x
1
y=ex2
FIGURA 10
Muchas calculadoras y sistemas
algebraicos computacionales tienen un
algoritmo integrado que calcula una
aproximación de una integral definida.
Algunas de estas máquinas utilizan la
regla de Simpson; otras utilizan técnicas
más complejas como la integración
numérica adaptativa. Esto significa que
si una función fluctúa mucho más en
cierta parte del intervalo que en
cualquier otra parte, entonces esta parte
se divide en más subintervalos. Esta
estrategia reduce el número de cálculos
requeridos para lograr la exactitud
prescrita.
h
t
t
p
s
:
/
/
w
w
w
.
j
a
m
a
r
a
n
a
.
c
o
m
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s
_
i
n
f
o
h
t
t
p
s
:
/
/
t
.
m
e
/
u
n
i
v
e
r
s
i
t
a
r
i
o
s

apuntes unidad 2 y 3.pdf

Recomendados

Recomendados

Más contenido relacionado

Similar a apuntes unidad 2 y 3.pdf

Similar a apuntes unidad 2 y 3.pdf (20)

Último

Último (20)

apuntes unidad 2 y 3.pdf