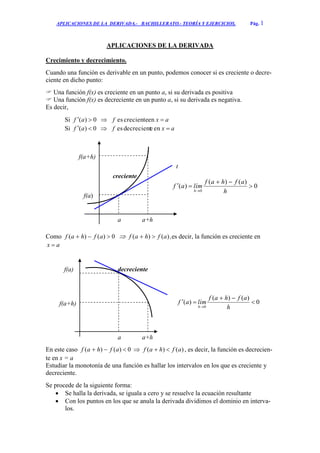
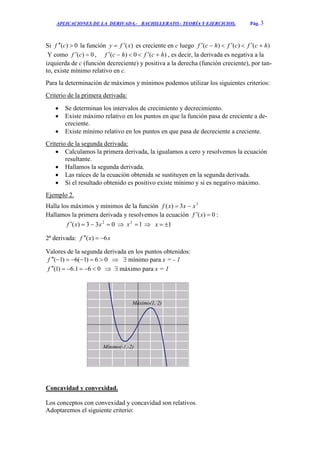
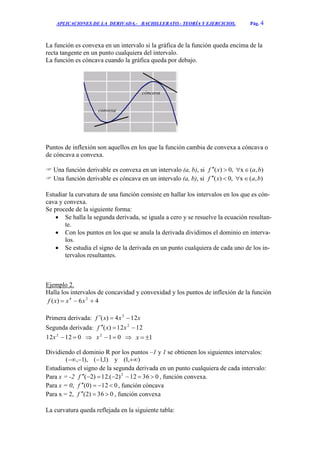
Este documento trata sobre las aplicaciones de la derivada en diferentes conceptos matemáticos. Explica que una función es creciente o decreciente dependiendo del signo de su derivada. También cubre cómo determinar máximos, mínimos, concavidad, convexidad y cómo resolver problemas de optimización usando la derivada. Incluye ejemplos resueltos para ilustrar cada uno de estos conceptos.