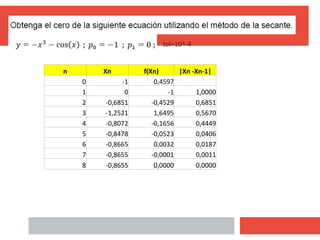
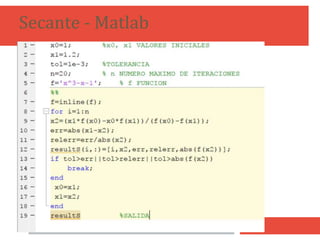
Este documento describe tres métodos numéricos para encontrar las raíces de ecuaciones no lineales: el método de bisección, el método de la regla falsa y el método del punto fijo. Explica los pasos para implementar cada método, incluida la fórmula de recurrencia utilizada para aproximar progresivamente la raíz. También presenta ejemplos numéricos y la implementación en MATLAB de los métodos.

1. MÉTODOS NÚMERICOS PARA ECUACIONES
NO LINEALES
CLASE DE LABORATORIO DE CÁLCULO 4

2. 2
BISECCIÓN
Sea f(x) una función continua en un intervalo [a,b] y sea r
una raíz de la función. Definimos el siguiente algoritmo
que nos permite aproximar la raíz r de f(x).

3. 3
En el nuevo intervalo [a0,b0], con a0=c0, o bien b0=c0 (para
que el intervalo contenga al cero).
Se repite el proceso con n = 1, 2, 3, etc., con lo cual, la
fórmula de recurrencia es cn =(bn+an)/2

4. 4
Pasos para el método de
Bisección
• Paso 1: Elija valores iniciales inferior (a) y
superior (b) que encierren la raíz de forma tal
que la función cambie el signo en el intervalo.
Esto se verifica comprobando que f(a)·f(b) < 0.
• Paso 2: Una aproximación de la raíz c se
determina de
c=(a + b)/2

5. 5
Paso 3: Realice las siguientes evaluaciones para determinar en
que sub-intervalo está la raíz:
•Si f(a)·f(c) < 0
Entonces la raíz se encuentra dentro del sub-intervalo
inferior o izquierdo, por lo tanto, haga b = c y vuelva al paso 2.
• Si f(b)·f(c) < 0
Entonces la raíz se encuentra dentro del sub-intervalo
superior o derecho, por lo tanto, haga a = c y vuelva alpaso 2.
• Si f(c) = 0
Entonces la raíz es igual a c y termina el cálculo.

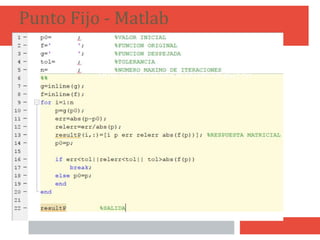
6. 6
f='' ;%función de la cual se desea hallar la raíz
a= ;%extremo inferior del intervalo
b= ;%extremo superior del intervalo
n= ;%numero máximo de iteraciones
tol= ;%tolerancia
%%desarrollo
f=inline(f);%se define como inline a f para poder evaluarla con
%distintos argumentos o parámetros
for i=1:n %se repiten las operaciones como máximo n veces
c=(a+b)/2; %fórmula de recurrencia, aproximación a la raíz
resultB(i,:)=[i a b c abs(f(c))];%se forma una tabla de resultados,
%según lo que pida el ejercicio
if tol>abs(f(c))% si f(c) es casi cero, al menos menor a tolerancia
break % ya no se itera y se muestra resultB
elseif f(c)*f(a)<0 %sino, se verifica hacia donde esta el cero
b=c; %el cero está entre a y c, por tanto se cambia b por c
else a=c; %el cero está entre b y c, por tanto se cambia a por c
end %aca se cierra el if de verificar tol
end %aca se cierra el for de iteraciones
resultB %se despliega una tabla con resultados obtenidos

7. 7
MÉTODO DE REGLA FALSA O
FALSA POSICIÓN
Este método es un mejoramiento de la bisección,
prácticamente se cumplen las mismas condiciones del
método anterior pero con la diferencia de la definición de
la aproximación de la raíz.

8. 8

9. 9
f='' ;%función de la cual se desea hallar la raíz
a= ;%extremo inferior del intervalo
b= ;%extremo superior del intervalo
n= ;%número máximo de iteraciones
tol= ;%tolerancia
%%desarrollo
f=inline(f);%se define como inline a f para poder evaluarla con
%distintos argumentos o parámetros
for i=1:n %se repiten las operaciones como máximo n veces
c=(b*f(a)-a*f(b))/(f(a)-f(b));%fórmula de recurrencia para este método
resultB(i,:)=[i a b c abs(f(c))];%se forma una tabla de resultados,
%según lo que pida el ejercicio
if tol>abs(f(c))% si f(c) es casi cero, al menos menor a tolerancia
break % ya no se itera y se muestra resultB
elseif f(c)*f(a)<0 %sino, se verifica hacia donde esta el cero
b=c; %el cero está entre a y c, por tanto se cambia b por c
else a=c; %el cero está entre b y c, por tanto se cambia a por c
end %acá se cierra el if de verificar tol
end %acá se cierra el for de iteraciones

10. Punto Fijo
Punto fijo 𝑃(𝑥𝑝,𝑥𝑝) de una función y = g(x) es el punto
cuya abscisa 𝑥𝑝 verifica 𝑥𝑝= 𝑔(𝑥𝑝)
Para aproximar a la raíz de la ecuación f(x) = 0 se lo
escribe como x = g(x) y se busca el punto donde la curva
representativa de y = g(x) corta a la recta y = x, para lo
cual se genera la secuencia:
𝑥1=𝑔(𝑥0), 𝑥2=𝑔(𝑥1),⋯,𝑥𝑛=𝑔(𝑥𝑛−1)
que si 𝑔 es elegido convenientemente converge a la raíz
𝑟.
10

11. El método de punto fijo es localmente convergente a 𝑥𝑝
=𝑔(𝑥𝑝) si |𝑔′(𝑥𝑝)|<1
Entendiendo por localmente convergente que existe un
intervalo que contiene a 𝑥𝑝 tal que el método converge
para cualquier valor inicial 𝑥0 que pertenece a dicho
intervalo.
Si |𝑔′(𝑥𝑝)|>1 el método diverge para cualquier valor
inicial 𝑥0. Esto da una guía para la elección de 𝑔.
Punto Fijo - Convergencia
11

12. Ejemplo
1. Tenemos f(𝑥) = 𝑥 ^ 3+4𝑥 ^ 2−10=0
2. Despejamos
3. Derivamos
4. Resolviendo la desigualdad -1 ≤ g’(x) ≤ 1 obtenemos
el rango de valores en los cuales esta el punto fijo.
12

13. El método converge, en cambio otra elección de g podría hacer que no sea
convergente .
5. Con R buscamos la raíz en g(x) , es decir g(R)=R haciendo iteración de las
operaciones.
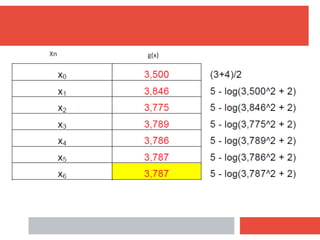
Resolver la ecuación log(x^2 + 2) + x - 5 = 0, con tres cifras decimales de
aproximación, empleando el método de Aproximaciones Sucesivas.
Ejemplo (resolución a mano)
Cambio de signo, hay una raíz en el rango [3-4]
13

14. Despejamos:
g(x)= 5 - log(x^2 + 2) = x
Derivamos:
g'(x)= - 1 / (x^2 + 2) * 2 * x * log e
g'(3,5)= -0,213
Rango en que se encuentra la raiz:
a =3
b =4
Construimos la tabla:
Xn g(Xn)
X0
X1
…
Xn 14

15. Xn g(x)
15

16. Punto Fijo - Matlab
ENTRE COMILLAS SE ESCRIBE LA FUNCION g(x) Y f(x)
16

17. METODO DE NEWTON- RAPHSON
17

18. EJEMPLO
18

19. 19

20. Newton Raphson - Matlab
20

21. SECANTE
Sea la función f(x). Suponiendo que f :R → R, es una función continua y
se conocen los valores de f en 𝑎, y en b.
Para aproximar la raíz r, se parte de dos puntos iniciales (n = 0), de
abscisas p0; p1, se obtiene el punto de intersección, considerando la
ecuación de la recta secante determinada por P0(p0, f(p0)), P1(p1,
f(p1)), (no exige que la cuerda 𝐴𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅
corte al eje 𝑥
21

22. como en el método de la falsa posición que puede escribirse como:
Para y = 0, se tiene, x = p2, con lo cual:
Es la fórmula de aproximación utilizada en la iteración. Haciendo 𝑝1=𝑝
2, 𝑝0=𝑝1 con el nuevo intervalo, se repite el proceso con n = 2, 3, 4,
etc., con lo cual, la fórmula de recurrencia es:
22

23. 23
tol=10^-4
n Xn f(Xn) |Xn -Xn-1|
0 -1 0,4597
1 0 -1 1,0000
2 -0,6851 -0,4529 0,6851
3 -1,2521 1,6495 0,5670
4 -0,8072 -0,1656 0,4449
5 -0,8478 -0,0523 0,0406
6 -0,8665 0,0032 0,0187
7 -0,8655 -0,0001 0,0011
8 -0,8655 0,0000 0,0000

24. Secante - Matlab
24