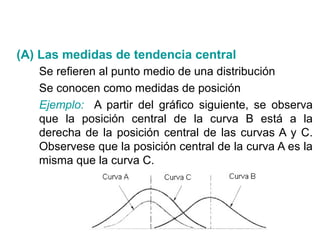
El documento describe diferentes medidas estadísticas para resumir conjuntos de datos, incluyendo medidas de tendencia central como la media, mediana y moda, y medidas de dispersión. Explica cómo calcular e interpretar estas medidas a partir de datos agrupados y no agrupados, y sus propiedades y usos.

1. Tema
55
PROMEDIOS
Un motivo para hacer sospechar
que la Estadística es más un arte
que una ciencia, gira en torno a la
ambigüedad con que se usa el
término “promedio”.

2. 5.1 La estadística de resumen
Después de construir tablas y gráficos, a partir
de una colección de datos, se requieren
medidas más exactas.
La estadística de resumen, proporciona
medidas para describir un conjunto de datos.
Existen tres tipos de medidas de resumen:
• De tendencia central.
• De dispersión.
• De la forma de la distribución.

3. (A) Las medidas de tendencia central
Se refieren al punto medio de una distribución
Se conocen como medidas de posición
Ejemplo: A partir del gráfico siguiente, se observa
que la posición central de la curva B está a la
derecha de la posición central de las curvas A y C.
Observese que la posición central de la curva A es la
misma que la curva C.

4. (B) Las medidas de dispersión
1. Se refieren a la extensión o amplitud de los
datos de una distribución
2. Representan el grado de variabilidad de los
datos.
Ejemplo: Observe que la curva A en el siguiente
gráfico tiene una mayor dispersión que la curva
B, a pesar que la posición central es la misma.

5. (C) Las medidas de la forma de la curva
Las curvas que representan a un conjunto de
datos, pueden ser analizadas de acuerdo a su:
a) Simetría b) Curtósis
Las curvas simétricas, tienen una forma tal que
con una línea vertical que pase por el punto más
alto de la curva, dividirá el área de esta en dos
partes iguales.

6. Las curvas sesgadas son aquellas cuyos valores
están concentrados en el extremo inferior o
superior de la escala de medición del eje
horizontal. La “cola” indica el tipo de sesgo.

7. Cuando medimos la curtósis nos referimos al grado de
agudeza. Pueden ser: leptocúrtica (concentración al
centro) mesocúrtica distribuidos simétricamente) o
platicúrtica (aplanada).

8. 5.2 Propiedades de la sumatoria
1ra
Regla: La suma de los n términos de una serie
constante, es igual a n veces la constante.
∑=
=
n
i
i ncc
1
Ejemplo:
C = 10, n=3
= 10 + 10 + 10 = 3 (10) = 30∑=
3
1i
c

9. 2da
Regla: La suma de los productos de una
constante por una variable, es igual a la constante
multiplicada por la suma de la variable.
∑∑ ==
=
n
i
n
i
i ccx
1
i
1
x
Ejemplo:
C = 5, X1 = 2, X2 = 4, X3 = 6
5(2) + 5(4) + 5(6) = 60
=∑=
3
1i
icx

10. 3ra
Regla: La suma de los valores de una variable más
una constante es igual a la suma de los valores de la
variable más n veces esa constante.
∑ ∑= =
++ =
n
i
n
i ii
ncc
1 1
x)x(
Ejemplo:
C =2, x1 =5, x2 =3, x3 =2
(5 + 2) + (3 + 2) + (2 + 2) = 16
= (5 + 3 + 2) + 3(2) = 16
∑=
=+
3
1
)x( ii
c

11. 5.3 Las medidas de tendencia central
1. En general se denominan promedios.
2. Los más importantes son la media, la mediana y la
moda.
Aritmética
Media Geométrica
Medidas de Mediana Armónica
tendencia central Moda
3. También es útil conocer los percentiles (o fractiles).

12. ¿POR QUÉ SON IMPORTANTES LAS MEDIDAS
DE TENDENCIA CENTRAL?
Porque la mayor parte de los conjuntos de datos
muestran una tendencia a agruparse alrededor de
un dato central.
Las medidas de tendencia central son puntos en
una distribución, los valores medios o centrales
de ésta y nos ayudan a ubicarla dentro de la
escala de medición.

13. 5.3.1 La Media
(A) La media aritmética ( )
a) Obtención: Se obtiene sumando los valores
registrados y dividiéndolos entre el número
de datos.
Ejemplo:
La siguiente tabla muestra el número de
reclamos y quejas presentadas por pacientes en
el Servicio de Emergencias a lo largo de una
semana. Calcule e interprete la media.
Día/Semana Lun Mar Mier Jue Vier Sab
Reclamos/día 8 10 5 12 10 15
x

14. Media aritmética =
= 10 reclamos
b) Interpretación: Si elige al azar un día de la
semana, se espera que los pacientes del servicio
de emergencia realicen 10 reclamos en ese día.
c) Simbología:
Tamaño Media aritmética
Muestra n (equis barra)
Población N µ (mu)
6
60
6
1510125108
=
+++++
x
x

15. d) Cálculos a partir de datos no agrupados, se
utilizan las siguientes formulas.
Para una muestra
donde: : media muestral
: suma de todos los datos
: número de datos (muestra)
n
n
i
i
x
∑
= =1
X
Para una población
donde: µ : media poblacional
: suma de todos los datos
: número de datos (población)
∑ i
X
x
n
∑ i
X
N
N
i
i∑
= =1
X
µ N

16. e) Cálculo a partir de datos agrupados.
El cálculo de la media aritmética, cuando los
datos disponibles se encuentran en tablas de
distribución de frecuencias, se realiza utilizando
la formula siguiente
donde: :media muestral
:frecuencia absoluta de la clase i
:marca de la clase i
∑
∑
=
== n
f
n
f
i
i
i
ii
x
1
1
X
x
if
iX

17. Ejemplo:
La distribución de frecuencias siguiente, representa los
puntajes obtenidos en una evaluación del desempeño,
aplicado al personal técnico de un Centro de Salud. El
puntaje máximo en la prueba es 50. Calcule e interprete en
media.
Desempeño Número de
(puntos) técnicos
12 - 16 4
17 - 21 8
22 - 26 15
27 - 31 23
32 - 36 10
TOTAL 60

18. Primero se calcularán las marcas de clase ( );
es decir, el valor intermedio de cada clase
Marca de Frecuencia
clase ( ) absoluta(fi)
12 - 16 14 4
17 - 21 19 8
22 - 26 24 15
27 - 31 29 23
32 - 36 34 10
Total 60
14(4) + 19 (8) + 24 (15) + 29 (23) + 34 (10)
4 + 8 + 15 + 23 + 10
iX
ix
=x =x
=x
clase
1575
60
26.25

19. Interpretación: Si se elige al azar a un trabajador técnico
de este hospital, se espera que tenga un puntaje de 26,25
en su evaluación de desempeño.
f) La media aritmética ponderada ( )
donde:
= factor de ponderación
= datos∑
∑
=
=
= n
i
i
n
i
ii
w
w
px
1
1
X
px
iw
iX

20. Ejemplo: Una empresa comercializadora de Seguros
Médicos dispone de 3 representantes para la zona de
Miraflores, cada uno de los cuales cobra diferente
comisión por póliza vendida, y realiza diferente número de
contratos. Calcule e interprete el valor medio de la
comisión
Nº de polizas de Comisión
Vendedor Seguro Médico por venta $
Pedro 30 30
Juan 25 40
Pablo 20 50
iw iX

21. Interpretación:
Si se elige al azar un representante se espera que
cobre una comisión de $38.67 por póliza vendida.
67.38$
75
2900
202530
)50(20)40(25)30(30
==
++
++
=px

22. g)Ventajas y desventajas de la media aritmética
Ventajas:
Concepto familiar para muchas personas
Es única para cada conjunto de datos
Es posible comparar medias de diferentes
muestras
Desventajas
Se ve afectada por los datos extremos
Si la muestra es grande y los datos no están
agrupados, su cálculo es tedioso
Si los datos están agrupados en clases con
extremos abiertos, no es posible calcular
la media.

23. (B) La media geométrica ( )
Se utiliza para calcular tasas medias de variación,
como la tasa media de crecimiento poblacional, la
tasa media de inflación mensual, la tasa media de
mortalidad, entre otros.
a) Obtención Se obtiene extrayendo la raíz enésima
del producto de los n valores de una serie.
gx
ng n
x XXXX .........
321
•••=

24. Ejemplo:
La siguiente tabla muestra la tasa de aumento en las
quejas durante los últimos meses. Calcule e interprete la
tasa media mensual.
Meses Enero Febrero Marzo Abril Mayo
Aumento de
quejas
2.6% 5.4% 3.8% 0.5% 1.4%
La tasa 2,6% también se puede expresar como 0,026 , y
puesto que se refiere a un aumento a partir de una base
de 100%, el factor de variación será 1,026. Para los
otros datos se opera igual.

25. Por lo tanto, la media geométrica se
calcula:
5 )014.1)(005.1()038.1()054.1()026.1(=
)(0272540,1 medioocrecimientdeFactor=
5
143903377.1=
100)1( ×−
Tasa media
de variación
=
b) Cálculos
n xxxxxg ,......,, 321=
gx
gx
gx
gx

26. c) Interpretación
Si se selecciona al azar un mes entre enero y
mayo, se espera que las ventas se hayan
incrementado 2.72% con respecto al mes
anterior.
= (1,0272540 - 1) x 100 = 2,72%

27. (C) La media armónica ( )
Se utiliza para calcular el tiempo medio, velocidad
y aceleración media, como por ejemplo, el tiempo
medio para realizar determinada cirugía.
a) Obtención: se obtiene calculando el inverso de
la media aritmética de los inversos de una serie.
hx
n
n
i i
hx
∑
=
= 1
X
1
1

28. Ejemplo:
Los siguientes datos registran el tiempo que utilizan
cuatro médicos al realizar una cierta intervención
quirúrgica. Calcule e interprete el tiempo medio.
Médico A B C D
Tiempo
(minutos)
45 38 52 40
Conocer el tiempo medio permite contar con una
herramienta útil en la planeación de los recursos,
como la Sala de Operaciones. Además de poder
comparar nuestro desempeño con los estándares
de calidad internacionales.

29. b) Interpretación:
Si se selecciona al azar a uno de los cuatro
médicos, se espera que realice este tipo de cirugía
en 43 minutos aproximadamente.
88920
2223171023401976
4
40
1
52
1
38
1
45
1
4
+++
=
+++
=hx
minutos117953.43
8249
889204
==
×
hx
segundos7minutos43=hx

30. 5.3.2 La Mediana
Es la medida que divide en dos subconjuntos
iguales a datos, de tal manera que 50% de los
datos es menor a la mediana y el otro 50% es
mayor a la mediana.
a) Obtención: Se obtiene ordenando la serie de
datos (en forma ascendente o descendente) y
ubicando el dato central.

31. Ejemplo:
Los siguientes datos se refieren al número de
pacientes que llegaron a su cita, después de la hora
programada durante los últimos 11 días en el
Servicio de Pediatría. Calcule e interprete la
mediana.
12, 10, 5, 15, 8, 11, 13, 8, 10, 17, 16
Primero se ordenan lo datos:
5, 8, 8, 10, 10, 11, 12, 13, 15, 16, 17
5 datos menores 5 datos mayores
mediana

32. b) Interpretación: Durante 5 días llegaron menos de 11
pacientes tarde a su cita y durante 5 días, más de 11
pacientes llegaron tarde a su cita.
c) Reglas
1º Si la serie es impar, la mediana ocupa el lugar
central de la serie previamente ordenada.
Ejemplo: 5, 10, 10, 12, 15 , 17, 20, 21, 24

33. Ejemplo:
8, 10, 14, 18, 23, 24, 32, 34
3º Sea la serie par o impar, la mediana ocupa el
lugar ,de la serie previamente ordenada.



 +
2
1n
5.20
2
2318
=
+
=mediana
2º Si la serie es par, la mediana se obtiene de la
semisuma de los dos valores centrales de la serie
previamente ordenada.

34. d) Cálculo a partir de datos agrupados.
donde:
: mediana
: limite real (o frontera) inferior de la clase
mediana.
: número total de datos.
: suma de todas las frecuencias hasta, pero
sin incluir, la clase mediana.
: frecuencia de la clase mediana
: amplitud de clase
( )
c
Mdf
F
n
Md i










+−
+
+=
1
2
1
L
Md
iL
n
F
Mdf
c

35. Ejemplo: La tabla siguiente muestra la experiencia
laboral (años) del personal de seguridad que labora en
un gran hospital. Calcule e interprete la mediana.
Experiencia Número de
laboral trabajadores
(años) de seguridad
0 - 3 4
4 - 7 12
Clase
Mediana
8 - 11 24
12 - 15 16
16 - 19 10
20 - 23 3
69
Lugar de la mediana:
4
24
)16(
2
169
5,7









 −
+
+=dM
4
24
1635
5,7



 −
+=
Mediana = 10,5 años
o
35
2
169
2
1
=
+
=
+n

36. Interpretación:
La mitad del personal de seguridad que
labora en este hospital tienen una experiencia
laboral igual o menor a 10 años 6 meses. La
otra mitad de este personal tiene una
experiencia laboral igual o mayor a 10 años y
6 meses.

37. e) Ventajas y desventajas
Ventajas:
Los valores extremos no afectan a la mediana
como en el caso de la media aritmética.
Es fácil de calcular, interpretar y entender.
Se puede determinar para datos cualitativos,
registrados bajo una escala ordinal.
Desventajas:
Como valor central, se debe ordenar primero la
serie de datos.
Para una serie amplia de datos no agrupados, el
proceso de ordenamiento de los datos demanda
tiempo y usualmente provoca equivocaciones.

38. 5.3.3 La Moda
La moda es el valor que más se repite dentro de un
conjunto de datos.
a) Obtención: se obtiene organizando la serie de
datos y seleccionando el o los datos que más se
repiten.
4, 5, 7, 8, 8 , 10, 12, 15
4, 7, 12,12 , 15, 16, 20, 20 , 24, 27
7, 12, 15, 18, 25, 30, 31, 38
Ejemplo:

39. b) Cálculo a partir de datos agrupados
donde:
: moda
: limite real (o frontera) inferior de la clase
modal (la de mayor frecuencia)
: frecuencia de la clase modal menos la
frecuencia de la clase anterior
: frecuencia de la clase modal menos la
frecuencia de la clase siguiente
: amplitud de clase
c
i 





∆+∆
∆
+=
21
1
LoM
oM
i
L
1
∆
2
∆
c

40. Las clases mediana y modal pueden coincidir pero
conceptualmente son diferentes.
Ejemplo: La tabla siguiente muestra los errores de
facturación durante un mes, en una Clínica. Calcule e
interprete la moda.
Interpretación: Durante un mes, el número más frecuente
de errores de facturación en esta clínica es 6.
Errores de
facturación Días
0 - 3 6
4 - 7 12
Clase
Modal
8 - 11 8
12 - 15 3
16 - 19 1
Total 30
Clase moda : (4 - 7)
Mo = 5,9
6
1
=∆
4
2
=∆ 4
46
6
5.3Mo 





+
+=

41. e) Ventajas y desventajas de la moda.
Ventajas:
Se puede utilizar tanto para datos cualitativos
como cuantitativos.
No se ve afectada por los valores extremos.
Se puede calcular, a pesar de que existan una o
más clases abiertas.
Desventajas:
No tiene un uso tan frecuente como la media.
Muchas veces no existe moda (distribución
amodal).
En otros casos la distribución tiene varias
modas, lo que dificulta su interpretación.

42. 5.3.4 Los Percentiles
Son los valores que dividen en 100 partes iguales
a un conjunto de datos
a) Cálculo: para datos agrupados.
( )
c
f
n
iK










+
+−
=
K
P
1
i
F
100
K
LP

43. donde:
: percentil
: el percentil buscado
: número de datos
: frecuencia acumulativa hasta la clase
anterior a la clase donde se ubica el percentil K
: frecuencia absoluta de la clase donde se ubica
el percentil K
: amplitud de clase
K
P
c
K
n
iF
K
f
P

44. Ejemplo:
La tabla muestra la experiencia (en años) de las
enfermeras de un gran centro hospitalario
Experiencia Trabajadores
(años)
0 - 3 18
4 - 7 42
8 - 11 68
12 - 15 120
16 - 19 40
20 - 23 34
24 - 27 12
Total 334

45. ¿Sobre qué edad se ubica el 25% de las enfermeras de
mayor experiencia?
Para saber en cuál clase se halla este dato, se
calculó la frecuencia acumulativa.
Menor
Experiencia
Mayor
Experiencia
75 % 25 %
P75
K = 75
)ordenadosnúmeroslosde(5,250
100
)334(75
100
Kn
PdelLugar o
75 ===

46. Experiencia Nº Trabajadores Frec. Acumulada
(años)
0 - 3 18 18
4 - 7 42 60
8 - 11 68 128
12 - 15 120 248
16 - 19 40 288
20 - 23 34 322
24 - 27 12 334
334
Interpretación: Para que una enfermera esté
comprendida dentro del 25% de mayor experiencia
laboral debe tener al menos 15 años, 7 meses y 24
días.
( )
4
40
1248
100
75(334)
5.15
75
P









 +−
+= años65.15
75
P =
iFif
En esta clase
se localizan del
249º - 288º
F=248

47. Algunas personas
sueñan con
alcanzar grandes logros...
mientras que otros
permanecen despiertos
y los realizan!