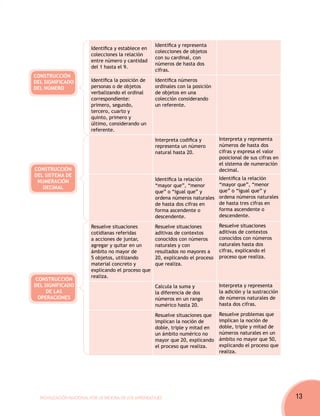
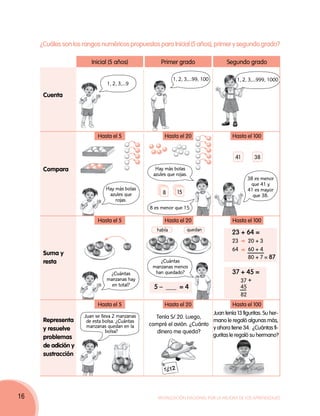
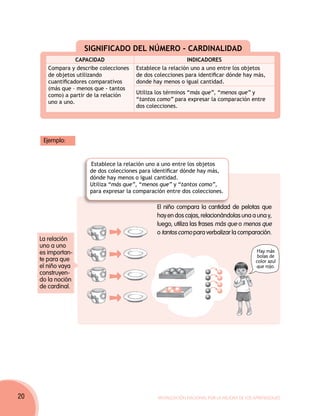
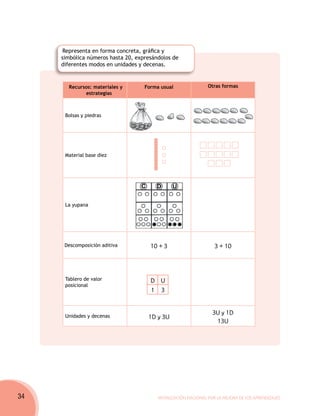
Este documento presenta un debate sobre diferentes enfoques del aprendizaje de matemáticas. Describe dos casos de actividades docentes para enseñar nociones de doble y triple a niños de segundo grado. En el primer caso, la maestra Josefina propone copiar tablas de multiplicar, mientras que en el segundo caso, la maestra Alicia propone una actividad con material concreto. El documento sugiere que el enfoque de Josefina se centra en la memorización mientras que el de Alicia facilita la comprensión a través de la experiencia concre