1. El documento describe las propiedades del electrón y las interacciones entre electrones y fotones. Explica cómo los electrones pueden ser extraídos de un material mediante calentamiento, campo eléctrico, emisión secundaria o efecto fotoeléctrico. 2. La teoría cuántica explica el efecto fotoeléctrico al proponer que la luz está compuesta de partículas llamadas fotones, cada uno con una energía proporcional a su frecuencia. 3. Los fotones pueden interact

1. 1
El electrón y el fotón
Partícula cargada responsable de la mayoría de los fenómenos
observados por ser el componente más externo del átomo
• determina las propiedades químicas de los materiales debido a
que es responsable de los enlaces átomicos (moléculas, sólidos,
etc)
• puede saltar de un átomo a otro generando corrientes eléctricas
Características
me=9.11x 10-31 [kg] → mec2=0.511 [MeV]
e=-1.6x 10-19 [C]
Las cargas observadas en la naturaleza son siempre múltiplos de
esta cantidad. Q= e.n (n=0, ±1, ±2, ....)
Que fuerzas actúan sobre el electrón?
+
N
e-r
Fuerza eléctrica FE= k e.qN / r2
Fuerza gravitatoria FG= G me.mN / r2
FG G me.mN / r2
FE k e.qN / r2
= ∼ G me.mN
k e2
∼ 6x 10-11x 10-30x 10-27
9x 109x (1.6x 10-19)2
∼ 10-40
La fuerza gravitatoria es despreciable frente a la eléctrica !!!
El electrón
1
Como sacar los electrones de un material?
Electrones en un material conductor (por ejemplo un metal sólido)
Material Exterior
+ + + +
+ + + +
+ + + +
• Los electrones internos son atraídos
por fuerzas eléctricas de todas
direcciones y pueden desplazarse
• En cambio los electrones que salen
son atraídos hacia el interior del
material ⇒ hay que entregarles
energía para sacarlos, solos no salen
del material
Diagrama de energía de un electrón en un sólido
Epdentro< Epfuera ⇒
e ligado
Además los
electrones tienen
energía cinética Ek
El electrón con mayor energía dentro del material necesita una
energía (eΦ) para sacarlo del material
eΦ: función de trabajo (de unos pocos eV para metales) 2

2. 2
Para sacar los electrones del material hay que:
• entregarle al menos una energía eΦ a los electrones
• o hay que modificar la energía potencial (por ejemplo
agregando un campo eléctrico externo E), atrayendo a los
electrones desde fuera.
Métodos para sacar un electrón de un material
1) Agregando campo externo E
Se puede pero se requieren campos eléctricos muy grandes: Φ∼
1V y ∆x∼ 1A=10-10 m, entonces se requieren campos del orden de
1010 V/m (campo enorme!!!)
E
dEp/dx=Eext
3
2) Calentando el material (Emisión termoiónica)
Al aumentar la temperatura del metal se aumenta la energía
cinética de los electrones del material.
Para ver cómo es la energía cinética de los electrones en
función de la temperatura podemos modelar a los electrones del
sólido como si fueran un gas de electrones libres. Esto no es
exacto pero nos permite hacer una estimación de la energías
cinéticas
Entonces si los electrones se comportan como un gas de
electrones libres, satisfacen una distribución de energías
cinéticas del tipo Maxwell-Boltzmann
T=300 K
T=1000 K
eΦ
n(Ek
)
Ek
Si T=300 K, n(Ek=eΦ) ∼ N0.10-40
Muy pocos electrones
Si T=1000 K, n(Ek=eΦ) ∼ N0.10-1
Una fracción considerable de
electrones
N0: número de electrones del gas
K: constante de Boltzmann
Número de electrones con
energías entre Ek y Ek+dEk
4

3. 3
Entonces: calentando el material es posibles extraerle
algunos electrones
Ejemplo: Tubo de rayos catódicos (Televisor)
El cátodo se
calienta
(resistencia)
y emite
electrones
Electrones
que son
acelerados en
dirección al
ánodo lo
atraviesan
Con campos
eléctricos y
magnéticos es
posible
deflectar el haz
de electrrones
La pantalla
fluorescente
emite luz al
recibir el
impacto de
los electrones
5
3) Emisión secundaria
Un electrón de alta energía penetra en el material y entrega su
energía a otros electrones que pueden escapar del material
Ejemplo: tubo amplificador: * fotomultiplicador (incide luz)
* electromultiplicador (incide un e-)
La luz también puede arrancar electrones de un material!!!
Luz o electrones inciden
en el cátodo y arrancan
más electrones
6

4. 4
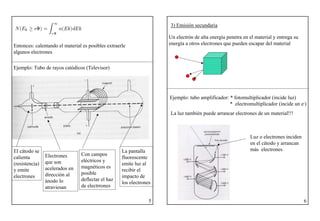
4) Efecto fotoeléctrico (emisión de electrones con luz)
observaciones del efecto:
• Sólo algunos materiales (eΦ < 1eV) emiten con luz visible,
aunque todos emiten calentándolos!
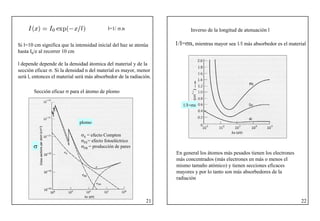
• Si la luz tiene una frecuencia menor que una cierta frecuencia
umbral fc el material no emite (Si f <fc)
• Si f > fc la emisión de electrones es inmediata, independiente de
la intensidad de la luz
• La energía cinética Ek con que salen los electrones dependen de
la frecuencia f de la luz y no de su intensidad
• La corriente de electrones que salen es independiente de la
frecuencia f y aumenta con la intensidad
Pero la teoría clásica (ondulatoria) de la luz predice algo distinto:
• La energía cinética de los electrones debería depender
primordialmente de la intensidad de la luz (la energía se va
entregando continuamente) y no de la frecuencia f
• Si el haz es de baja intensidad, la energía se va acumulando
hasta que al final algún electrón logre salir
Cual es el motivo de esta discrepancia ?
7
Explicación cuántica del efecto fotoeléctrico
El fotón
Inspirado en la explicación de Planck de la radiación de cuerpo
negro, Einstein propuso (Premio Nobel en 1921 por esto) que la
luz se transfiere en cuantos (paquetes) de energía bien definida
proporcional a la frecuencia de la luz. Estos “cuantos” se
denominan fotones y la luz se comporta como si fuera un flujo de
fotones
E=hν
h=6.63 x 10-34 [J.s] contante de Planck
ν =frecuencia de la luz
Energía de un fotón
Entonces el efecto fotoeléctrico se explica de la siguiente
manera:
γ
hν
Ek
e-
Si el fotón tiene suficiente energía saca al electrón del material
y si no, no saca ningún electrón. No hay acumulación.
8

5. 5
hν = Ekmax + eΦ
La frecuencia umbral es cuando le entrega la energía justa para
escapar del material y sale con energía cinética Ek=0
hνc = eΦ
Ek
9
hν = Ekmax + eΦ
hν = eV + eΦ
ν = (e/h)V + (e/h)Φ
ν
V
νc
Pendiente=e/h Como e lo conozco de otro
experimento (Millikan) puedo
obtener h y Φ
Se puede medir h y Φ con el siguiente experimento
El V inverso tiende a frenar a los electrones que salen, sólo van a
producir corriente aquellos electrones que salgan con Ek >eV
Entonces podemos medir Ekmax ajustando V hasta que la
corriente del circuito se haga cero y repetir para varias
frecuencias ν de la luz incidente
V
10

6. 6
Si repito el experimento con otros materiales obtengo otros
valores de Φ pero el mismo valor de h, h está asociado al cuanto
de luz y no al material.
Conclusión
La luz es una onda electromagnética pero su energía aparece en
paquetes o cuantos bien definidos llamados fotones
El fotón tiene una energía E=hν donde ν es la frecuencia de la
onda electromagnética y viaja con la velocidad de la luz.
mfotón=0 ⇒ E=pc
v=c
p= E/c = hν/c = h/λ
p=h/λ=(h/2π) k
El momentum de la onda también está cuantizado
Entonces en que quedamos? la luz es una onda o son partículas ?
Es ambas cosas a la vez (dualidad onda-partícula) se transporta
como una onda (interferencia y difracción) pero entrega su
energía como si se tratara de un flujo de partículas (fotones).
Pero lo mismo le ocurre a las partículas de materia como los
electrones (lo veremos más adelante)
11
La intensidad de la onda es proporcional al flujo de fotones
I=(hν).(densidad de flujo de fotones)
Resumiendo el efecto fotoeléctrico se explica así:
• un solo fotón entrega su energía (hν) a un solo electrón, si es
mayor que eΦ el electrón logra escapar del material
• La corriente de electrones que se obtiene ∼ flujo de electrones
∼ flujo de fotones ∼ Intensidad de la luz
Otro proceso similar (fotoionización)
Este proceso ocurre cuando la luz incide en átomos libres (gas)
+
e-
hν
+
Que energía debe tener ahora el fotón? En el caso del átomo de
hidrógeno debo entregarle 13.6 eV al electrón para que escape
del núcleo.
ν=13.6 eV/h =3.28 1015 Hz (λ=91 nm → radiación ultravioleta)
12

7. 7
Tipos de interacción de fotones con la materia (electrones)
1) Efecto fotoeléctrico : electrones arrancado de un metal al
incidir luz. El fotón es absorbido por un electrón que escapa
del material venciendo a la función trabajo. Este proceso
sólo ocurre en electrones en materiales, no en electrones
libres.
2) Efecto Compton: (Arthur Compton 1923, Nobel en 1927)
ocurre con fotones muy energéticos
Como la energía del fotón es mucho mayor que la
energía de enlace del electrón, el fotón “ve” al electrón
como si estuviera libre en el choque.
El resultado que se obtiene de este proceso es que el fotón
dispersado tiene una frecuencia menor que la del fotón
original (esto sería imposible con la teoría clásica de la
radiación)
Clásicamente si uno incide con una onda de frecuencia ν,
debido a los campos el electrón oscila con frecuencia ν,
entonces la radiación emitida por el electrón también
tendrá frecuencia ν
Colisión libre γ+e- → γ+e-
13
Conservación de energía y
momentum
p=h/λ
momentum del fotón
Introduciendo pe
2 en
la fórmula anterior
14

8. 8
(h/me.c)=longitud de onda de Compton=λc ≈ 2.4 x 10-12 m
Si λ >>λc, ∆λ se hace muy pequeño comparado con λ y el
efecto Compton no se distingue
Fuente de rayos X
Electrón
del gas
Haz dispersadoHaz incidente
Detalle del experimento y resultado
Se observa la longitud de onda de la
radiación dispersada un ángulo θ
15
3) Producción de pares partícula-antipartícula
Ocurre en presencia de un material o átomo pesado. El fotón se
convierte en un par electrón-positrón
e-
e+
hν
El balance energético del proceso es el siguiente:
Eγ = Ee++ Ee-
La mínima energía que debe tener el fotón para poder crear un
electrón y un positrón es la energía de reposo de ambas partículas
o sea 2.me.c2 = 1.02 MeV (λ=0.012 A=radiación gamma)
Cámara de burbuja: Los espirales corresponden a las trayectorias
de un electrón creados en un punto
16

9. 9
4) Aniquilación de pares
Es el proceso inverso al anterior, un electrón y un positrón dan
lugar a fotones
e- + e+ → 2γ
Es necesario que se generen dos fotones para que se conserve
el momentum del proceso
5) Bremsstrahlung (radiación de frenado)
Si el electrón se frena bruscamente al chocar en un material la
aceleración genera radiación electromagnética
Ejemplo: Máquina para generar rayos X
Clásicamente uno debería obtener un espectro
de radiación continuo en todas las longitudes de
onda λ
17
En realidad existe una longitud de onda mínima λmin (o una
frecuencia máxima νmax) que depende de la energía de los
electrones que chocan
Ek’-Ek = hν
La frecuencia máxima será si la energía cinética final Ek’ es cero
hνmax =Ek ⇒ νmax=Ek/h ⇒ λmin=c/νmax
λ (A)
Intensidad de la
radiación para
distintas energías de
los electrones
incidentes
18

10. 10
Absorción de fotones en un material
Cuando un haz de fotones penetra en un material el haz se va
atenuando debido a la interacción de los fotones con los
electrones del material fundamentalmente y con los núcleos
Los choques y absorciones de fotones son debidos
principalementes a tres procesos:
a) Efecto fotoeléctrico (más importante a bajas energías del
fotón)
b) Efecto Compton (más importante a energías intermedias)
c) Producción de pares (cuando la energía del fotón es muy
alta)
Sea la sección eficaz de choque σ : área promedio de blanco que
presenta un electrón que va a chocar con el fotón
σ
Si el fotón cruza el área σ hay choque
Si pasa fuera del área σ no hay choque
19
Sea n el número de átomos por unidad de volumen (densidad
atómica)
A
dx
En un trozo de área A y espesor dx hay en
promedio n.A.dx átomos
El área total ofrecida como blanco a través del área A es:
σ.(n.A.dx)
La fracción del área A que es ofrecida como blanco es:
σ.(n.A.dx)/A=σ.n.dx
Si hay N fotones incidiendo en el área A, los que logran chocar
en el tramo dx son: N.(σ.n.dx), entonces del otro lado de los N
fotones originales van a pasar: N- N.(σ.n.dx)
Entonces: N(x+dx)=N(x)-N(x). σ.n.dx
⇒
Como la intensidad del haz es proporcional al número de fotones
Entonces:
A l=1/ σ.n se le denomina longitud de atenuación o camino
libre medio
20

11. 11
l=1/ σ.n
Si l=10 cm significa que la intensidad inicial del haz se atenúa
hasta I0/e al recorrer 10 cm
l depende depende de la densidad átomica del material y de la
sección eficaz σ. Si la densidad n del material es mayor, menor
será l, entonces el material será más absorbedor de la radiación.
plomo
σ
Sección eficaz σ para el átomo de plomo
σS = efecto Compton
σPE= efecto fotoeléctrico
σPR = producción de pares
21
1/l=σn
Inverso de la longitud de atenuación l
1/l=σn, mientras mayor sea 1/l más absorbedor es el material
En general los átomos más pesados tienen los electrones
más concentrados (más electrones en más o menos el
mismo tamaño atómico) y tienen secciones eficaces
mayores y por lo tanto son más absorbedores de la
radiación
22

12. 12
Ejemplo: radiografías de rayos X. El hueso contiene calcio
(Ca) y absorbe más rayos X que la carne (C,N,H,O). Entonces
cuando uno hace pasar rayos X por el cuerpo se ve la sombra
de los huesos en la placa fotográfica. En el esquema el anillo
de oro absorbe aún más que el hueso.
La energía de los rayos X varía de 1 keV hasta 10 keV
23