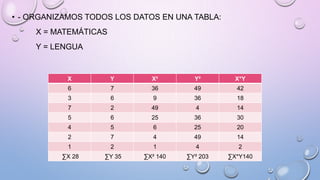
El documento describe un estudio que examina si existe una correlación entre las calificaciones de matemáticas y lenguaje de una muestra de estudiantes. Se proporcionan los datos de las calificaciones de la muestra en una tabla. El documento indica que se debe calcular el coeficiente de correlación de Pearson para determinar si existe una correlación significativa entre las dos variables en la población de la que proviene la muestra.

1. 3. DE UNA MUESTRA DE ALUMNOS CONOCEMOS LAS NOTAS DE
MATEMÁTICAS (X) Y DE LENGUA (Y), SEGÚN LOS RESULTADOS DE LA
TABLA. SI AMBAS VARIABLES SE DISTRIBUYEN NORMALMENTE,
AVERIGUAR ¿EXISTE CORRELACIÓN ENTRE AMBAS VARIABLES EN
LA POBLACIÓN DE DONDE PROVIENE LA MUESTRA?
• TENEMOS DOS VARIABLES CUANTITATIVAS “NOTA DE
MATEMÁTICAS” Y “NOTA DE LENGUA” QUE SE DISTRIBUYEN
NORMALMENTE, POR LO QUE TENEMOS QUE:
• 1. CALCULAR EL COEFICIENTE DE CORRELACIÓN DE PEARSON
• 2. AVERIGUAR SI EL COEFICIENTE DE CORRELACIÓN ES
SIGNIFICATIVO

2. • - ORGANIZAMOS TODOS LOS DATOS EN UNA TABLA:
X = MATEMÁTICAS
Y = LENGUA
X Y X² Y² X*Y
6 7 36 49 42
3 6 9 36 18
7 2 49 4 14
5 6 25 36 30
4 5 6 25 20
2 7 4 49 14
1 2 1 4 2
∑X 28 ∑Y 35 ∑X² 140 ∑Y² 203 ∑X*Y140

3. - CALCULAR EL COEFICIENTE DE CORRELACIÓN DE PEARSON ENTRE X E Y,
MEDIANTE LA FÓRMULA:
AL DAR EL RESULTADO 0, QUIERE DECIR QUE NO EXISTE CORRELACIÓN ENTRE LAS NOTAS
DE MATEMÁTICAS Y LENGUA, POR LO QUE NO PODEMOS SEGUIR CON EL EJERCICIO.