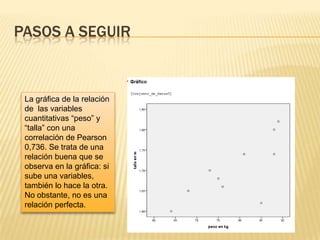
Este documento presenta varios ejercicios sobre correlación utilizando SPSS. El primer ejercicio muestra una correlación moderada y positiva entre el peso y las horas dedicadas al deporte. El segundo ejercicio encuentra una correlación casi perfecta e inversa entre el número de cigarrillos fumados y las notas de acceso. El tercer ejercicio muestra una correlación positiva alta entre el peso y la edad en una muestra de niños.























![3. SE REALIZA EL CONTRASTE DE DE HIPÓTESIS DE RXY
tn-2= 0,91 [(21-2)/1- 0,912]= 0,91 110,5293=
0,91[10,5132]= 9,567
El valor tn-2 se compara con el valor del punto crítico
obtenido en la tabla t de Student, con un grado de
libertad 19 (n-2) y un nivel de significación =0,05:
t0,05;19=2,093
Como tn-2 tn-2; se rechaza la Ho y se acepta H1con un
riesgo de equivocarnos de 0,05, y significa que en la
población la correlación es distinta de 0, por lo que existe
asociación lineal entre las variables “edad” y “peso” con
una correlación muy positiva. Eso quiere decir que ambas
variables están relacionadas en la población.](https://image.slidesharecdn.com/seminario-130530120415-phpapp01/85/Seminario-26-320.jpg)





