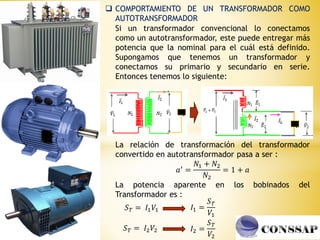
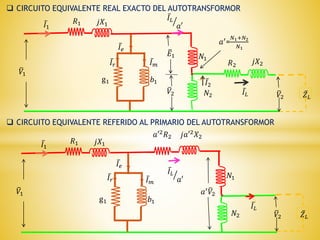
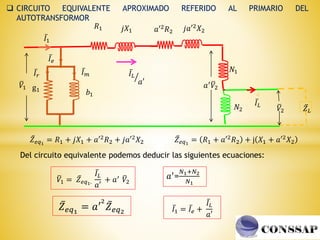
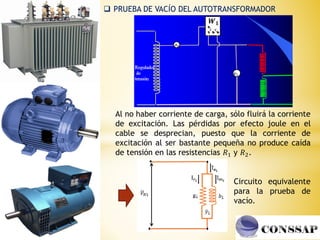
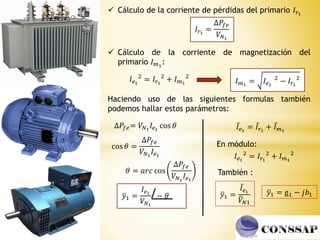
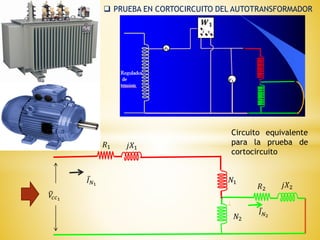
Los autotransformadores son dispositivos que combinan arrollamientos primarios y secundarios en serie, permitiendo la regulación de voltajes y eficiencia en sistemas eléctricos. Aunque ofrecen ventajas como menor tamaño y costo, presentan desventajas significativas, incluida la conexión eléctrica entre los bobinados que limita su uso. Se utilizan principalmente como reguladores de tensión y en el arranque de motores eléctricos de inducción.