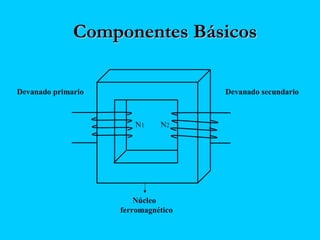
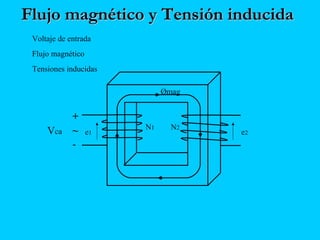
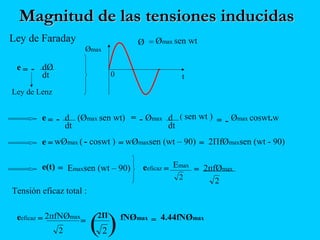
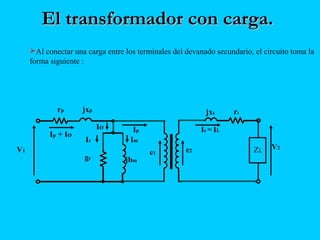
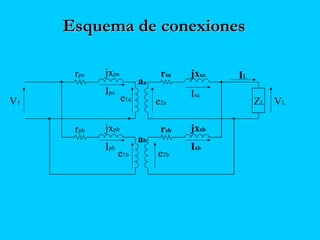
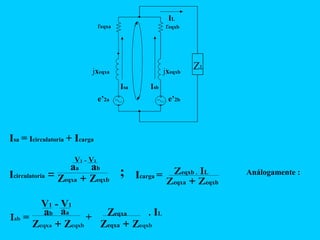
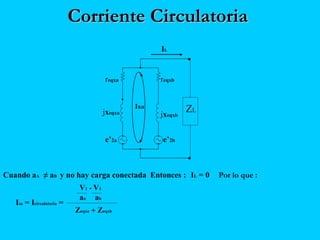
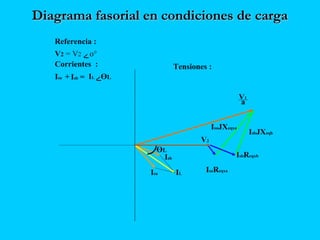
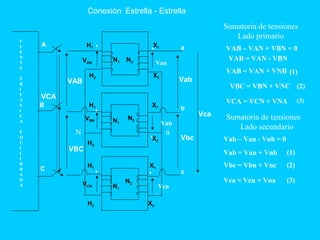
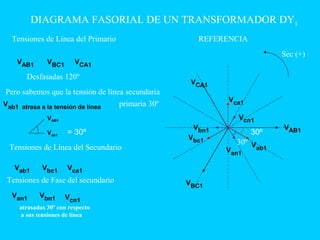
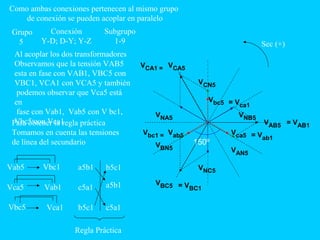
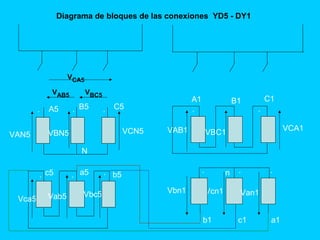
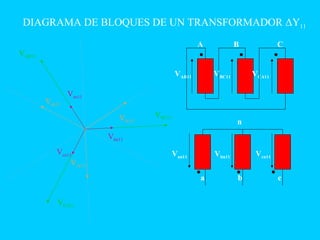
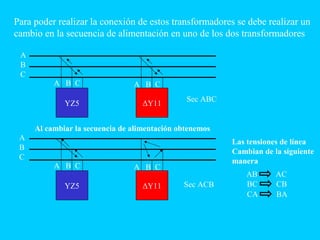
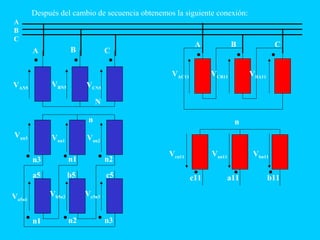
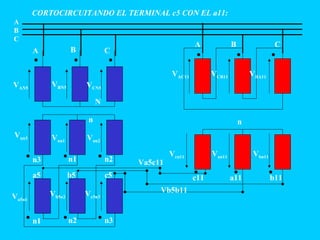
El documento describe el funcionamiento del transformador monofásico, el cual transforma energía eléctrica de un circuito a otro mediante una transformación magnética. Consta de dos bobinas enrolladas alrededor de un núcleo ferromagnético que no están conectadas directamente, sino que comparten un flujo magnético común. Un devanado se conecta a la fuente de entrada y el otro suministra energía a las cargas.