Este documento explica los conceptos básicos de los arreglos y matrices en PseInt. Define un arreglo como una estructura homogénea que almacena múltiples elementos del mismo tipo de forma consecutiva en memoria. Explica que los arreglos unidimensionales se conocen como vectores y los bidimensionales como matrices. Proporciona ejemplos de código para crear y manipular arreglos y matrices, como sumar los elementos de un arreglo o llenar una matriz con valores ingresados por el usuario.

1. Arreglos
Algoritmos Computacionales y
Programación
1

2. 3 6 8 1 0 4 2
0 1 2 3 4 5 6
Ejemplo de un arreglo que contiene 7 números enteros
índices
Elementos del
arreglo
Elemento que ocupa la
posición 3 en el arreglo
• Un arreglo es una estructura homogénea, compuesta
por varios elementos, todos del mismo tipo y
almacenados consecutivamente en memoria.
Arreglo unidimensional o Vector
2

3. • Cada arreglo o vector posee un índice (empieza en 0)
que indica la posición en la que está almacenado un
elemento, esto se debe a que el arreglo está
segmentado.
3

4. • Existen distintos tipos de arreglos dependiendo
del tipo de dato que contengan. Ejemplos:
• Arreglo numérico.
• Arreglo de caracteres.
a b c
1 3 5 7

5. Arreglo bidimensional o Matriz
• MATRIZ o arreglo bidimensional es un arreglo de
arreglos, que representan una tabla, tiene filas y
columnas.
• Los datos de una matriz son todos del mismo tipo y
son accedidos mediante dos índices o posiciones:
– uno para filas y otro para columnas.
• Por ejemplo:
0 1 2
0 (0,0) (0,1) (0,2)
1 (1,0) (1,1) (1,2)
2 (2,0) (2,1) (2,2)
Filas
columnas

6. Arreglos en PseInt
• PALABRAS CLAVE: Dimension
• Dimension: Son conocidos como arreglos o
matrices, aquellos de una sola dimensión se
llaman arreglos y los bidimensionales son
matrices.
• Estos son espacios fraccionados utilizando una
sola variable, cada espacio es un subíndice que
permite recorrer el vector o la matriz por medio
de un ciclo repetitivo (Para).
6

7. Arreglos en PseInt
• Sintaxis para crear un vector:
Dimension identificador [tamaño];
• Sintaxis para crear una matriz:
Dimension identificador [filas,columnas];
7

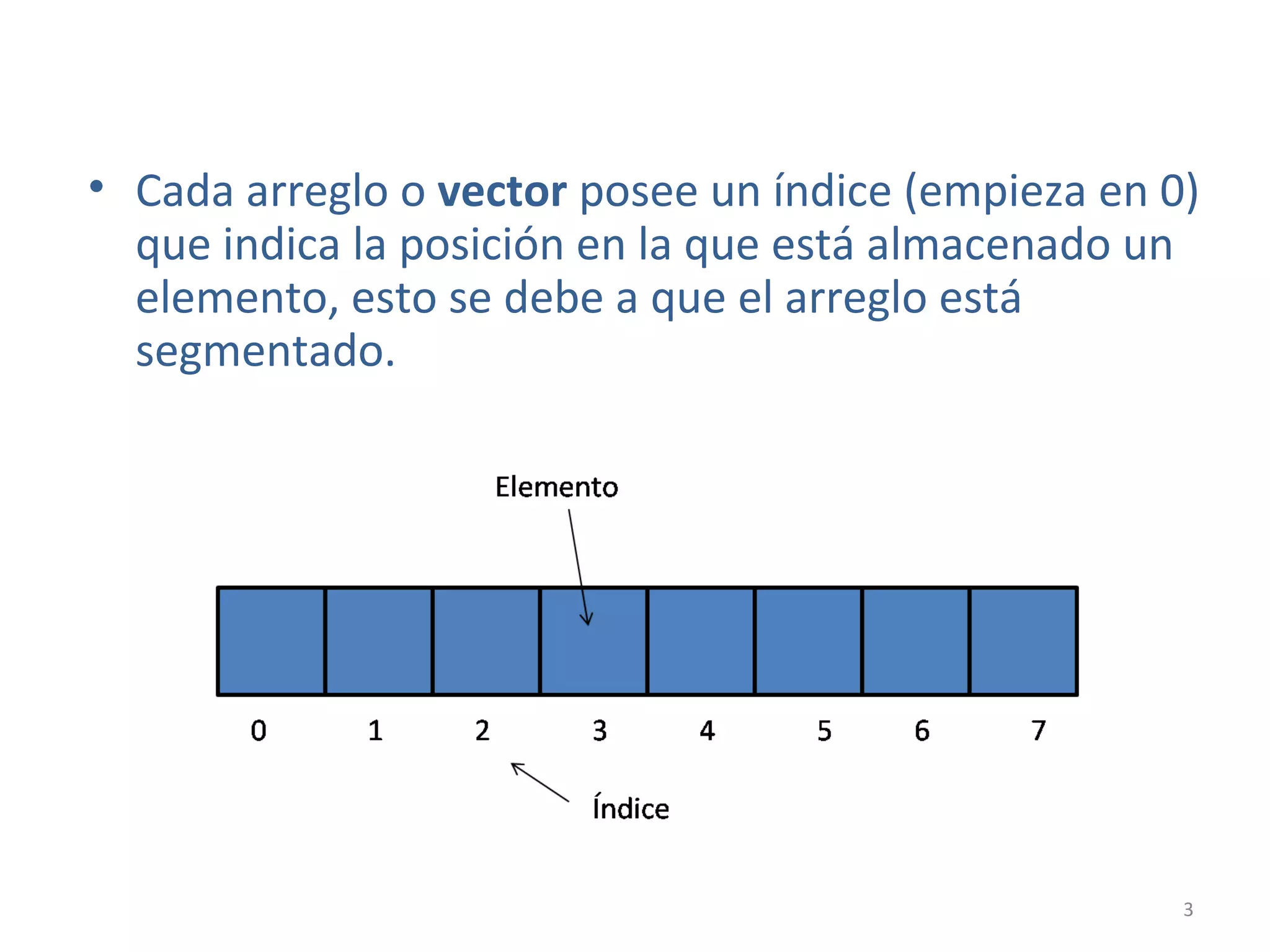
8. PSEINT – Arreglos
En Pseint la sentencia para poder definir un arreglo es la siguiente:
Dimension <identificador>[tamaño]
Otro ejemplo:
Dimension Lista[9]
Para poder acceder a un elemento del arreglo se utiliza el siguiente comando:
<identificador>[posición_elemento]
Ej: Lista[0] ,esto va a devolver el elemento en la posición 0.
0 1 2 3 4 5 6 7 8

9. Ejemplo 1
• Crear un arreglo llamado num que almacene
los siguientes datos: 20, 14, 8, 0, 5, 19 y 24.

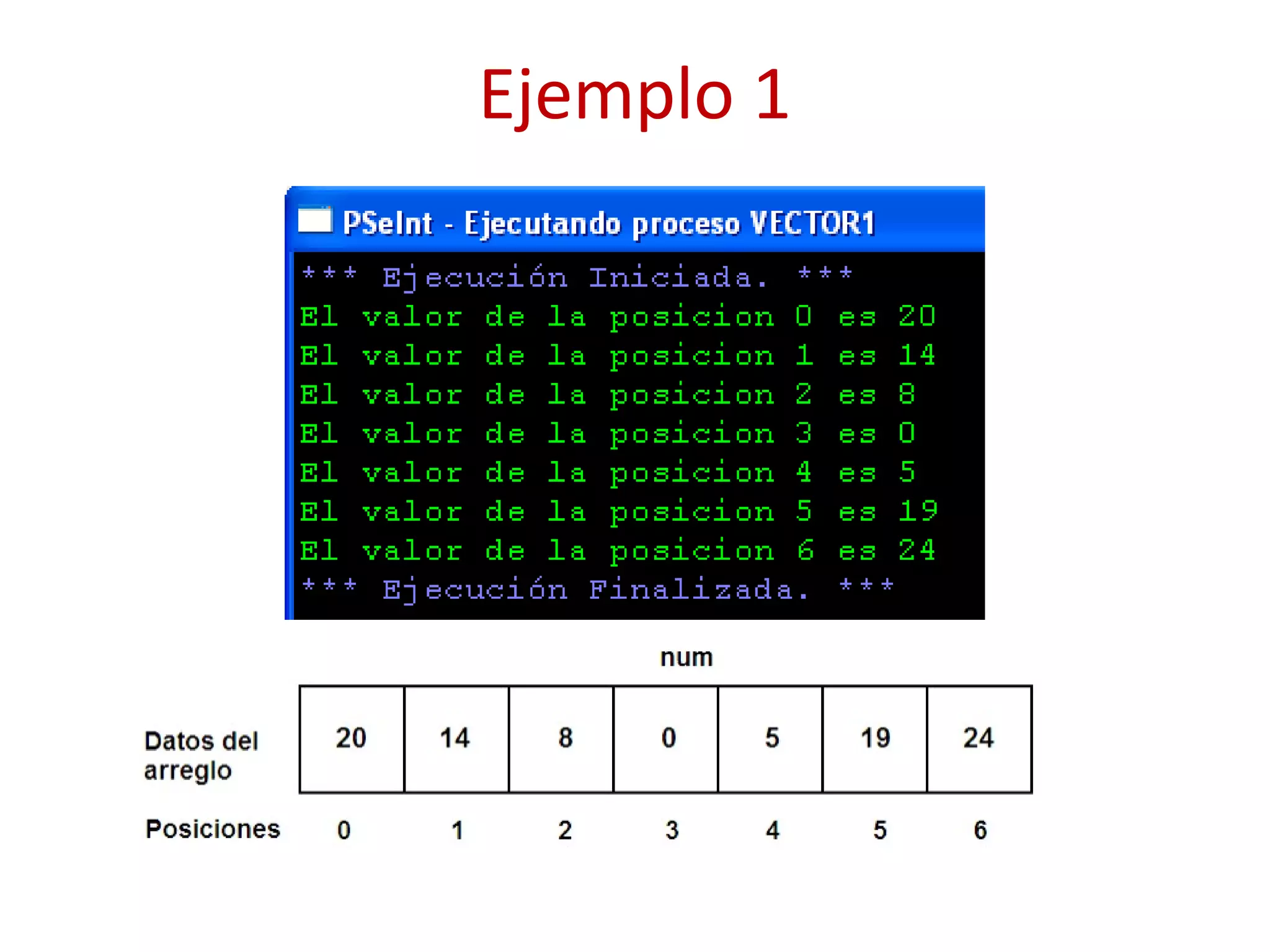
10. Ejemplo 1
Algoritmo vector1
Inicio
Definir num Como Entero
Dimension num[7];
num[0]<-20;
num[1]<-14;
num[2]<-8;
num[3]<-0;
num[4]<-5;
num[5]<-19;
num[6]<-24;
Escribir "El valor de la posicion 0 es ",num[0];
Escribir "El valor de la posicion 1 es ",num[1];
Escribir "El valor de la posicion 2 es ",num[2];
Escribir "El valor de la posicion 3 es ",num[3];
Escribir "El valor de la posicion 4 es ",num[4];
Escribir "El valor de la posicion 5 es ",num[5];
Escribir "El valor de la posicion 6 es ",num[6];
Fin

11. Ejemplo 1

12. • Al utilizar arreglos en base cero los elementos validos
van de 0 a n-1, donde n es el tamaño del arreglo.
• En el ejemplo 1 las posiciones del arreglo num
entonces van desde 0 a 7-1, es decir de 0 a 6.
• Los ciclos, también conocidos como bucles o
estructuras de control repetitivas, juegan un papel
muy importante en los arreglos.
• En el anterior ejemplo, imprimimos los datos a través
de siete mensajes, una tarea que lleva cierto tiempo y
más cuando la cantidad de datos son demasiados, por
eso para facilitar el proceso, utilizamos un ciclo Para y
así mostrar todos los datos con un sólo mensaje.

13. 13

14. 14

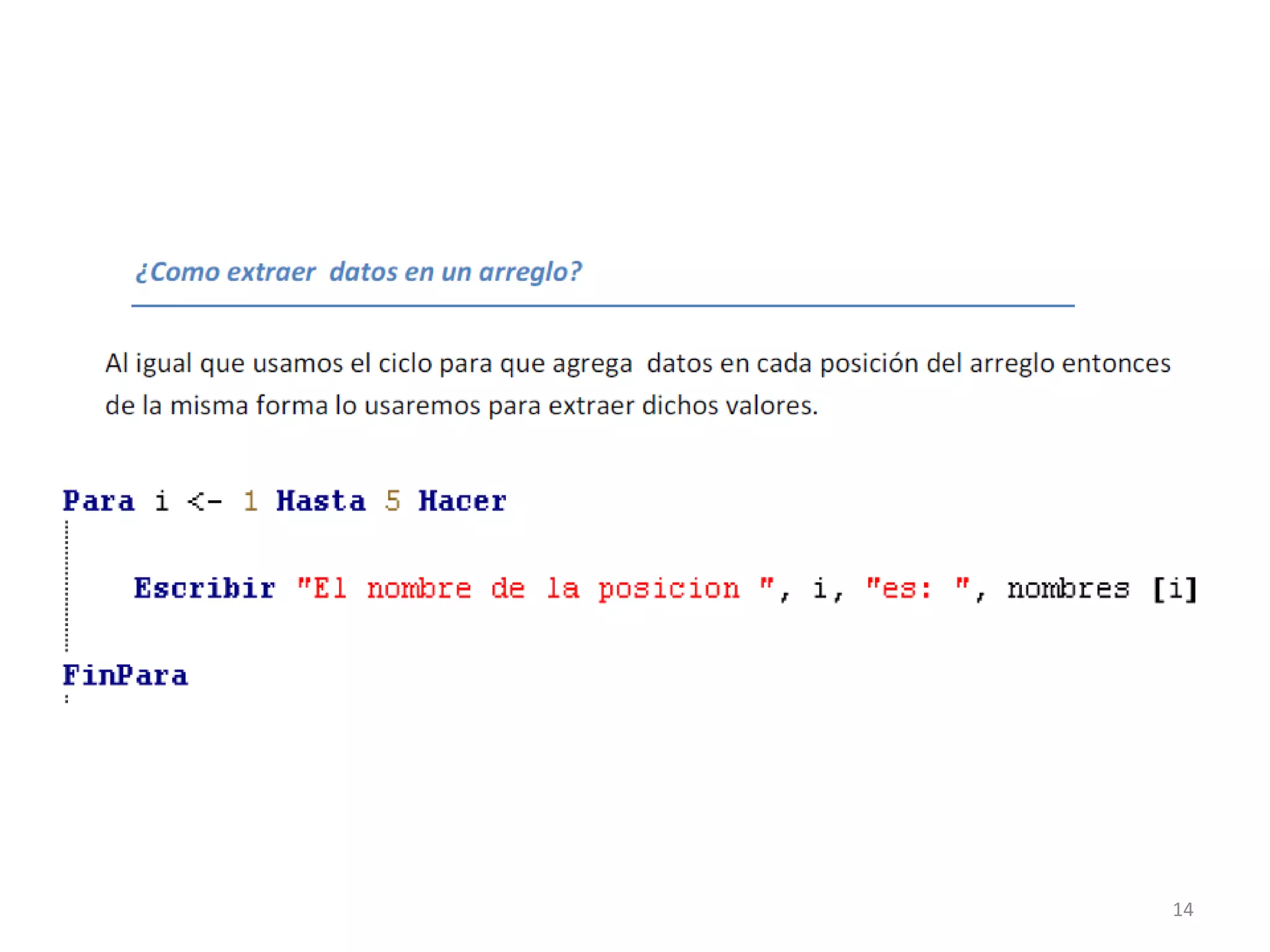
15. 15
Ejemplo 1aAlgoritmo vector1
Inicio
Definir num,i Como Entero
Dimension num[7];
i<-0;
num[0]<-20;
num[1]<-14;
num[2]<-8;
num[3]<-0;
num[4]<-5;
num[5]<-19;
num[6]<-24;
Para i<-1 Hasta 6 Con Paso 1 Hacer
Escribir "El dato en la posición 0 es: ",num[i];
FinPara
Fin

16. Ejemplo 1c
//Crear un arreglo llamado num que almacene los siguientes datos: 20, 14, 8, 0, 5, 19 y 24
Proceso vector1
Definir num,i,numero Como Entero
//Creamos el arreglo, le damos nombre y tamaño de 7 posiciones
Dimension num[7];
//A cada posición le damos un dato, empieza en cero por lo tanto es 0 a 6
Para i<-0 Hasta 6 Con Paso 1 Hacer
Escribir "Ingresa un numero para la posición ",i;
Leer numero;
num[i]<-numero
FinPara
//Imprimimos los datos asignados con un ciclo PARA
Para i<-0 Hasta 6 Con Paso 1 Hacer
Escribir "El dato en la posición ",i," es: ",num[i];
FinPara
FinProceso
16

17. Ejemplo 2
• Crear un arreglo de n posiciones y llenarlo con
nombres de personas.
17

18. Algoritmo vector2
Inicio
Definir n,i Como Entero
Definir nombre,persona Como caracter;
Escribir "Ingrese el numero de posiciones";
Leer n;
Dimension persona[n];
Para i<-0 Hasta n-1 Con Paso 1 Hacer
Escribir "Ingresa el nombre de la persona para la posición ",i;
Leer nombre;
persona[i]<-nombre
FinPara
Para i<-0 Hasta n-1 Con Paso 1 Hacer
Escribir "El nombre en la posición ",i," es: ",persona[i];
FinPara
Fin
18

19. 19

20. Ejemplo 4
• Crear dos arreglos uno que almacene 2
nombres y otro que almacene 3 números.
20

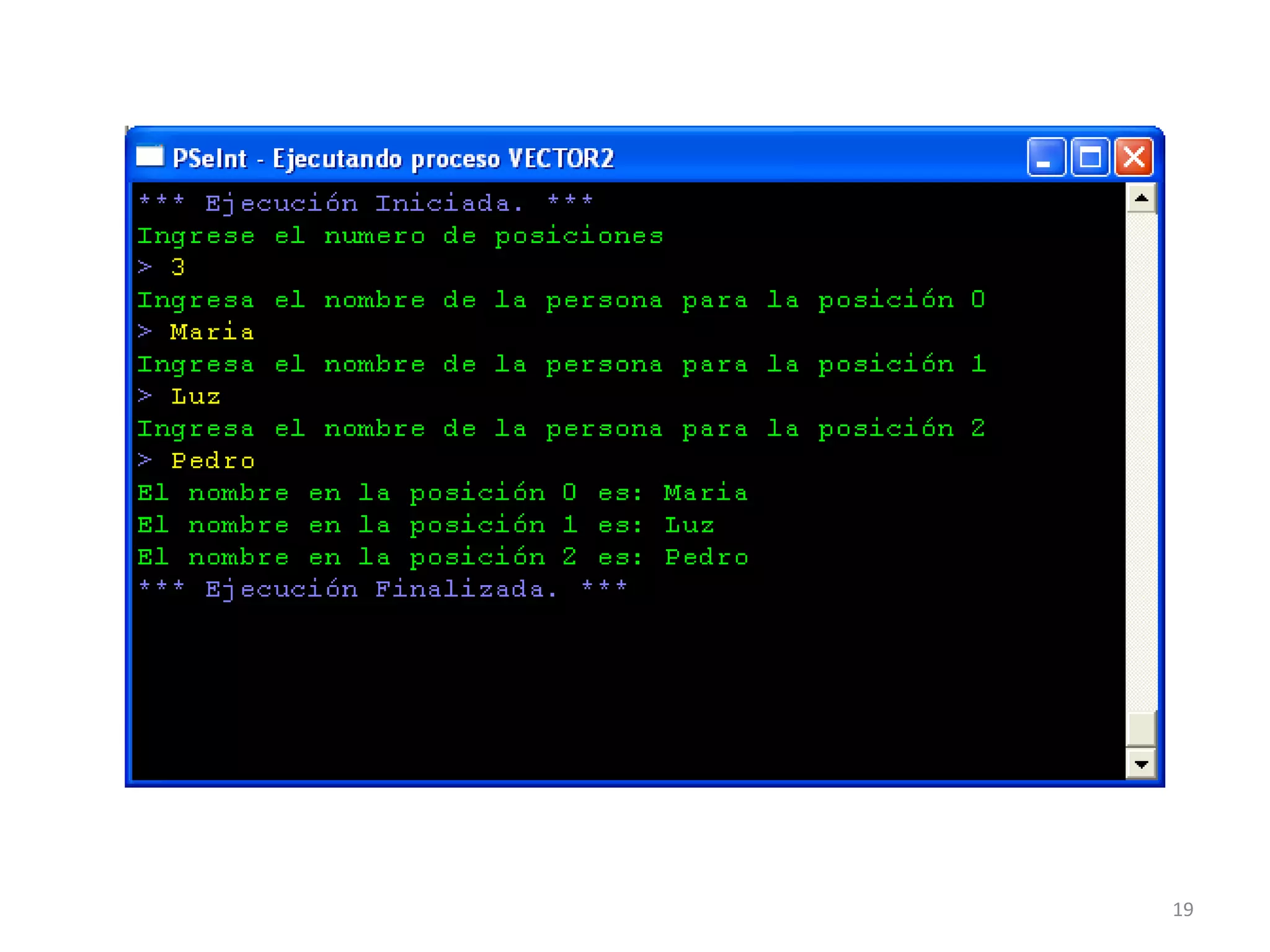
21. Algortimo vector3
Inicio
Definir n,i,num Como Entero
Definir nombre,persona Como caracter;
Dimension persona[2], num[3];
Escribir "Arreglo 1";
Para i<-0 Hasta 1 Con Paso 1 Hacer
Escribir "Ingresa el nombre de la persona para la posición ",i;
Leer nombre;
persona[i]<-nombre
FinPara
Escribir "Arreglo 2";
Para i<-0 Hasta 2 Con Paso 1 Hacer
Escribir "Ingresa el numero para la posición ",i;
Leer n;
num[i]<-n
FinPara
Para i<-0 Hasta 1 Con Paso 1 Hacer
Escribir "El nombre en la posición ",i," es: ",persona[i];
FinPara
Para i<-0 Hasta 2 Con Paso 1 Hacer
Escribir "El numero en la posición ",i," es: ",num[i];
FinPara
Fin
21

22. 22

23. Ejemplo 5
• Sumar todos los elementos de un arreglo de
tamaño n.
23

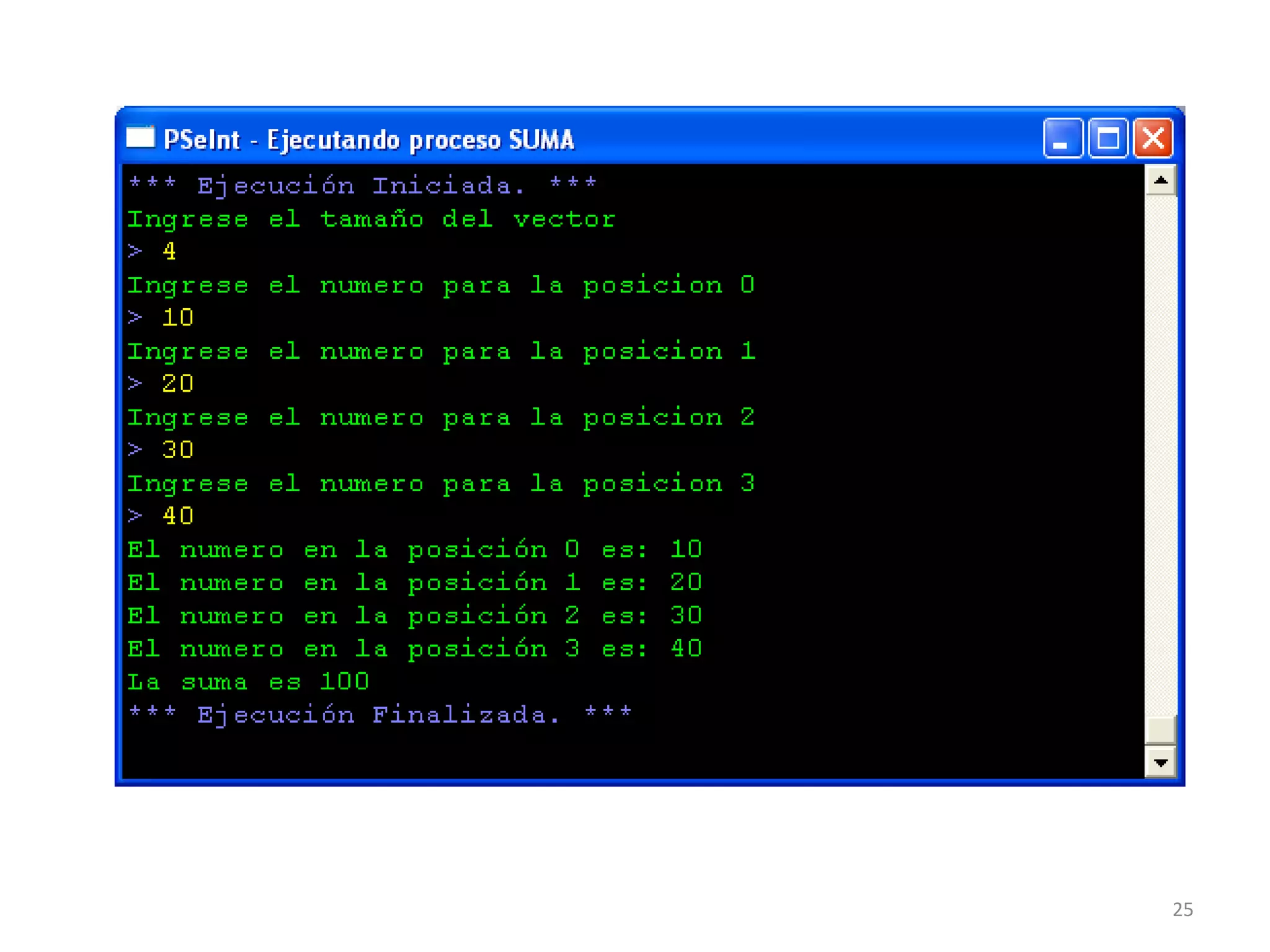
24. Algoritmo suma
Inicio
Definir i,acum,n,num,t Como Entero
acum<-0;
Escribir "Ingrese el tamaño del vector";
Leer t;
Dimension num[t];
Para i<-0 Hasta t-1 Con Paso 1 Hacer
Escribir "Ingrese el numero para la posicion ",i;
Leer n;
num[i]<-n;
acum<-acum+n;
FinPara
Para i<-0 Hasta t-1 Con Paso 1 Hacer
Escribir "El numero en la posición ",i," es: ",num[i];
FinPara
Escribir "La suma es ", acum;
Fin
24

25. 25

26. Ejemplo 6
• Sumar los elementos de dos vectores y
guardar el resultado en otro vector.
26

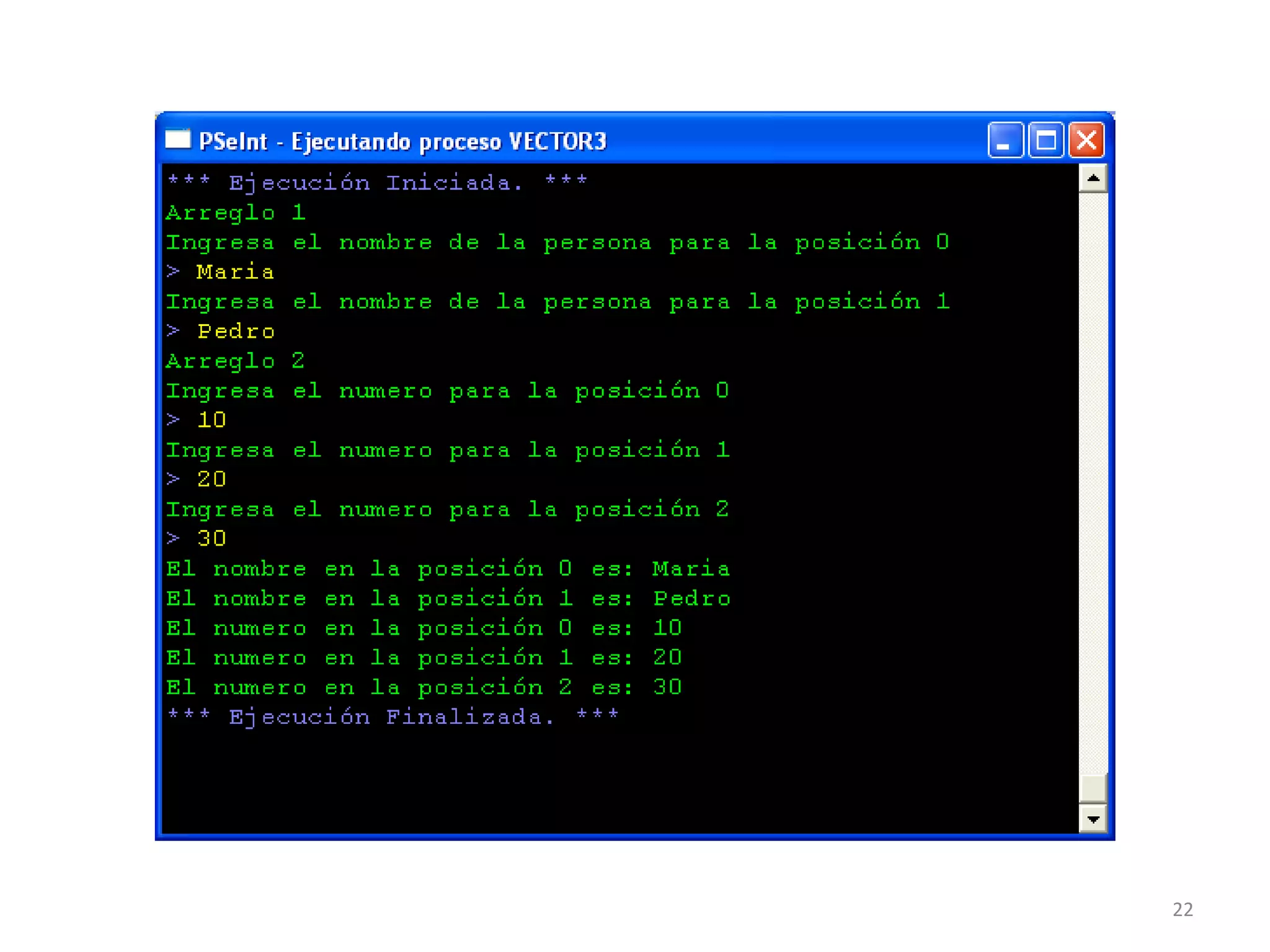
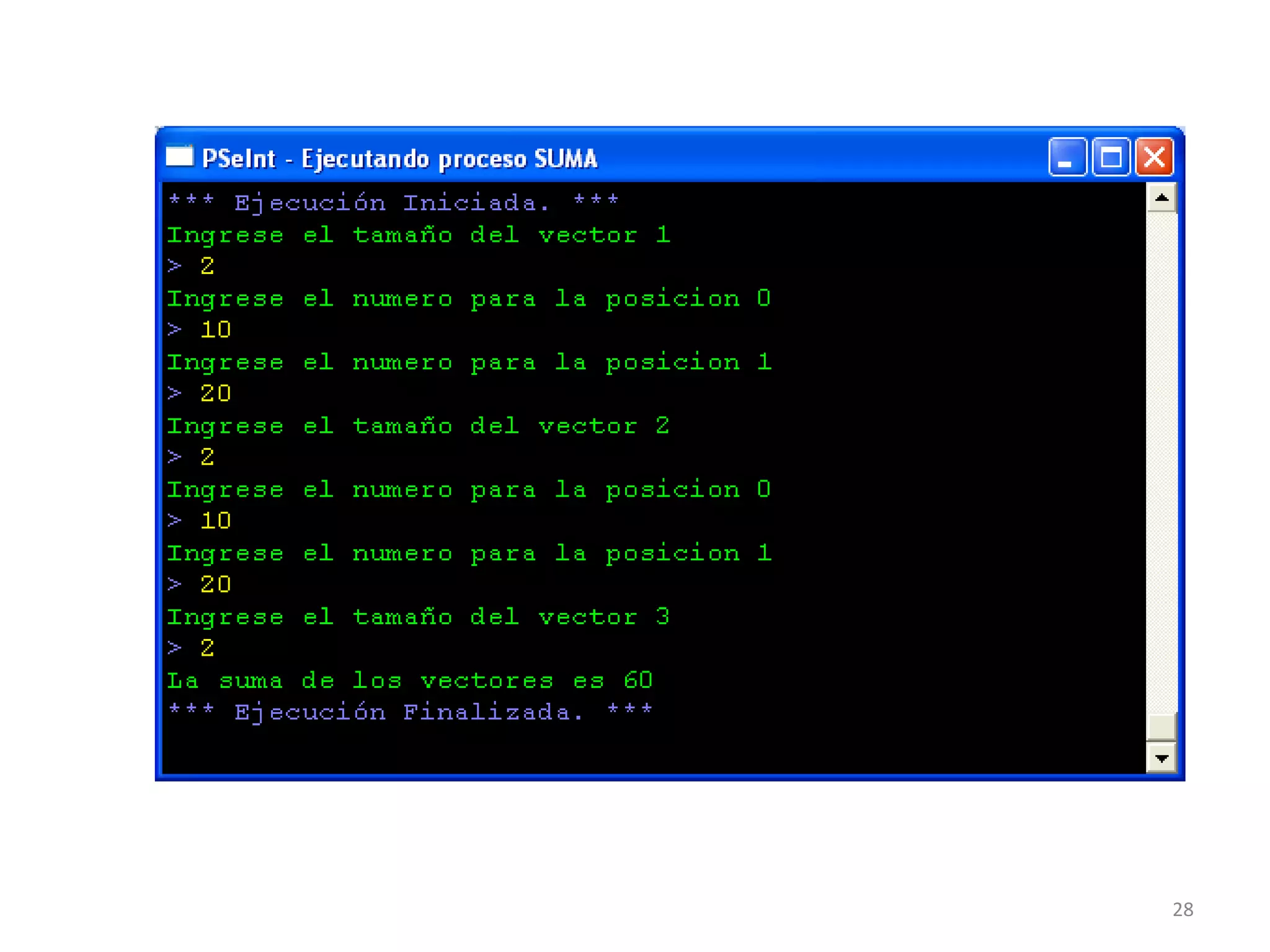
27. Algoritmo suma
Definir i,acum,acum2,n,vector1,vector2,t Como Entero
acum<-0;
acum2<-0;
Escribir "Ingrese el tamaño del vector 1";
Leer t;
Dimension vector1[t];
Para i<-0 Hasta t-1 Con Paso 1 Hacer
Escribir "Ingrese el numero para la posicion ",i;
Leer n;
vector1[i]<-n;
acum<-acum+n;
FinPara
Escribir "Ingrese el tamaño del vector 2";
Leer t;
Dimension vector2[t];
Para i<-0 Hasta t-1 Con Paso 1 Hacer
Escribir "Ingrese el numero para la posicion ",i;
Leer n;
vector2[i]<-n;
acum2<-acum2+n;
FinPara
Escribir "Ingrese el tamaño del vector 3";
Leer t;
Dimension vector3[t];
vector3[1]<-acum+acum2;
Escribir "La suma de los vectores es ",vector3[1];
Fin
27

28. 28

29. Ejemplo 7
• Crear una matriz 2x2 que almacene los
siguientes valores: 10, 20, 30, 40.
29

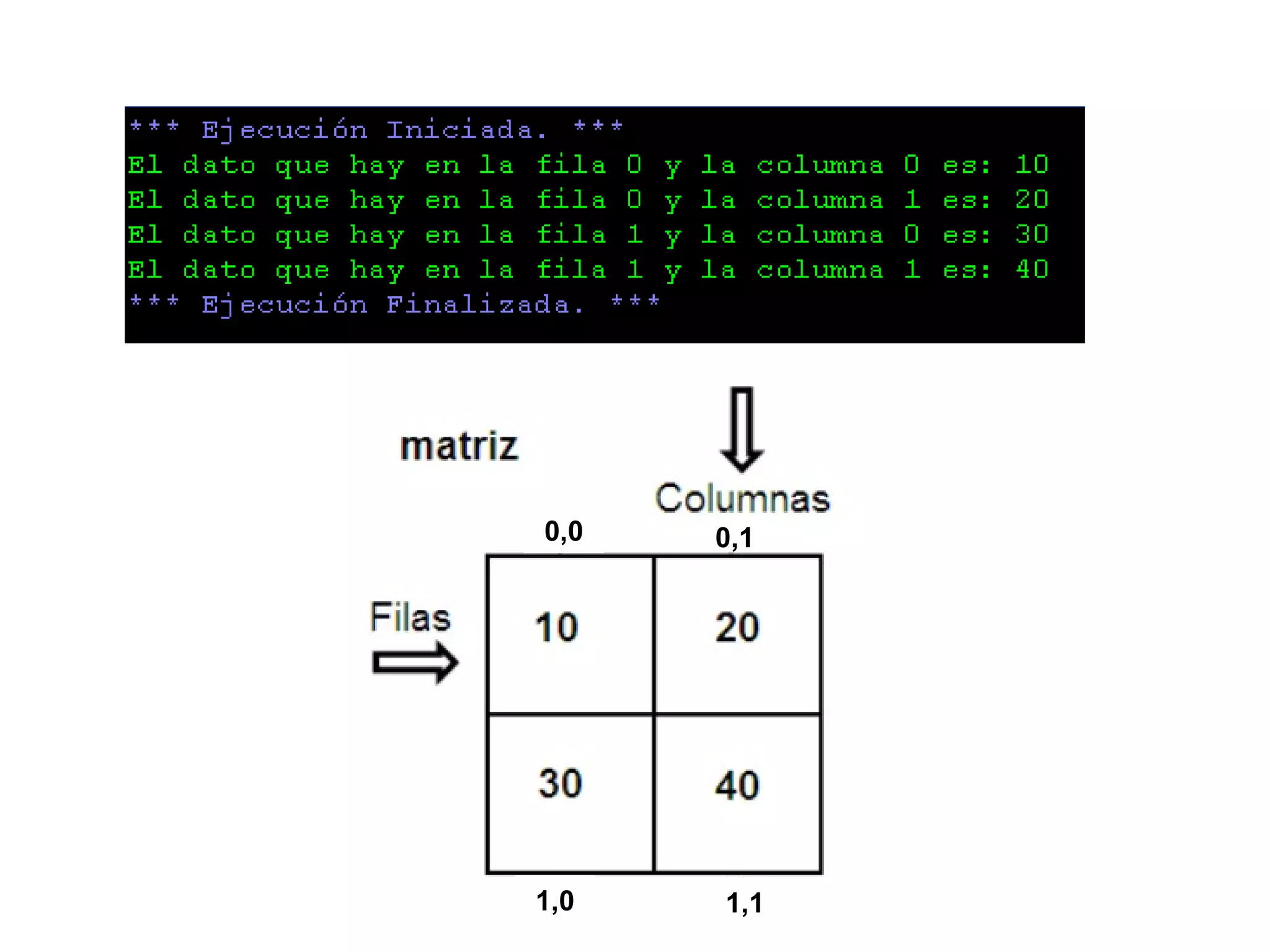
30. Algoritmo matriz1
Inicio
Definir matriz como entero;
Dimension matriz[2,2];
matriz[0,0]<-10;
matriz[0,1]<-20;
matriz[1,0]<-30;
matriz[1,1]<-40;
Escribir "El dato que hay en la fila 0 y la columna 0 es: ",matriz[0,0];
Escribir "El dato que hay en la fila 0 y la columna 1 es: ",matriz[0,1];
Escribir "El dato que hay en la fila 1 y la columna 0 es: ",matriz[1,0];
Escribir "El dato que hay en la fila 1 y la columna 1 es: ",matriz[1,1];
Fin
30

31. 0,0 0,1
1,11,0

32. Ejemplo 8
• Crear una matriz de n filas y n columnas. Llenar la
matriz con los números que el usuario desee.
32

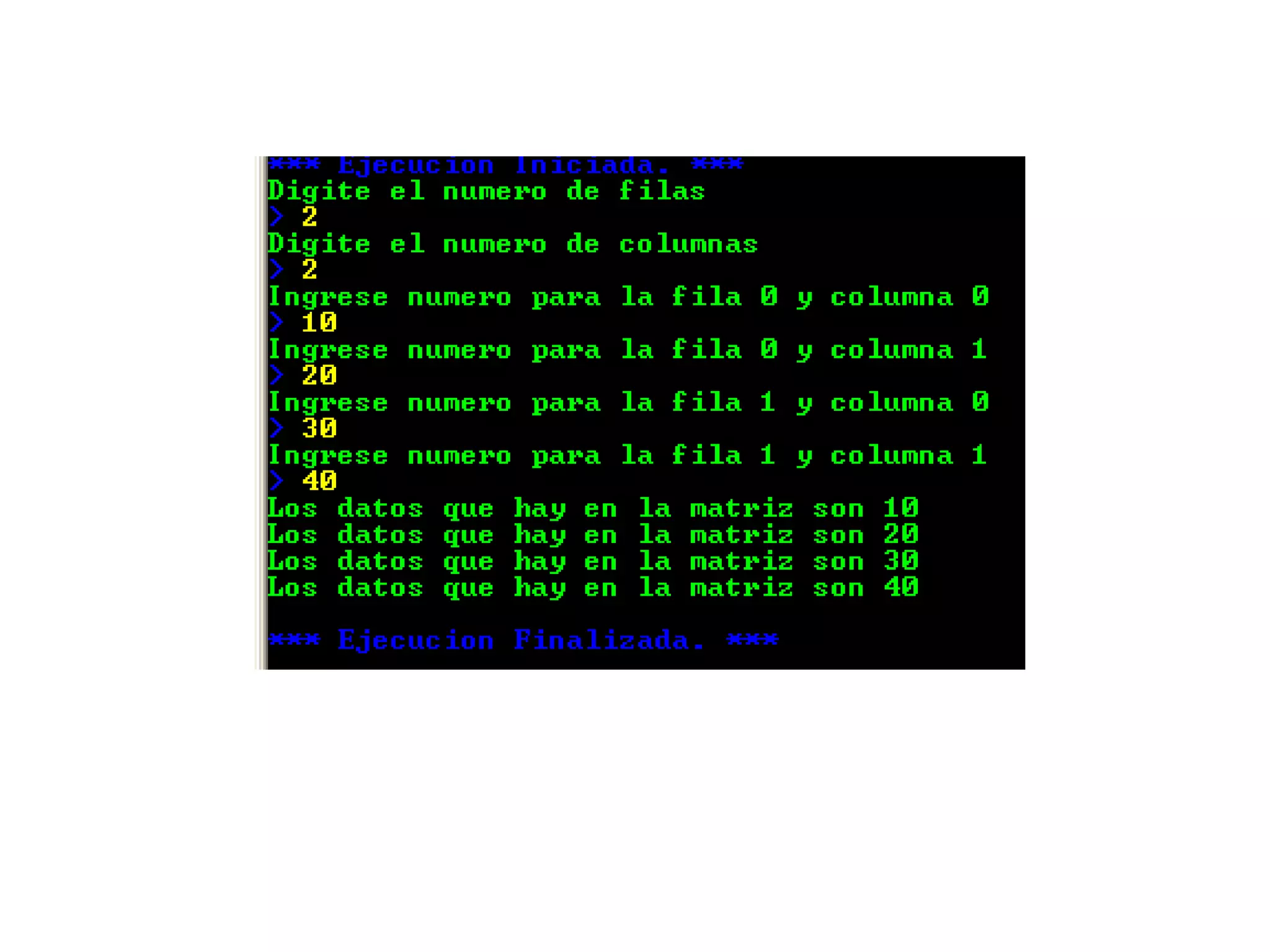
33. Algoritmo matriz2
Inicio
Definir matriz,f,c,i,j como entero;
//Pedimos el numero de filas
Escribir "Digite el numero de filas";
Leer f;
//Pedimos el numero de columnas
Escribir "Digite el numero de columnas";
Leer c;
//Creamos la matriz
Dimension matriz[f,c];
//Llenamos la matriz con 2 ciclos PARA, uno para filas y otro para columnas
Para i<-0 Hasta f-1 Con Paso 1 Hacer
Para j<-0 Hasta c-1 Con Paso 1 Hacer
//Pedimos los datos
Escribir "Ingrese numero para la fila ",i," y columna ",j;
Leer numero;
//Llenamos la matriz con los numeros ingresados
matriz[i,j]<-numero;
FinPara
FinPara
//Mostramos todos los datos que en la matriz
Para i<-0 Hasta f-1 Con Paso 1 Hacer
Para j<-0 Hasta c-1 Con Paso 1 Hacer
Escribir "Los datos que hay en la matriz son ",matriz[i,j];
FinPara
FinPara
Fin
33

35. Ejemplo 9
• Crear una matriz n x n y llenarla con los
números que el usuario desee.
• Sume todos los números que componga la
columna 1.
35

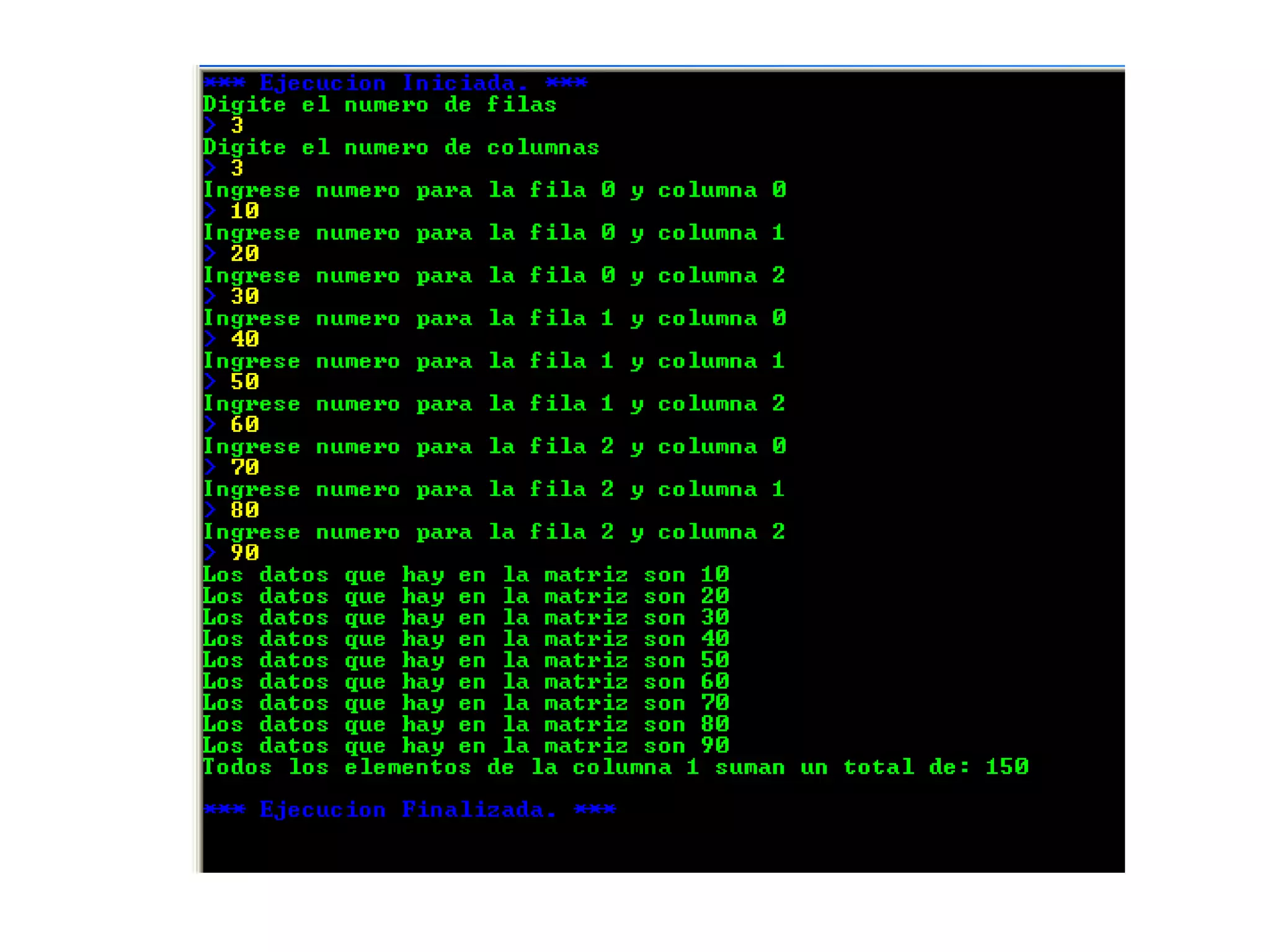
36. Algoritmo matriz2
Inicio
Definir matriz,f,c,i,j,acum como entero;
//Inicializamos acum en cero
acum<-0;
//Pedimos el numero de filas
Escribir "Digite el numero de filas";
Leer f;
//Pedimos el numero de columnas
Escribir "Digite el numero de columnas";
Leer c;
//Creamos la matriz
Dimension matriz[f,c];
//Llenamos la matriz con 2 ciclos PARA, uno para filas y otro para columnas
Para i<-0 Hasta f-1 Con Paso 1 Hacer
Para j<-0 Hasta c-1 Con Paso 1 Hacer
//Pedimos los datos
Escribir "Ingrese numero para la fila ",i," y columna ",j;
Leer numero;
//Llenamos la matriz con los numeros ingresados
matriz[i,j]<-numero;
FinPara
//Sumamos todos los números de la columna 1
acum<-acum+matriz[i,1];
FinPara
//Mostramos todos los datos que en la matriz
Para i<-0 Hasta f-1 Con Paso 1 Hacer
Para j<-0 Hasta c-1 Con Paso 1 Hacer
Escribir "Los datos que hay en la matriz son ",matriz[i,j];
FinPara
FinPara
//Mostramos la suma de la columna 1
Escribir "Todos los elementos de la columna 1 suman un total de: ",acum;
Fin
36