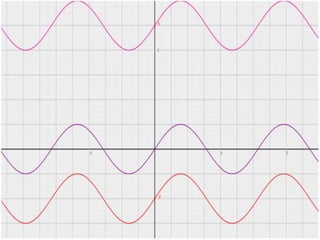
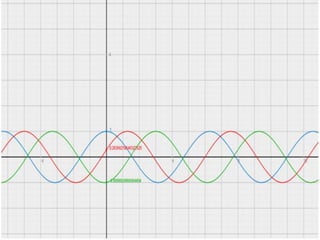
La gráfica de una función puede trasladarse vertical u horizontalmente. Una traslación vertical implica sumar un número real a la función, mientras que una traslación horizontal implica sumar un número real al ángulo de la función. Esto se ilustra con ejemplos de traslaciones verticales y horizontales de las funciones seno y coseno.

1. Omar Sebastián Contreras Poveda

2. Sea f(x) una función, la grafica de dicha
función se puede trasladar vertical y
horizontalmente.
Traslación vertical : sea la función
f(x) =(x), la grafica de tal función se puede
trasladar de manera vertical sumando a la
función cualquier numero real como en el
siguiente ejemplo:

4. Donde tales graficas corresponden a :
f(x) = sen(x)
f(x) = sen(x) + 5
f (x) = sen(x) – 2
Traslación horizontal: sea la función
f(x) = sen(x), la grafica de tal función se puede
trasladar de manera horizontal sumando al
Angulo de la función cualquier numero real
como en el siguiente ejemplo:

6. Donde tales graficas corresponden a :
f(x) = cos(x)
f(x) = cos(x) + 3
f (x) = cos(x) – 5