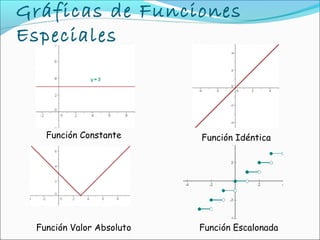
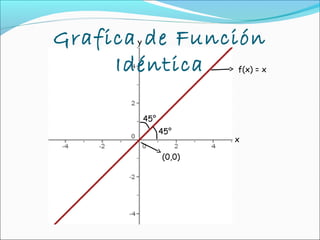
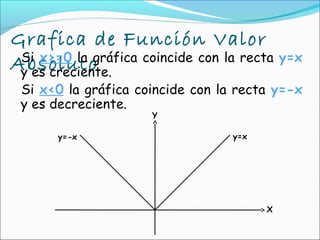
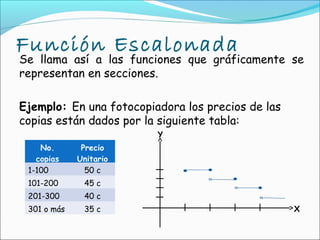
Este documento describe cuatro tipos de funciones especiales: función constante, función idéntica, función valor absoluto y función escalonada. Explica sus características gráficas y matemáticas, así como ejemplos de cada una. Incluye actividades para reforzar el entendimiento de estas funciones.

1. Elaborado por:
I.S.C. Anabel Cárdenas

2. Funciones Especiales
Existen cuatro tipos de funciones que pueden
calificarse como especiales.
 Función constante
 Función idéntica
 Función valor absoluto
 Función escalonada

3. Gráficas de Funciones
Especiales
Función Constante Función Idéntica
Función Valor Absoluto Función Escalonada

4. Función Constante
Es una ecuación de la forma f(x)=k, donde k es una
constante.
Ejemplo: f(x) = 4
Gráficamente esta función es una línea horizontal
paralela al eje x que pasa por el punto (0,k).

5. Ejemplo: f(x)=9.8 m/s² donde 9.8 es la constante
de la aceleración, sin importar desde que distancia
se arroje un cuerpo siempre está influido por esta
constante.
y
El dominio de una
k = 9.8
función constante
es R.
El rango es {k}.
x

6. Actividad
Contesta las siguientes preguntas:
1.-¿A qué es igual una función constante?
2.-¿A qué eje es paralela la gráfica de una función
constante?
3.-¿Por qué punto pasa?

7. Función Idéntica = x.
Es la función cuya ecuación es f(x)
Su grafica es una recta que pasa por el punto (0,0) y
esta a 45° del eje X y del eje Y.
Se llama función identidad porque Y es igual a X
siempre.
El dominio y el rango de la función idéntica es R.

8. Grafica de Función
y
Idéntica f(x) = x
45°
45°
x
(0,0)

9. Actividad
Escribe con tus propias palabras que es una función
idéntica y cuales son sus características.

10. Función Valor Absoluto
El valor absoluto se escribe así:
x si x>=0
|x| =
x si x<0
El dominio de la función valor absoluto es R y el
rango es R+.
La función valor absoluto se escribe f(x)= |x|

11. Grafica de Función Valor
Si x>=0 la gráfica coincide con la recta y=x
Absoluto
y es creciente.
Si x<0 la gráfica coincide con la recta y=-x
y es decreciente.
Y
y=-x y=x
X

12. Actividad
Relaciona las columnas.
Dominio de función constante.
Dominio de función idéntica. R+
Dominio de función valor absoluto. {k}
Rango de función constante. R
Rango de función idéntica.
Rango de función valor absoluto.

13. Función Escalonada
Se llama así a las funciones que gráficamente se
representan en secciones.
Ejemplo: En una fotocopiadora los precios de las
copias están dados por la siguiente tabla:
Y
No. Precio
copias Unitario
1-100 50 c
101-200 45 c
201-300 40 c
301 o más 35 c X

14. Actividad
Contesta las siguientes preguntas.
¿Cuál es el dominio de esta función?
¿Cuál es el rango de esta función?
¿Qué representan en la gráfica los círculos vacíos?
¿Qué representan en la gráfica los círculos llenos?
Escribe 3 ejemplos de funciones escalonadas que
encuentras en la vida cotidiana.
La notación para esta función es:
50 si 0 < x <= 100
45 si 100 < x <= 200
40 si 200 < x <= 300
35 si x > 300