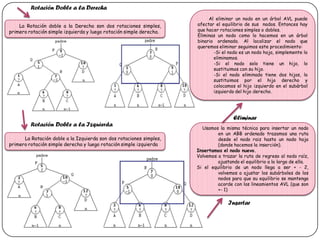
Este documento describe las técnicas de rotación en árboles balanceados como los árboles AVL. Explica las rotaciones simples y dobles a la izquierda y derecha que mantienen el equilibrio del árbol cuando se insertan o eliminan nodos. También define los árboles AVL como árboles binarios donde todos los nodos del subárbol izquierdo son menores que la raíz y todos los del derecho son mayores.

1. República Bolivariana de Venezuela
Decanato de Ingeniería
Universidad Fermín Toro
Cabudare – Edo Lara
MAPA CONCEPTUAL
TECNICAS DE ROTACION EN ARBOLES
BALANCEADOS
Presentado por:
Lourdes Barrios
C.I. 19.954.486
Asignatura: Análisis de Algoritmo
Prof. Ing. Diosmary Marrón
Febrero - 2013

2. Árboles Balanceados
definición
Un grafo se define de la siguiente manera: Un grafo consiste de un
número de nodos (puntos o vértices) y un grupo de arcos que unen parejas de
nodos. A todos los pares de nodos unidos por un arco se les llama nodos
adyacentes. Los arcos pueden tener una dirección determinada, generando así
un grafo dirigido, el cual de lo contrario sería no-dirigido. (También existen los
grafos mixtos). Por convención a los nodos de un grafo sele representa con
círculos y los arcos que los conectan como líneas(no-dirigido) o flechas
(dirigido).
Factor de Equilibrio
Rotación Simple
El factor de equilibrio es la diferencia entre las alturas a la Izquierda:
del árbol derecho y el izquierdo:
FE = altura subárbol derecho - altura subárbol izquierdo; op rotIzq: AVL{X} -> [AVL{X}] .
Por definición, para un árbol AVL, este valor debe ser -1, 0 eq rotIzq(arbolBin(R1, I, arbolBin(R2, I2, D2))) ==
ó1 arbolBin(R2, arbolBin(R1, I, I2), D2) .
Si el factor de equilibrio de un nodo es:
0 -> el nodo está equilibrado y sus subárboles tienen
exactamente la misma altura.
1 -> el nodo está desequilibrado y su subárbol derecho es un
nivel más alto.
-1 -> el nodo está desequilibrado y su subárbol izquierdo es un
nivel más alto.
características:
-Árbol balanceado por altura: en dónde todos
los hijos o nodos hoja se intentan mantener a la Rotación Simple
misma distancia de la raíz. a la Derecha:
-Árbol balanceado por peso: en dónde los
nodos más visitados o utilizados se mantienen a op rotDer: AVL{X} -> [AVL{X}] .
poca distancia dela raíz. eq rotDer(arbolBin(R1, arbolBin(R2, I2, D2), D1)) ==
arbolBin(R2, I2, arbolBin(R1, D2, D)) .
ARBOLES AVL: es un árbol binario en el cual cada nodo cumple con que todos los nodos de su subárbol
izquierdo son menores que la raíz y todos los nodos del subárbol derecho son mayores que la raíz.

3. Rotación Doble a la Derecha
Al eliminar un nodo en un árbol AVL puede
La Rotación doble a la Derecha son dos rotaciones simples, afectar el equilibrio de sus nodos. Entonces hay
primero rotación simple izquierda y luego rotación simple derecha. que hacer rotaciones simples o dobles.
Eliminas un nodo como lo hacemos en un árbol
binario ordenado. Al localizar el nodo que
queremos eliminar seguimos este procedimiento:
-Si el nodo es un nodo hoja, simplemente lo
eliminamos.
-Si el nodo solo tiene un hijo, lo
sustituimos con su hijo.
-Si el nodo eliminado tiene dos hijos, lo
sustituimos por el hijo derecho y
colocamos el hijo izquierdo en el subárbol
izquierdo del hijo derecho.
Eliminar
Rotación Doble a la Izquierda
Usamos la misma técnica para insertar un nodo
en un ABB ordenado trazamos una ruta
La Rotación doble a la Izquierda son dos rotaciones simples, desde el nodo raiz hasta un nodo hoja
primero rotación simple derecha y luego rotación simple izquierda (donde hacemos la inserción).
Insertamos el nodo nuevo.
Volvemos a trazar la ruta de regreso al nodo raíz,
ajustando el equilibrio a lo largo de ella.
Si el equilibrio de un nodo llega a ser + - 2,
volvemos a ajustar los subárboles de los
nodos para que su equilibrio se mantenga
acorde con los lineamientos AVL (que son
+- 1)
Insertar