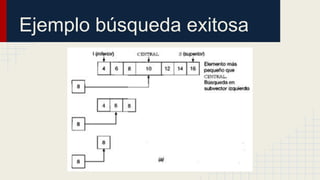
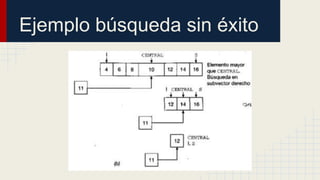
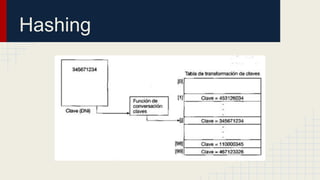
El documento detalla métodos de búsqueda y ordenamiento, incluyendo ejemplos de algoritmos como la búsqueda secuencial, binaria y hashing. Se analizan las ventajas y desventajas de cada método, así como los casos de colisiones en hashing y diferentes técnicas para manejarlas. Incluye ejercicios prácticos para aplicar ordenamientos a listas numéricas y utiliza tablas intermedias para mostrar el proceso.

1. Búsquedas
Unidad 4
ING. ALVARO ENRIQUE RUANO

2. Ejercicio Ordenamientos
Para el siguiente listado de arreglos, aplicar todos los métodos de
ordenamiento (ascendente) vistos en clase. Se deberán presentar todas las
tablas intermedias realizadas durante el proceso así como el listado de
intercambios realizados:
• 45,65,23,46,78,11,23,21,20,0
• 7,6,5,4,3,2,1

3. Contenido
● Búsqueda
● Métodos de Búsqueda
o Secuencial
o Binaria
o Hashing

4. Búsqueda
● La búsqueda es una de las aplicaciones más importantes de las
computadoras.
● También es conocida como recuperación o searching.
● Es una operación para encontrar la posición de un elemento entre un
conjunto de elementos dados: lista, tabla o archivo.

5. Búsqueda
● Las búsquedas pueden clasificarse según el medio de almacenamiento
donde se encuentran los registros:
o Búsqueda interna: Es aquella que se realiza completamente en la
memoria RAM
o Búsqueda externa: Es aquella que se realiza dentro de archivos en
almacenamiento secundario (disco duro, memoria flash, cinta, etc.).

6. Búsqueda
● Existen diversos algoritmos de búsqueda, pero la elección dependerá de
la forma en que se encuentran almacenados los datos.
● Por definición, se considera a un algoritmo como “algoritmo de búsqueda”
si cumple las siguientes dos condiciones:
o Puede determinar si X pertenece al conjunto e indicar su posición
o Puede determinar si X no pertenece al conjunto

7. Búsqueda
● Existen diversos algoritmos de búsqueda, pero la elección dependerá de
la forma en que se encuentran almacenados los datos.
o Secuencial
o Binario
o Por transformación de claves hash.
● Por definición, se considera a un algoritmo como “algoritmo de búsqueda”
si cumple las siguientes dos condiciones:
o Puede determinar si X pertenece al conjunto e indicar su posición
o Puede determinar si X no pertenece al conjunto

8. Búsqueda Secuencial
● Es la forma más sencilla de búsqueda.
● Se dice que es una exploración secuencial del listado, de ahí viene el
nombre del método.
● Consiste en comparar cada elemento del listado contra el valor deseado.
● Tiene dos condiciones de finalización
o Cuando se encuentra el valor
o Cuando se termina de leer por completo el listado

9. Búsqueda Secuencial
● Ventajas
o Es sencillo de implementar ya que únicamente se utilizan estructuras
repetitivas.
o No requiere que el listado esté ordenado o en algún estado especial.
● Desventajas
o El poco eficiente ya que se debe recorrer por completo el arreglo.
o Tiempo excesivo de procesamiento en vectores grandes.
o Se requerirán (N+1)/2 comparaciones en promedio.
o En el peor de lo casos se requieren N comparaciones.

10. Algoritmo 1

11. Mejoras al Algoritmo 1
● El algoritmo 1 realiza dos comparaciones en cada iteración:
o Una para comparar si se encuentra el elemento t
o La otra para evaluar si ya se llegó al final del vector
● Se puede mejorar el rendimiento disminuyendo a una comparación por
iteración al agregar un “valor centinela” que permita descubrir si ya se
terminó de recorrer el vector.
● Se utiliza el valor buscado como valor centinela y se coloca al final del
arreglo (en una posición adicional) para forzar a que el algoritmo siempre
tenga éxito encontrando el valor buscado.

12. Algoritmo 2

13. Búsqueda Binaria
● Es eficiente cuando tratamos con conjuntos grandes de datos.
● Requiere que los datos estén ordenados.
● Se basa en la división sucesiva del espacio ocupado por el arreglo en
sucesivas mitades.
● Se basa en la estrategia de “divide y vencerás”

14. Búsqueda Binaria
o Se examina el elemento central de la lista.
o Si es el elemento buscado, se termina la búsqueda.
o Si no es el elemento buscado, se determina si el elemento buscado es
mayor o menor al central. Esto nos indicará si este elemento se encuentra
en la primera mitad de la lista o en la segunda mitad.
o Se elige la nueva mitad a evaluar y se repite este proceso utilizando el
elemento central de cada sublista.

15. Ejemplo búsqueda exitosa

16. Ejemplo búsqueda sin éxito

17. Algoritmo

18. Búsqueda Binaria
● Cantidad de comparaciones en el peor caso:
● Cantidad de comparaciones en el caso promedio

19. Comparación

20. Hashing
● También llamado búsqueda mediante transformación de claves.
● No se requiere que los datos estén ordenados.
● Consiste en convertir una clave dada (valor de búsqueda) en una
dirección dentro del listado donde se almacenan los valores (al momento
del almacenamiento).
● Esta misma conversión se realizará al momento de realizar la búsqueda,
obteniendo de forma inmediata la posición dentro del listado.

21. Hashing
● Existen casos donde es sencillo encontrar una función de conversión.
o Por ejemplo una lista de 100 empleados, donde el código de
empleado es un número del 1 al 100, la correspondencia es directa.
● Existen otros casos donde no es posible establecer una relación como el
inciso anterior.
o Por ejemplo, si necesitamos que el campo de búsqueda sea el
número de documento de identificación (varios millones) para una
muestra de 100 empleados.

22. Hashing

23. Hashing
● La conversión entre las claves y la posición en el listado es realizada por
una función denominada “función de conversión” o “función hash”.
● Se dice que el objetivo de la función H(k) es convertir una clave k en una
dirección d.
● En el ejemplo anterior, la función H(k) convierte valores en un rango de
varios millones (número de documento de identificación) a un rango de
100 valores (tamaño del arreglo o lista).

24. Colisiones
● Existen casos donde para dos valores k de entrada, se producirá la misma
salida d, estos casos se llaman “Colisiones”.
● La colisión se soluciona definiendo la forma en que se se encuentra un
valor alternativo (d1, d2, …, dn) para almacenar el registro en esta nueva
posición.
● El éxito de esta técnica está en dos factores:
o La elección de la función H
o El procedimiento para manejo de colisiones

25. Colisiones
Solución de colisiones utilizando listas.

26. Métodos de Hashing
Truncamiento:
● Ignora una parte de la clave y se utiliza la parte restante directamente
como índice.
● Es un método muy rápido pero falla para distribuir las claves de forma
uniforme.
Ejemplo:
● Entrada: 7490312
● Proceso: Se trunca 90312
● Salida: 74

27. Métodos de Hashing
Plegamiento:
● Se divide la clave en diferentes partes.
● Las distintas partes se combinan de un modo conveniente, a menudo
suma o multiplicación
● Es recomendable que las partes tengan la misma cantidad de dígitos que
se espera tenga la salida.
● Se truncan los dígitos “sobrantes” más significativos de la salida.
Ejemplo:
● Entrada: 7490312
● Proceso: 74 + 90 + 31 + 2 = 197, se trunca a 97
● Salida: 97

28. Métodos de Hashing
Aritmética Modular:
● Se utiliza la función MOD para dividir la entrada dentro del rango del
índice (tamaño del array o lista).
● Se mejora la efectividad utilizando número primos cercanos al rango.
Ejemplo:
● Entrada: 7490312
● Proceso:
o Tamaño 100, el menor primo es 97.
o 7490312 MOD 97 = 69
● Salida: 69

29. Métodos de Hashing
Mitad del cuadrado:
● Se calcula el cuadrado de la clave y luego se seleccionan números de la
parte intermedia.
● Siempre se deben seleccionar las mismas posiciones dentro del cuadrado.
Ejemplo:
● Entrada: 7490312
● Proceso:
o 7490312^2 = 56,104,773,857,344
o Se toman las posiciones 6 y 7.
● Salida: 77

30. Asistencia
● Toma de asistencia.

31. Gracias por su atención