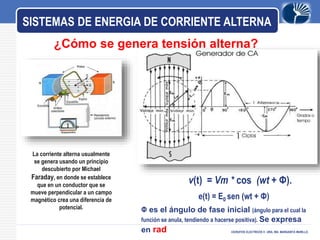
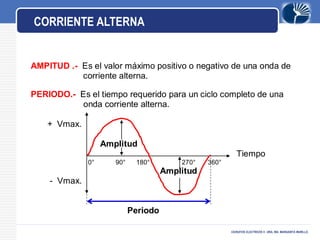
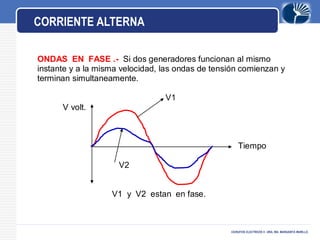
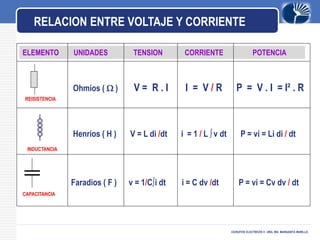
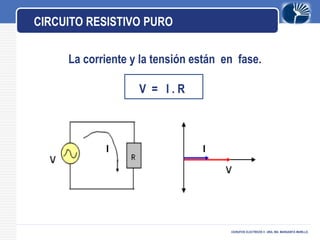
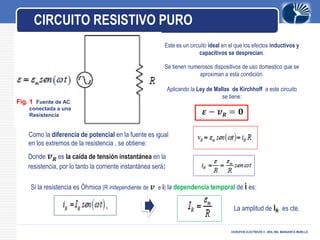
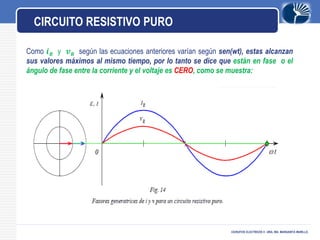
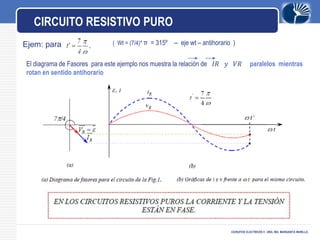
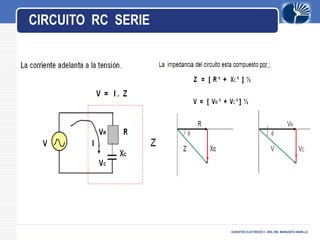
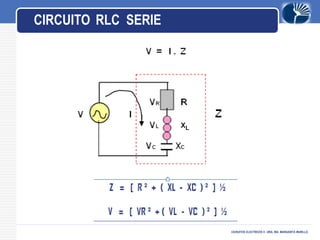
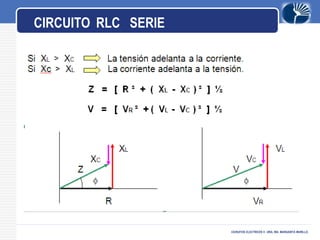
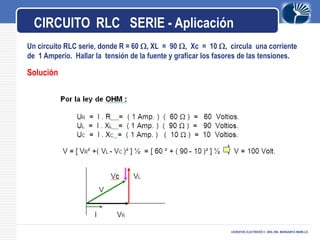
Este documento presenta información sobre circuitos eléctricos de corriente alterna. Explica cómo se genera la tensión alterna usando el principio descubierto por Faraday. Luego describe conceptos clave como frecuencia, amplitud, período, ondas en fase y desfasadas. También analiza circuitos resistivos puros, capacitivos puros e inductivos puros, y explica la relación entre voltaje y corriente en cada uno. Por último, cubre circuitos RLC en serie y resonancia.

1. LOGO
S2- Análisis de Circuitos Eléctricos II
Dra. ING. MARGARITA MURILLO MANRIQUE - e-mail: mmurillo@uch.edu.pe
ESCUELA DE INGENIERÍA ELECTRÓNICA
CON MENCION EN
TELECOMUNICACIONES
CIRCUTOS Nilson PAG. 400-

2. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
SISTEMAS DE ENERGIA DE CORRIENTE ALTERNA
¿Cómo se genera tensión alterna?
La corriente alterna usualmente
se genera usando un principio
descubierto por Michael
Faraday, en donde se establece
que en un conductor que se
mueve perpendicular a un campo
magnético crea una diferencia de
potencial.
v(t) = Vm * cos (wt + Ф).
e(t) = E0 sen (wt + Ф)
Ф es el ángulo de fase inicial (ángulo para el cual la
función se anula, tendiendo a hacerse positiva). Se expresa
en rad

3. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CORRIENTE ALTERNA
¿QUE ES LA FRECUENCIA EN UNA ONDA ALTERNA ?
Es el número de ciclos generados cada segundo.
Volt. 1 ciclo 1 ciclo 1 ciclo
Tiempo
1 segundo
F = 3 ciclos / 1 segundo = 3 ciclos/segundo = 3 hertz = 3 Hz.

4. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
AMPITUD .- Es el valor máximo positivo o negativo de una onda de
corriente alterna.
PERIODO.- Es el tiempo requerido para un ciclo completo de una
onda corriente alterna.
+ Vmax.
Amplitud
Tiempo
0° 90° 180° 270° 360°
Amplitud
- Vmax.
Periodo
CORRIENTE ALTERNA

5. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CORRIENTE ALTERNA
RELACION ENTRE PERIODO Y FRECUENCIA
Periodo = 1 / Frecuencia ( F )
T Segundos ( Seg. )
F Ciclos / seg. ( Hz )
Ejemplo.- Si T = 1 mseg. ó T = 0.001 Seg.
F = 1 / T = 1 / 0.001
F = 1000 Hz. ó F = 1 KHz.

6. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CORRIENTE ALTERNA
ONDAS EN FASE .- Si dos generadores funcionan al mismo
instante y a la misma velocidad, las ondas de tensión comienzan y
terminan simultaneamente.
V1
V volt.
Tiempo
V2
V1 y V2 estan en fase.

7. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CORRIENTE ALTERNA
ONDAS DESFASADAS.- Si un generador arranca después de
otro sus valores máximos y mínimos ocurriran despues de los
valores correspondiente al otro generador.
V1
V volt.
V2
Tiempo
V1 esta adelantada en 90° respecto de V2.
V2 esta retrazado en 90° respecto de V1.

8. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
RELACION ENTRE VOLTAJE Y CORRIENTE
ELEMENTO UNIDADES TENSION CORRIENTE POTENCIA
Ohmios (  ) V = R . I I = V / R P = V . I = I² . R
Henrios ( H ) V = L di /dt i = 1 / L ∫v dt P = vi = Li di / dt
Faradios ( F ) v = 1/C∫i dt i = C dv /dt P = vi = Cv dv / dt
REISISTENCIA
INDUCTANCIA
CAPACITANCIA

9. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RESISTIVO PURO
La corriente y la tensión están en fase.
V = I . R

10. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RESISTIVO PURO
Este es un circuito ideal en el que los efectos inductivos y
capacitivos se desprecian.
Se tienen numerosos dispositivos de uso domestico que se
aproximan a esta condición.
Aplicando la Ley de Mallas de Kirchhoff a este circuito
se tiene:
𝜺 − 𝒗 𝑹 = 𝟎
Como la diferencia de potencial en la fuente es igual
en los extremos de la resistencia , se obtiene:
Donde 𝒗 𝑹 es la caída de tensión instantánea en la
resistencia, por lo tanto la corriente instantánea será:
Si la resistencia es Óhmica (R independiente de 𝒗 e i) la dependencia temporal de i es:
La amplitud de IR es cte.
Fig. 1 Fuente de AC
conectada a una
Resistencia

11. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RESISTIVO PURO
Como 𝒊 𝑹 y 𝒗 𝑹 según las ecuaciones anteriores varían según sen(wt), estas alcanzan
sus valores máximos al mismo tiempo, por lo tanto se dice que están en fase o el
ángulo de fase entre la corriente y el voltaje es CERO, como se muestra:

12. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RESISTIVO PURO
El diagrama de Fasores para este ejemplo nos muestra la relación de 𝐼𝑅 𝑦 𝑉𝑅 paralelos mientras
rotan en sentido antihorario
Ejem: para : ( Wt = (7/4)* π = 315º -- eje wt – antihorario )

13. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO CAPACITIVO PURO
La corriente adelanta 90° a la tensión.

14. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO CAPACITIVO PURO

15. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO CAPACITIVO PURO
Fig. 2 Fuente de AC
conectada a un
Capacitor
Aplicando la Ley de Mallas de Kirchhoff a este circuito se tiene:
𝜺 − 𝒗 𝑪 = 𝟎
es la caída de tensión en el
capacitor:
Para obtener la corriente despejamos «q» y derivamos respecto al tiempo:
Por tanto:
Donde:
Usando la relación: cos(wt)=sen(wt+(π/2), se obtiene lo siguiente:
Ic es la amplitud de la
corriente oscilante
….. (1)
….. (2)

16. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO CAPACITIVO PURO
Se conoce que en un
circuito resistivo:
Entonces por analogía definimos la
reactancia capacitiva como:
Por lo tanto , la amplitud de la corriente es:
Xc en Ω
XC- limita la corriente como lo hace una resistencia ;
sin embargo Xc depende de la frecuencia
Si comparamos la ecuación (1) con la (2) observamos que vc e ic se encuentran desfasadas
en (π/2) rad. El voltaje se encuentra retrasado 90º respecto dela corriente.

17. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO CAPACITIVO PURO
Ejem: para :
El voltaje se encuentra retrasado 90º respecto dela corriente, o que la corriente se adelanta
al voltaje en 90º
El diagrama de Fasores que se muestra, el fasor Vc va siempre (π /2) por detrás del fasor Ic.
315º
Fig. 2

18. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO INDUCTIVO PURO
La tensión adelanta 90° a la corriente.

19. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO INDUCTIVO PURO

20. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO INDUCTIVO PURO
Fig. 3 Fuente de AC
conectada a una
Inductancia
Aplicando la Ley de Mallas de Kirchhoff a este circuito se tiene:
Para obtener la corriente integramos a ecuación :
Por tanto:
Donde:
Ignorando los limites se obtiene lo siguiente: La constante de integración
representa una componente continua
de la corriente pero debe ser cero
….. (1)
….. (2)
Usando la relación: -cos(wt)=sen(wt+(π/2), se obtiene lo siguiente:
IL es la amplitud de la
corriente

21. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO INDUCTIVO PURO
Entonces por analogía con la resistencia y con la reactancia capacitiva
definimos la reactancia inductiva como:
Por lo tanto , la amplitud de la corriente es:
XL en Ω
XL- limita la corriente como lo hace una resistencia
y una Xc.
Si comparamos la ecuación (1) con la (2) observamos que vL e iL se encuentran desfasadas en (π/2)
rad con signo contario al del capacitivo. El voltaje se encuentra adelantado 90º respecto de la corriente.

22. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
VALORES ASOCIADOS A LAS ONDAS PERIÓDICAS
Ejem: para :
El voltaje se adelantado 90º respecto dela corriente, o que la corriente esta retrasado 90º
respecto al voltaje
El diagrama de Fasores que se muestra, el fasor VL va siempre (π /2) por delante del fasor IL.
315º
Fig. 3

23. LOGO
CIRCUITO RL SERIE
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.

24. LOGO
CIRCUITO RC SERIE
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.

25. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
IMPEDANCIA : INDUCTIVA Y CAPACITIVA

26. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RLC SERIE
XL

27. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RLC SERIE

28. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RLC SERIE RESONANTE

29. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RLC SERIE RESONANTE

30. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
CIRCUITO RLC SERIE - Aplicación
Un circuito RLC serie, donde R = 60 , XL = 90 , Xc = 10 , circula una corriente
de 1 Amperio. Hallar la tensión de la fuente y graficar los fasores de las tensiones.
Solución

31. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
Fr. Casares. (2010). Ondas De Señal: Onda Alterna Senoidal.
CIRCUITO RLC SERIE
Aplicando la Ley de Mallas de Kirchhoff a este circuito se tiene:
SUS VALORES MAXIMOS SON::
A partir de esta
ecuación se puede
calcular i y Ф:
También se `puede escribir:
…. (1)
(1) Se puede escribir como:

32. LOGO
CE II- - DRA. ING. MARGARITA MURILLO.
EXPOSICION 1.
CIRCUITOS RLC- PARALELO
Y
RESONANCIA PARALELO
LUNES 04 SETIEMBRE

33. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
Fr. Casares. (2010). Ondas De Señal: Onda Alterna Senoidal.
TAREA 2. Resolver (Hoja de problemas Nº 2
1. Una resistencia de 90 Ω, una bobina de 32 mH y
un condensador de 5 uF están conectados en
serie entre los terminales de una fuente de tensión
sinusoidal, como se muestra . La ecuación de régimen
permanente para la tensión de fuente es:
vs = 750 cos (5000t + 30°) V.
a) Construya el circuito equivalente en el dominio de la frecuencia.
b) Calcule la corriente de régimen permanente «i» mediante el método de fasores.
Solucion:

34. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
Fr. Casares. (2010). Ondas De Señal: Onda Alterna Senoidal.
TAREA 2. Revisar la solución de
1. Una resistencia de 90 Ω, una bobina de 32 mH y
un condensador de 5 uF están conectados en
serie entre los terminales de una fuente de tensión
sinusoidal, como se muestra . La ecuación de régimen
permanente para la tensión de fuente es:
vs = 750 cos (5000t + 30°) V.
a) Construya el circuito equivalente en el dominio de la frecuencia.
b) Calcule la corriente de régimen permanente «i» mediante el método de fasores.
Solucion:
a. A partir de la expresión correspondiente a «v» tenemos que w = 5000 rad/s. Por tanto, la impedancia
de la bobina de 32 mH es: ZL = jwL
ZL = j ( 5000 * 32 * 10- 3) = j l60 Ω
y la impedancia del condensador es :
ZC = j – 1/wC

35. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
Fr. Casares. (2010). Ondas De Señal: Onda Alterna Senoidal.
TAREA 2. Revisar la solución de
El fasor correspondiente a vs es:
el circuito equivalente en el dominio de l
frecuencia del circuito mostrado es:
b. Podemos calcular el fasor de corriente simplemente dividiendo la tensión de la fuente por la
impedancia equivalente que existe entre los terminales a y b , de acuerdo con la formula:
Zab = 90 + jl60 - j40
Zab = 90 + j 120 = 150/ 53,13° Ω
Por tanto,
Con esto podemos escribir directamente la
ecuación de régimen permanente para i:
i = 5 cos (5000t - 23,13°) A.
Zab = R + j X = |(R2+X2)1/2| artag(x/R)

36. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
Fr. Casares. (2010). Ondas De Señal: Onda Alterna Senoidal.
TAREA 2. Termine de Resolver
2.
Usar las siguientes formulas:
Utilizar las siguientes formulas
Zt= sqrt([(0.628^2)+(0.628^2)])=0,885 45º
Zt= 0.628+j0.628
b=Ф=arctag(R/XL) = arctag(0,628/0,628) = 45º
XL= 2 π fL=2*3,141516*60*2*10-3=j0.628 = 0,628 90º

37. LOGO
CICRUITOS ELECTRICOS II -DRA. ING. MARGARITA MURILLO.
Samchez, C. (2016). Circuitos RLC – Resonancia y Filtros Pasivos
TAREA 2. Resolver
3.

38. LOGO
Dra. ING. MARGARITA MURILLO MANRIQUE