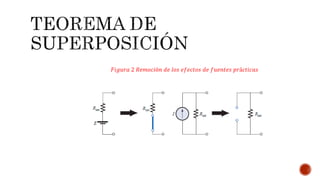
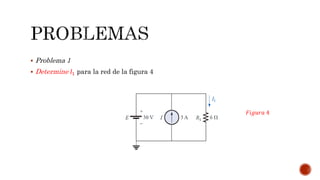
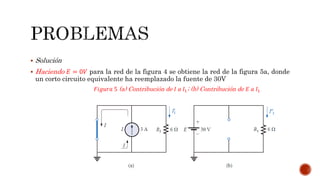
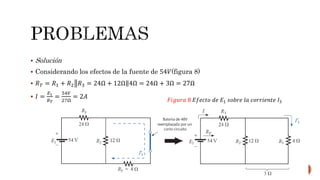
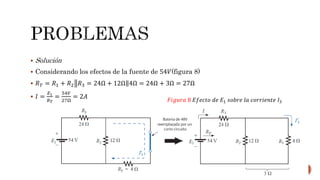
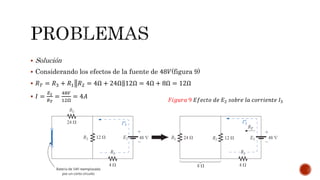
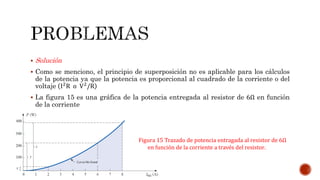
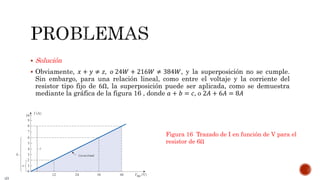
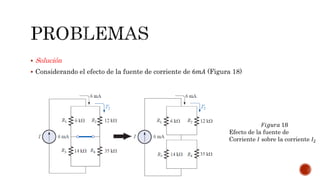
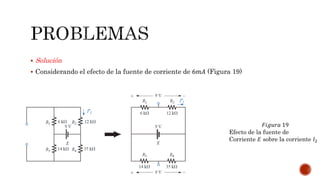
El documento describe el teorema de superposición y cómo puede usarse para encontrar las corrientes y voltajes en redes con múltiples fuentes. El teorema establece que la corriente o voltaje en un elemento es igual a la suma algebraica de los efectos de cada fuente considerada de forma independiente. Se explican los pasos para remover cada fuente y considerar sus efectos por separado antes de sumar los resultados. También se indica que la superposición no se aplica para cálculos de potencia debido a su naturaleza no lineal. Se incluyen