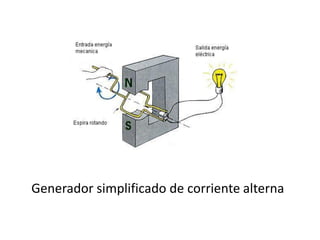
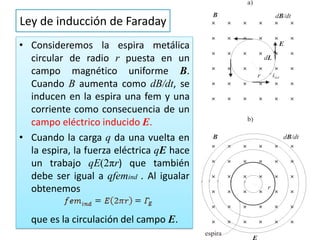
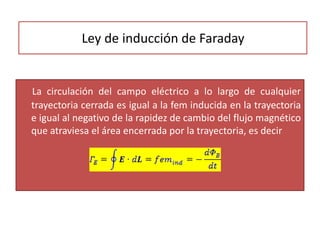
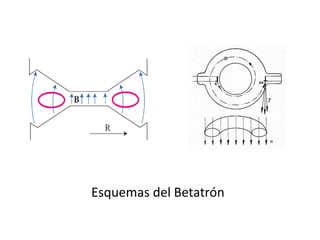
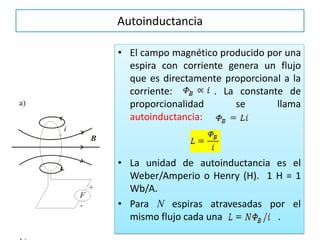
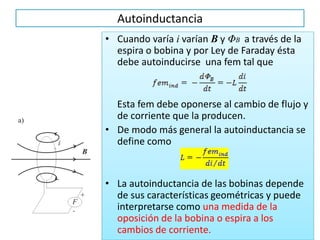
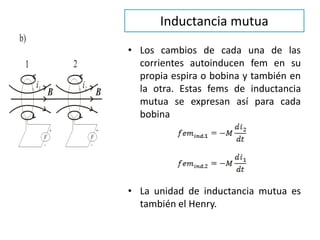
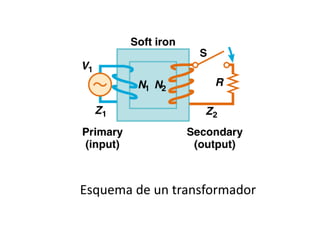
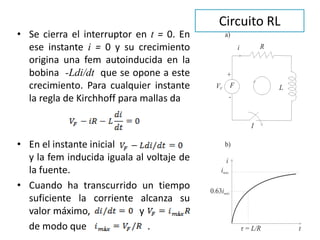
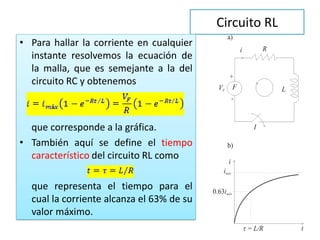
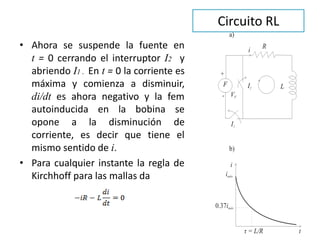
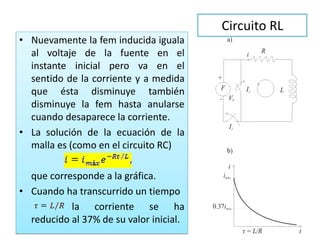
La inducción electromagnética se refiere al fenómeno por el cual una variación en un campo magnético induce una fuerza electromotriz en un circuito eléctrico cercano. La Ley de Inducción de Faraday establece que la fuerza electromotriz inducida en una espira es proporcional a la tasa de cambio del flujo magnético a través de la espira. La inducción electromagnética se aplica en dispositivos como generadores, motores eléctricos, transformadores de corriente y guitarras eléct

1. INDUCCIÓN DE FARADAY O
INDUCCIÓN ELECTROMAGNÉTICA
Experimentos de Faraday
Ley de inducción de Faraday
Autoinductancia e inductancia mutua
Circuitos RL
Energía almacenada en una bobina
Fundamentos E y M Darío M. Rodríguez G.

2. Preguntas orientadoras sobre Inducción de Faraday
• ¿Qué es la inducción electromagnética?
• ¿Cómo se enuncia la Ley de Inducción de Faraday?
• ¿En qué consiste la Ley de Lenz?
• ¿Cómo funciona un Betatrón?
• ¿Cómo se aplica la inducción electromagnética en una
guitarra eléctrica?
• ¿Cómo se define la autoinductancia de una bobina?
• ¿Qué es la inductancia mutua?
• ¿Cómo es un circuito RL?
• ¿Cuáles son las funciones para el establecimiento y la
disipación de la corriente en un circuito RL?
• ¿Cómo se expresa la energía almacenada en el campo
magnético de una bobina?

3. Trabajo autónomo
• Consultar los materiales de Referencia citados en el Programa
de la asignatura.
• Hacer los ejercicios sobre Inducción electromagnética que se
encuentran en el Aula Virtual.
• Ver y discutir el video N°38 (Corrientes alternas) de la serie “El
universo mecánico”. Enlace:
• https://youtu.be/MmVqRnhWYKo?list=PLu11ymT_JYRou9nGs
JdV8-5pgLbmMaiNP
• Buscar respuestas iniciales a las preguntas orientadoras sobre
Circuitos de corriente alterna y ver las diapositivas
correspondientes a la clase siguiente.

4. Experimentos de Faraday
• Desplazamiento relativo de
bobinas e imanes.
Cuando hay movimiento
relativo aparece una corriente
inducida en la bobina, que
depende directamente de la
rapidez del movimiento y que
cambia de sentido al invertir la
dirección de movimiento del
imán o al invertir su polaridad.

5. Experimento de Faraday

6. Experimentos de Faraday
• Al reemplazar el imán por una
bobina con corriente estacionaria
se obtienen resultados semejantes.
• Variación de corriente.
No hay mov. relativo. Aparece la
corriente inducida sólo al cerrar o
abrir el interruptor o al variar la
corriente directa.
La corriente inducida depende
directamente de la rapidez de
variación de i y cambia de sentido
al aumentar o disminuir i o al
invertir la polaridad de la fuente.

7. Experimentos de Faraday
• Variación del área de
espiras o bobinas.
Aparece la corriente
inducida sólo al variar el
área de bobinas o espiras
deformables, tiene sentidos
opuestos para el aumento
o la disminución y depende
directamente de la rapidez
del cambio del área.

8. Experimentos de Faraday
• Rotación de una bobina.
No hay desplazamiento lineal
relativo ni deformación de la
bobina.
Se induce en la bobina una
corriente alterna con la misma
frecuencia de giro y con una
intensidad instantánea que
depende directamente de la
frecuencia de giro de la bobina.

9. Generador simplificado de corriente alterna

10. Ley de inducción de Faraday
• En los experimentos anteriores la corriente inducida depende
directamente de la rapidez de variación del campo magnético
exterior o del área de la bobina o de la orientación de la bobina
con respecto al campo exterior.
• Faraday propuso que la corriente inducida depende directamente
de la rapidez de variación del flujo magnético que atraviesa la
bobina y que esta corriente inducida es producida por una fem
inducida en la bobina tal que
• Notemos que las unidades de la rapidez de variación del flujo
magnético son Weber/segundo = Voltio y que si el flujo
magnético es constante, la fem y la corriente inducidas son
iguales a cero.

11. Ley de inducción de Faraday
• El signo negativo en la Ley
de Faraday se refiere a la
llamada Ley de Lenz:
“La fem inducida en un
circuito cerrado tiene un
sentido tal que la corriente
inducida se opone al
cambio del flujo magnético
que la origina”.

12. Ley de inducción de Faraday
• Consideremos la espira metálica
circular de radio r puesta en un
campo magnético uniforme B.
Cuando B aumenta como dB/dt, se
inducen en la espira una fem y una
corriente como consecuencia de un
campo eléctrico inducido E.
• Cuando la carga q da una vuelta en
la espira, la fuerza eléctrica qE hace
un trabajo qE(2πr) que también
debe ser igual a qfemind . Al igualar
obtenemos
que es la circulación del campo E.

13. Ley de inducción de Faraday
• La identificación de la fem inducida con
la circulación del campo eléctrico
inducido es un resultado de validez
general que se cumple para cualquier
campo eléctrico inducido y para
cualquier trayectoria cerrada de
integración.
• Este campo es muy diferente del
producido por cargas pues para éste
. El campo eléctrico
inducido es un campo no conservativo,
de líneas cerradas, originado por la
variación temporal del flujo magnético.

14. Ley de inducción de Faraday
La circulación del campo eléctrico a lo largo de cualquier
trayectoria cerrada es igual a la fem inducida en la trayectoria
e igual al negativo de la rapidez de cambio del flujo magnético
que atraviesa el área encerrada por la trayectoria, es decir

15. Ley de inducción de Faraday
• Si la circulación del campo eléctrico es diferente de cero hay
campo eléctrico inducido y debe haber variación temporal del
flujo magnético.
• La circulación del campo eléctrico producido por cargas
eléctricas es siempre igual a cero.
• La existencia de fem inducida no implica que deben existir
corrientes inducidas; éstas se presentan cuando hay cargas
móviles disponibles como en una espira metálica o en un
Betatrón.
• El Betatrón es un acelerador de electrones cuyo
funcionamiento depende del campo eléctrico inducido en el
espacio alrededor de un campo magnético variable en el
tiempo.

16. Esquemas del Betatrón

17. Inducción e-m en una guitarra eléctrica

18. Autoinductancia
• El campo magnético producido por una
espira con corriente genera un flujo
que es directamente proporcional a la
corriente: . La constante de
proporcionalidad se llama
autoinductancia:
• La unidad de autoinductancia es el
Weber/Amperio o Henry (H). 1 H = 1
Wb/A.
• Para N espiras atravesadas por el
mismo flujo cada una .

19. Autoinductancia
• Cuando varía i varían B y ΦB a través de la
espira o bobina y por Ley de Faraday ésta
debe autoinducirse una fem tal que
Esta fem debe oponerse al cambio de flujo y
de corriente que la producen.
• De modo más general la autoinductancia se
define como
• La autoinductancia de las bobinas depende
de sus características geométricas y puede
interpretarse como una medida de la
oposición de la bobina o espira a los
cambios de corriente.

20. Detector de metales por variación de autoinductancia

21. Inductancia mutua
• Si dos espiras o bobinas con corrientes
i1 e i2 están próximas, el flujo
magnético a través de cada una es
proporcional a su propia corriente y a la
de la otra espira o bobina, de modo que
donde M es la inductancia mutua o
inductancia de cada bobina con
respecto a la otra.
Puede demostrarse que

22. Inductancia mutua
• Los cambios de cada una de las
corrientes autoinducen fem en su
propia espira o bobina y también en
la otra. Estas fems de inductancia
mutua se expresan así para cada
bobina
• La unidad de inductancia mutua es
también el Henry.

23. Esquema de un transformador

24. Circuito RL
• Se cierra el interruptor en t = 0. En
ese instante i = 0 y su crecimiento
origina una fem autoinducida en la
bobina -Ldi/dt que se opone a este
crecimiento. Para cualquier instante
la regla de Kirchhoff para mallas da
• En el instante inicial
y la fem inducida iguala al voltaje de
la fuente.
• Cuando ha transcurrido un tiempo
suficiente la corriente alcanza su
valor máximo, y
de modo que .

25. Circuito RL
• Para hallar la corriente en cualquier
instante resolvemos la ecuación de
la malla, que es semejante a la del
circuito RC y obtenemos
que corresponde a la gráfica.
• También aquí se define el tiempo
característico del circuito RL como
que representa el tiempo para el
cual la corriente alcanza el 63% de su
valor máximo.

26. Circuito RL
• Ahora se suspende la fuente en
t = 0 cerrando el interruptor I2 y
abriendo I1 . En t = 0 la corriente es
máxima y comienza a disminuir,
di/dt es ahora negativo y la fem
autoinducida en la bobina se
opone a la disminución de
corriente, es decir que tiene el
mismo sentido de i.
• Para cualquier instante la regla de
Kirchhoff para las mallas da

27. Circuito RL
• Nuevamente la fem inducida iguala
al voltaje de la fuente en el
instante inicial pero va en el
sentido de la corriente y a medida
que ésta disminuye también
disminuye la fem hasta anularse
cuando desaparece la corriente.
• La solución de la ecuación de la
malla es (como en el circuito RC)
que corresponde a la gráfica.
• Cuando ha transcurrido un tiempo
la corriente se ha
reducido al 37% de su valor inicial.

28. Energía magnética almacenada en una bobina
• Tomamos la ecuación de la regla de mallas
y la multiplicamos
por i para obtener una ec. de potencias:
donde es la potencia eléctrica
producida en la fuente, es la potencia
consumida en la resistencia e
debe ser la potencia consumida o
almacenada en la bobina.
• Esta potencia consumida en la bobina se
considera almacenada en el campo
magnético y puede expresarse como

29. Energía magnética almacenada en una bobina
• Entonces a partir de i = 0 y hasta
alcanzar la i máxima, la energía
magnética almacenada en la bobina es
• Cuando una bobina conduce una
corriente i la energía almacenada en
el campo magnético es
• Esta energía puede recuperarse como
calor en la resistencia al quitar la
fuente o puede transformarse en otras
formas de energía (proyecto de autos
eléctricos con bobinas superconduct.).