Descargado 62 veces
Subido porRocio Chavez
Clustering K-Means
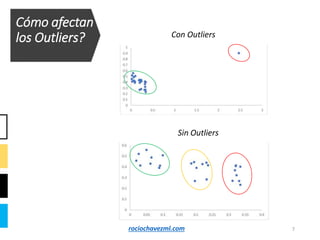
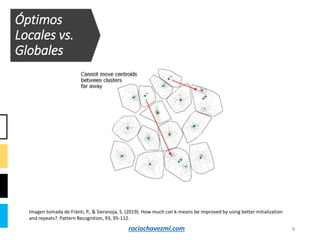
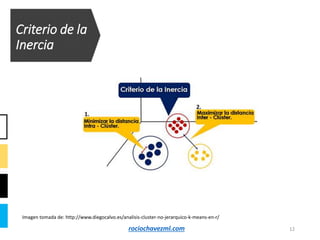
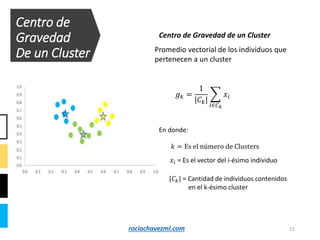
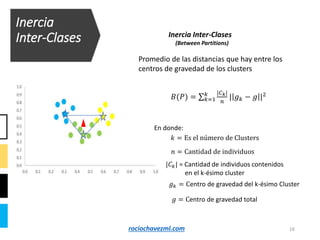
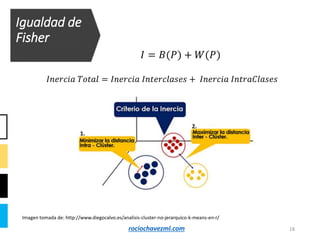
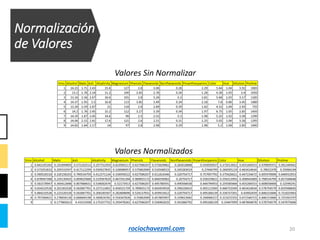
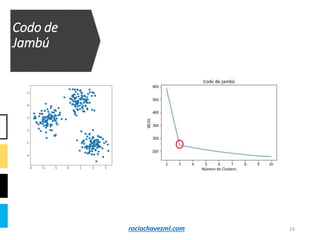
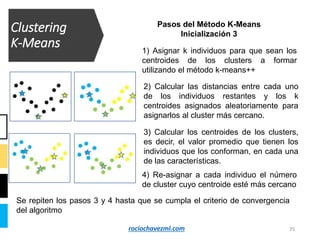
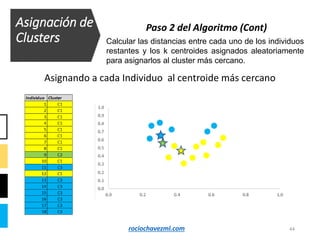
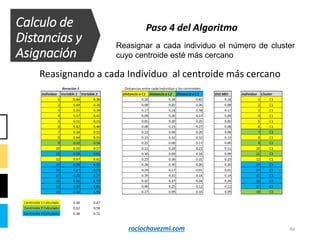
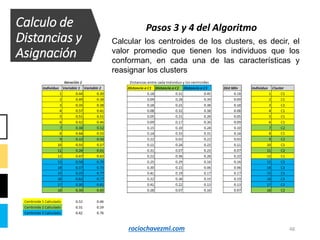
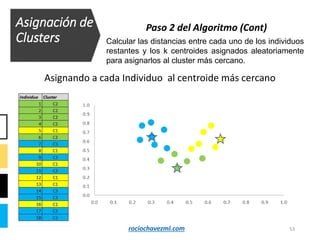
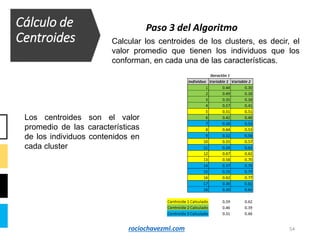
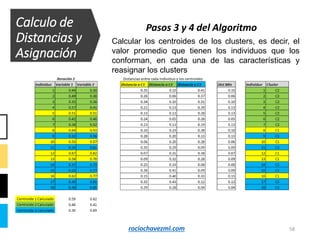
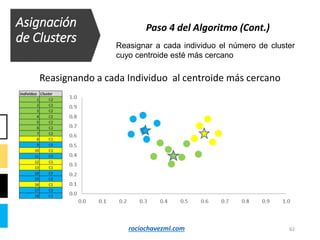
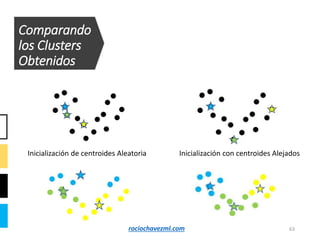
El documento detalla el método de clustering k-means, enfatizando sus aplicaciones y variaciones, así como sus ventajas y desventajas. Se abordan aspectos como la determinación del número de clusters, la cohesión y separación, y técnicas de normalización y eliminación de outliers. Además, se describen pasos y estrategias para optimizar la inicialización del algoritmo y los criterios de convergencia.
Clustering K-Means
- 1. Método de lasK-Medias Clustering No Jerárquico 1 IT PhD Rocío Chávez rociochavezml.com
- 2. Temas - Algoritmo K-Means -Ventajas y Desventajas - Algunas variantes del K-Means - Algunas técnicas para determinar la cantidad de clusters - Cohesión y separación de Clusters - Acciones previas al análisis con k-Means - Diferentes formas de inicializar el algoritmo - Ejemplo numérico con centroides iniciales cercanos - Ejemplo numérico con centroides iniciales alejados rociochavezml.com
- 3. SEGMENTACIÓN DE CLIENTES PARACAMPAÑAS DE MARKETING DETECCIÓN DE GENES QUE SE COMPORTAN DE LA MISMA MANERA ANÁLISIS DE RELACIONES EN LAS REDES SOCIALES AGRUPACIÓN DE DOCUMENTOS RECOMENDACIONES MUSICALES O DE CONTENIDOS Usos del Aprendizaje No Supervisado rociochavezml.com
- 4. Clustering K-Means 4 Método no supervisadoque sirve para hacer agrupaciones de objetos o individuos en base a la similitud de sus características Se busca formar clusters compactos y bien definidos rociochavezml.com
- 5. Ventajas Es fácil deimplementar Es útil cuando queremos segmentar grandes volúmenes de datos (Cuando se trata de big data se utilizan variantes como el Mini-Batch K-Means) Computacionalmente es menos costoso que el clustering Jerárquico Ha sido ampliamente utilizado en bases de datos reales con buenos resultados 5rociochavezml.com
- 6. Desventajas Necesitamos conocer deantemano la cantidad de clusters a formar Debido a que crea los grupos en base a las distancias entre los individuos, solamente maneja variables numéricas. La calidad de los clusters depende en gran medida de los valores con los que se inicializa el algoritmo Puede ser que se obtenga un resultado que sea óptimo localmente pero no globalmente El resultado se vé muy afectado por los outliers 6rociochavezml.com
- 7. Cómo afectan los Outliers? 7 ConOutliers Sin Outliers rociochavezml.com
- 8. Óptimos Locales vs. Globales 8 Imagen tomadade Fränti, P., & Sieranoja, S. (2019). How much can k-means be improved by using better initialization and repeats?. Pattern Recognition, 93, 95-112. rociochavezml.com
- 9. Algunas Variantes de K-Means K-Modas: - Utilizamodas en lugar de medias - Maneja Variables Categóricas K-Medoids: - Es más robusto al ruido y a los valores atípicos - En lugar de utilizar centroides, utiliza individuos que se encuentran más centrados con respecto al cluster (medianas) Mini-Batch K-Means: Utilizado en Big Data - Divide las bases de datos en subconjuntos que se van procesando en cada paso del algoritmo 9rociochavezml.com
- 10. Cuando No es óptimo K-Means? 10 Paramás información visita https://scikit-learn.org/stable/auto_examples/cluster/plot_cluster_comparison.html Clusters de diferentes tamaños, formas y densidades rociochavezml.com
- 11. Cohesión y Separación de Clusters 11 Cohesión Separación Midela cohesión que hay en los clusters, es decir, distancia que hay entre un individuo y los demás individuos que se encuentran en un mismo cluster (Distancia Intra-Cluster) Mide la distancia que hay entre individuos se encuentran en clusters diferentes. (Distancia Inter-Cluster) rociochavezml.com
- 12. Criterio de la Inercia 12 Imagentomada de: http://www.diegocalvo.es/analisis-cluster-no-jerarquico-k-means-en-r/ rociochavezml.com
- 13. Centro de Gravedad Total 13 𝑔 = 1 𝑛 𝑖=1 𝑛 𝑥𝑖 Endonde: 𝑥𝑖 = Es el vector del i-ésimo individuo Promedio vectorial de todos los individuos Centro de Gravedad Total 𝑛 = Cantidad de individuos 𝑔 rociochavezml.com
- 14. Inercia Total 14 En donde: 𝑥𝑖 =Es el vector del i-ésimo individuo Promedio de las distancias que hay entre los individuos y el centro de gravedad total InerciaTotal 𝐼 = 1 𝑛 𝑖=1 𝑛 ||𝑥𝑖 − 𝑔||2 𝑔 = Centro de gravedad total 𝑛 = Cantidad de individuos rociochavezml.com
- 15. Centro de Gravedad De unCluster 15 Centro de Gravedad de un Cluster En donde: 𝑥𝑖 = Es el vector del i-ésimo individuo 𝑘 = Es el número de Clusters 𝑔 𝑘 = 1 |𝐶 𝑘| 𝑖∈𝐶 𝑘 𝑥𝑖 Promedio vectorial de los individuos que pertenecen a un cluster |𝐶 𝑘| = Cantidad de individuos contenidos en el k-ésimo cluster rociochavezml.com
- 16. Inercia Inter-Clases 16 Inercia Inter-Clases (Between Partitions) Endonde: 𝑛 = Cantidad de individuos Promedio de las distancias que hay entre los centros de gravedad de los clusters |𝐶 𝑘| = Cantidad de individuos contenidos en el k-ésimo cluster 𝐵(𝑃) = 𝑘=1 𝑘 |𝐶 𝑘| 𝑛 | 𝑔 𝑘 − 𝑔 |2 𝑔 = Centro de gravedad total 𝑔 𝑘 = Centro de gravedad del k-ésimo Cluster 𝑘 = Es el número de Clusters rociochavezml.com
- 17. Inercia Intra-Clases 17 Inercia Intra-Clases (Within Partitions) Endonde: Promedio de las distancias que hay entre los individuos y el centro de gravedad del cluster al que pertenecen 𝑊 𝑃 = 1 𝑛 𝑘=1 𝑘 𝑖∈𝐶 𝑘 | 𝑥𝑖 − 𝑔 𝑘 |2 𝑛 = Cantidad de individuos 𝑔 𝑘 = Centro de gravedad del k-ésimo Cluster 𝑘 = Es el número de Clusters 𝑥𝑖 = Es el vector del i-ésimo individuo 𝐶 𝑘 = Es el k-ésimo cluster rociochavezml.com
- 18. Igualdad de Fisher 18 𝐼𝑛𝑒𝑟𝑐𝑖𝑎 𝑇𝑜𝑡𝑎𝑙= 𝐼𝑛𝑒𝑟𝑐𝑖𝑎 𝐼𝑛𝑡𝑒𝑟𝑐𝑙𝑎𝑠𝑒𝑠 + 𝐼𝑛𝑒𝑟𝑐𝑖𝑎 𝐼𝑛𝑡𝑟𝑎𝐶𝑙𝑎𝑠𝑒𝑠 𝐼 = 𝐵(𝑃) + 𝑊(𝑃) Imagen tomada de: http://www.diegocalvo.es/analisis-cluster-no-jerarquico-k-means-en-r/ rociochavezml.com
- 19. Acciones Previas para K-Means - RemoverOutliers - Normalizar valores en caso de que estos no sean comparables - Determinar la cantidad de Clusters a formar 19rociochavezml.com
- 20. Normalización de Valores 20 Valores SinNormalizar Valores Normalizados rociochavezml.com
- 21. 21 La cantidad declusters a crear puede depender entre otras cosas de: Cantidad de Clusters a crear La estrategia del negocio Las limitaciones del sistema que estamos analizando Técnicas de validación de clusters Sin información previa: rociochavezml.com
- 22. 22 ANALISIS DE COMPONENTESPRINCIPALES Visualización de los datos Valores Normalizados rociochavezml.com
- 23. 23 Codo de Jambú Coeficientede Silueta Indice de Dunn Técnicas para Determinar la cantidad de Clusters Aplicar Clustering Jerárquico a una muestra tomada aleatoriamente Davies-Bouldin Index rociochavezml.com
- 24.
- 25.
- 26. 26 Coeficiente de Silueta Clusters 2y 3 rociochavezml.com
- 27. 27 Coeficiente de Silueta Clusters 2y 3 10 8 16 13 12 9 14 11 17 18 15 5 7 4 3 6 1 2 Silhouette width si 0.0 0.2 0.4 0.6 0.8 1.0 Silhouette plot of (x = k3$cluster, dist = distancias.Ejemplo_est) Average silhouette width : 0.45 n = 18 3 clusters Cj j : nj | avei Cj si 1 : 7 | 0.41 2 : 6 | 0.50 3 : 5 | 0.45 13 9 16 11 18 14 15 17 7 12 10 3 8 6 5 1 4 2 Silhouette width si 0.0 0.2 0.4 0.6 0.8 1.0 Silhouette plot of (x = k2$cluster, dist = distancias.Ejemplo_es Average silhouette width : 0.36 n = 18 2 clusters Cj j : nj | avei Cj si 1 : 10 | 0.40 2 : 8 | 0.30 Este elemento se encuentra en el límite entre los dos clusters rociochavezml.com
- 28.
- 29.
- 30.
- 31. 31 Cuando no existe nicohesión ni separación grandes rociochavezml.com
- 32. 32 Pasos del AlgoritmoK-Means y Tres Formas Diferentes de Inicializarlo rociochavezml.com
- 33. Clustering K-Means Pasos del MétodoK-Means Inicialización 1 33 3) Asignar a cada individuo el número de cluster cuyo centroide esté más cercano 2) Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características. 1) Asignar aleatoriamente un número de cluster a cada individuo. Se repiten los pasos 2 y 3 hasta que se cumpla el criterio de convergencia del algoritmo Imagen tomada de: James, Gareth, et al. An introduction to statistical learning. Vol. 112. New York: springer, 2013. rociochavezml.com
- 34. Clustering K-Means Pasos del MétodoK-Means Inicialización 2 34 4) Re-asignar a cada individuo el número de cluster cuyo centroide esté más cercano 2) Calcular las distancias entre cada uno de los individuos restantes y los k centroides asignados aleatoriamente para asignarlos al cluster más cercano. 1) Asignar aleatoriamente k individuos para que sean los centroides de los clusters a formar. Se repiten los pasos 3 y 4 hasta que se cumpla el criterio de convergencia del algoritmo 3) Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características. rociochavezml.com
- 35. Clustering K-Means Pasos del MétodoK-Means Inicialización 3 35 4) Re-asignar a cada individuo el número de cluster cuyo centroide esté más cercano 2) Calcular las distancias entre cada uno de los individuos restantes y los k centroides asignados aleatoriamente para asignarlos al cluster más cercano. 1) Asignar k individuos para que sean los centroides de los clusters a formar utilizando el método k-means++ Se repiten los pasos 3 y 4 hasta que se cumpla el criterio de convergencia del algoritmo 3) Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características. rociochavezml.com
- 36. 36 Imágenes tomadas dehttps://www.analyticsvidhya.com/blog/2019/08/comprehensive-guide-k-means- clustering/#k-means-clustering-python-code Datos a Agrupar Primer Centroide Segundo Centroide Tercer Centroide Distancias entre los puntos y el centroide Distancias entre cada punto y su centroide más cercano Asignando los centroides con K-Means++ rociochavezml.com
- 37. Criterios de Convergencia 37 2) Elvalor de la inercia intra-clases es menor a un valor de tolerancia dado 1) Los individuos ya no son reasignados a otro cluster 3) Se lleva a cabo una cantidad determinada de iteraciones rociochavezml.com
- 38. 38 Ejemplos Numéricos Inicializaciones 2y 3 del Algoritmo K-Means rociochavezml.com
- 39.
- 40. 40 Ejemplo Numérico Inicialización 2 delAlgoritmo K-Means rociochavezml.com
- 41. 41 Asignación de Centroides Asignar aleatoriamentek individuos para que sean los centroides de los clusters a formar. Paso 1 del Algoritmo rociochavezml.com
- 42. 42 Distancia Euclidea entreel Individuo 1 y los 3 Centroides asignados aleatoriamente Distancia a los centroides Calcular las distancias entre cada uno de los individuos restantes y los k centroides asignados aleatoriamente para asignarlos al cluster más cercano. Paso 2 del Algoritmo rociochavezml.com
- 43. 43 Distancia entre cadaIndividuo y los 3 Centroides asignados aleatoriamente Cálculo de Distancias Calcular las distancias entre cada uno de los individuos restantes y los k centroides asignados aleatoriamente para asignarlos al cluster más cercano. Paso 2 del Algoritmo (Cont) rociochavezml.com
- 44. 44 Asignando a cadaIndividuo al centroide más cercano Asignación de Clusters Calcular las distancias entre cada uno de los individuos restantes y los k centroides asignados aleatoriamente para asignarlos al cluster más cercano. Paso 2 del Algoritmo (Cont) rociochavezml.com
- 45. 45 Cálculo de Centroides Paso 3del Algoritmo Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características. rociochavezml.com
- 46. 46 Reasignando a cadaIndividuo al centroide más cercano Calculo de Distancias y Asignación Paso 4 del Algoritmo Reasignar a cada individuo el número de cluster cuyo centroide esté más cercano rociochavezml.com
- 47. 47 Reasignando a cadaIndividuo al centroide más cercano Asignación de Clusters Paso 4 del Algoritmo (Cont.) Reasignar a cada individuo el número de cluster cuyo centroide esté más cercano rociochavezml.com
- 48. 48 Calculo de Distancias y Asignación Pasos3 y 4 del Algoritmo Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características y reasignar los clusters rociochavezml.com
- 49. 49 Reasignando a cadaIndividuo al centroide más cercano Asignación de Clusters Paso 4 del Algoritmo (Cont.) Reasignar a cada individuo el número de cluster cuyo centroide esté más cercano rociochavezml.com
- 50. 50 Ejemplo Numérico Inicialización 3 delAlgoritmo K-Means rociochavezml.com
- 51. 51 Utilizando centroides inicialesalejados Cálculo de Distancias Asignar k individuos para que sean los centroides de los clusters a formar utilizando el método k- means++ Paso 1 del Algoritmo rociochavezml.com
- 52. 52 Distancia entre cadaIndividuo y los 3 Centroides asignados inicialmente Calculo de Distancias y Asignación Calcular las distancias entre cada uno de los individuos restantes y los k centroides asignados aleatoriamente para asignarlos al cluster más cercano. Paso 2 del Algoritmo rociochavezml.com
- 53. 53 Asignando a cadaIndividuo al centroide más cercano Asignación de Clusters Calcular las distancias entre cada uno de los individuos restantes y los k centroides asignados aleatoriamente para asignarlos al cluster más cercano. Paso 2 del Algoritmo (Cont) rociochavezml.com
- 54. 54 Cálculo de Centroides Paso 3del Algoritmo Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características. Los centroides son el valor promedio de las características de los individuos contenidos en cada cluster rociochavezml.com
- 55. 55 Reasignando a cadaIndividuo al centroide más cercano Calculo de Distancias y Asignación Paso 4 del Algoritmo Reasignar a cada individuo el número de cluster cuyo centroide esté más cercano rociochavezml.com
- 56. 56 Asignación del Cluster Reasignando acada Individuo al centroide más cercano Paso 4 del Algoritmo (Cont.) Reasignar a cada individuo el número de cluster cuyo centroide esté más cercano rociochavezml.com
- 57. 57 Cálculo de Centroides Paso 3del Algoritmo Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características. rociochavezml.com
- 58. 58 Calculo de Distancias y Asignación Pasos3 y 4 del Algoritmo Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características y reasignar los clusters rociochavezml.com
- 59. 59 Reasignando a cadaIndividuo al centroide más cercano Asignación de Clusters Paso 4 del Algoritmo (Cont.) Reasignar a cada individuo el número de cluster cuyo centroide esté más cercano rociochavezml.com
- 60. 60 Cálculo de Centroides Paso 3del Algoritmo Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características. rociochavezml.com
- 61. 61 Calculo de Distancias y Asignación Pasos3 y 4 del Algoritmo Calcular los centroides de los clusters, es decir, el valor promedio que tienen los individuos que los conforman, en cada una de las características y reasignar los clusters rociochavezml.com
- 62. 62 Reasignando a cadaIndividuo al centroide más cercano Asignación de Clusters Paso 4 del Algoritmo (Cont.) Reasignar a cada individuo el número de cluster cuyo centroide esté más cercano rociochavezml.com
- 63. 63 Comparando los Clusters Obtenidos Inicialización decentroides Aleatoria Inicialización con centroides Alejados rociochavezml.com