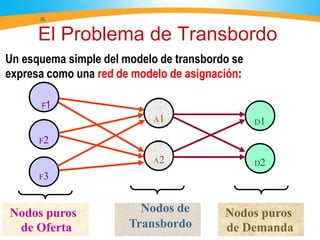
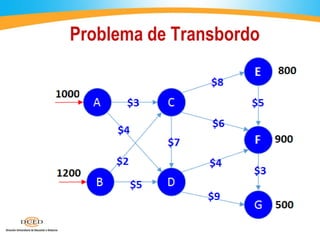
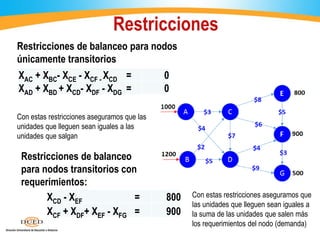
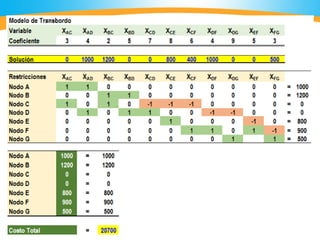
El documento describe el problema de transbordo, donde se reconoce mediante el uso de nodos intermedios o transitorios para el envío de recursos entre fuentes y destinos. Se construye una malla con nodos de oferta, demanda y transbordo, unidos por arcos que representan flujos. El problema se resuelve como un modelo de transporte usando amortiguadores en los nodos transitorios, o directamente mediante programación lineal usando restricciones de balance en los nodos.

1. CHAMBERGO GARCIA,
ALEJANDRO
INVESTIGACIÓN DE OPERACIONES II
Módulo: II Unidad: III Semana: 6

2. Transbordo

3. El Problema de Transbordo
• El Problema de Transbordo,
Intertransporte o Reembarque es una
variación del modelo original de transporte que
se ajusta a la posibilidad común de transportar
unidades mediante nodos fuentes, destinos y
transitorios, mientras el modelo tradicional solo
permite envíos directos desde nodos fuentes
hacia nodos destinos.

4. El Problema de Transbordo
• Existe la posibilidad de resolver un modelo de
transbordo mediante las técnicas tradicionales de
resolución de modelos de transporte y este
procedimiento se basa en la preparación del
tabulado inicial haciendo uso de artificios
conocidos con el nombre
de amortiguadores, los cuales deben ser
iguales a la sumatoria de las ofertas de los nodos
de oferta pura y de coeficiente cero (0) en
materia de costos.

5. El Problema de Transbordo
• Sin embargo la resolución de un problema de
transbordo haciendo uso de los algoritmos de
resolución de modelos de transporte es una idea
anacrónica, teniendo en cuenta la posibilidad de
acceso a herramientas de cómputo (como
Solver) capaces de resolver problemas
complejos una vez modelados mediante las
técnicas de programación lineal.

6. El Problema de Transbordo
• La importancia de los modelos de transbordo
aumenta con las nuevas tendencias globales de
gestión de cadenas de abastecimiento, en las
cuales se deben de optimizar los flujos logísticos
de productos teniendo en cuenta la importancia
de minimizar los costos, asegurar disponibilidad
de unidades y reconociendo la importancia de los
centros de distribución en la búsqueda del
equilibrio entre las proyecciones y la realidad de
la demanda.

7. El Problema de Transbordo

8. El Problema de Transbordo
Se reconoce mediante el uso de nodos intermedios o
transitorios para el envío de recursos entre las
distintas fuentes (oferta) y destinos (demanda)
Se construye una malla con orientación desde las
fuentes (nodos de inicio) hacia los destinos (nodos de
llegada), utilizando amortiguadores (nodos transitorios)
que permiten recibir y transferir recursos. Las flechas
que unen los nodos de la malla representan los
eventuales flujos de recursos en la secuencia de
distribución

9. El Problema de Transbordo
Luego, la malla permite convertir un modelo de
transbordo en un modelo de transporte regular y
resolverse como tal, utilizando los amortiguadores
Así, la malla reconoce tres tipos de nodos:
• Nodos puros de Oferta: solo transfieren recursos
• Nodos de Transbordo: entregan y reciben recursos
• Nodos puros de Demanda: solo reciben recursos
El amortiguador debe ser suficientemente grande para
permitir que los recursos se transfieran desde las
fuentes hacia los destinos

10. El Problema de Transbordo
D1
D2
Nodos puros
de Oferta
Nodos puros
de Demanda
A1
A2
RL
Un esquema simple del modelo de transbordo se
expresa como una red de modelo de asignación:
F1
F2
F3
Nodos de
Transbordo

11. El Problema de Transbordo
P1 P2,
RL
Dos fábricas de automóviles, y están
conectadas a tres distribuidores, D1, D2 y D3, por
medio de dos centros de tránsito, T1 y T2, de acuerdo
con la red que se muestra en la siguiente diapositiva.
Las cantidades de la oferta en las fábricas P1 y P2, son
de 1000 y 1200 automóviles, y las cantidades de la
demanda en las distribuidoras D1, D2 y D3, son de 800,
900 y 500 automóviles. El costo de envío por automóvil
(en cientos de soles) entre los pares de nodos, se
muestra en los arcos de conexión de la red.

12. Problema de Transbordo

13. Solución del Problema de Transbordo
• Para poder resolver un problema de transbordo mediante
programación lineal basta con conocer una nueva familia de
restricciones, las llamadas restricciones de balanceo.
• En un problema de transbordo existen 3 clases de nodos,
los nodos de oferta pura, los de demanda pura y los nodos
transitorios que posibilitan el transbordo y que deben de
balancearse para hacer que el sistema sea viable, es decir,
que todas las unidades que ingresen a un nodo sean
iguales a las que salgan del mismo (unidades que salen +
unidades que conserve el nodo).

14. Solución del Problema de Transbordo
• La figura muestra una serie de nodos y sus
respectivas rutas mediante las cuales se supone
distribuir las unidades de un producto, el número
que lleva cada arco (flecha) representa el costo
unitario asociado a esa ruta (arco), y las
cantidades que se ubican en los nodos iniciales
representan la oferta de cada planta, así como
las cantidades de los nodos finales representa la
demanda de cada distribuidor

15. Variables de decisión
• En este caso como en la mayoría las variables de
decisión deben representar la cantidad de unidades
enviadas por medio de cada ruta.

16. Restricciones
• Existen en este modelo 3 tipos de restricciones y están
estrechamente relacionadas con los tipos de nodos
existentes, para un nodo oferta pura existe la restricción
de oferta; para un nodo demanda pura existe la
restricción de demanda, y para un nodo transitorio y/o
transitorio de demanda existe la restricción de balance
• Recordemos que los nodos transitorios son aquellos que
tienen rutas (arcos o flechas) de entrada y salida, y si
además este presenta un requerimiento de unidades se
denomina transitorio de demanda

17. Restricciones
• Restricciones de
Oferta:
• Restricciones de
Demanda:
XAC + XAD = 1000
XBC + XBD = 1200
XDG + XFG = 500

18. Restricciones
Restricciones de balanceo para nodos
únicamente transitorios
Restricciones de balanceo
para nodos transitorios con
requerimientos:
XAC + XBC- XCE - XCF - XCD = 0
XAD + XBD + XCD- XDF - XDG = 0
Con estas restricciones aseguramos que las
unidades que lleguen sean iguales a las
unidades que salgan
XCD - XEF = 800
XCF + XDF+ XEF - XFG = 900
Con estas restricciones aseguramos que
las unidades que lleguen sean iguales a
la suma de las unidades que salen más
los requerimientos del nodo (demanda)

19. Min = 3XAC + 4XAD + 2XBC + 5XBD + 7XCD + 8XCE + 6XCF + 4XDF + 9XDG + 5XEF + 3XFG
Función Objetivo
• En este caso la definición de la función objetivo se limita
a la consignación de cada ruta con su respectivo costo
bajo el criterio "minimizar".

21. GRACIAS