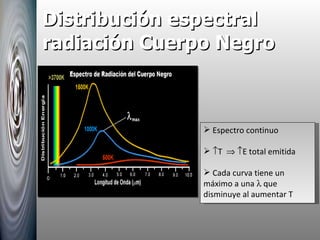
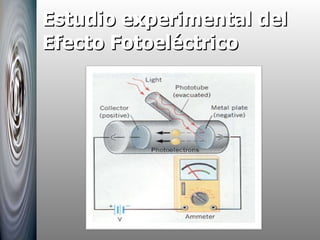
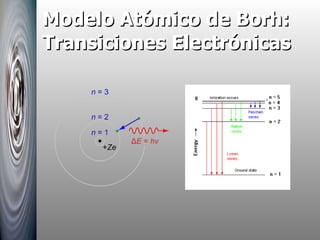
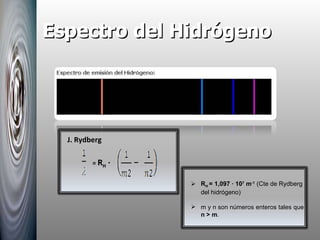
El documento resume las principales contribuciones al desarrollo de la física cuántica, incluyendo la hipótesis de Planck sobre la cuantización de la energía, la interpretación del efecto fotoeléctrico por Einstein, el modelo atómico de Bohr y su explicación de los espectros atómicos, y la hipótesis de De Broglie sobre la dualidad onda-corpúsculo.

1. Derrumbamiento Física Clásica La nueva concepción del mundo

2. Contenidos

3. Radiación térmica Radicación : es la energía que emiten todos los cuerpos en forma de onda electromagnética como consecuencia de su estado térmico

4. Distribución espectral radiación Cuerpo Negro Espectro continuo  T   E total emitida Cada curva tiene un máximo a una  que disminuye al aumentar T

5. Ley Stefan-Boltzman y Ley de Wien W =  ·T 4 = 5,6687 · 10 -8 W m -2 K -4 (Cte de Stefan-Boltzman)  máx · T = 2,897 · 10 -3 mK LEY DE STEFAN-BOLTZMAN LEY DEL DESPLAZAMIENTO DE WIEN LEYES EXPERIMENTALES

6. Hipótesis de Planck: cuantización de la energía La luz es emitida por la materia en cantidades discretas e indivisibles llamadas cuantos cuya energía es proporcional a la frecuencia  de la radiación emitida E = h ·  h = 6,624 · 10 -34 J s (Cte de Planck) Ley de Distribución de Planck ( explica el espectro de emisión térmica) Max Planck, 1900

7. Estudio experimental del Efecto Fotoeléctrico

8. Interpretación de Einstein Efecto Fotoeléctrico La radiación no sólo se emite de forma discreta, sino que se propaga y es absorbida de la misma manera. La luz está formada por paquetes de energía o fotones de energía h ·  Cuando un fotón incide sobre un metal si tiene suficiente energía h ·  0 ( Energía de extracción ) arrancará un electrón del mismo. Albert Einstein, Max Planck

9. Ecuación de Einstein del Efecto Fotoeléctrico FUNCIÓN DE EXTRACCIÓN W L = h ·  0 ECUACIÓN DE EINSTEIN DEL EFECTO FOTOELÉTRICO E c , máx = h  - W L = h  - h  0

10. Espectros Emisión Espectro continuo Espectro discontinuo Sólidos, estrellas (bolas de plasma) Átomos

11. Modelo Atómico de Bohr: Antecedentes Átomo de Rutherford Problemas Átomo inestable No explica espectros discontinuos

12. Modelo Atómico de Bohr: Postulados Neils Bohr, 1913 El e - gira alrededor del núcleo sólo en determinadas órbitas , estados estacionarios, en ellas ni se pierde, ni se absorbe energía. F centrípeta = F electrostática Sólo son posibles determinadas órbitas, aquellas que son un múltiplo entero del momento angular del e - . L = m · r · v = n · n (número cuántico) = (1,2,3 …) La energía liberada al caer el electrón desde una órbita a otra de menor energía se emite en forma de fotón, cuya frecuencia viene dada por la ecuación de Planck: E a - E b = h · v

13. Modelo Atómico de Borh: Transiciones Electrónicas

14. Modelo de Bohr: Espectro del Hidrógeno

15. Espectro del Hidrógeno J. Rydberg R H = 1,097 · 10 7 m -1 (Cte de Rydberg del hidrógeno) m y n son números enteros tales que n > m . – = R H ·

16. Hipótesis de De Broglie: dualidad onda-corpúsculo Si las ondas de la luz pueden comportarse como partícula ¿los electrones pueden ser ondas? Louis De Broglie, 1924

17. Hipótesis de De Broglie: dualidad onda-partícula Partículas Ondas Energía, E E = m · c 2 Momento, p p = m · v Frecuencia, f f = c /  Longitud de Onda,  E = h · f m · c 2 = h · c /  m · c = h /   m · v = h /  p = h /  Onda-Partícula