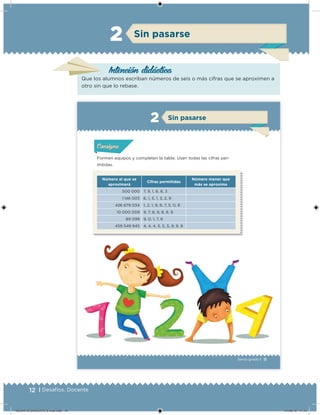
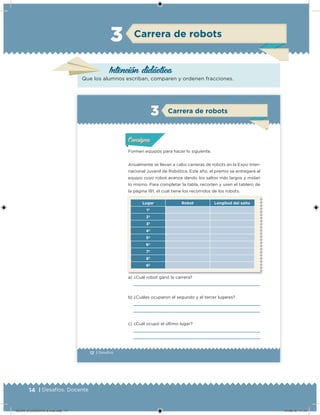
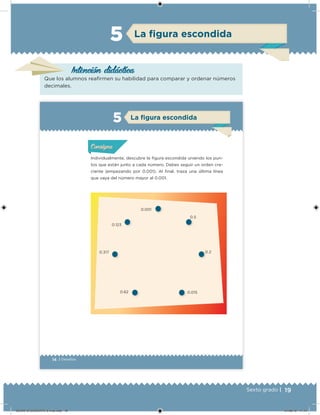
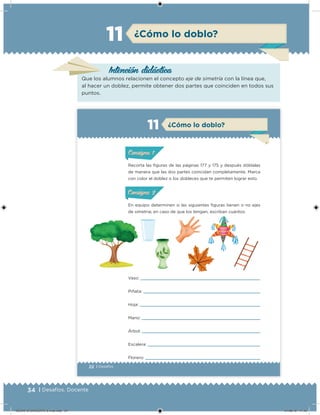
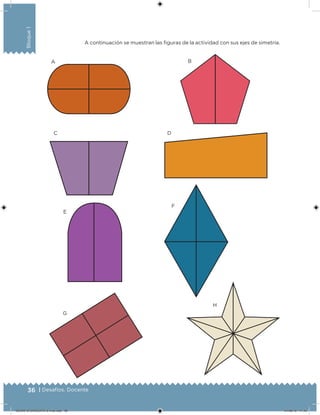
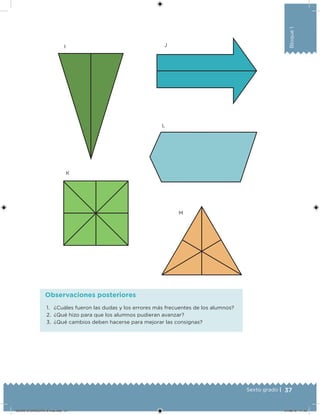
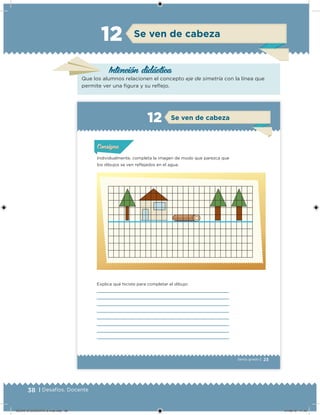
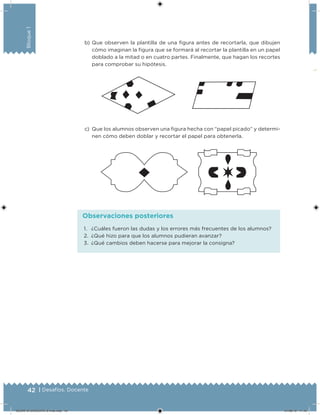
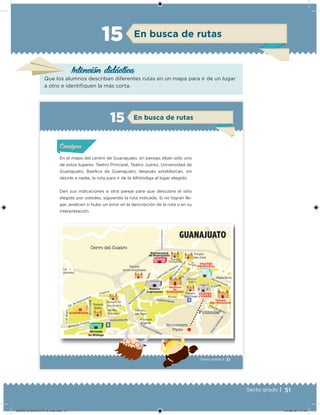
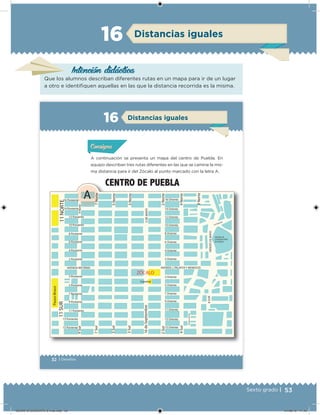
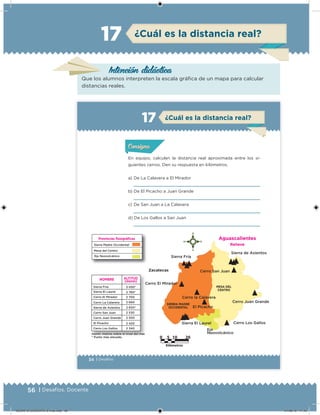
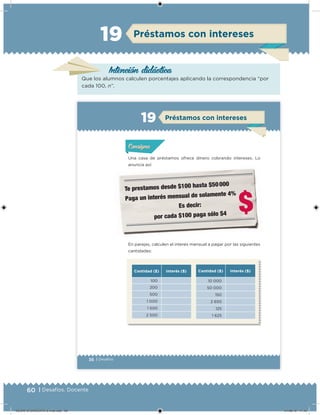
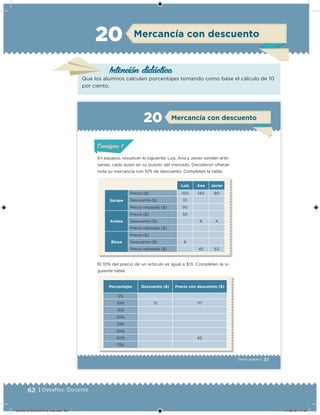
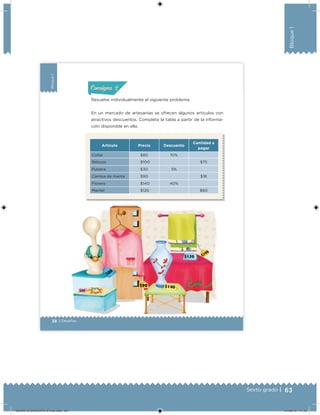
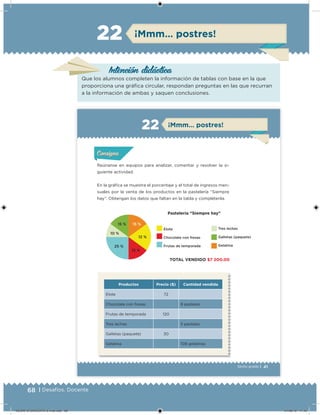
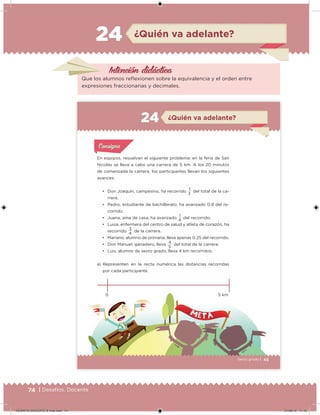
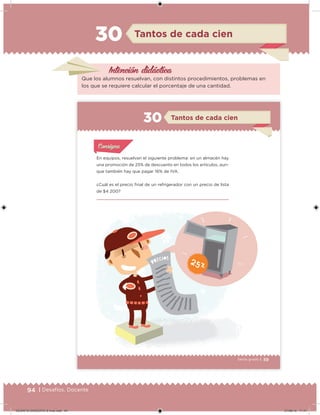
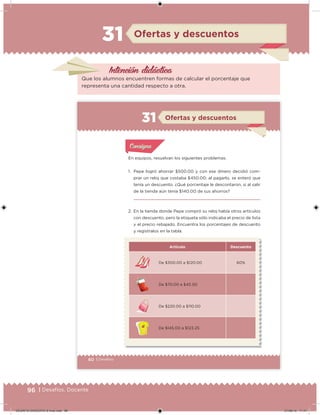
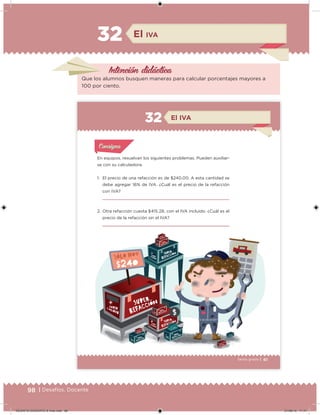
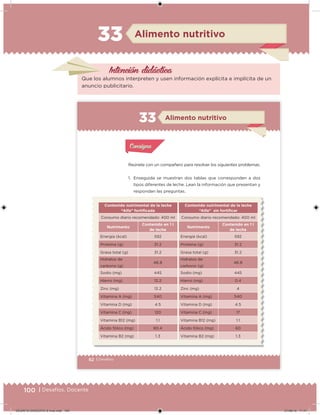
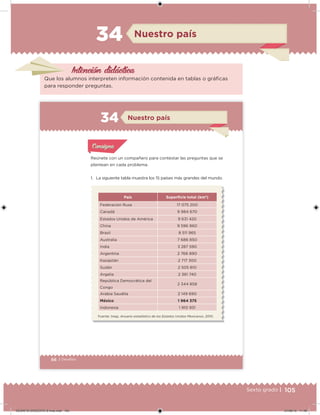
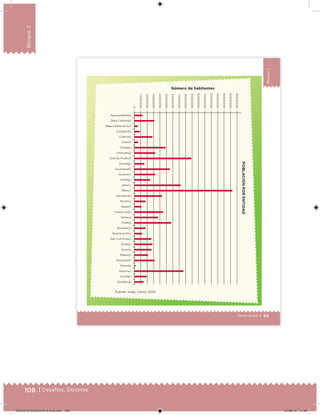
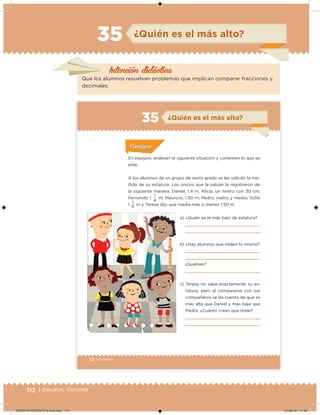
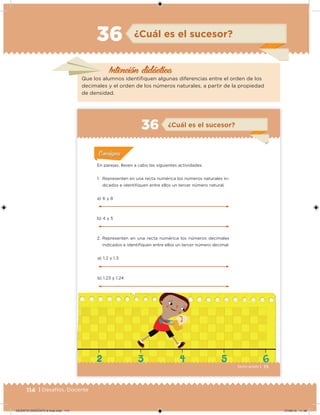
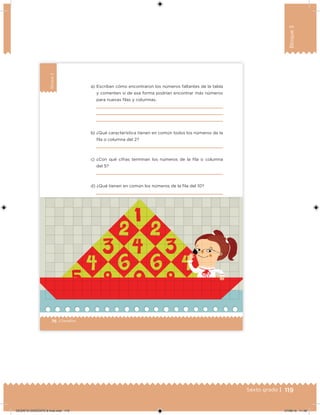
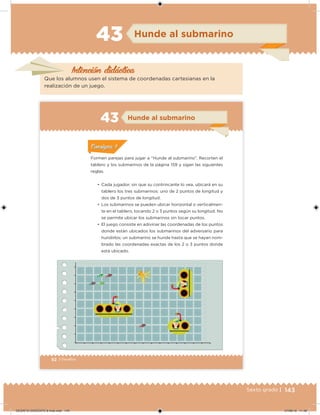
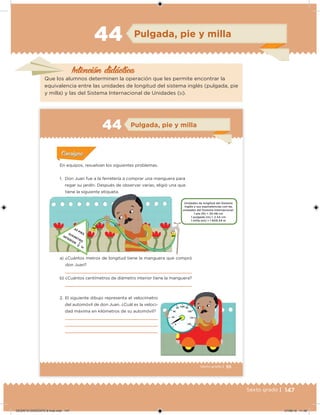
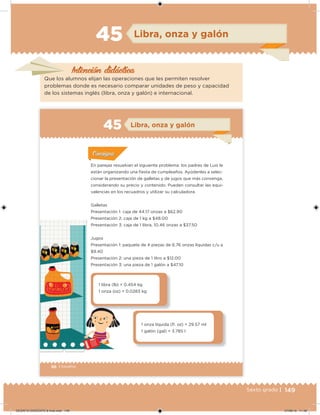
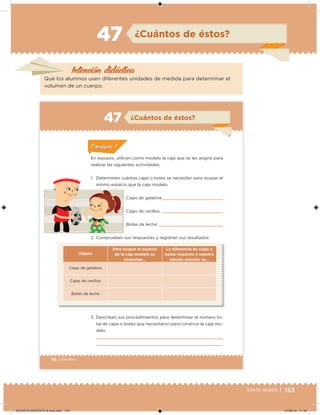
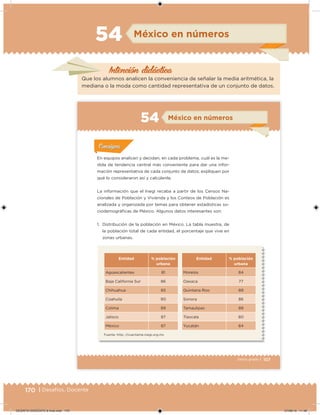
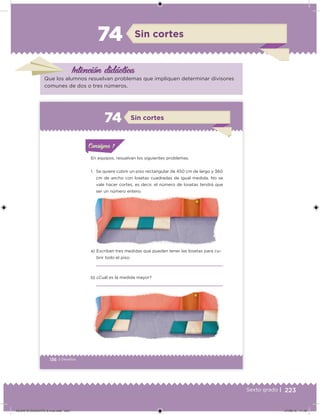
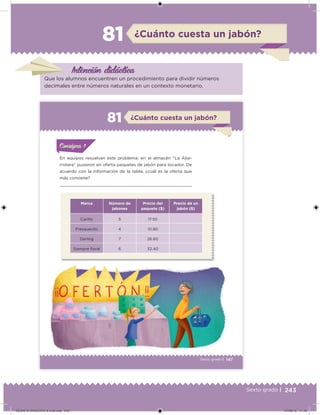
Este documento presenta un libro de texto para el sexto grado de educación primaria en México. Explica que el libro fue desarrollado por funcionarios del gobierno mexicano para apoyar la educación gratuita. Incluye una lista de los funcionarios que trabajaron en el proyecto y describe brevemente el contenido del libro de texto, el cual cubre temas como matemáticas, ciencias sociales y lenguaje. Finalmente, enfatiza la importancia de los libros de texto gratuitos para garantizar el derecho a la educación de todos