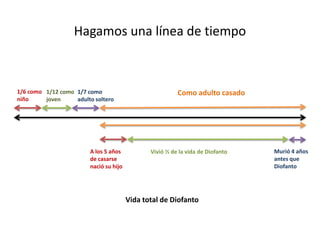
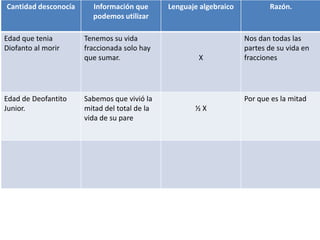
Diofanto vivió 1/6 de su vida como niño, 1/12 como joven, y 1/7 como adulto soltero. Se casó al final de esas etapas y tuvo un hijo 5 años después. Su hijo murió 4 años antes que él, y Diofanto vivió el doble que su hijo. Para calcular la edad de Diofanto al morir, se convierten las fracciones a números enteros usando un mínimo común múltiplo y se suman.

1. Resolución de problema
La leyenda de la lapida de Diofanto.
Explicado por el alumno Hugo Cesar Barrera J.
Estudiante de la universidad UTT en la carrera
Procesos Industriales, 1° A.
Profesor Lic. Edgar Mata

2. Esta es una antigua leyenda que se supone estuvo en
la lapida de Diofanto. Diofanto vivió 1/6 de su vida
como niño, 1/12 parte de su vida como joven y 1/7
como adulto soltero. Su hijo nació 5 años después de
su matrimonio de Diofanto pero murió 4 años mas
que su padre. Diofanto vivió el doble de su hijo.
¿calcule la edad de Diofanto al morir?

3. Una vez leído el problema, lo que debemos hacer es
detectar la información importante. Que es este caso
seria:
¿Qué edad tenia Diofanto al morir?
• Vivió 1/6 de su vida como niño.
• Vivió 1/12 de su vida como joven
• Vivió 1/7 de su vida como adulto soltero.
• Su hijo nació 5 años después de su matrimonio
• Murió 4 años antes que Diofanto
• Diofanto vivió el doble que su hijo.

4. Una vez seleccionada la información tal vez creerás
que falta información ya que no menciona en que
parte de su vida Diofanto se caso.
Si piensas esto quiere decir que no has analizado bien
la información que se nos da.
La respuesta a la fecha en que se caso es el resto de
su vida después de vivir como niño, joven y adulto
soltero. Revisemos una parte.
Dice Diofanto vivió 1/6 de su vida como niño.
Esto quiere decir que ese tiempo ya lo vivió y ocupo
1/6 de su vida en el pero ahí termino.
¿No te queda muy claro?......

5. Hagamos una línea de tiempo
1/6 como 1/12 como 1/7 como Como adulto casado
niño joven adulto soltero
A los 5 años Vivió ½ de la vida de Diofanto Murió 4 años
de casarse antes que
nació su hijo Diofanto
Vida total de Diofanto

6. Cantidad desconocía Información que Lenguaje algebraico Razón.
podemos utilizar
Edad que tenia Tenemos su vida Nos dan todas las
Diofanto al morir fraccionada solo hay partes de su vida en
que sumar. X fracciones
Edad de Deofantito Sabemos que vivió la Por que es la mitad
Junior. mitad del total de la ½X
vida de su pare

7. Ahora resolveremos el problema. Para poder convertir
las fracciones a numero enteros.
X = 1/6 + 1/12 + 1/7 + 5 + ½ + 4
Como ya tenemos dos numero enteros no hay que
meterlos en la suma de fracciones. Entonces los
sumaremos y los pasaremos con la X y queda así.
-9+X = 1/6 + 1/12 + 1/7 + ½
Busquemos un mínimo común múltiplo
En este caso seria 84
Y nos quedaría así
-9+X = 14/84 + 7/84 + 12/84 + 42/84