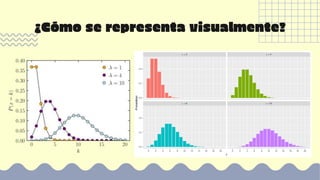
La distribución de Poisson es una distribución de probabilidad discreta ampliamente utilizada en biología y medicina para modelar el número de eventos aleatorios en un intervalo. Se representa matemáticamente como f(x)=e^-λλx/x!, donde λ es el parámetro de la distribución y el número promedio de veces que ocurre el evento. Se usa cuando n es grande y el evento es poco frecuente.