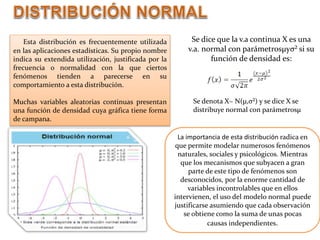
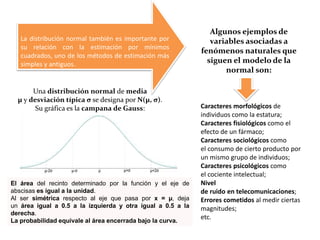
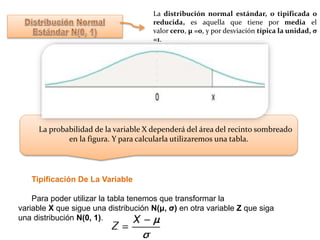
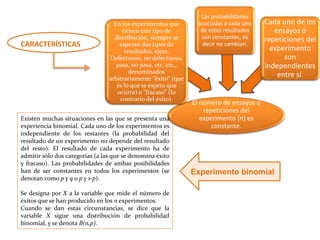
Este documento presenta información sobre diferentes distribuciones de probabilidad como la normal, binomial, de Poisson y sus características. Explica que la distribución normal es importante para modelar fenómenos naturales y que sigue la curva de Gauss. También describe las características de la distribución binomial como el número de ensayos n y la probabilidad de éxito p. Finalmente, indica que la distribución de Poisson se aplica cuando n es grande y p es pequeña en una distribución binomial.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR
PARA LA EDUCACIÓN UNIVERSITARIA
CIENCIA Y TECNOLOGÍA
INSTITUTO UNIVERSITARIO POLITÉCNICO
“SANTIAGO MARIÑO”
EXTENSIÓN BARINAS
Autor: Ing. Ronal Torres
C.I. 19.956.244.
Materia: Estadística II
Prof. Ing. Gilberto Linares
Barinas; Febrero 2017

2. Esta distribución es frecuentemente utilizada
en las aplicaciones estadísticas. Su propio nombre
indica su extendida utilización, justificada por la
frecuencia o normalidad con la que ciertos
fenómenos tienden a parecerse en su
comportamiento a esta distribución.
Muchas variables aleatorias continuas presentan
una función de densidad cuya gráfica tiene forma
de campana.
La importancia de esta distribución radica en
que permite modelar numerosos fenómenos
naturales, sociales y psicológicos. Mientras
que los mecanismos que subyacen a gran
parte de este tipo de fenómenos son
desconocidos, por la enorme cantidad de
variables incontrolables que en ellos
intervienen, el uso del modelo normal puede
justificarse asumiendo que cada observación
se obtiene como la suma de unas pocas
causas independientes.
Se dice que la v.a continua X es una
v.a. normal con parámetrosµyσ² si su
función de densidad es:
Se denota X~ N(µ,σ²) y se dice X se
distribuye normal con parámetrosµ

3. Caracteres morfológicos de
individuos como la estatura;
Caracteres fisiológicos como el
efecto de un fármaco;
Caracteres sociológicos como
el consumo de cierto producto por
un mismo grupo de individuos;
Caracteres psicológicos como
el cociente intelectual;
Nivel
de ruido en telecomunicaciones;
Errores cometidos al medir ciertas
magnitudes;
etc.
La distribución normal también es importante por
su relación con la estimación por mínimos
cuadrados, uno de los métodos de estimación más
simples y antiguos.
Algunos ejemplos de
variables asociadas a
fenómenos naturales que
siguen el modelo de la
normal son:
El área del recinto determinado por la función y el eje de
abscisas es igual a la unidad.
Al ser simétrica respecto al eje que pasa por x = µ, deja
un área igual a 0.5 a la izquierda y otra igual a 0.5 a la
derecha.
La probabilidad equivale al área encerrada bajo la curva.
Una distribución normal de media
μ y desviación típica σ se designa por N(μ, σ).
Su gráfica es la campana de Gauss:

4. La distribución normal estándar, o tipificada o
reducida, es aquella que tiene por media el
valor cero, μ =0, y por desviación típica la unidad, σ
=1.
La probabilidad de la variable X dependerá del área del recinto sombreado
en la figura. Y para calcularla utilizaremos una tabla.
Tipificación De La Variable
Para poder utilizar la tabla tenemos que transformar la
variable X que sigue una distribución N(μ, σ) en otra variable Z que siga
una distribución N(0, 1).

5. La distribución binomial es una distribución de
probabilidad discreta que mide el número de éxitos en
una secuencia de n ensayos de Bernoulli independientes
entre sí, con una probabilidad fija p de ocurrencia del
éxito entre los ensayos. Un experimento de Bernoulli se
caracteriza por ser dicotómico, esto es, sólo son posibles
dos resultados. A uno de estos se denomina éxito y tiene
una probabilidad de ocurrencia p y al otro, fracaso, con
una probabilidad q = 1 - p.
Para representar que
una variable
aleatoria X sigue una
distribución binomial
de parámetros n y p, se
escribe:
*La distribución binomial
es la base del test
binomial de significación
estadístican es el número de pruebas.
k es el número de éxitos.
p. es la probabilidad de éxito.
q es la probabilidad de fracaso.
El número combinatorio

6. CARACTERÍSTICAS
El número de ensayos o
repeticiones del
experimento (n) es
constante.
En los experimentos que
tienen este tipo de
distribución, siempre se
esperan dos tipos de
resultados, ejem.
Defectuoso, no defectuoso,
pasa, no pasa, etc, etc.,
denominados
arbitrariamente “éxito” (que
es lo que se espera que
ocurra) o “fracaso” (lo
contrario del éxito).
Las probabilidades
asociadas a cada uno
de estos resultados
son constantes, es
decir no cambian.
Cada uno de los
ensayos o
repeticiones del
experimento
son
independientes
entre sí.
Existen muchas situaciones en las que se presenta una
experiencia binomial. Cada uno de los experimentos es
independiente de los restantes (la probabilidad del
resultado de un experimento no depende del resultado
del resto). El resultado de cada experimento ha de
admitir sólo dos categorías (a las que se denomina éxito
y fracaso). Las probabilidades de ambas posibilidades
han de ser constantes en todos los experimentos (se
denotan como p y q o p y 1-p).
Se designa por X a la variable que mide el número de
éxitos que se han producido en los n experimentos.
Cuando se dan estas circunstancias, se dice que la
variable X sigue una distribución de probabilidad
binomial, y se denota B(n,p).
Experimento binomial

7. La distribución de Poisson parte de la distribución
binomial:
la distribución de Poisson es una distribución de
probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia
media, la probabilidad de que ocurra un determinado número de eventos
durante cierto período de tiempo. Concretamente, se especializa en la
probabilidad de ocurrencia de sucesos con probabilidades muy pequeñas,
o sucesos "raros".
•Fue descubierta por Simeón-Denis Poisson, que la dio a conocer
en 1838 en su trabajo Recherches sur la probabilité des jugements en
matières criminelles et matière civile (Investigación sobre la probabilidad
de los juicios en materias criminales y civiles).

8. Cuando en una distribución binomial se
realiza el experimento un número "n" muy
elevado de veces y la probabilidad de éxito "p"
en cada ensayo es reducida, entonces se aplica
el modelo de distribución de Poisson:
Se tiene que cumplir que: " p " < 0,10
" p * n " < 10
Para determinar la probabilidad de que
ocurran x éxitos por unidad de tiempo, área,
o producto, la fórmula a utilizar sería:
La distribución de Poisson sigue el siguiente modelo:
Dónde:
p(x, l) = probabilidad de que ocurran x éxitos, cuando el número promedio
de ocurrencia de ellos es l
l = media o promedio de éxitos por unidad de tiempo, área o producto
e = 2.718
x = variable que nos denota el número de éxitos que se desea que ocurra
Hay que hacer notar que en
esta distribución el número
de éxitos que ocurren por
unidad de tiempo, área o
producto es totalmente al
azar y que cada intervalo de
tiempo es independiente de
otro intervalo dado, así como
cada área es independiente
de otra área dada y cada
producto es independiente
de otro producto dado.

9. En este tipo de experimentos los éxitos buscados son
expresados por unidad de área, tiempo, pieza, etc, etc,:
- # de defectos de una tela por m2
- # de aviones que aterrizan en un aeropuerto por día, hora,
minuto, etc, etc.
- # de bacterias por cm2 de cultivo
- # de llamadas telefónicas a un conmutador por hora,
minuto, etc, etc.
- # de llegadas de embarcaciones a un puerto por día, mes,
etc, etc.
Características

10. 6.- Varios test de inteligencia dieron una puntuación que sigue una ley
normal con media 100 y desviación típica 15.
b) ¿Qué intervalo centrado en 100 contiene al 50% de la población?
a) Determinar el porcentaje de población que obtendría un coeficiente entre 95 y
110.

11. b) Determine la probabilidad de que al menos uno de los conductores controlados haya
cometido alguna de las dos infracciones.
6.- En unas pruebas de alcoholemia se ha observado que el 5% de los conductores controlados
dan positivo en la prueba y que el 10% de los conductores controlados no llevan aprovechado
el cinturón de seguridad. También se ha observado que las dos infracciones son
independientes.
Un guardia de tráfico para cinco conductores al azar. Si tenemos en cuenta que el número de
conductores es suficientemente importante como para estimar que la proporción de
infractores no varía al hacer la selección.
a) Determinar la probabilidad de que exactamente tres conductores hayan cometido alguna
de las dos infracciones.

12. Solución
Sea:
x el número de partículas en el área de un disco bajo estudio
n = 1cm2 el tamaño de la muestra
el de un disco bajo estudio = 100cm2.
Sabemos que el número promedio de partículas es 0.1 partículas x cm2
El promedio de defectos en la superficie total será:
1 cm2. 0.1 partículas/cm2
100cm2  l
Por lo tanto, el número medio de contaminación de partículas para 100cm2 es de:
l = (100 cm2·* 0.1 partículas/cm2)/1 cm2 = 10 partículas
Luego entonces La distribución de Poisson para la probabilidad de que ocurran 12 partículas en
el área de cada disco esta dada por la formula:
6.- La contaminación constituye un problema en la fabricación de discos de
almacenamiento óptico. El número de partícula de contaminación que ocurre en
un disco óptico tiene a distribución de poisson y el numero promedio de partículas
por centímetro cuadrado de superficie del disco es 0.1, el área de un disco bajo
estudio es 100 centímetro cuadrado. Encuentre la probabilidad de que ocurran 12
partículas en el área del disco bajo estudio.

13. Resultado:
La probabilidad de que existan doce partículas de contaminación en los discos ópticos es
de, P(x=12) = 0.09478033.
Calcula la probabilidad de que el disco esté limpio; es decir, que ocurran cero partículas en
su área.
Esta dado por:
Luego entonces la probabilidad de que no existan partículas de contaminación en los discos
ópticos es de P(x=0)= 0.0000453999