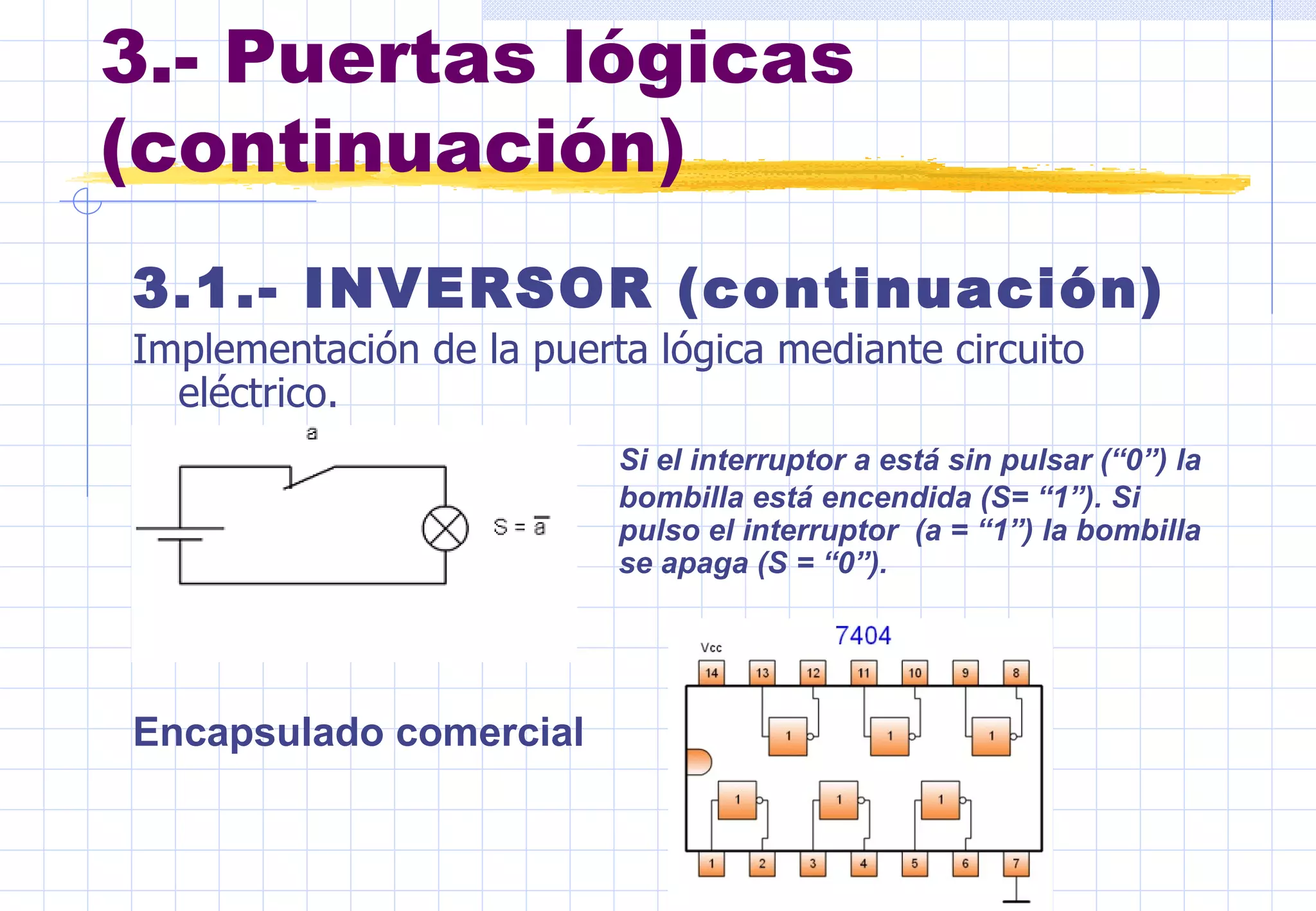
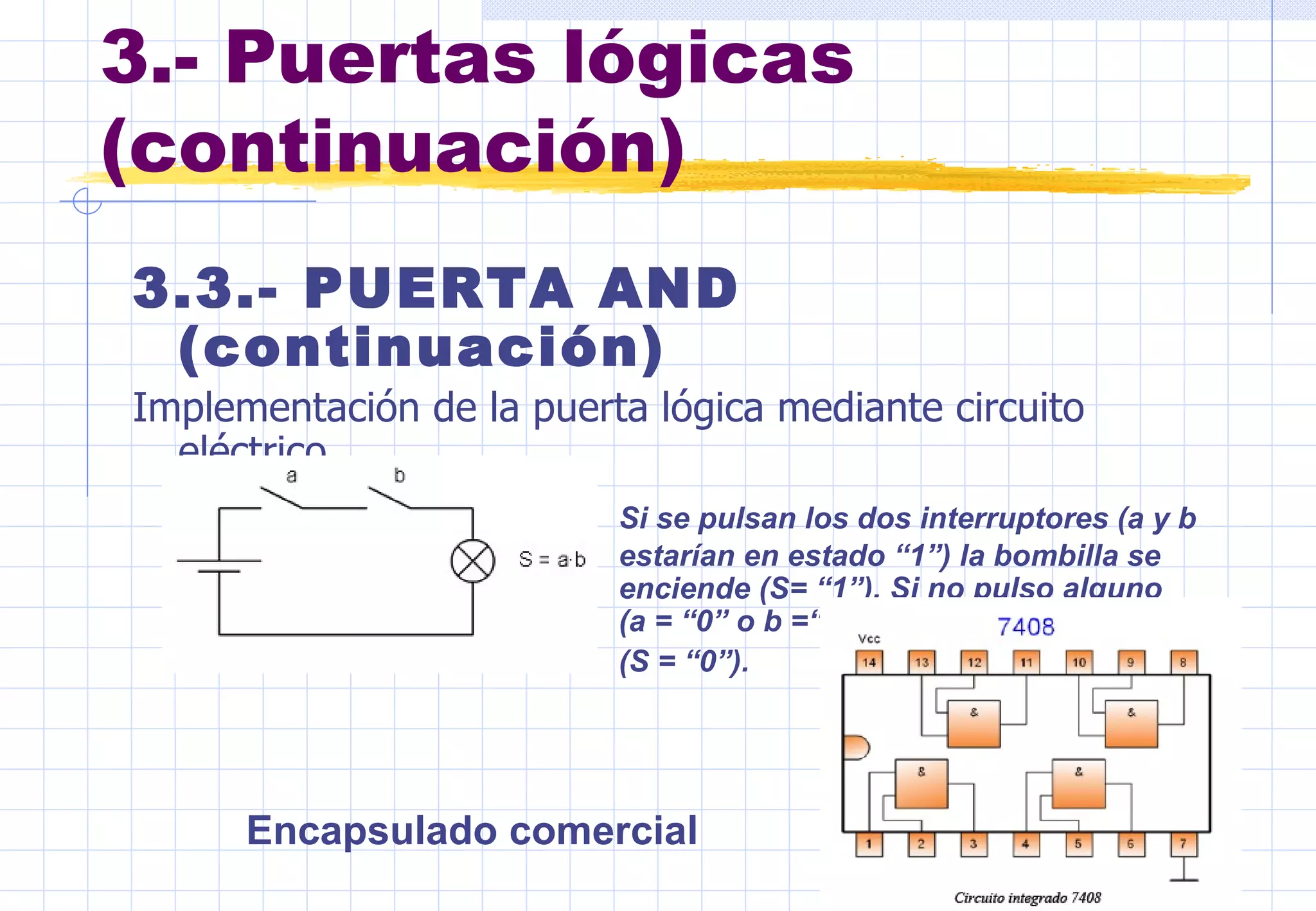
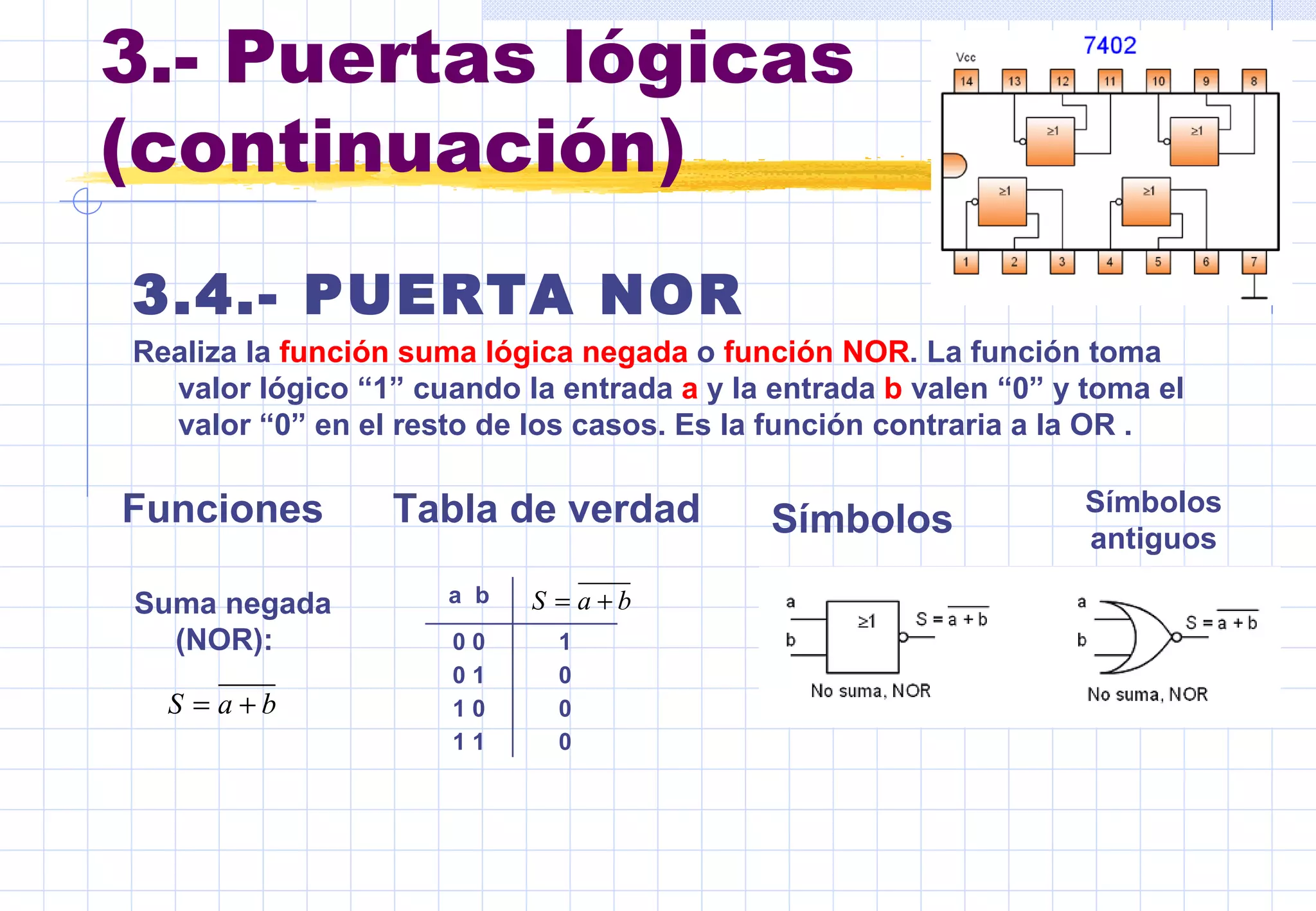
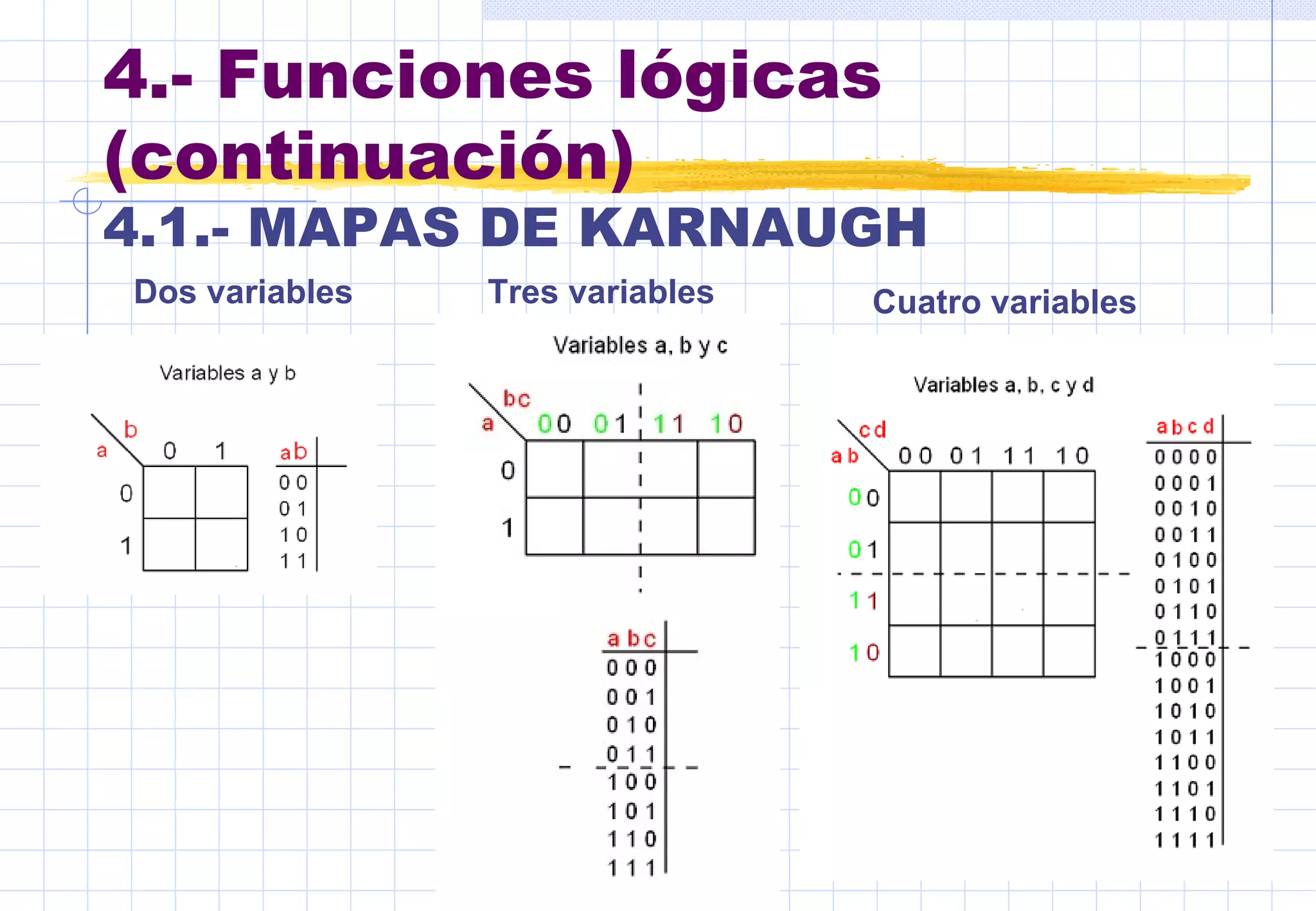
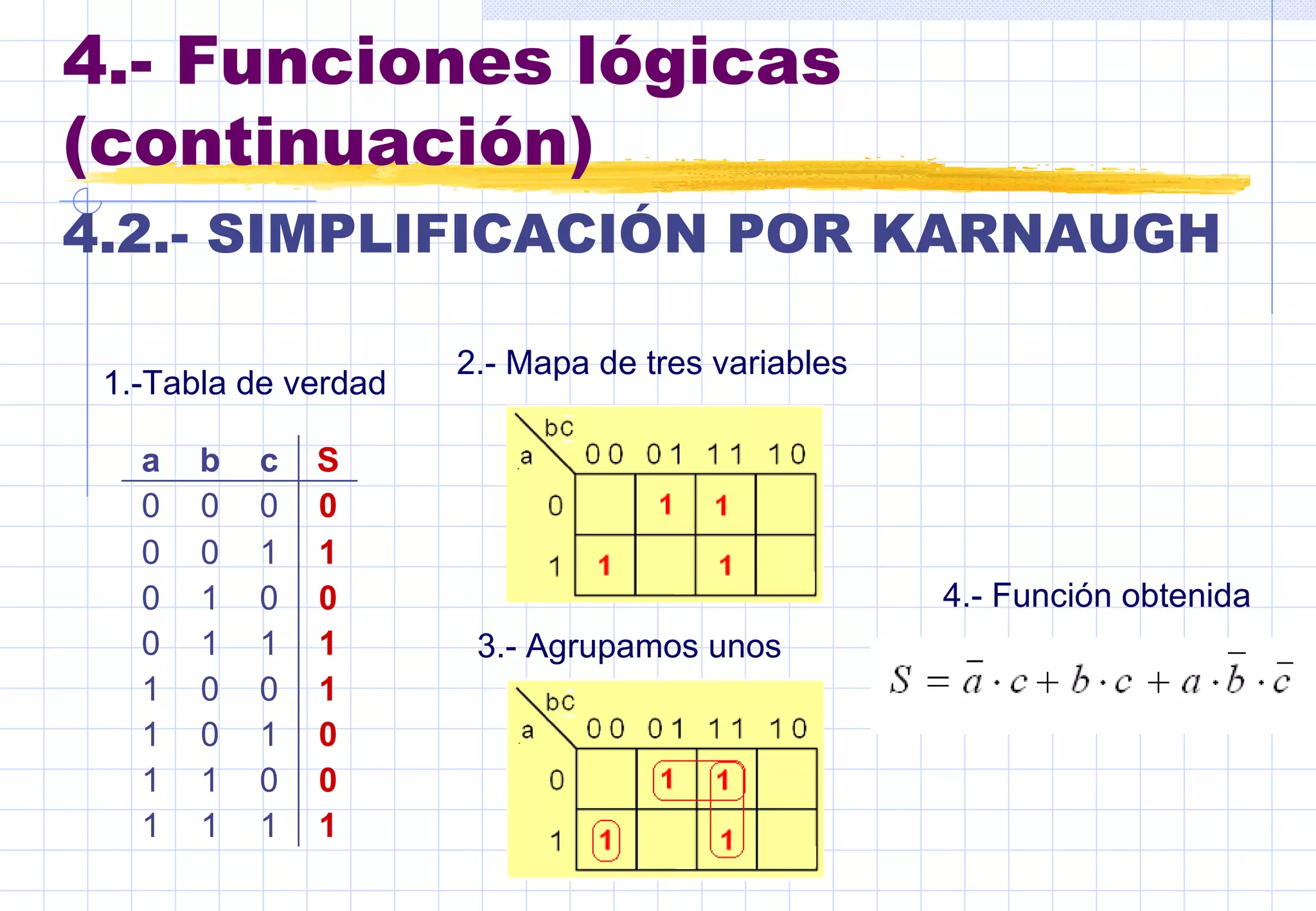
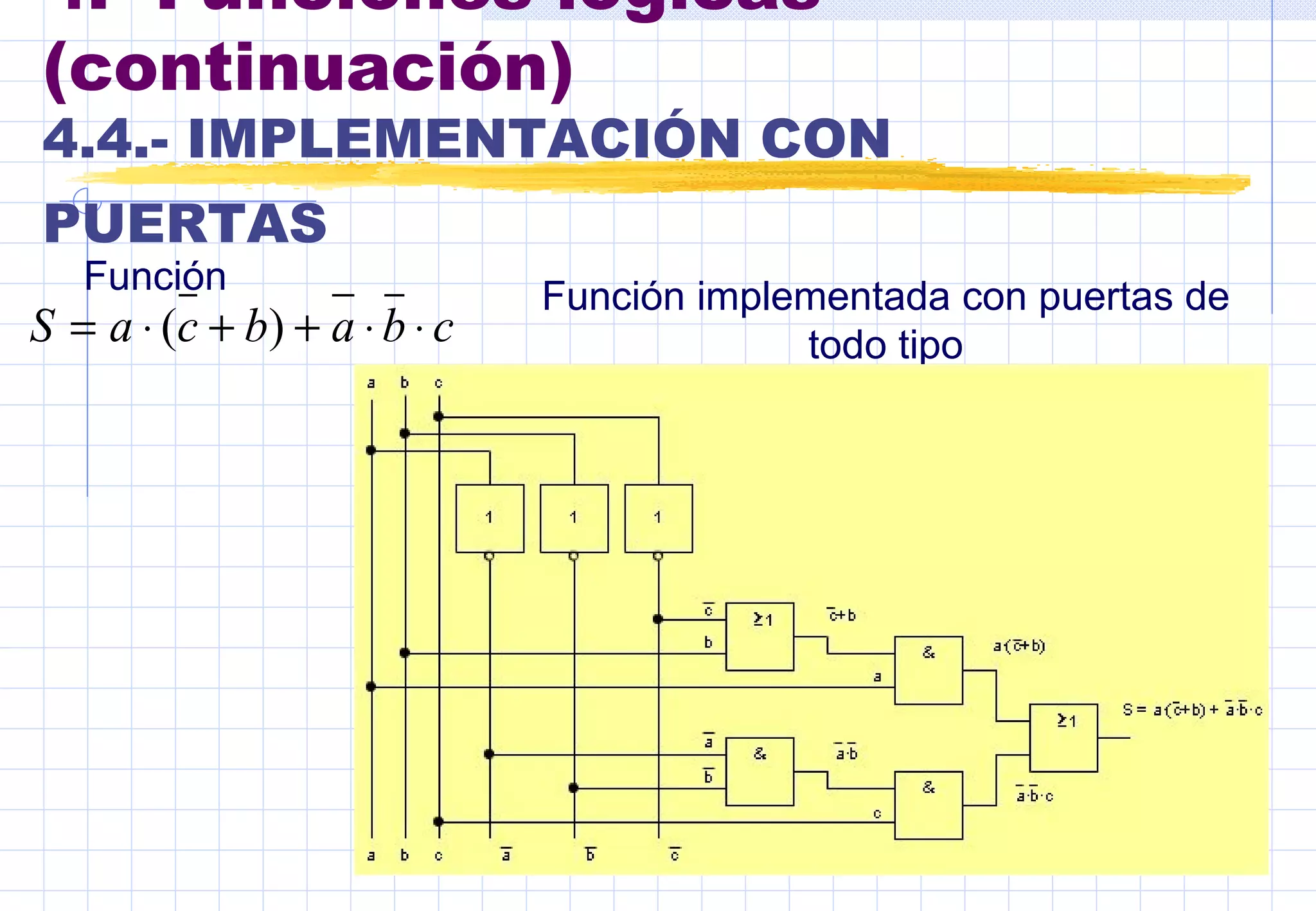
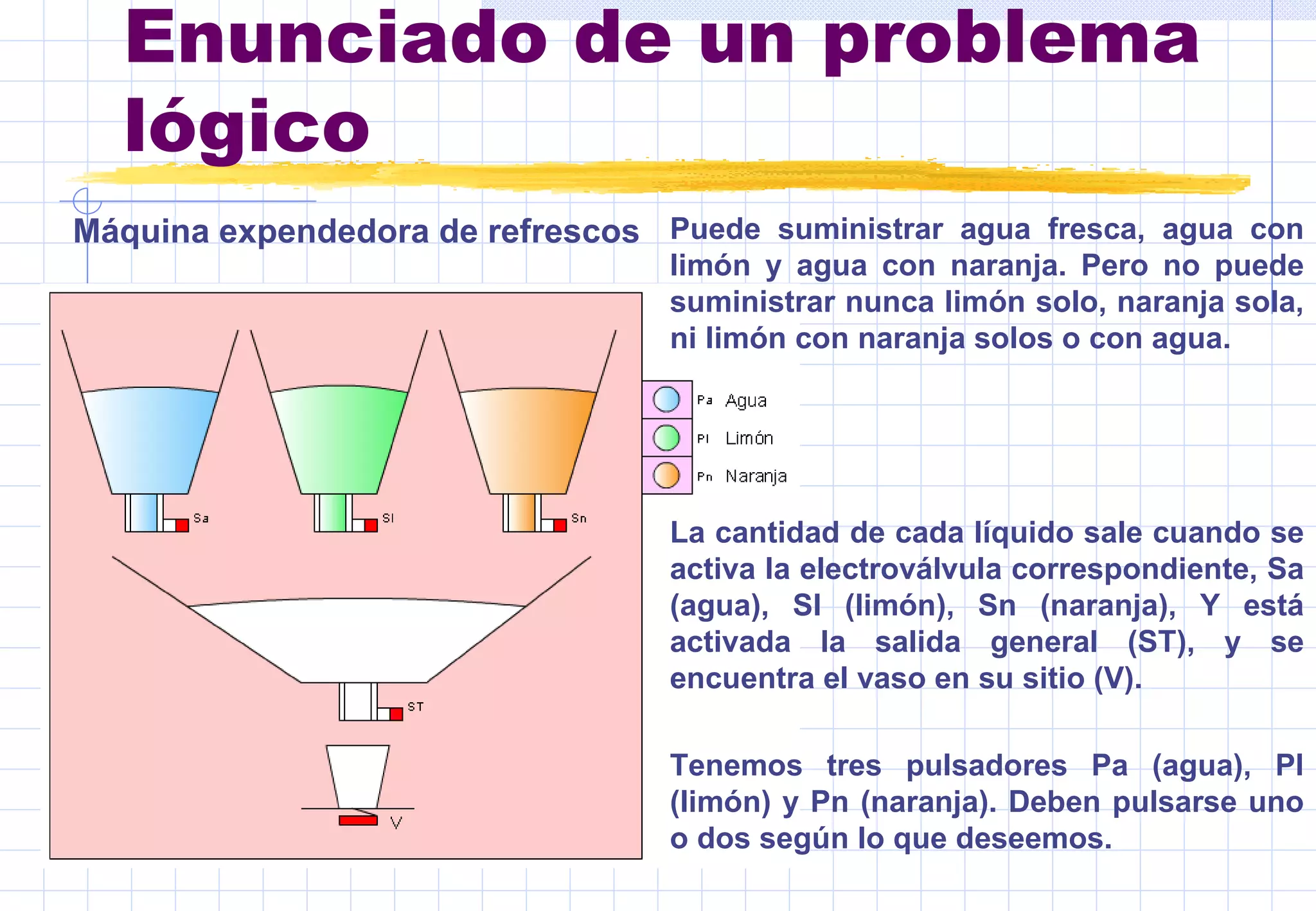
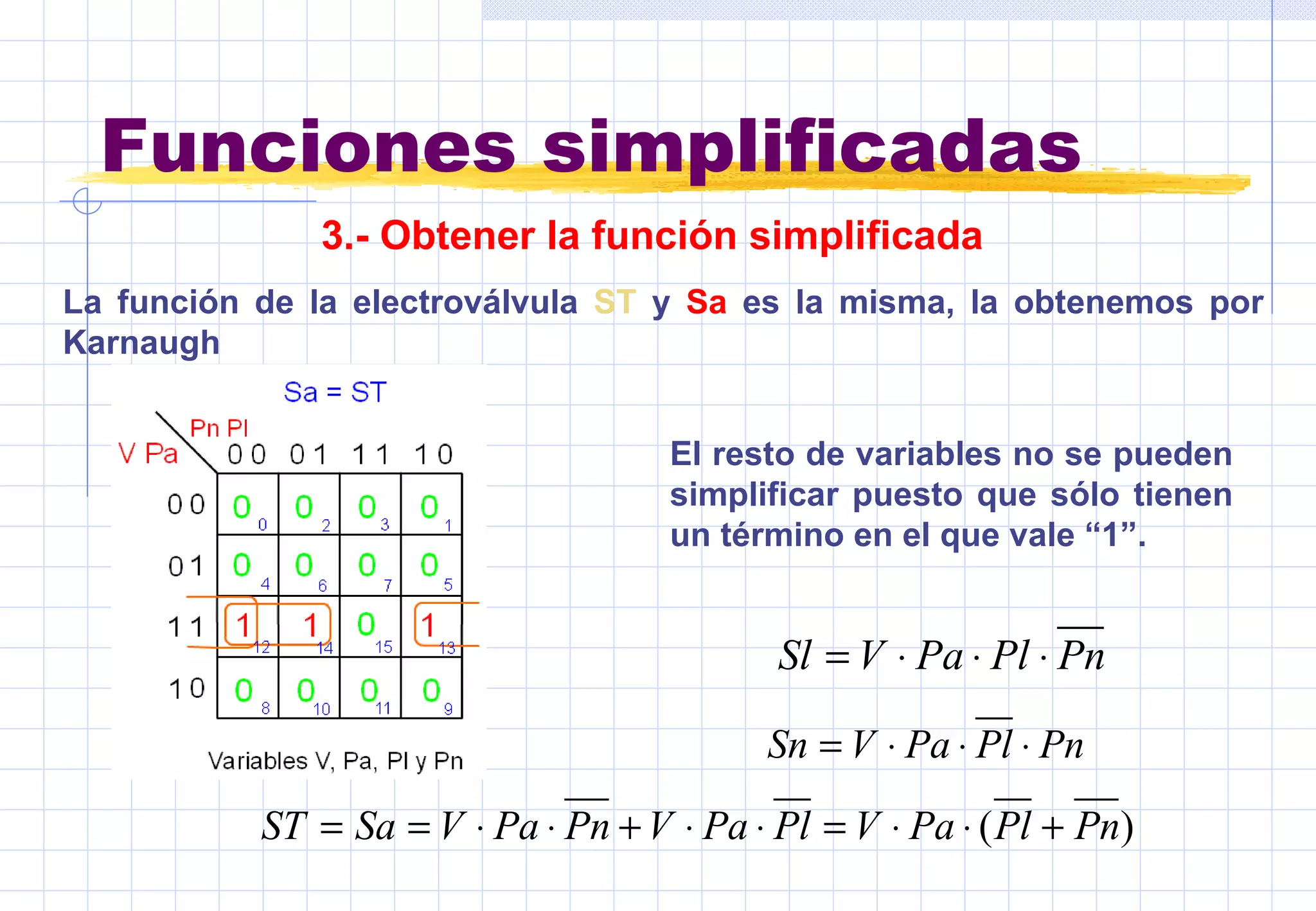
Este documento presenta conceptos básicos sobre sistemas digitales. Explica los sistemas de numeración binario y hexadecimal, y describe las funciones y tablas de verdad de puertas lógicas como inversor, OR, AND, NOR y NAND. También cubre mapas de Karnaug y simplificación de funciones lógicas mediante puertas.

1. Unidad Didáctica Electrónica Digital 4º ESO

2. ÍNDICE INTRODUCCIÓN SISTEMAS DE NUMERACIÓN PUERTAS LÓGICAS FUNCIONES LÓGICAS

3. 1.- Introducción Señal analógica. Señal digital Una señal analógica puede tener infinitos valores, positivos y/o negativos. La señal digital sólo puede tener dos valores 1 o 0. La gran ventaja es que la señal digital es más fiable en la transmisión de datos. En el ejemplo, la señal digital toma el valor 1 cuando supera al valor a , y toma valor 0 cuando desciende por debajo del valor b . Cuando la señal permanece entre los valores a y b , se mantiene con el valor anterior.

4. 2.- Sistemas de numeración 2.1.- Sistemas decimal. Se define la base de un sistema de numeración como el número de símbolos distintos que tiene. Normalmente trabajamos con el sistema decimal que tiene 10 dígitos: 0,1,2,3,4,5,6,7,8,9. Por ejemplo: a) El número 723,54 en base 10, lo podemos expresar: 723,54 = 7 x10 2 + 2 x10 1 + 3 x10 0 + 5 x10 -1 + 4 x10 -2

5. 2.- Sistemas de numeración (continuación) El número 11010,11 en base 2 es: Conversión de Binario a Decimal: 1 x2 4 + 1 x2 3 + 0 x2 2 + 1 x2 1 + 0 x2 0 + 1 x2 -1 + 1 x2 -2 = 16 + 8 + 0 + 2 + 0 + 0,5 + 0,25 = 26,75 El número 26,75 en base decimal Conversión de Decimal a Binario: El número 37 en base decimal es: 37 en base 10 = 100101 en base binaria 2.2.- Sistema binario. Consta de dos dígitos el 0 y el 1. A cada uno de ellos se le llama bit.

6. 2.- Sistemas de numeración (continuación) Equivalencia entre los sistemas Hexadecimal, Binario y Decimal 1111 15 F 111 0 14 E 11 0 1 13 D 11 00 12 C 1 0 11 11 B 1 0 1 0 10 A 1 00 1 9 9 1 000 8 8 0 111 7 7 0 11 0 6 6 0 1 0 1 5 5 0 1 00 4 4 00 11 3 3 00 1 0 2 2 000 1 1 1 0000 0 0 Binario D ecimal Hexadecimal

7. 3.- Puertas lógicas Las puertas lógicas son componentes electrónicos capaces de realizar las operaciones lógicas. A continuación se detallan las más importantes. 3.1.- INVERSOR Realiza la función negación lógica . La función toma valor lógico “1” cuando la entrada a vale “0” y toma el valor “0” cuando la entrada a vale “1”. También se la conoce como función Inversión . Negación (¯) : S = ā Tabla de verdad Símbolo Símbolos antiguos 0 1 1 0 S = ā a

8. 3.- Puertas lógicas (continuación) 3.1.- INVERSOR (continuación) Implementación de la puerta lógica mediante circuito eléctrico. Si el interruptor a está sin pulsar (“0”) la bombilla está encendida (S= “1”). Si pulso el interruptor (a = “1”) la bombilla se apaga (S = “0”). Encapsulado comercial

9. 3.- Puertas lógicas (continuación) 3.2.- PUERTA OR Realiza la función suma lógica o función OR . La función toma valor lógico “1” cuando la entrada a o la entrada b valen “1” y toma el valor “0” cuando las dos entradas valen “0”. Funciones Tabla de verdad Símbolos Símbolos antiguos Suma (OR): S = a + b 1 1 1 1 1 0 1 0 1 0 0 0 S = a+b a b

10. 3.- Puertas lógicas (continuación) 3.2.- PUERTA OR (continuación) Implementación de la puerta lógica mediante circuito eléctrico. Si se pulsa cualquier interruptor (a o b estarían en estado “1”) la bombilla se enciende (S= “1”). Si no pulso ninguno (a = “0” y b =“0”) la bombilla se apaga (S = “0”). Encapsulado comercial

11. 3.- Puertas lógicas (continuación) 3.3.- PUERTA AND Realiza la función producto lógico o función AND . La función toma valor lógico “1” cuando la entrada a y la entrada b valen “1” y toma el valor “0” cuando alguna de las dos entradas vale “0”. Funciones Tabla de verdad Símbolos Símbolos antiguos Multiplicación (AND): S = a · b 1 1 1 0 1 0 0 0 1 0 0 0 S = a·b a b

12. 3.- Puertas lógicas (continuación) 3.3.- PUERTA AND (continuación) Implementación de la puerta lógica mediante circuito eléctrico. Si se pulsan los dos interruptores (a y b estarían en estado “1”) la bombilla se enciende (S= “1”). Si no pulso alguno (a = “0” o b =“0”) la bombilla se apaga (S = “0”). Encapsulado comercial

13. 3.- Puertas lógicas (continuación) 3.4.- PUERTA NOR Realiza la función suma lógica negada o función NOR . La función toma valor lógico “1” cuando la entrada a y la entrada b valen “0” y toma el valor “0” en el resto de los casos. Es la función contraria a la OR . Funciones Tabla de verdad Símbolos Símbolos antiguos Suma negada (NOR): 0 1 1 0 1 0 0 0 1 1 0 0 a b

14. 3.- Puertas lógicas (continuación) 3.5.- PUERTA NAND Realiza la función producto lógico negado o función NAND . La función toma valor lógico “1” cuando la entrada a y la entrada b valen “0” y toma el valor “0” en el resto de los casos. Es la función contraria a la AND . Funciones Tabla de verdad Símbolos Símbolos antiguos Multiplicación negada (NAND): 0 1 1 1 1 0 1 0 1 1 0 0 a b

15. 3.- Puertas lógicas (continuación) 3.6.- PUERTA OR EXCLUSIVA Realiza la función OR EXCLUSIVA . La función toma valor lógico “1” cuando las entradas a y b tienen distinto valor y toma el valor “0” cuando las entradas a y b son iguales. Funciones Tabla de verdad Símbolos Símbolos antiguos OR exclusiva (EXOR) : 0 1 1 1 1 0 1 0 1 0 0 0 a b

16. 4.- Funciones lógicas Función lógica Tabla de verdad Por Minterms La función se puede obtener de dos formas, como suma de productos ( Minterms ) o como producto de sumas ( Maxterms ). Por Maxterms 1 1 1 1 1 0 1 1 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 0 0 0 0 0 0 S c b a

17. 4.- Funciones lógicas (continuación) 4.1.- MAPAS DE KARNAUGH Dos variables Tres variables Cuatro variables

18. 4.- Funciones lógicas (continuación) 4.2.- SIMPLIFICACIÓN POR KARNAUGH 1.-Tabla de verdad 2.- Mapa de tres variables 3.- Agrupamos unos 4.- Función obtenida 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 0 0 0 0 0 0 S c b a

19. 4.- Funciones lógicas (continuación) 4.3.- IMPLEMENTACIÓN CON PUERTAS Función Función implementada con puertas de todo tipo

20. 4.- Funciones lógicas (continuación) 4.4.- IMPLEMENTACIÓN CON PUERTAS Función Función implementada con puertas de todo tipo

21. Resolución de problemas Pasos a seguir: 1.- Identificar las entradas y salidas 2.- Crear la tabla de verdad 3.- Obtener la función simplificada 4.- Implementar la función con puertas de todo tipo, puertas NAND y puertas NOR

22. Enunciado de un problema lógico Para poner en marcha un motor se requiere tres interruptores (a, b y c) de tal forma que el funcionamiento del mismo se produzca únicamente en las siguientes condiciones: • Cuando esté cerrado solamente b. • Cuando estén cerrados simultáneamente a y b y no lo esté c. • Cuando estén cerrados simultáneamente a y c y no lo esté b. Crea la tabla de verdad que represente el funcionamiento del circuito de control. Obtén la función expresada como suma de productos (Minterms). Obtén la expresión simplificada por Karnaugh de la función. Implementa la función utilizando puertas lógicas de todo tipo.

23. Identificar entradas y salidas 1.- Identificar las entradas y salidas Entradas : serán los interruptores a, b y c . Interruptor pulsado será “1” y no pulsado será “0” Salida: será el motor que está gobernado por los interruptores. C uando la salida de la función valga “1” indicará que en ese caso el motor funciona.

24. Tabla de verdad 2.- Crear la tabla de verdad

25. Funciones simplificadas 3.- Obtener la función simplificada La función del motor M la obtenemos por Karnaugh

26. Puertas de todo tipo 4.- Implementar la funci ó n con puertas de todo tipo

27. Enunciado de un problema lógico M áquina expendedora de refrescos P uede suministrar agua fresca, agua con limón y agua con naranja. Pero no puede suministrar nunca limón solo, naranja sola, ni limón con naranja solos o con agua. La cantidad de cada líquido sale cuando se activa la electroválvula correspondiente, Sa (agua), Sl (limón), Sn (naranja) , Y está activada la salida general (ST), y se encuentra el vaso en su sitio (V). T enemos tres pulsadores Pa (agua), Pl (limón) y Pn (naranja). Deben pulsarse uno o dos según lo que deseemos .

28. Identificar entradas y salidas 1.- Identificar las entradas y salidas Entradas , serán los pulsadores Pa, Pl, Pn y el sensor que detecta la presencia del vaso V . P ulsador pulsado será “1” y no pulsado será “0” Salidas , serán todas las electroválvulas sobre las que hay que actuar, Sa, Sl, Sn y ST . C uando la electroválvula en cuestión valga “1” permitirá que salga la cantidad de líquido necesario

29. Tabla de verdad 2.- Crear la tabla de verdad Entradas Salidas V Pa Pl Pn ST Sa Sl Sn 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 1 1 0 0 1 1 0 0 1 1 0 1 1 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 0 0 0 0

30. Funciones simplificadas La función de la electroválvula ST y Sa es la misma, la obtenemos por Karnaugh El resto de variables no se pueden simplificar puesto que sólo tienen un término en el que vale “1”. 3.- Obtener la función simplificada

31. Puertas de todo tipo 4.- Implementar la s funci o n es con puertas de todo tipo

32. Puertas NAND 4.- Implementar la s funci o n es con puertas NAND

33. Puertas NOR 4.- Implementar la s funci o n es con puertas NOR