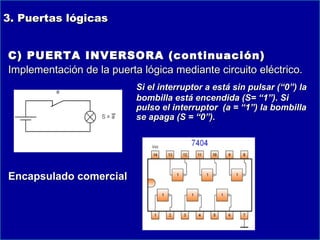
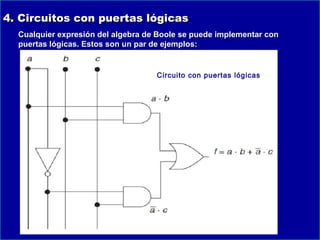
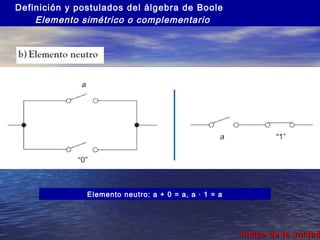
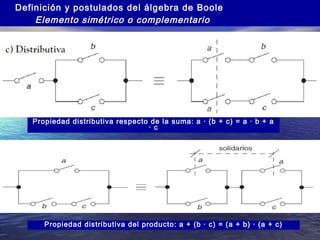
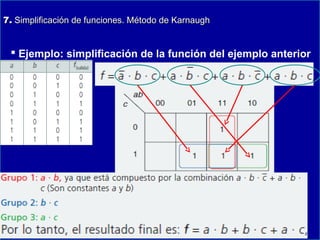
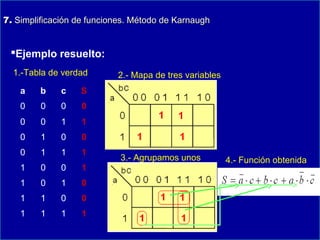
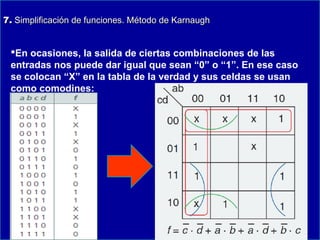
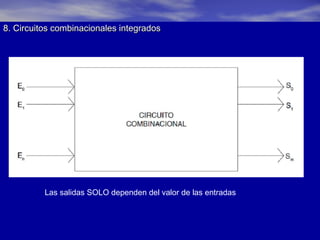
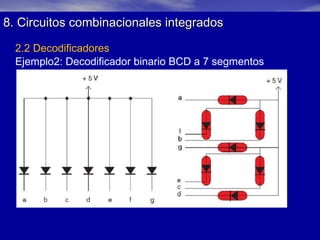
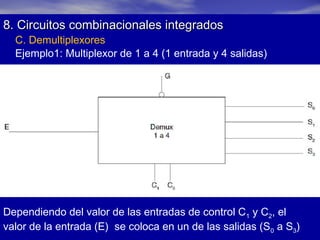
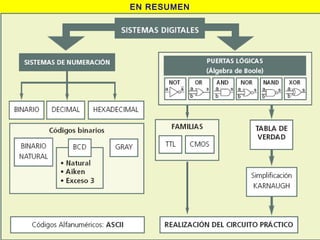
Este documento presenta información sobre lógica digital y circuitos combinacionales. Explica los sistemas de numeración binario, hexadecimal y BCD. Luego introduce el álgebra de Boole, incluyendo tablas de verdad y definiciones de puertas lógicas como AND, OR, NOT. También cubre temas como obtener funciones lógicas a partir de tablas de verdad, resolver problemas con puertas lógicas y simplificar funciones usando mapas de Karnaugh.

1. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES.
ALGEBRA DE BOOLE
INTRODUCCIÓN: Sistemas digitales y sistemas
analógicos
1 Sistemas de numeración y códigos
2 Álgebra de Boole. Definiciones
3 Puertas lógicas
4 Circuitos realizados con puertas lógicas
5 Obtener función a partir de tabla de verdad
6 Resolución de problemas con puertas lógicas
7 Simplificación de funciones: Karnaugh
8 CI Digitales

2. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
INTRODUCCIÓN:
Sistemas digitales y sistemas analógicos
• Una señal analógica puede tener infinitos valores, positivos
y/o negativos.
• La señal digital sólo puede tener dos valores 1 ó 0.
• La gran ventaja es que la señal
digital es más fiable en la
transmisión de datos.
• En el ejemplo, la señal digital
toma el valor 1 cuando supera
al valor a, y toma valor 0 cuando
desciende por debajo del valor b.
Cuando la señal permanece entre
los valores a y b, se mantiene
con el valor anterior.

3. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
Sistemas digitales y sistemas analógicos
•La electrónica se diferencia en analógica y digital
•La diferencia está en las señales con las que trabajan:
Puede tomar infinitos valores distintos
SEÑAL ANALÓGICA
Puede tomar sólo 2 valores distintos
En este curso hablaremos de “0” y “1”
SEÑAL DIGITAL

4. Sistemas digitales y sistemas analógicos
Figura 1.1.
Figura 1.2.
Señal analógica
Señal digital

5. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
1. Sistemas de numeración y códigos
 A lo largo de la historia se han usado muchos sistemas de
numeración. Actualmente utilizamos el Sistema Decimal
A.Sistemas de numeración
Se define la base de un sistema de numeración como el
número de símbolos distintos que tiene.
Normalmente trabajamos con el sistema decimal que tiene 10
dígitos: 0,1,2,3,4,5,6,7,8,9.
Por ejemplo:
El número 723,54 en base 10, lo podemos expresar:
723,54 = 7x102 + 2x101 + 3x100 + 5x10-1 + 4x10-2

6. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
B. Sistema binario.
Consta de dos dígitos el 0 y el 1. A cada uno de ellos se le llama bit.
Conversión de Binario a Decimal:
El número 11010 en base 2 es:
1x24 +1x23 + 0x22 + 1x21 + 0x20 = 16 + 8 + 0 + 2 + 0 + 0,5 + 0,25 =
Conversión de Decimal a
Binario:
El número 37 en base decimal es:
37 en base 10 = 100101 en base binaria
26,75

7. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
C. Sistema Hexadecimal
El sistema hexadecimal es el sistema de numeración de
base 16, empleando por tanto 16 símbolos:
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Para pasar de decimal a hexadecimal EJEMPLO:
5338 |_16
153 333|_16
158 013 20|_16
Para pasar de hexadecimal a decimal:
14DA
10
13 4 1 -> (5338)10 = (14DA16)
14DA16 = 10 ⋅16 0 + 13 ⋅161 + 4 ⋅16 2 + 1 ⋅16 3
Ver sistema octal (tabla 12.3 de p317)

8. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
Equivalencia entre los
sistemas Hexadecimal,
Binario y Decimal
VER TAMBIEN OCTAL!!!
Hexadecimal Decimal
0
0
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
A
10
B
11
C
12
D
13
E
14
F
15
Binario
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111

9. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
D. Códigos binarios
Hemos visto el código binario natural pero existen otros
códigos construidos a partir del 0 y el 1.
Ejemplo: Código Gray
De un número a otro sólo difieren en un bit. Es muy utilizado
por este motivo

10. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
Códigos BCD
Son códigos binarios que sólo tienen 10 combinaciones, del 0 al
9. Hay distintos tipos mostrados en la tabla:

11. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
Códigos BCD

12. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
2 Álgebra de Boole.
Se trata de las operaciones que se pueden hacer con la lógica
combinacional. Los valores sólo pueden ser lógicos (0 ó 1). Dependiendo
de los valores de entrada, el algebra de Boole nos permite conocer las
salidas.
Bit: Binary Digit
–0ó1
– Abierto ó Cerrado
– Bajo ó Alto
– Apagado ó Encendido
_ Verdadero o Falso
_ Conectado o desconectado

13. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
• Se pueden activar las entradas y las salidas de 2 formas:
 Activación a nivel bajo (lógica negativa):
Una entrada se activa a nivel bajo (0) cuando se le aplica un nivel bajo
de tensión (0 Voltios) y el circuito reconoce que dicha entrada está
activada
 Activación a nivel alto(lógica positiva):
Una entrada se activa a nivel alto (1) cuando se le aplica un nivel alto de
tensión (5 Voltios) y el circuito reconoce que dicha entrada está activada

14. LOGICA DIGITAL
CIRCUITOS COMBINACIONALES
•¿Qué es la tabla de la verdad de una función lógica?
Muestra todas las combinaciones posibles de las variables de
entrada (en binario) con sus correspondientes resultados
(variables de salida)
Ejemplo de tabla de verdad para la función f
(salida) que depende de 3 entradas (a,b,c)
• ¿Qué son las puertas lógicas?
Las puertas lógicas son componentes electrónicos capaces de
realizar las operaciones lógicas del álgebra de Boole. Se encuentran
dentro de circuitos integrados.

15. 3. Puertas lógicas
A) PUERTA OR
Realiza la función suma lógica o función OR. La
función toma valor lógico “1” cuando la entrada a o
la entrada b valen “1” y toma el valor “0” cuando las
dos entradas valen “0”.
Tabla de verdad y símbolo de la puerta OR

16. 3. Puertas lógicas
A) PUERTA OR (continuación)
Implementación de la puerta lógica mediante circuito
eléctrico.
Si se pulsa cualquier interruptor
(a o b estarían en estado “1”) la
bombilla se enciende (S= “1”). Si
no pulso ninguno (a=“0” y b=“0”)
la bombilla se apaga (S = “0”).
Encapsulado comercial

17. 3. Puertas lógicas
B) PUERTA AND
Realiza la función producto lógico o función AND. La
función toma valor lógico “1” cuando la entrada a y la
entrada b valen “1” y toma el valor “0” cuando alguna de
las dos entradas vale “0”.
Tabla de verdad y símbolo de la puerta AND

18. 3. Puertas lógicas
B) PUERTA AND (continuación)
Implementación de la puerta lógica mediante circuito eléctrico.
Si se pulsan los dos interruptores
(a y b estarían en estado “1”) la
bombilla se enciende (S= “1”). Si
no pulso alguno (a = “0” o b =“0”)
la bombilla se apaga (S = “0”).
Encapsulado comercial

19. 3. Puertas lógicas
C) PUERTA INVERSORA
Realiza la función negación lógica. La función toma
valor lógico “1” cuando la entrada a vale “0” y toma
el valor “0” cuando la entrada a vale “1”. También se
la conoce como función Inversión.
Tabla de verdad y símbolo del inversor o puerta NOT

20. 3. Puertas lógicas
C) PUERTA INVERSORA (continuación)
Implementación de la puerta lógica mediante circuito eléctrico.
Si el interruptor a está sin pulsar (“0”) la
bombilla está encendida (S= “1”). Si
pulso el interruptor (a = “1”) la bombilla
se apaga (S = “0”).
Encapsulado comercial

21. 3. Puertas lógicas
D) PUERTA NOR
Realiza la función suma lógica negada o función NOR. La función toma
valor lógico “1” cuando la entrada a y la entrada b valen “0” y toma el
valor “0” en el resto de los casos. Es la función contraria a la OR .
Tabla de verdad y símbolo de la puerta NOR
Encapsulado comercial

22. 3. Puertas lógicas
E) PUERTA NAND
Realiza la función producto lógico negado o función NAND. La función
toma valor lógico “1” cuando la entrada a y la entrada b valen “0” y toma
el valor “0” en el resto de los casos. Es la función contraria a la AND .
Tabla de verdad y símbolo de la puerta NAND
Encapsulado comercial

23. 4. Circuitos con puertas lógicas
Cualquier expresión del algebra de Boole se puede implementar con
puertas lógicas. Estos son un par de ejemplos:
Circuito con puertas lógicas

24. 4. Circuitos con puertas lógicas
Función de salida f = ā · b + b · c

25. Postulados, propiedades y teoremas del álgebra de
Boole

26. Definición y postulados del álgebra de Boole
Elemento simétrico o complementario
Propiedad conmutativa respecto de la suma: a + b = b + a
Propiedad conmutativa respecto del producto: a · b = b · a

27. Definición y postulados del álgebra de Boole
Elemento simétrico o complementario
Elemento neutro: a + 0 = a, a · 1 = a
Índice de la unidad

28. Definición y postulados del álgebra de Boole
Elemento simétrico o complementario
Propiedad distributiva respecto de la suma: a · (b + c) = a · b + a
· c
Propiedad distributiva del producto: a + (b · c) = (a + b) · (a + c)

29. Definición y postulados del álgebra de Boole
Elemento simétrico o complementario
Figura 1.8.
Elemento complementario: a + ā = 1, a · ā = 0

30. 5. Obtención de una función a partir de una tabla de verdad
 Hemos visto como obtener un circuito a partir de una función. Pero
¿cómo se ha obtenido la función?
La función se obtiene a partir de la tabla de la verdad
 Para obtener la función podemos hacerlo fijándonos en los “0” ó los
“1” de la variable de salida. En este curso sólo lo haremos con los “1”.

31. 5. Obtención de una función a partir de una tabla de verdad
Ejemplo sin simplificar la función:

32. 6. Resolución de problemas con puertas lógicas
Pasos a seguir:
1.- Identificar las entradas y salidas
2.- Crear la tabla de verdad
3.- Obtener la función simplificada
4.- Implementar la función con puertas de todo
tipo

33. 7. Simplificación de funciones. Método de Karnaugh
 Con el método mostrado pueden aparecer función muy
“largas” cuyo circuito necesite muchas puertas lógicas
 Para evitar esto se simplifican las funciones. El método
más utilizado es los mapas de Karnaugh.
 Pasos a seguir:
1. Dibujar un cuadrado o rectángulo con celdas
dependiendo del número de variables de entrada
Dos variables:
ayb
Cuatro variables:
a, b, c y d
Tres variables :a, b y c

34. 7. Simplificación de funciones. Método de Karnaugh
Pasos a seguir:
2.
3.
4.
5.
6.
En la zona superior e izquierda se colocan las posibles
combinaciones de las variables de entrada siguiendo el
orden del código de Gray (¡OJO!)
Se colocan los “1” de la función de salida (ver la tabla de la
verdad) en las celdas que correspondan
Agrupar los “1” en bloques de 2, 4 u 8. Para agrupar las
casillas deben ser adyacentes en horizontal o vertical
(¡nunca en diagonal!). Se trata de obtener el mínimo
número de grupos que incluyan TODOS las celdas con “1”.
A cada grupo le corresponde un término. Sólo se
mantienen las variables de entrada que no varían en ese
grupo, eliminando las otras. El término será el producto de
estas variables teniendo en cuenta que si dichas variables
valen “1” se usará su forma directa y si valen “0” se usará
su forma negada
El resultado es la suma de los términos de cada grupo.

35. 7. Simplificación de funciones. Método de Karnaugh
 Ejemplo: simplificación de la función del ejemplo anterior

36. 7. Simplificación de funciones. Método de Karnaugh
Ejemplo resuelto:
1.-Tabla de verdad
a
b
c
S
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
2.- Mapa de tres variables
3.- Agrupamos unos
4.- Función obtenida

37. 7. Simplificación de funciones. Método de Karnaugh
Ahora sólo falta realizar el circuito de esta función con puertas
lógicas

38. 7. Simplificación de funciones. Método de Karnaugh
En ocasiones, la salida de ciertas combinaciones de las
entradas nos puede dar igual que sean “0” o “1”. En ese caso
se colocan “X” en la tabla de la verdad y sus celdas se usan
como comodines:

39. Ejemplo resuelto de un
problema de electrónica digital
Para poner en marcha un motor se requiere tres interruptores (a, b y c)
de tal forma que el funcionamiento del mismo se produzca
únicamente en las siguientes condiciones:
• Cuando esté cerrado solamente b.
• Cuando estén cerrados simultáneamente a y b y no lo esté c.
• Cuando estén cerrados simultáneamente a y c y no lo esté b.
a) Crea la tabla de verdad que represente el funcionamiento del
circuito de control.
b) Obtén la función expresada como suma de productos (Minterms).
c) Obtén la expresión simplificada por Karnaugh de la función.
d) Implementa la función utilizando puertas lógicas de todo tipo.

40. 1.- Identificar las entradas y salidas
Entradas: serán los interruptores a, b y c.
Interruptor pulsado será “1” y no pulsado será “0”
Salida: será el motor que está controlado por los
interruptores.
Cuando la salida de la función valga “1” indicará
que en ese caso el moto funciona. r

41. 2.- Crear la tabla de verdad
Se realiza leyendo detenidamente
el enunciado del problema y
colocando los valores de la
variable de salida (M) en función
de las combinaciones de las
variables de entrada (a, b y c)

42. 3.- Obtener la función simplificada
A partir de la tabla de la verdad se obtiene la función
del motor M simplificada por Karnaugh

43. 4.- Implementar la función con
puertas de todo tipo

44. 8. Circuitos combinacionales integrados
• Circuito combinacional: las salidas SOLO
dependen del valor de las entradas (si las
entradas no varían, las salidas tampoco)
• Existen “chips” que realizan las funciones de
diferentes circuitos combinacionales. Estos
chips están compuestos de puertas lógicas.
Cuanto más compleja sea la función, más
puertas lógicas serán necesarias

45. 8. Circuitos combinacionales integrados
Las salidas SOLO dependen del valor de las entradas

46. 8. Circuitos combinacionales integrados
A. Codificadores
Tiene n entradas y m salidas
Sólo se activa una entrada a la vez. Cuando una entrada se
activa en la salida aparece una combinación en binario que
indica qué entrada se ha activado
Ejemplo: si se activa la entrad número 6 y hay 3 salidas, la
salida será 110 que es valor 6 en binario
La salida puede ser en binario BCD u otro código binario (por
ejemplo en código Gray)

47. 8. Circuitos combinacionales integrados
A. Codificadores
Ejemplo: Codificador decimal a binario BCD
PROBLEMA: Sólo funciona bien si se activa una sóla entrada. Si se activan 2
entradas suma las salidas correspondientes a dichas entradas. Para solucionar
esto se utilizan codificadores con prioridad (ej: tiene prioridad la entrada mayor
y no tiene en cuenta las entradas menores aunque estén activadas. Si se
activan a la vez el 2 y el 6, la salida muestra la codificación correspondiente a la
entrada 6)

48. 8. Circuitos combinacionales integrados
B. Decodificadores
 Tiene n entradas y m salidas que funciona de manera inversa al
codificador
 Las n entradas son codificaciones en binario. Para cada combinación de
las entradas se activa UNA única salida de las m que existen. Esta
salida activada es laaquella cuyo nnúmero de orden coincide con el
valor de la combinación binaria de las entradas
 EJ: En un decodificador binario BCD a decimal. Si al entrada es 0101(5
en binario), se activará SOLO la salida nº 5.

49. 8. Circuitos combinacionales integrados
B. Decodificadores
Ejemplo1: Decodificador binario BCD a decimal
OBSERVACIÓN: Los decodificadores no tienen problemas de prioridad

50. 8. Circuitos combinacionales integrados
B. Decodificadores
Ejemplo2: Decodificador binario BCD a 7 segmentos
Las entradas son en biario BCD. El número correspondiente a
la entrada se puede ver en un display de7 segmentos
Display 7 segmentos:
Tiene 7 segmentos para formar números
Cada segmento es un diodo LED que se ilumina
al circular corriente por el.
Ejemplo: si a la entrada tenemos un 0011 (3),
se activan las salidas que están unidas a los
segmentos a,b, g, c y d para que se enciendan
y el display marque un “3”.

51. 8. Circuitos combinacionales integrados
2.2 Decodificadores
Ejemplo2: Decodificador binario BCD a 7 segmentos

52. 8. Circuitos combinacionales integrados
1.
2.
3.
4.
B. Decodificadores
Obtención de funciones con decodificadores:
Pasos:
El decodificador debe tener el mismo nº de entradas que el
nº de variables de la función
La función debe ser suma de productos
Conectamos las variables a las entradas del decodificador
(en orden)
Seleccionamos las salidas cuyo número de orden coincide
con los términos de la función y las conectamos a una puerta
OR. La salida de la puerta es la función que buscamos

53. 8. Circuitos combinacionales integrados
B. Decodificadores
Obtención de funciones con decodificadores:

54. 8. Circuitos combinacionales integrados
C. Demultiplexores
 Realizan la función inversa a un multiplexor
 Con una única entrada se elige por medio de unas entradas
de control por cuál de las salidas se enviará el dato
 Posee 1 entrada, 2n salidas y n entradas de control

55. 8. Circuitos combinacionales integrados
C. Demultiplexores
Ejemplo1: Multiplexor de 1 a 4 (1 entrada y 4 salidas)
Dependiendo del valor de las entradas de control C1 y C2, el
valor de la entrada (E) se coloca en un de las salidas (S0 a S3)

56. 8. Circuitos combinacionales integrados
D. Multiplexores
 Circuito combinacional que, de entre varias entradas, selecciona una de
ellas y la coloca a la salida
 Para la selección de la entrada utiliza Entradas de control
 Con n entradas de control se consigue elegir de entre 2 n entradas. La
elegida es la que se envía a la salida
 EJ: En un decodificador binario BCD a decimal. Si al entrada es 0101(5
en binario), se activará SOLO la salida nº 5.

57. 8. Circuitos combinacionales integrados
D. Multiplexores
Ejemplo; Multiplexor de 4 a 1 (4 entradas y una salida)
Esquema y tabla de la verdad
Dependiendo del valor de las entradas de control S1 y S2, se
elige el valor de una de las entradas (de D0 a D1) y se coloca
en la salida (Y)

58. 8. Circuitos combinacionales integrados
E. Comparadores
 Circuito que se utiliza para comparar 2 números binarios.
 Tiene 2 entradas para las dos magnitudes a y b (cada
entrada puede tener n bits) y 3 salidas para mostrar la
relación (a=b; a<b ó a>b)
 Ejemplo: comparador de 1 bit
 Otro ejemplo: comparador de 4 bits CI7485

59. 8. Circuitos combinacionales integrados
E. Comparadores
 Otro ejemplo: comparador de 4 bits CI7485

60. EN RESUMEN