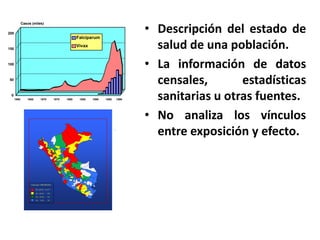
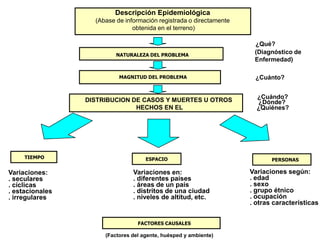
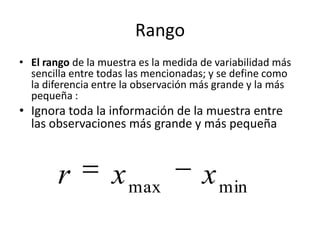
La epidemiología descriptiva resume información sobre casos según variables como tiempo, lugar y persona. Describe la frecuencia con la que ocurren eventos de salud en una población sin analizar vínculos entre exposición y efecto. Ofrece medidas como razones, tasas y estadísticas descriptivas para generar hipótesis sobre posibles factores causales.

1. EPIDEMIOLOGÍA DESCRIPTIVAInt. Gabriela Prutsky

2. DefiniciónLa epidemiológica descriptiva organiza y resume la información de los casos de acuerdo al Tiempo, Lugar y Persona. Estas tres características son llamadas variables epidemiológicas.

3. Casos (miles)200FalciparumVivax150100500196019651970197519801985199019951999Descripción del estado de salud de una población. La información de datos censales, estadísticas sanitarias u otras fuentes.No analiza los vínculos entre exposición y efecto.

4. La descripción epidemiológica se basa en la medición de la frecuencia con que ocurren diferentes sucesos.NO hay comparación entre poblaciones.Primera etapa de un estudio epidemiológico y genera hipótesis causales.

5. Hipótesis estadísticasNulas: Refutan o niegan las afirmaciones hechas en las hipótesis de investigaciónAlternativas: Son posibilidades alternativas ante las hipótesis nulas.Es un enunciado en desacuerdo con las hipótesis nulasCuando la hipótesis nula se rechaza es la conclusión

6. Hipótesisdeinvestigación No Asociativa: no establece asociación entre variables; son hipótesis simples. Es típico de un estudio descriptivo.Asociativa: Aquella que enlaza las variables. Pueden ser:Sin relación de dependencia o CorrelacionalesCon relación de dependencia o Causales

7. ¿Qué análisis pueden efectuarse a los datos?Estadística descriptiva.Razones, tasas y medidas de tendencia central.Búsqueda de significancía estadística.Análisis multivariados.

8. Estadística descriptivaSe realiza una distribución de frecuencias, indicando las cifras absolutas y relativas (porcentajes)

9. Descripción Epidemiológica(Abase de información registrada o directamente obtenida en el terreno)Variaciones según:Variaciones en:Variaciones:. edad. diferentes países. seculares. sexo. áreas de un país. cíclicas. grupo étnico. distritos de una ciudad. estacionales. ocupación. niveles de altitud, etc.. irregulares. otras características¿Qué?(Diagnóstico deEnfermedad)NATURALEZA DEL PROBLEMA¿Cuánto?MAGNITUD DEL PROBLEMA¿Cuándo?DISTRIBUCION DE CASOS Y MUERTES U OTROS HECHOS EN EL¿Dónde?¿Quiénes?TIEMPOESPACIOPERSONASFACTORES CAUSALES(Factores del agente, huésped y ambiente)

10. Fuentes de información en epidemiología Descriptiva

11. Datos vitalesAcontecimientos que se producen durante la vida de las personas.Son una fuente básica de datos para la Epidemiología. La finalidad de estos registros es jurídica.Nacimientos, defunciones, casamientos, adopciones, separaciones, etc.

12. DatosdemográficosDados por el censo, estos deben realizarse cada 10 años.La información que se obtiene es:Cantidad de población

13. Distribución: geográfica,

14. edad, sexo, etc.

15. Migración.

16. Características de vivienda.

17. Niveles socio económicos.Datos de morbilidadInformación proveniente de los establecimientos de saludSe cuenta con los siguientes datos: Egresos Hospitalarios.

18. Datos de Consulta Externa

19. Datos de EmergenciaVigilancia Epidemiológica

20. Otras fuentes de datos importantesLos datos anteriores no son suficientes para un adecuado conocimiento de la situación de salud de una población, es necesario incluir en el análisis otros indicadores, como los de nutrición, acceso a servicios básicos, escolaridad, empleo y condiciones de trabajo, entre otros.

21. Medidas de epidemiología descriptiva

22. Las medidas descriptivas más comunes de tendencia central o localización son: la mediaaritmética y la mediana(existen otras medidas de tendencia central que en ocasiones pueden resultar de interés: la moda, los cuartiles, los deciles, los percentiles, la media armónica, la media geométrica y la media ponderada.)

23. Media aritmetica o PromedioLa media aritmética o simplemente promedio (también llamada media muestral ya que generalmente se calcula en relación a una muestra) se calcula de la siguiente forma: si las observaciones de una muestra de tamaño n son x1, x2,…,xn entonces

24. Característica de la MediaEs intuitiva y fácil de calcular.Su valor puede que no coincida con ninguno de los valores de la muestraLa suma de las diferencias de cada valor de la muestra con la media su resultado es cero, es decir,

25. MedianaLa mediana se suele definir como el valor “más intermedio” una vez que los datos han sido ordenados en forma creciente.

26. MedianaLa mediana es aquel valor que deja el cincuenta por ciento de los datos por debajo y otro cincuenta por encima.Cabe destacar que es preferible el uso de la mediana como medida descriptiva del centro cuando se quiere reducir el efecto de valores extremos en un conjunto de datos (muy grandes o muy pequeños).

27. ModaEs una medida de tendencia central La moda de un conjunto de observaciones es el valor que más se repite. Puede ser única, que haya más de una, o que no exista.

28. Media Geométrica:Se define como la raíz n-ésima del producto de todos los valores numéricos, es decir,

29. La media armónicaSe define como el número de observaciones de la muestra dividido por la suma del inverso de cada una de las observaciones, es decir,

30. DispersiónDispersión reducida si los mismos se aglomeran estrechamente en torno a alguna medida de localización de interés Dispersión grande si se esparcen ampliamente alrededor de alguna medida de localización de interés. Las medidas descriptivas más comunes de dispersión son: el rango, la varianza, la desviación estándar y el rango intercuartílico.

31. RangoEl rango de la muestra es la medida de variabilidad más sencilla entre todas las mencionadas; y se define como la diferencia entre la observación más grande y la más pequeña :Ignora toda la información de la muestra entre las observaciones más grande y más pequeña

32. VarianzaEn general, se desea una medida de variabilidad que dependa de todas las observaciones y no sólo de unas pocas; así que parece razonable medir la variación en términos de las desviaciones relativas a alguna medida de localización (generalmente esta medida es la media) -> VARIANZA

33. Desviación estandar La raíz cuadrada (positiva) de la varianza a fin de tener una medida en las mismas unidades de los datosútil para comparar dispersión entre dos poblaciones, pero también lo es para calcular el porcentaje de la población que pueden localizarse a menos de una distancia específica de la media.