El documento presenta la asignatura de 'Estrategias de Programación y Estructuras de Datos' en el Grado en Ingeniería Informática y Tecnologías de la Información de la UNED, incluyendo detalles sobre el equipo docente, objetivos generales, y contenidos. Los temas abarcan desde estructuras de datos y programación orientada a objetos hasta principios de diseño y análisis de algoritmos. También se especifican las evaluaciones y el trabajo requerido para los estudiantes a lo largo del curso.


























![Introducción
Javier Vélez Reyes jvelez@lsi.uned.es1 - 22
Programación orientada a objetos
Fundamentos de la programación orientada a objetos
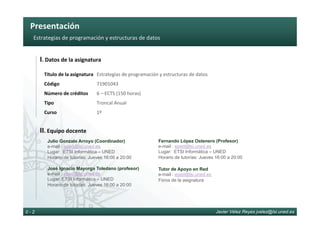
VI. Genericidad
Lo que convierte a la programación orientada a objetos en el paradigma idóneo para
realizar diseño de sistemas centrados en abstracciones de datos es el uso de 6
caracterís6cas fundamentales: abstracción, encapsulación, herencia, polimorfismo, ligadura
dinámica y genericidad
La genericidad permite abstraerse de las los 6pos de objetos con los que trabaja
internamente una clase por medio de la parametrización de los mismos. De hecho esta
caracterís6cas es también conocida como parametrización de 6pos
PilaDeCoches
PilaDeMotos
Genericidad
Pila <T>
+ apilar (T t)
+ T desapilar ()
- Moto pila []
- Coche pila []
+ apilar (Coche p)
+ Coche desapilar ()
+ apilar (Moto m)
+ Moto desapilar ()
- T pila []](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-30-320.jpg)

















![Estrategias de programación
Javier Vélez Reyes jvelez@lsi.uned.es2 - 11
Diseño de algoritmos recursivos
Diseño de algoritmos recursivos
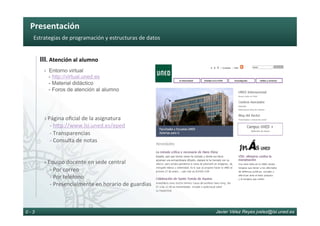
Diseño de recursividad por inmersión
Como hemos visto, la tarea de diseño de una función recursiva consiste en la definición de
la colección de casos base y casos recursivos que resuelvan sa6sfactoriamente el problema.
A con6nuación discu6mos el correcto diseño de cada 6po de caso
A veces el diseño de una función recursiva se expresa como una invocación concreta de
una función más general que incluye parámetros adicionales. Esta técnica, conocida por
el nombre de diseño por inmersión, se aplica por dis6ntas cues6ones que discu6remos a
con6nuación
La inmersión es una estrategia de diseño mediante la cual
una función se expresa como una invocación particular de
otra función más general con parámetros adiciones
int sumaTodos (int v[]) {
return sumaDesde (v, 0);
}
int sumaDesde (int v[], int index) { ... }
Función inmersora
La función inmersora
sumerge a la original puesto
que, al ser más general, con
una invocación par6cular de
ésta se da cobertura al
problema
Función sumergida
La función sumergida
se expresa como una
invocación concreta de
la función inmersora
más general](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-48-320.jpg)




![Estrategias de programación
Javier Vélez Reyes jvelez@lsi.uned.es2 - 16
Diseño de algoritmos itera6vos
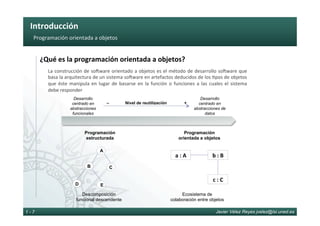
¿Qué son los algoritmos itera8vos?
En los algoritmos itera6vos los problemas se resuelven mediante la escritura de una
colección de instrucciones de propósito específico que se ejecutan de manera secuencial
según el orden en que se han escrito. Algunas de estas instrucciones permiten alterar el
control secuencial de la ejecución para ar6cular flujos itera6vos o condicionales de
ejecución
Esquema general de un algoritmo itera8vo
int está (T[] v, T e) {
int index = 0;
boolean found = false;
while (!found && index < v.length) {
found = (v [index] == e);
if (!found) index++;
}
if (found) return index;
else return -1;
}
La inicialización es el paso
preliminar para proceder con el
diseño itera6vo de algoritmos
Inicialización
Iteración
Los algoritmos itera6vos basan su
funcionamiento en iteraciones de
bloques de código generalmente
aplicadas sobre elementos de
estructuras de datos
Bifurcación
Las instrucciones de control de
flujo condicional permiten ejecutar
sentencias solo bajo determinadas
condiciones ambientales
Secuenciamiento
La caracterís6ca esencial del diseño itera6vo radica en el
concepto de secuencia de instrucciones ejecutadas en orden
y en el uso de variables para acumular estados parciales](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-53-320.jpg)





![Estrategias de programación
Javier Vélez Reyes jvelez@lsi.uned.es2 - 22
Diseño de algoritmos itera6vos
Diseño de algoritmos itera8vos
El diseño itera6vo u6liza instrucciones que prescriben cómo realizar los cálculos o tareas
necesarias para llegar al resultado buscado. Estas instrucciones se ejecutan de acuerdo a
flujos de ejecución, que pueden ser secuenciales, bifurca6vos e itera6vos. La u6lización de
variables y la sentencia de asignación juegan un papel preponderante
Ejercicios
Encuentre una solución itera6va para
cada uno de los problemas que se
presentaron con anterioridad
I. Función factorial
II. Serie de fibonacci
III. Potencia de un número
IV. Suma de N naturales
V. Suma de un vector
VI. Producto escalar
VII. Búsqueda en vector
VIII. Elementos repetidos
IX. Máximo común divisor
// Pre: -1 < j <= length
public int sumaV (int[] v) {
int j = 0;
int s = 0;
while (j < v.length) {
s = s + v[j];
j++;
}
return s;
}
// Post: s = Σ v[i]
i=0
length](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-59-320.jpg)
![Estrategias de programación
Javier Vélez Reyes jvelez@lsi.uned.es2 - 23
Traducción de algoritmos recursivos a itera6vos
Traducción de algoritmos recursivos a itera8vos
Los algoritmos recursivos aunque elegantes y eficaces han presentado problemas históricos
de computabilidad ya que el soporte por parte de los compiladores a la invocación recursiva
de programas es rela6vamente reciente. Merece la pena discu6r procedimientos de
transformación de algoritmos recursivos a itera6vos
Traducción de algoritmos con recursividad final
public int sumaV (int[] v, int j, int w) {
if (j >= n) return w
else return sumaV (v, j+1, v[j] + w)
}
public int sumaVit (int [n] v) {
int j = 0;
int w = 0;
while (j < n) {
w = w + v[j];
j = j + 1;
}
return w;
}
Los parámetros de entrada se subs6tuyen por
variables locales con el valor que recibirían en la
llamada inicial (j). El parámetro acumulador (w)
juega el papel del resultado parcial inicialmente 0.
Dentro del bucle se calcula el valor,
en cada paso, de las variables de
resultado parcial w y de recorrido j](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-60-320.jpg)










![Análisis de la eficiencia de los algoritmos
Javier Vélez Reyes jvelez@lsi.uned.es3 - 5
Introducción
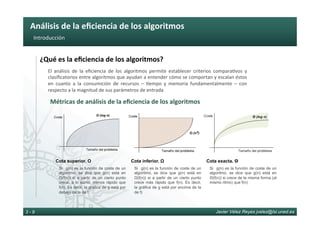
¿Qué es la eficiencia de los algoritmos?
El análisis de la eficiencia de los algoritmos permite establecer criterios compara6vos y
clasificatorios entre algoritmos que ayudan a entender cómo se comportan y escalan éstos
en cuanto a la consumición de recursos – 6empo y memoria fundamentalmente – con
respecto a la magnitud de sus parámetros de entrada
boolean contiene (T[] v, int p, T e) {
int i = p;
boolean found = false
while (!found && i <= v.length) {
found = (v[i] == e);
i = i + 1;
}
return found; }
boolean repetidos (T[] v) {
boolean repetidos = false;
int i = 0;
while (!repetidos && i < v.length)
repetidos = contiene (v, i+1, v[i]);
return repetidos;
}
boolean ordenar (T[] v) {
int temp;
for (int i = 1; i < v.length; i++)
for (int k = v.length - 1; k >= i; k--)
if (v[k] < v[k-1]) {
temp = v[k];
v[k] = v[k-1];
v[k-1] = temp;
}
}
<
tiempo](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-71-320.jpg)











![Análisis de la eficiencia de los algoritmos
Javier Vélez Reyes jvelez@lsi.uned.es3 - 18
Medida de la eficiencia de los algoritmos
¿Cómo se mide la eficiencia de los algoritmos?
La medida de la eficiencia asintó6ca de algoritmos pretende clasificar cada algoritmo en
una familia de complejidad asintó6ca determinada prescindiendo de consideraciones
constantes o de escala. En nuestro estudio u6lizaremos medida temporal, caso peor y cota
superior
Algoritmos itera8vos
.
A par6r de los análisis anteriores de coste
de cada instrucción analicemos la
eficiencia de un algoritmo itera6vo
boolean ordenar (T[] v) {
int temp;
for (int i = 1; i < v.length; i++) O(1)
for (int k = i+1; k < v.length; k++) O(1)
if (v[i] < v[k]) { O(1) O(n2)
temp = v[k]; O(1)
v[k] = v[i]; O(1) O(1) O(1)·(n-i) O(n)·n
v[i]= temp; O(1)
}
}
max max max max](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-84-320.jpg)





![Tipos Abstractos de Datos
Javier Vélez Reyes jvelez@lsi.uned.es4 - 4
Introducción
¿Qué son los 8pos abstractos de datos?
Definiciones
La caracterización formal y precisa de lo que entenderemos en este curso por 6po abstracto
de datos parte de una diferenciación previa fundamental entre tres conceptos: 6po
abstracto de datos, 6po de datos y estructura de datos
Una estructura de datos es una representación computacional de la
organización de un conjunto de datos ar6culada en términos de 6pos de
datos primi6vos y otras estructuras o 6pos del lenguaje
Un 6po de datos es la definición de una estructura de datos por parte del
usuario programador para incluirla como un nuevo concepto nominal que
forme parte de las en6dades semán6cas del problema
Un 6po abstracto de datos es un modelo formal de organización de datos
caracterizado por cierto comportamiento semán6co definido en términos
de una colección de propiedades axiomá6cas y operaciones. Dicho
modelo es prescrip6vamente independiente de sus posibles
implementaciones subyacentes y responde a un patrón de uso recurrente
I. Estructura de Datos
II. Tipo de datos
III. Tipo abstracto de datos
- Book elements []
+ void push (Book b) {...}
+ Book pop () {...}
BookStack
T elements []
Stack <T>
+ void push (T e)
+ T pop ()](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-90-320.jpg)






























































![Tipos abstractos de datos lineales. Colas
Javier Vélez Reyes jvelez@lsi.uned.es6 - 13
Algoritmos sobre colas
Búsqueda de un elemento sobre una cola
La búsqueda de un dato sobre los elementos contenidos en una cola es un problema de
recorrido secuencial que termina cuando se encuentra una cabeza que corresponde con el
dato buscado. Dado que el 6po no 6ene una definición recursiva, el problema de búsqueda
no se presta a este 6po de resolución algorítmica. A con6nuación presentamos dos
versiones de la búsqueda itera6va con cen6nela que aprovechan la estructura interna de la
implementación del 6po
Búsqueda en QueueDynamic
@Override
public boolean contains (T element){
boolean found = false;
Node<T> node = first;
while (!found && node != null) {
found = node.getElement ().equals (element);
node = node.getNext ();
}
return found;
}
Es esta implementación se realiza una
búsqueda con cen6nela sobre la estructura
de nodos enlazados que implementar el 6po
cola
Búsqueda en QueueSta8c
@Override
public boolean contains (T element)
{
boolean found = false;
int index = first;
while (!found && Math.abs (last - index) > 0) {
found = elements [index].equals (element);
index = next (index);
}
return found;
}
En la implementación está6ca los datos son
almacenados sobre una estructura vectorial
que debe ser recorrida circularmente desde
el primero hasta el úl6mo elemento, si el
cen6nela no lo impide](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-153-320.jpg)

















































![Tipos abstractos de datos jerárquicos. Árboles binarios
Javier Vélez Reyes jvelez@lsi.uned.es8 - 23
Algoritmos sobre árboles binarios
Árboles binarios de búsqueda
Tipos de árboles de búsqueda
Los árboles binarios de búsqueda son u6lizados para disponer los elementos de un
conjunto de tal forma que se op6mice la localización de los mismos alcanzándose un coste
temporal logarítmico con respecto al volumen de datos medido para el peor caso. La
disposición de los elementos debe seguir, naturalmente, ciertos criterios de orden
Dado que la restricción acerca del equilibrio es demasiado fuerte, se han ideado algunos
6pos de árboles de búsqueda cuasi-equilibrados que aplican las rotaciones anteriores como
eje fundamental del mantenimiento logarítmico de las operaciones de localización
Árboles AVL Árboles roji – negros
En los árboles AVT las alturas de los hijos izquierdo y
derecho de cada subárbol sólo pueden diferir, a lo sumo
en una unidad aplicándose rotaciones para el
reequilibrado. Inserción y borrado son logarítmicas. La
primera debido a un coste constante de la rotación. La
segunda porque la propagación solo se exAende hasta la
raíz Para el resto de operaciones, el coste temporal,
tanto promedio como en el caso peor, es también
logarítmico aunque su coste espacial resulta lineal.
[Weiss, 484-492] [Drozdek, 255-260]
Los árboles roji-negros son estructuras auto-equilibradas en
la que los nodos Aenen un atributo adicional, su color (rojo o
negro). La raíz es siempre negra. Los dos hijos de un nodo
rojo deben ser negros. Todas las hojas son negras. Y todos los
caminos desde un nodo antecesor hasta cualquiera de sus
hojas deben contener el mismo número de nodos negros. Se
uAlizan rotaciones para reequilibrar. Se pueden eliminar el
segundo recorrido de los AVL mediante una transformación
descendente de algunos de los nodos (cambio de color,
inserción de una hoja y rotación). Sin embargo, el borrado
Aene una codificación compleja. Su coste temporal es
logarítmico. [Weiss, 492-505]](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-203-320.jpg)
![Tipos abstractos de datos jerárquicos. Árboles binarios
Javier Vélez Reyes jvelez@lsi.uned.es8 - 24
Algoritmos sobre árboles binarios
Árboles binarios de búsqueda
Tipos de árboles de búsqueda
Los árboles binarios de búsqueda son u6lizados para disponer los elementos de un
conjunto de tal forma que se op6mice la localización de los mismos alcanzándose un coste
temporal logarítmico con respecto al volumen de datos medido para el peor caso. La
disposición de los elementos debe seguir, naturalmente, ciertos criterios de orden
Dado que la restricción acerca del equilibrio es demasiado fuerte, se han ideado algunos
6pos de árboles de búsqueda cuasi-equilibrados que aplican las rotaciones anteriores como
eje fundamental del mantenimiento logarítmico de las operaciones de localización
Árboles AA Árboles B
Los árboles AA son una variante de los roji-negros cuyo
atributo adicional es el nivel en lugar del color. El nivel
representa el número de enlaces a hijos izquierdos en el
camino hacia la hoja (para las hojas 1). Un padre rojo y
su hijo se conectan por un enlace horizontal y Aenen el
mismo nivel. El nivel del hijo de un padre negro será una
unidad menos que el de su padre . La inserción siempre
se realiza en el nivel más bajo del árbol. Se uAlizan
rotaciones simples para reequilibrar si es preciso. El
borrado se limita a la eliminación de un nodo de nivel 1.
Su coste espacial y temporal es igual al de los rojinegros
aunque los árboles AA se suelen aplanar algo más.
[Weiss, 505-512]
Los árboles B son una generalización de los árboles binarios
de búsqueda en los que un nodo interno puede tener más de
dos hijos hasta un cierto límite. OpAmizan la lectura de
grandes bloques de datos. Un árbol B de orden k es un árbol
k-ario en que los datos se almacenan en las hojas. Un nodo
interno contendrá k-1 claves de búsqueda, donde la j-ésima
clave será la menor del árbol j+1-ésimo. La raíz bien será una
hoja bien tendrá un rango de hijos entre 2 y k. Los nodos
internos Aenen entre k/2 y k hijos. La profundidad de todas
las hojas es la misma y Aenen entre h/2 y h hijos, donde h es
un valor constante y prefijado. Al maximizar el número de
hijos la altura decrece reduciéndose el coste de acceso
(logaritmo en base k) y los reequilibrios. [Weiss, 512-519]](https://image.slidesharecdn.com/eped-170312115937/85/Estrategias-de-Programacion-Estructuras-de-Datos-204-320.jpg)