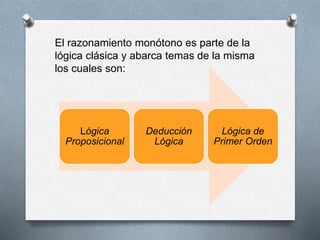
El razonamiento monótono utiliza contradicciones para llegar a conclusiones finales y es parte de la lógica clásica, que incluye la lógica proposicional y la lógica de primer orden. La lógica proposicional analiza argumentos mediante variables y operaciones lógicas, mientras que la lógica de primer orden estudia la inferencia en lenguajes de primer orden y puede definir casi todas las matemáticas. Ambos sistemas buscan clarificar la noción de consecuencia lógica a partir de premisas deducibles.

1. 2.5 Razonamiento
Monótono

2. El razonamiento monótono, es el que
utiliza contradicciones para procesar.
Elimina un hecho (factor de
conocimiento) obteniendo la
contradicción hasta que llega a una
conclusión final.
Concepto

3. Ejemplo
“Cuando se ve a una persona tirando basura en la
calle y pensamos en lo mal que se ve, la
criticamos, pero cuando realizamos el mismo acto
sin pensar, caemos en una contradicción y
concluimos que somos igual a la persona que
estaba tirando basura en la calle”.

4. El razonamiento monótono es parte de la
lógica clásica y abarca temas de la misma
los cuales son:
Lógica
Proposicional
Deducción
Lógica
Lógica de
Primer Orden

5. Que es la lógica?
La Lógica es la rama del
conocimiento
que se encarga de estudiar las
formas en que se pueden deducir
verdades de una forma válida.

6. Lógica proposicional
O Es un sistema formal diseñado para analizar
ciertos tipos de argumentos. En la lógica
proposicional, las fórmulas representan
proposiciones y las constantes lógicas son
operaciones sobre las fórmulas que
producen otras fórmulas de mayor
complejidad. Como otros sistemas lógicos, la
lógica proposicional intenta esclarecer
nuestra comprensión de la noción de
consecuencia lógica para el rango de
argumentos que analiza.

8. Variables proposicionales: p, q, r,…
Operaciones proposicionales: ¬(negación),
˅(disyunción)˄(conjunción)→(implicación)↔(bico
ndicional).
Signos auxiliares:[,].
Definición de formulas:
1.- Toda variable proposicional es una fórmula.
2- si A es una formula, entonces, ¬A es una
fórmula.
3.- si A y B son formulas, entonces,[A ˅ B],[A ˄
B],[A → B],[A ↔ B], son formulas.

9. Interpretación de fórmulas: las variables
proposicionales toman los valores de verdad:
1(verdadero)0(falso).
Definición de las operaciones proposicionales:
AB ¬A [A ˅ B] [A ˄ B] [A → B] [A ↔ B]
11 0 1 1 1 1
10 0 1 0 0 0
01 1 1 0 1 0
00 1 0 0 1 1

10. Deducción lógica
O Consiste en que a partir de unas premisas, representadas con
símbolos, y a través de unas reglas, obtenemos una
conclusión (deducimos la conclusión).
O De manera general, en lógica se considera siempre un
conjunto (conjunción) de proposiciones P= { C 1 , C 2 ,..., C
n } que constituirán lo que se denomina una teoría, una base
de conocimientos o un programa lógico. El objetivo
es establecer que una cierta proposición T es una
consecuencia lógica (es deducible) (es un teorema) de P lo
cual denotaremos por:
O C1, C2,…, Cn |= T

11. Se lee T es una consecuencia lógica de C1,
C2,…, Cn.
Sea, P1, P2, P3,…, Pn |= QSe define como
correcta, cuando no existe ninguna
interpretación que simultáneamente haga
P1, P2, P3,…, Pn verdaderos y Q falso, es
decir, cuando todo modelo de las premisas,
es un modelo de la conclusión.
O

12. Ejemplo: "si graniza (g) o nieva (n) entonces, uso
paraguas (p) o no salgo de casa (¬s) . Se da el
caso de que graniza (g) . Por lo tanto, no salgo de
casa (¬s) ".
La formalización de este argumento es la siguiente:
( g V n ) -> ( p V ¬s ) , g I- ¬s
EJEMPLO

13. Lógica de primer orden
O La lógica de primer orden, también
llamada lógica de predicados o cálculo de
predicados, es un sistema formal
diseñado para estudiar la inferencia en
los lenguajes de primer orden.
O La lógica de primer orden tiene el poder
expresivo suficiente para definir a
prácticamente todas las matemáticas.
Que es ?

14. O Una lógica de primer orden (LPO) consta de
un lenguaje L y un concepto de inferencia C,
con la siguiente caracterización:
O El lenguaje L se describe en sus dos
dimensiones fundamentales: Sintaxis y
Semántica.
O Sintácticamente L consta de un alfabeto y de
dos clases de expresiones bien definidas a
partir de los símbolos de este alfabeto:
términos y fórmulas.