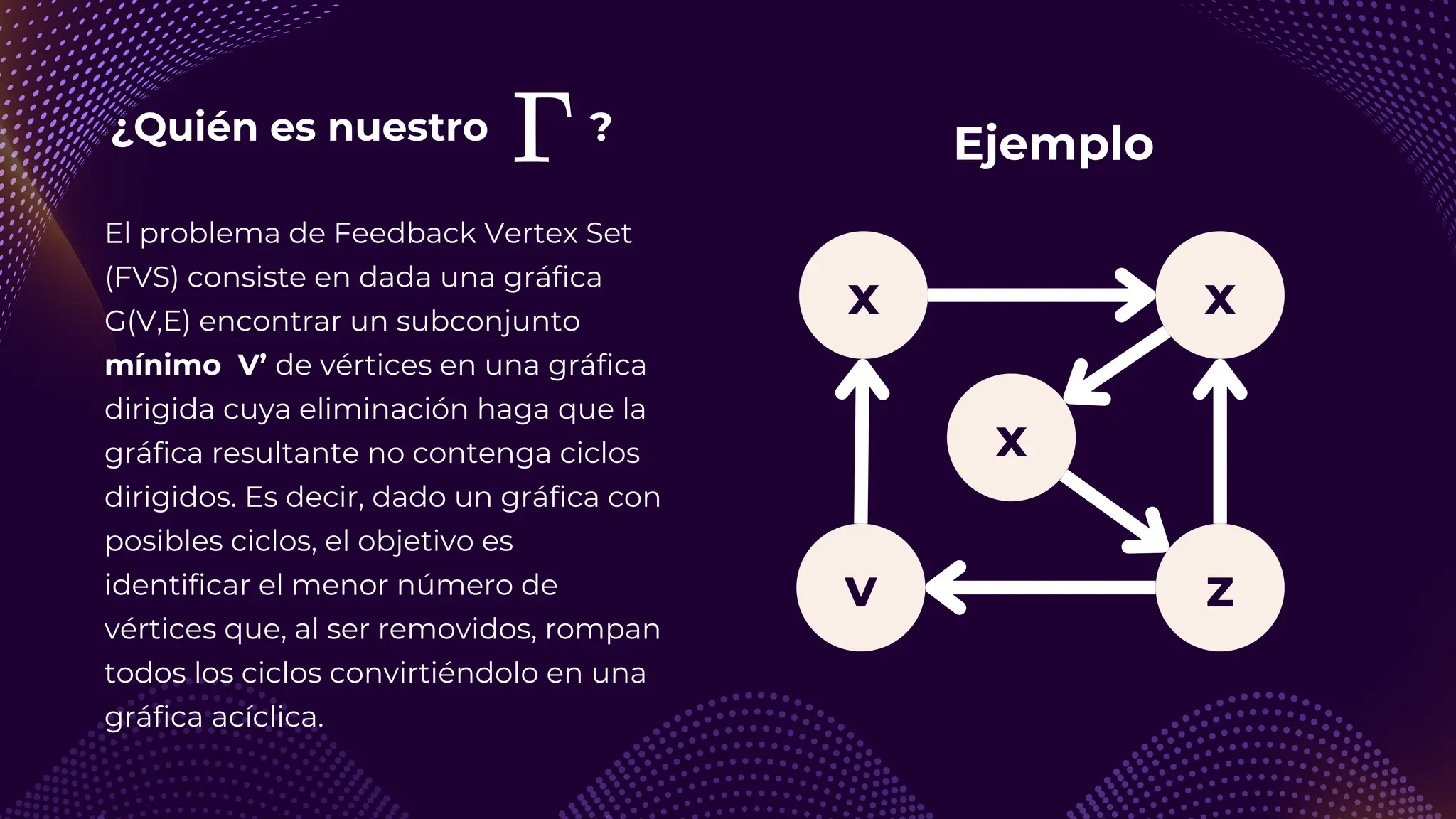
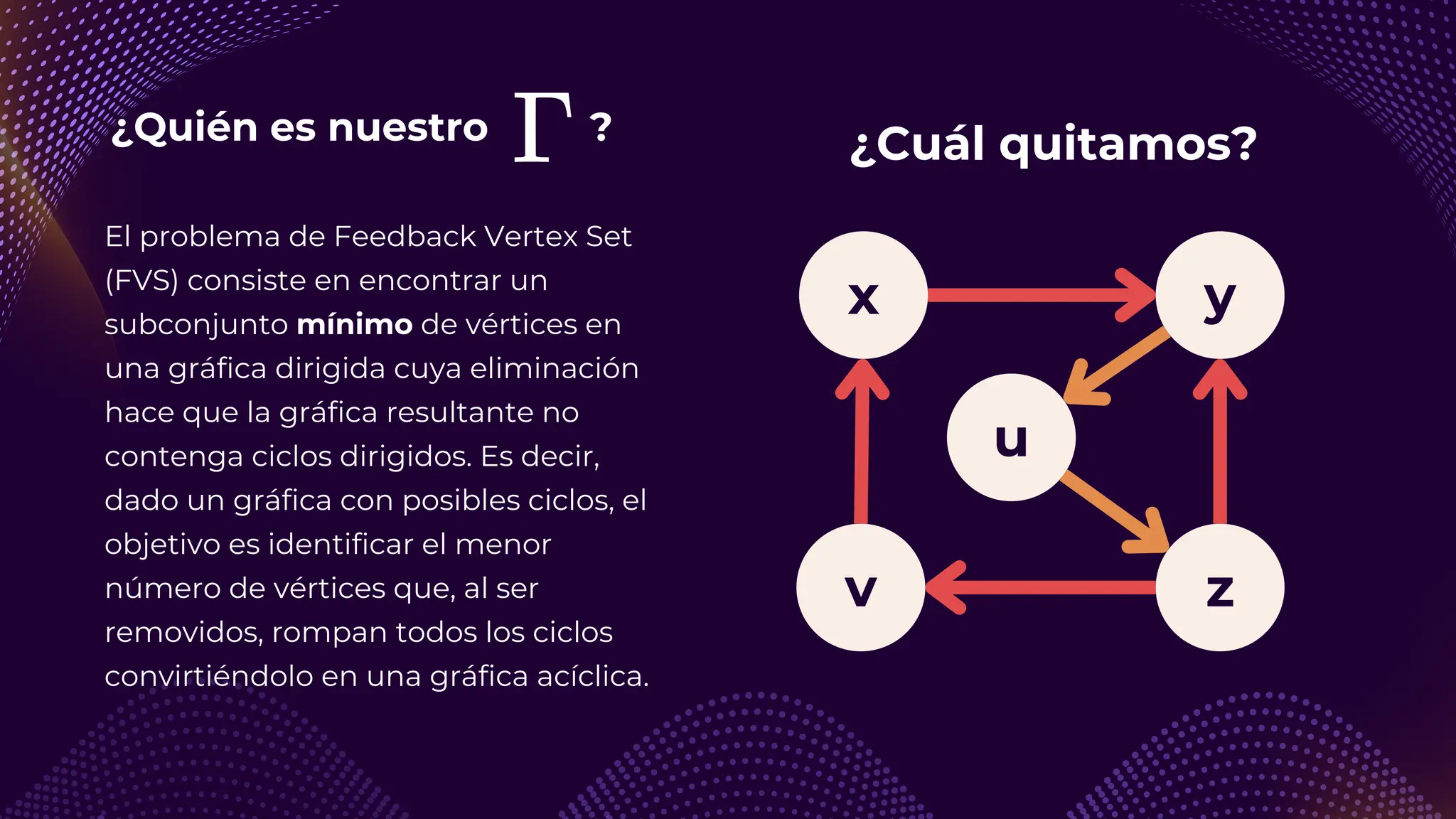
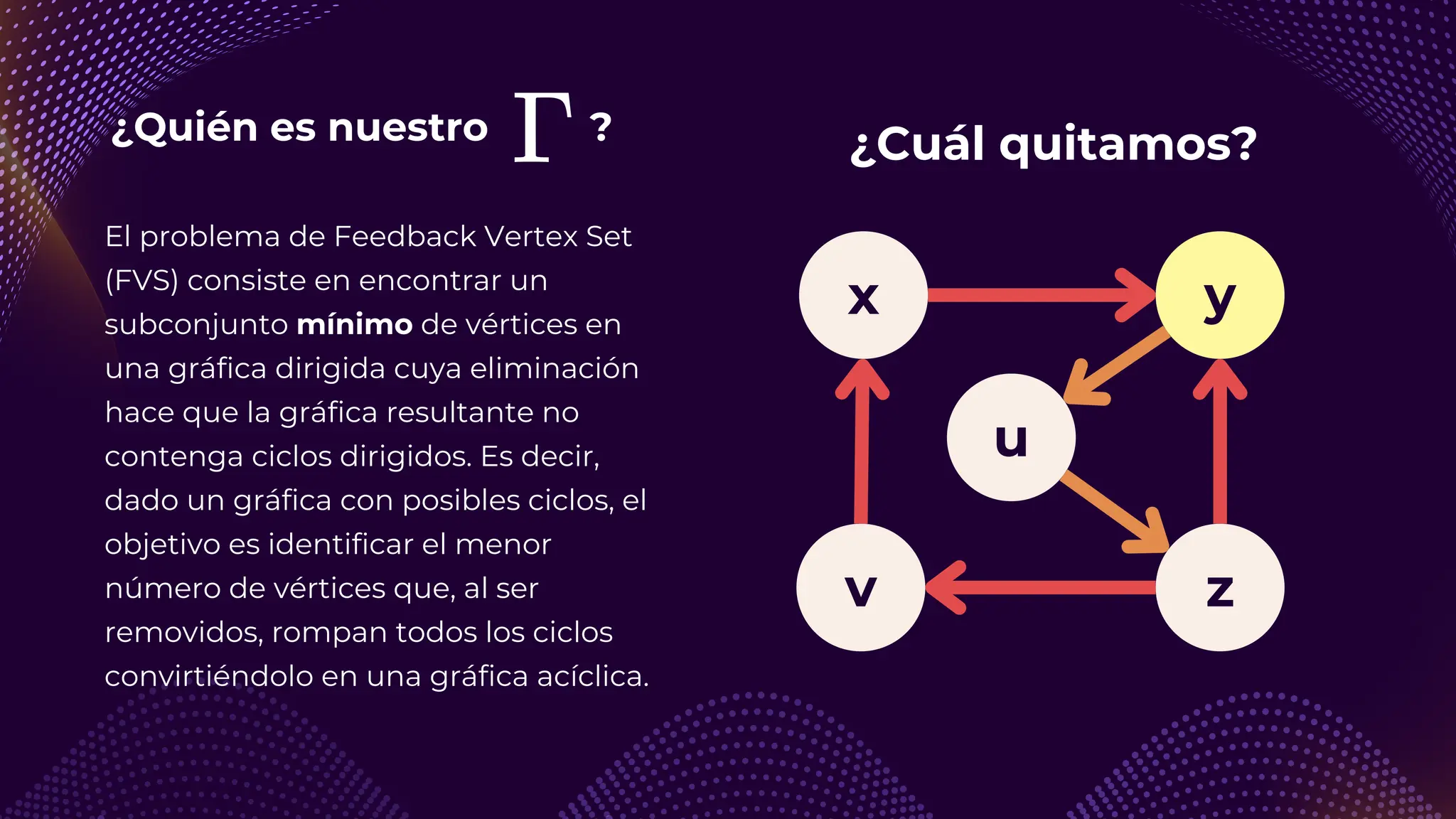
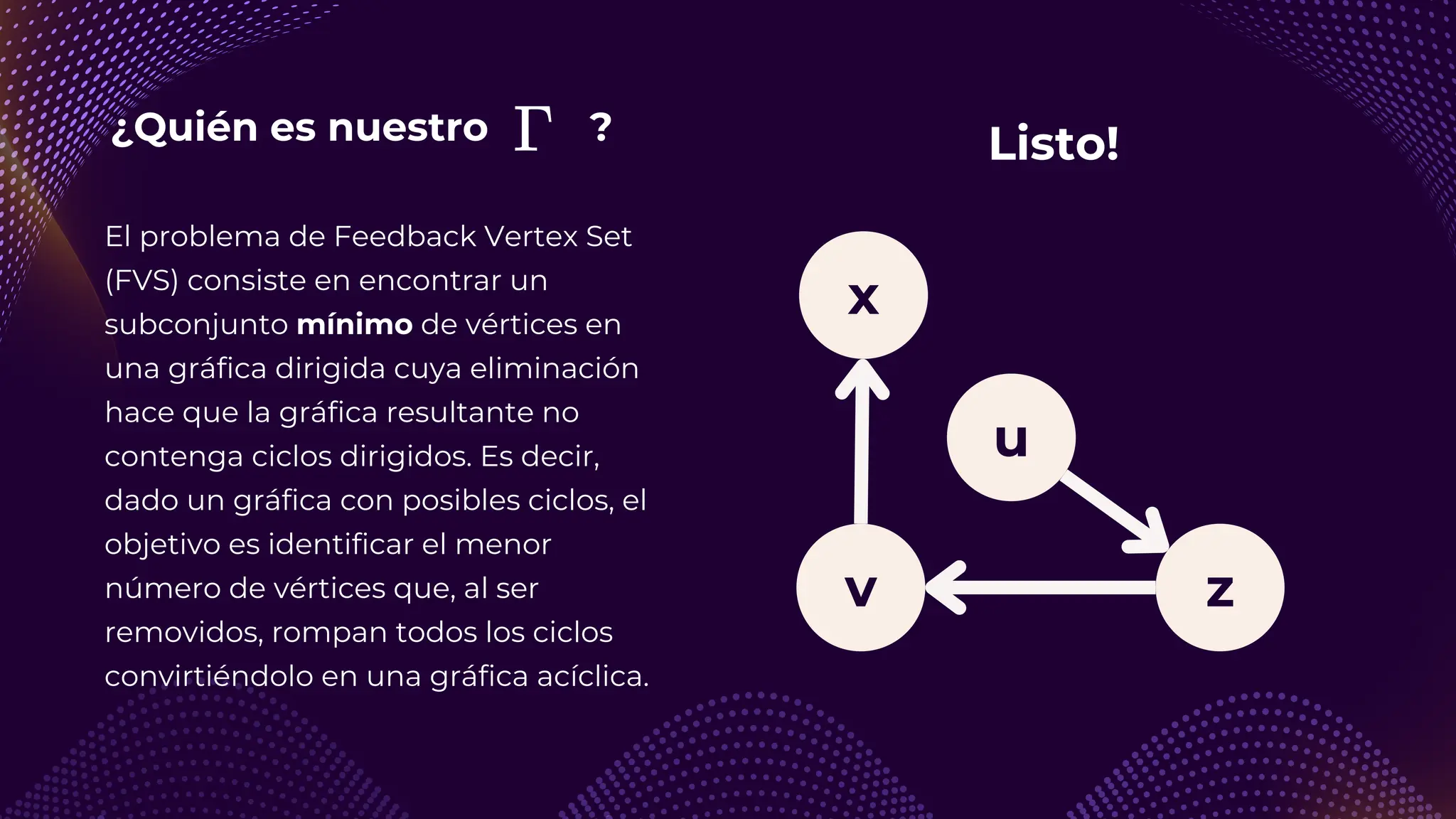
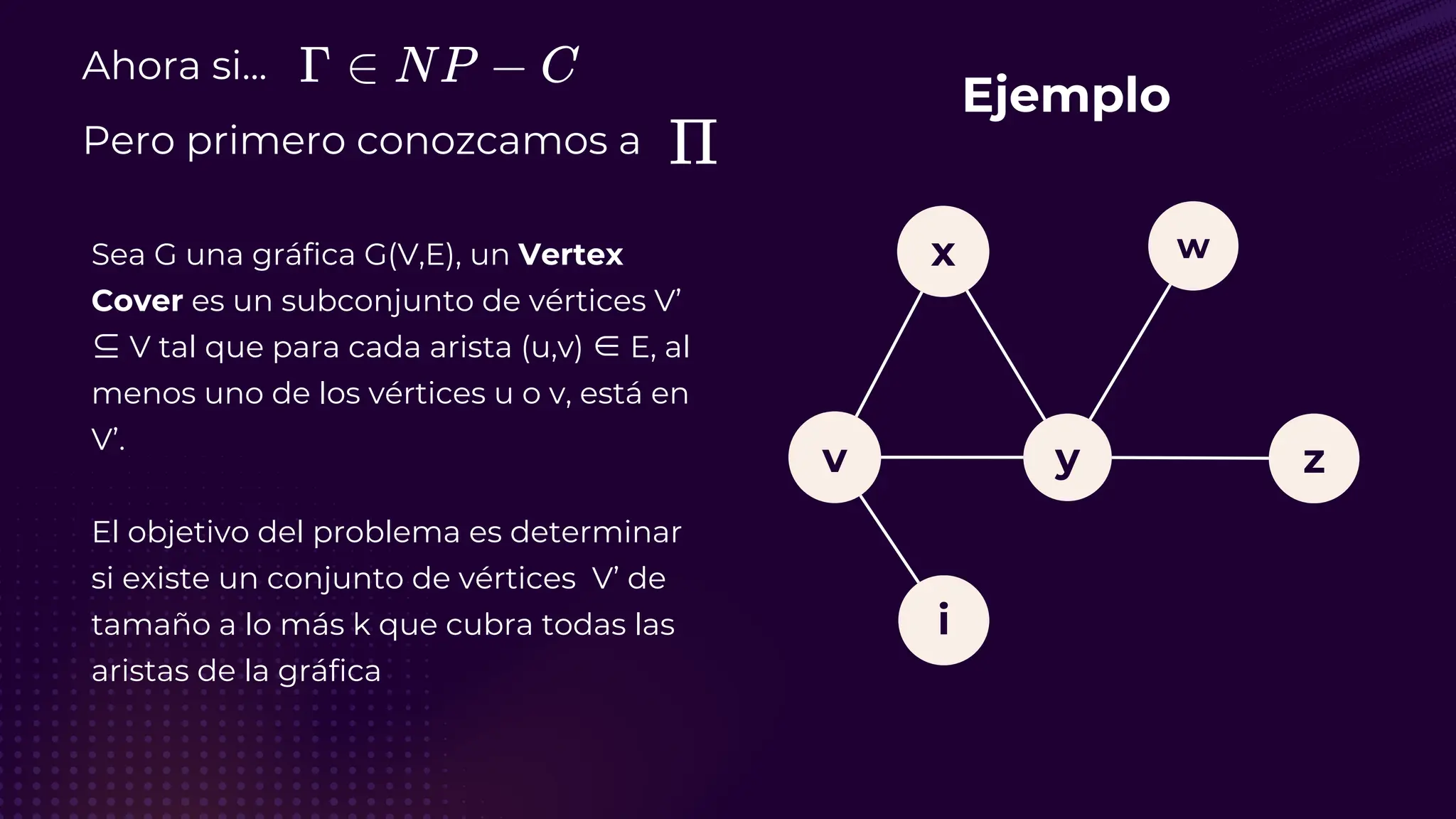
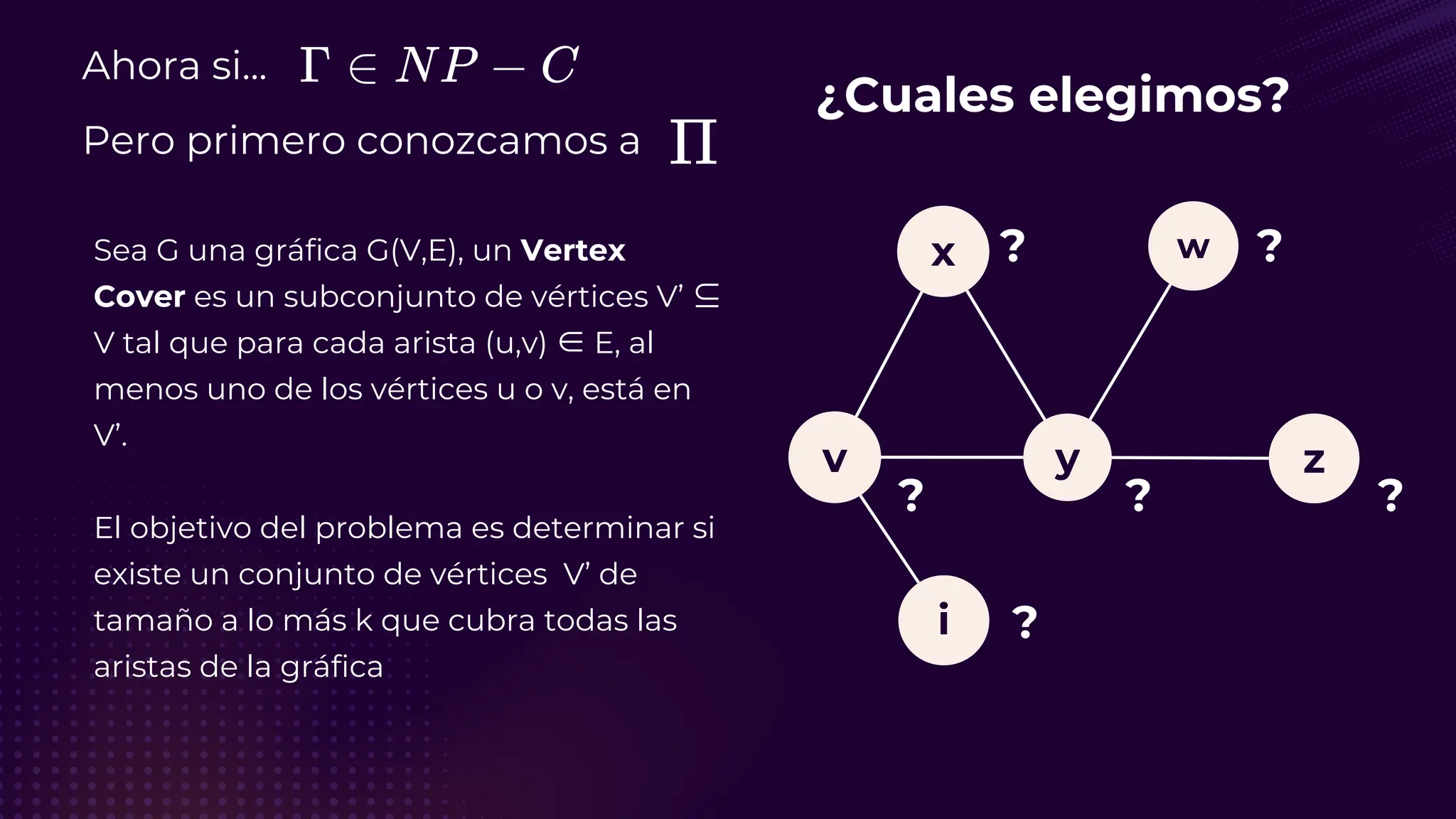
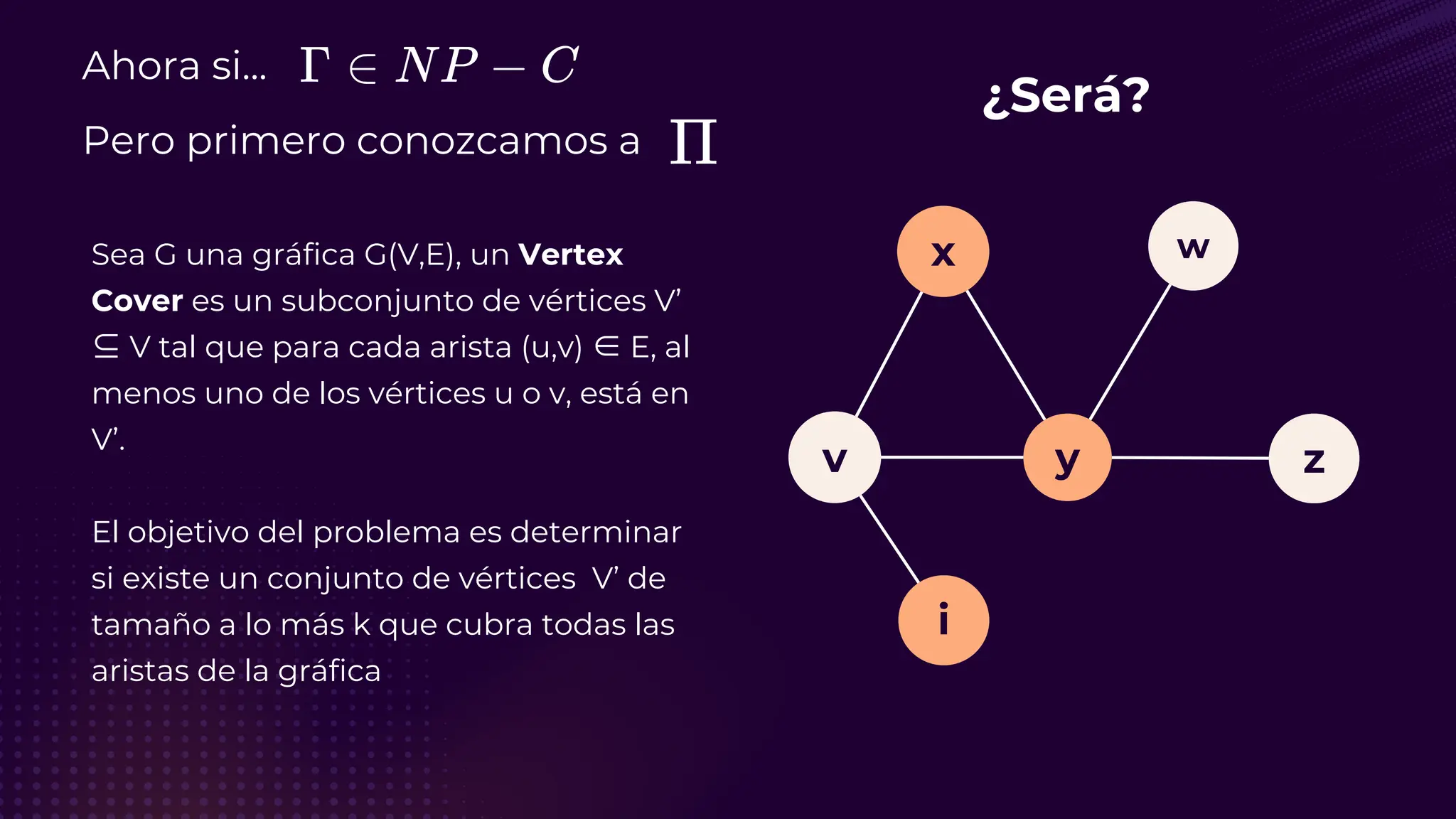
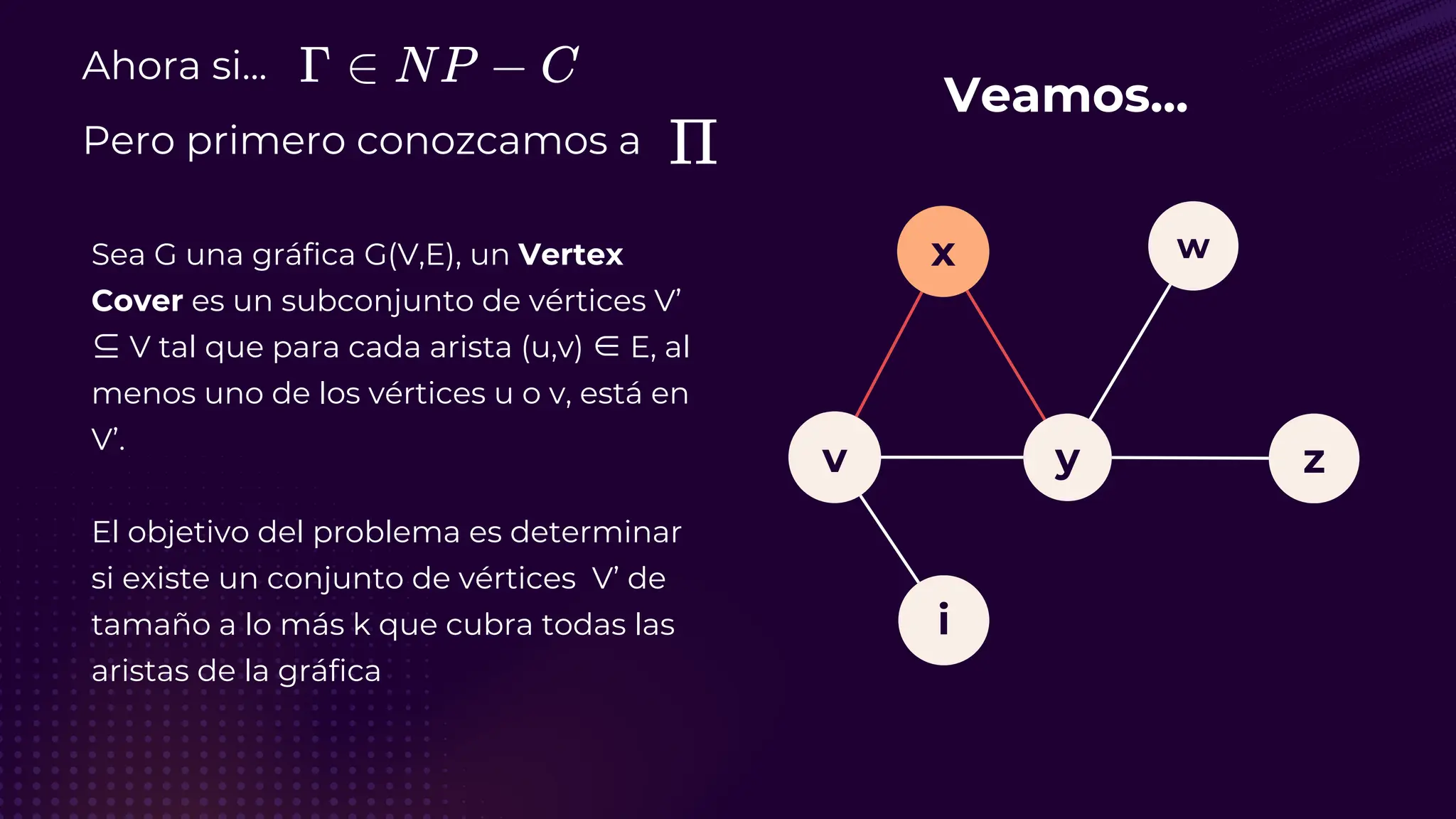
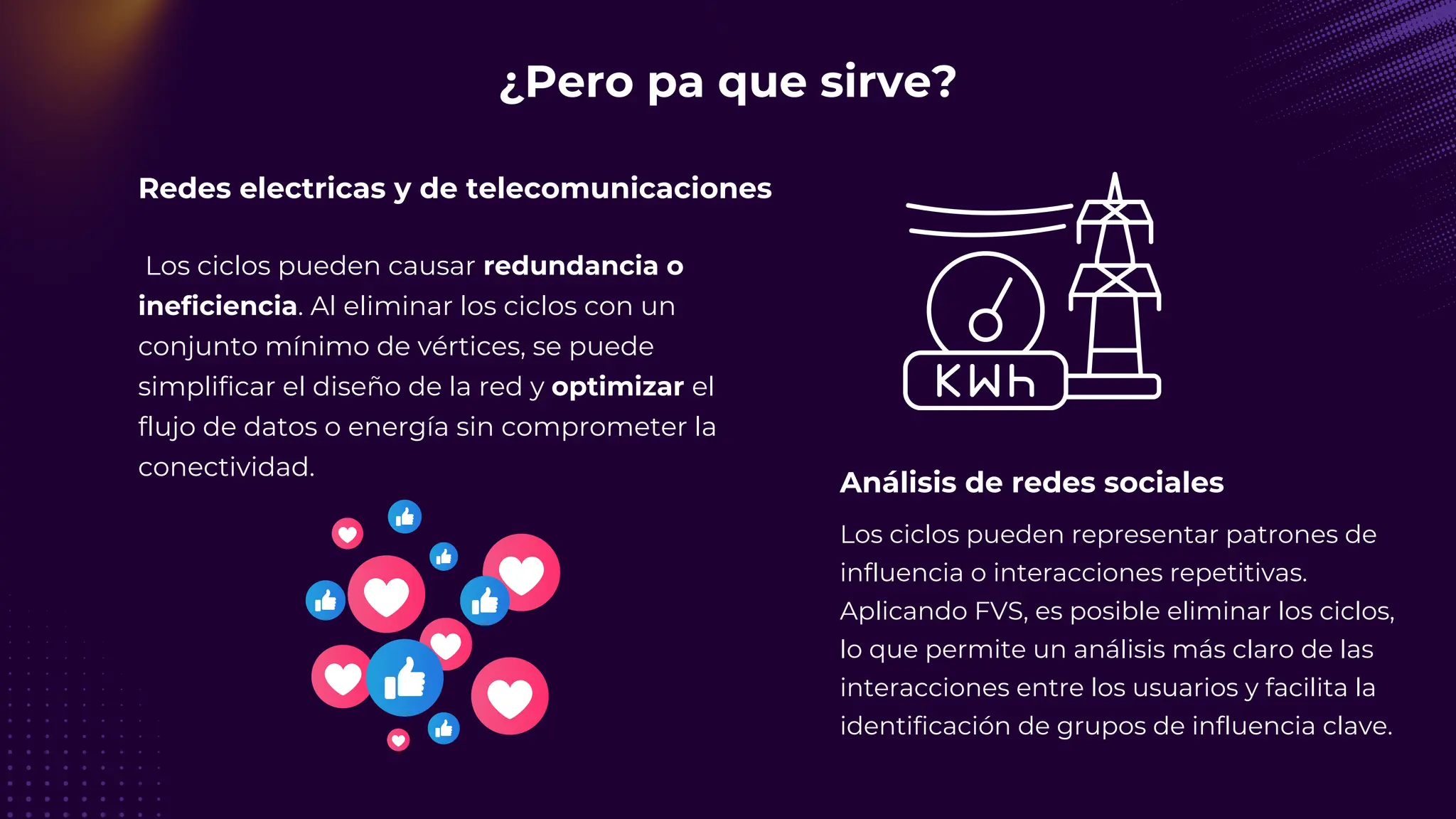
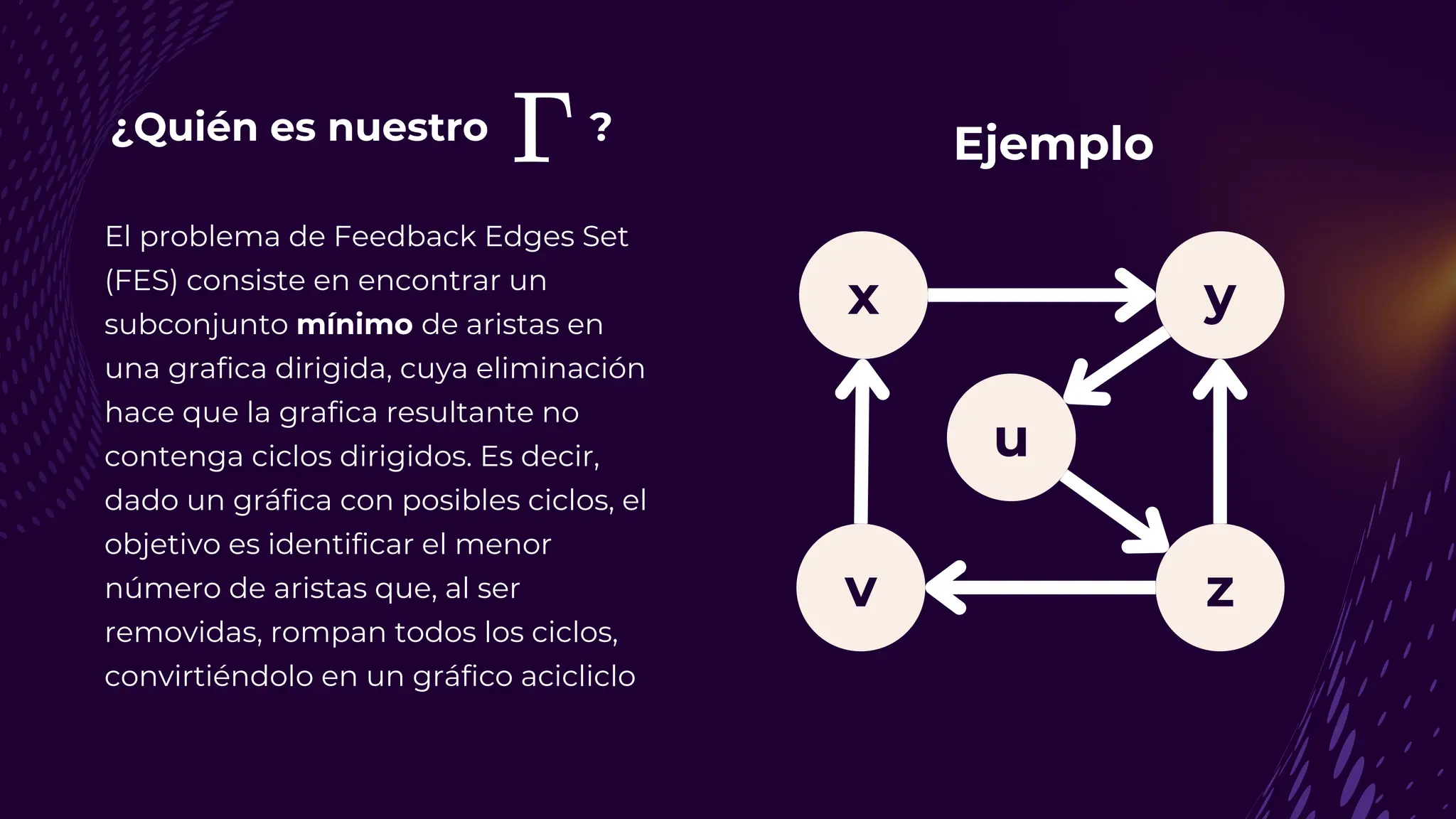
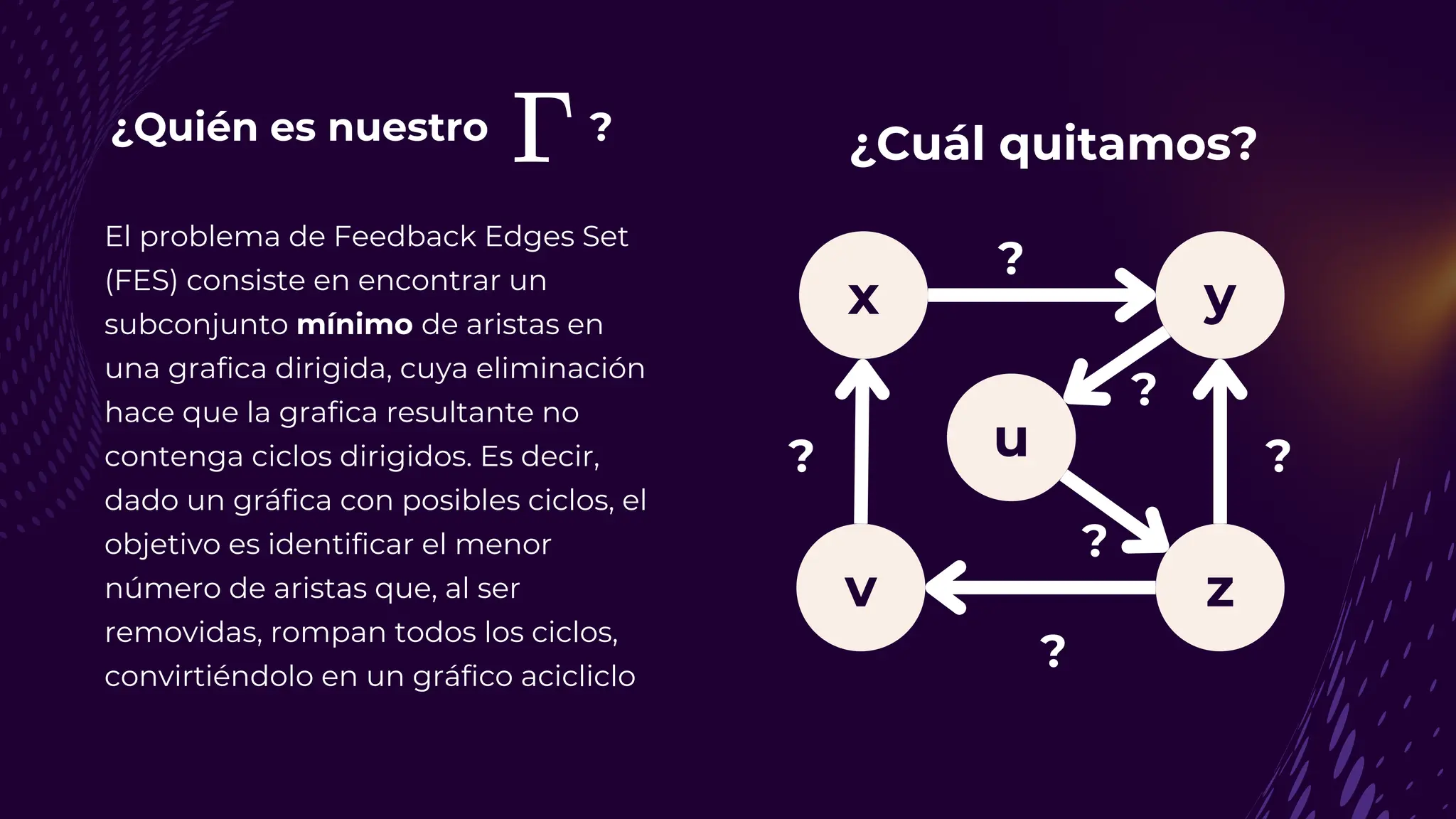
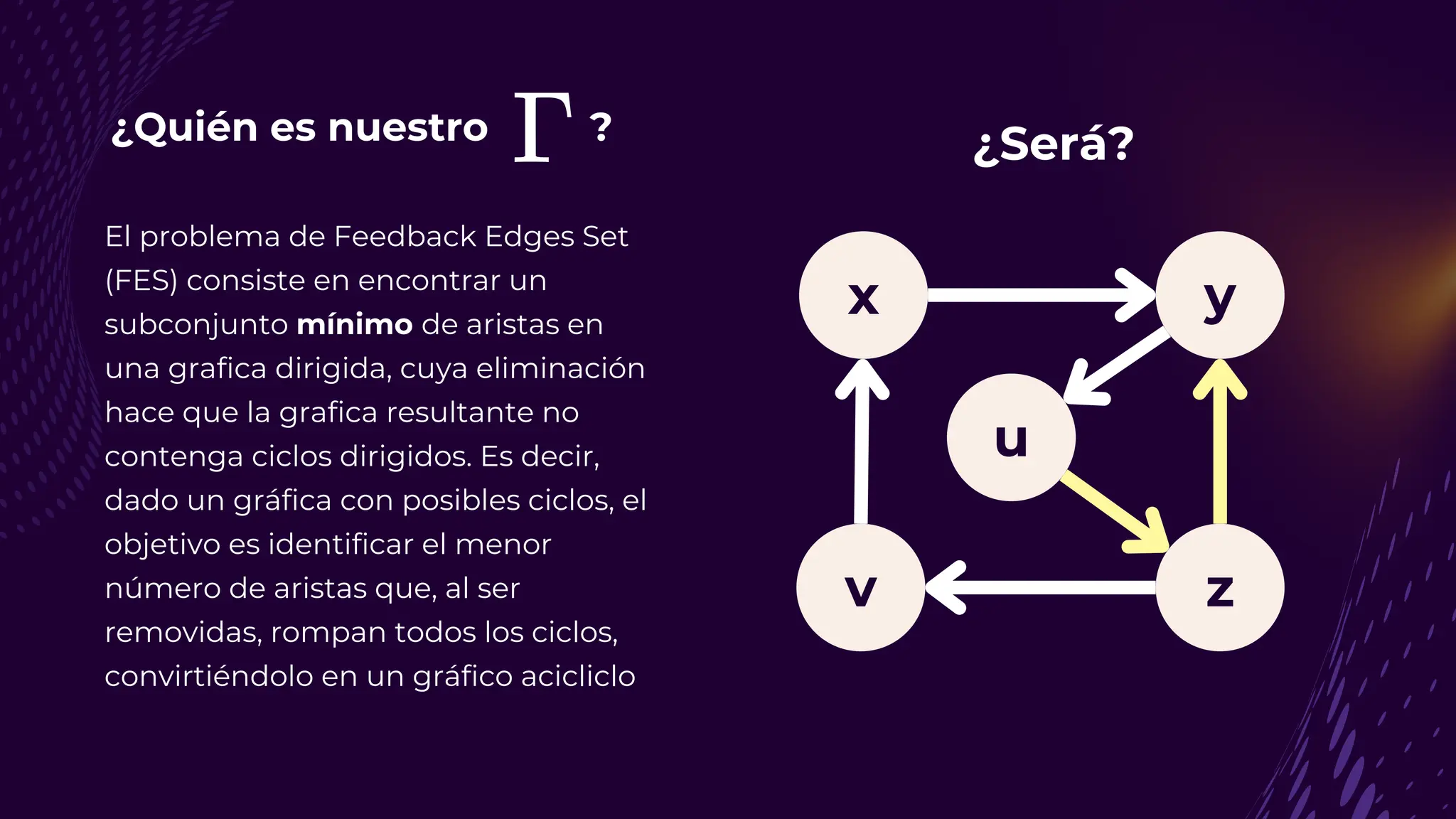
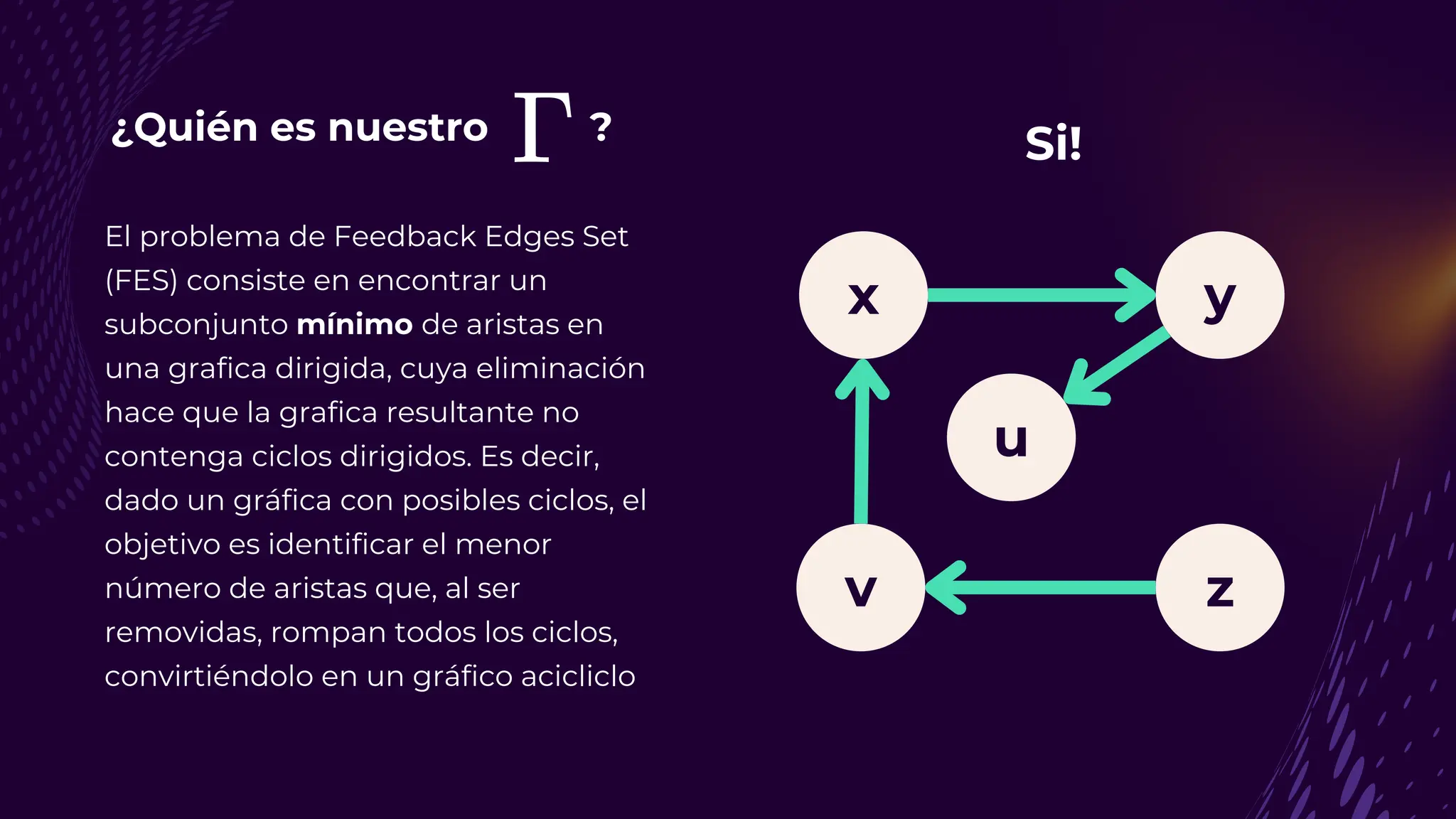
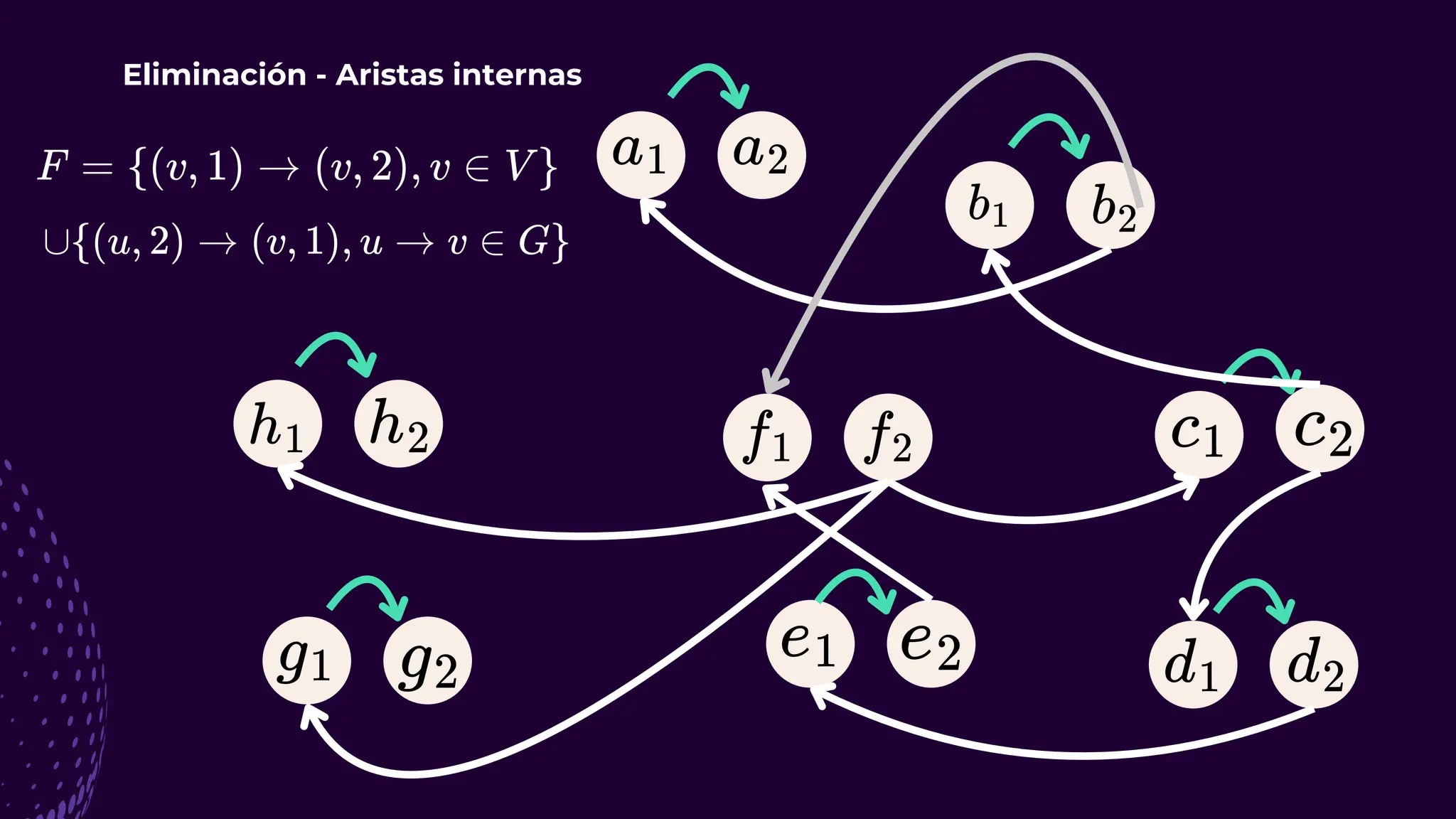
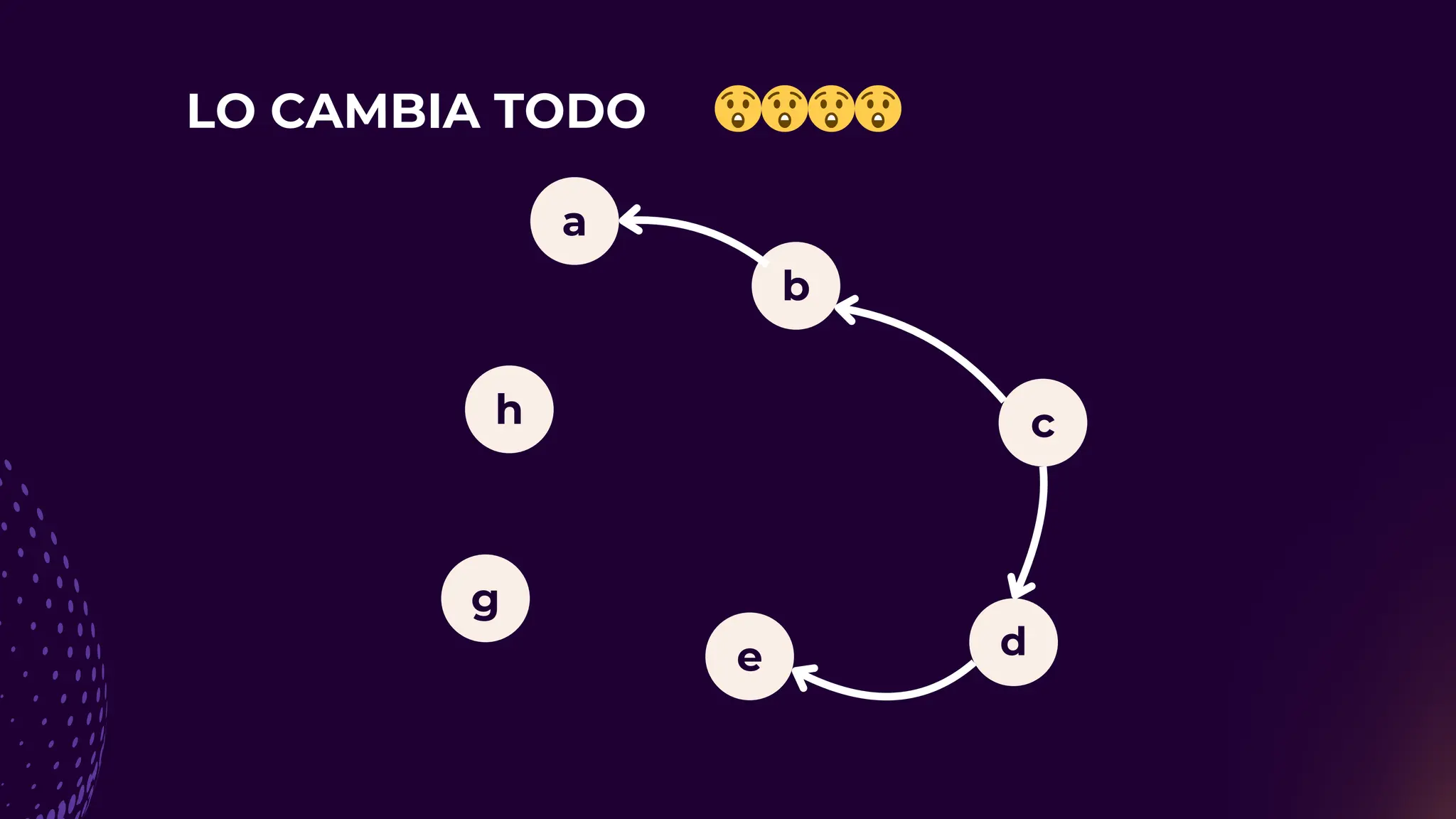
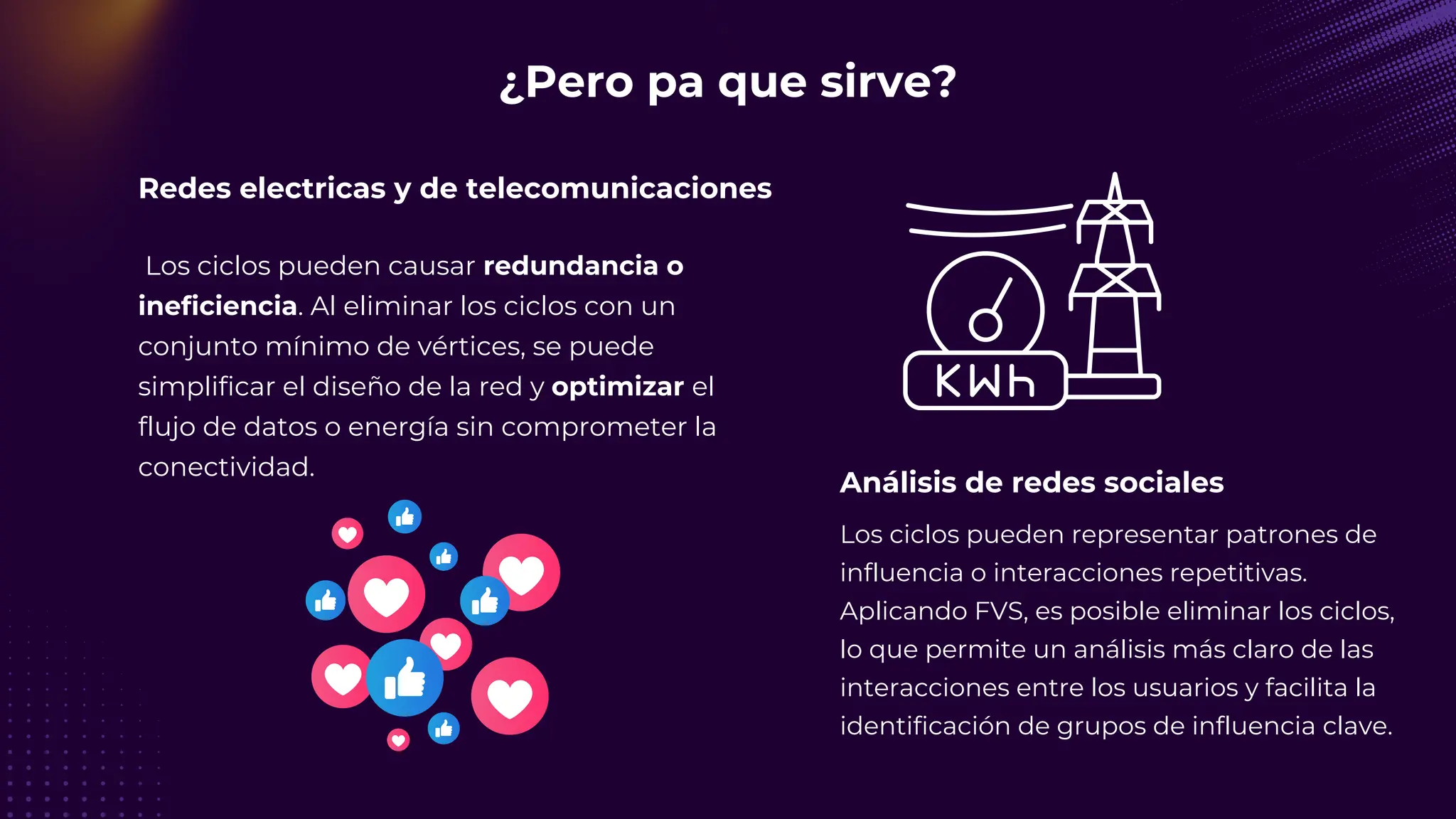
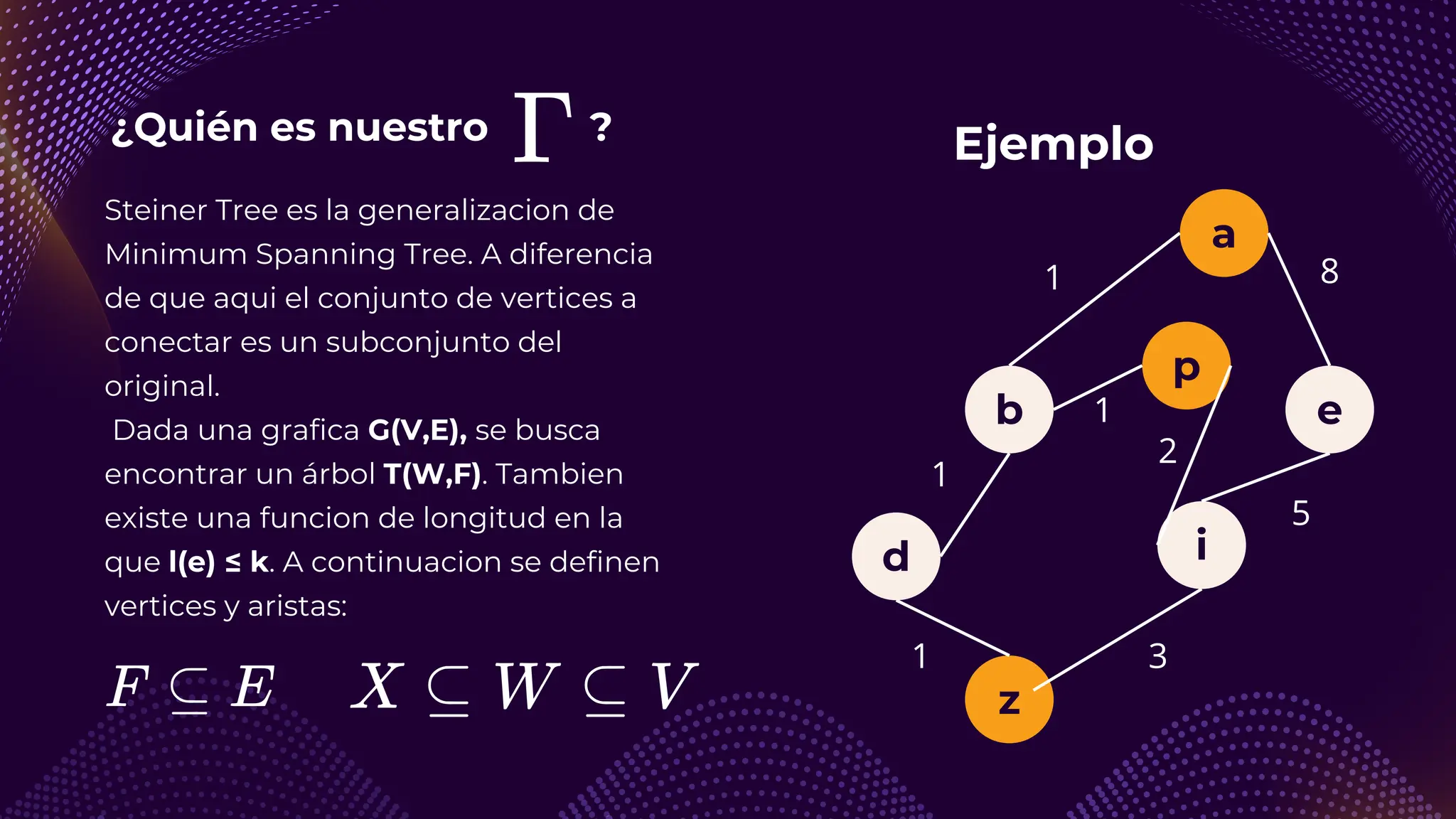
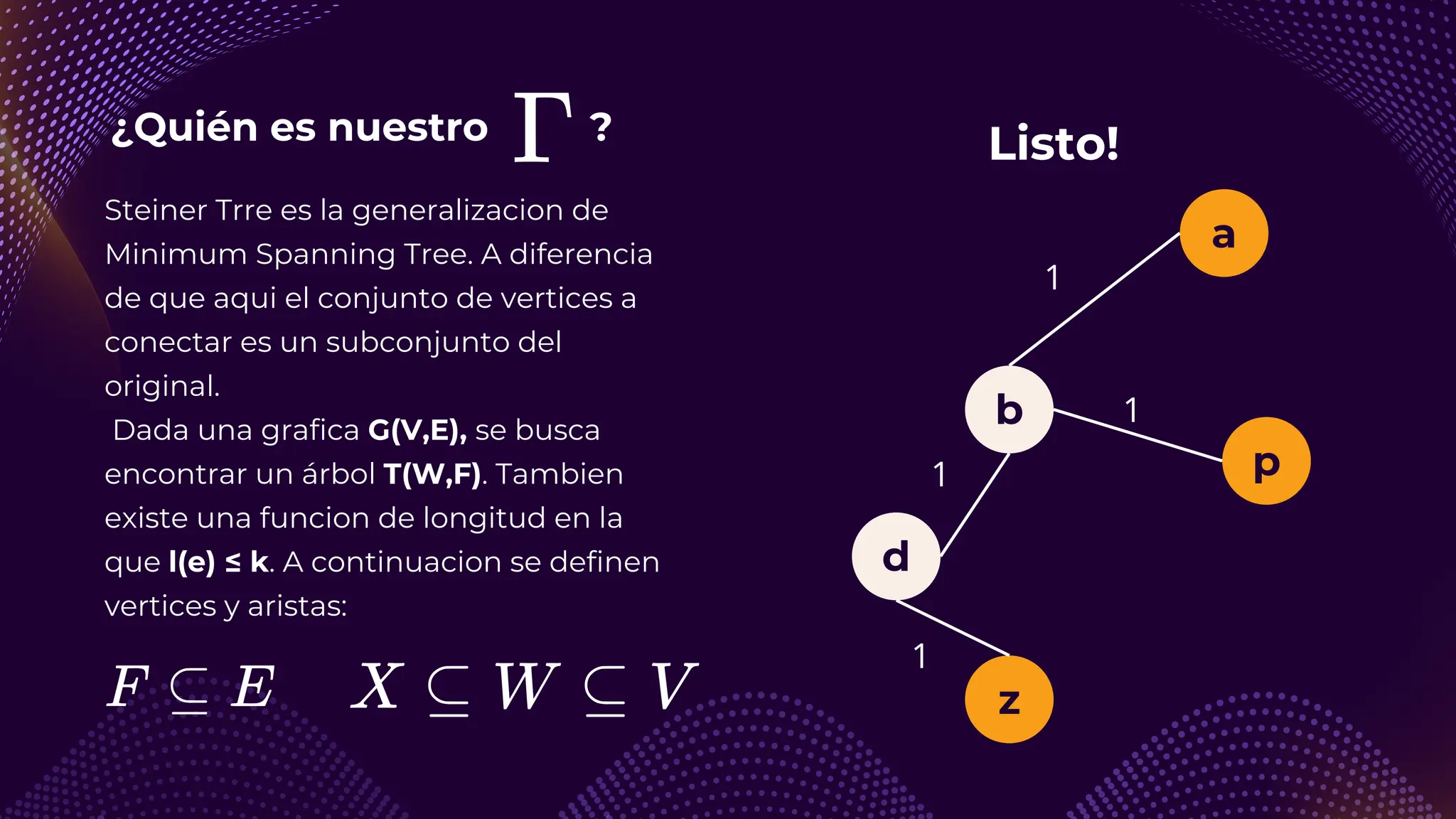
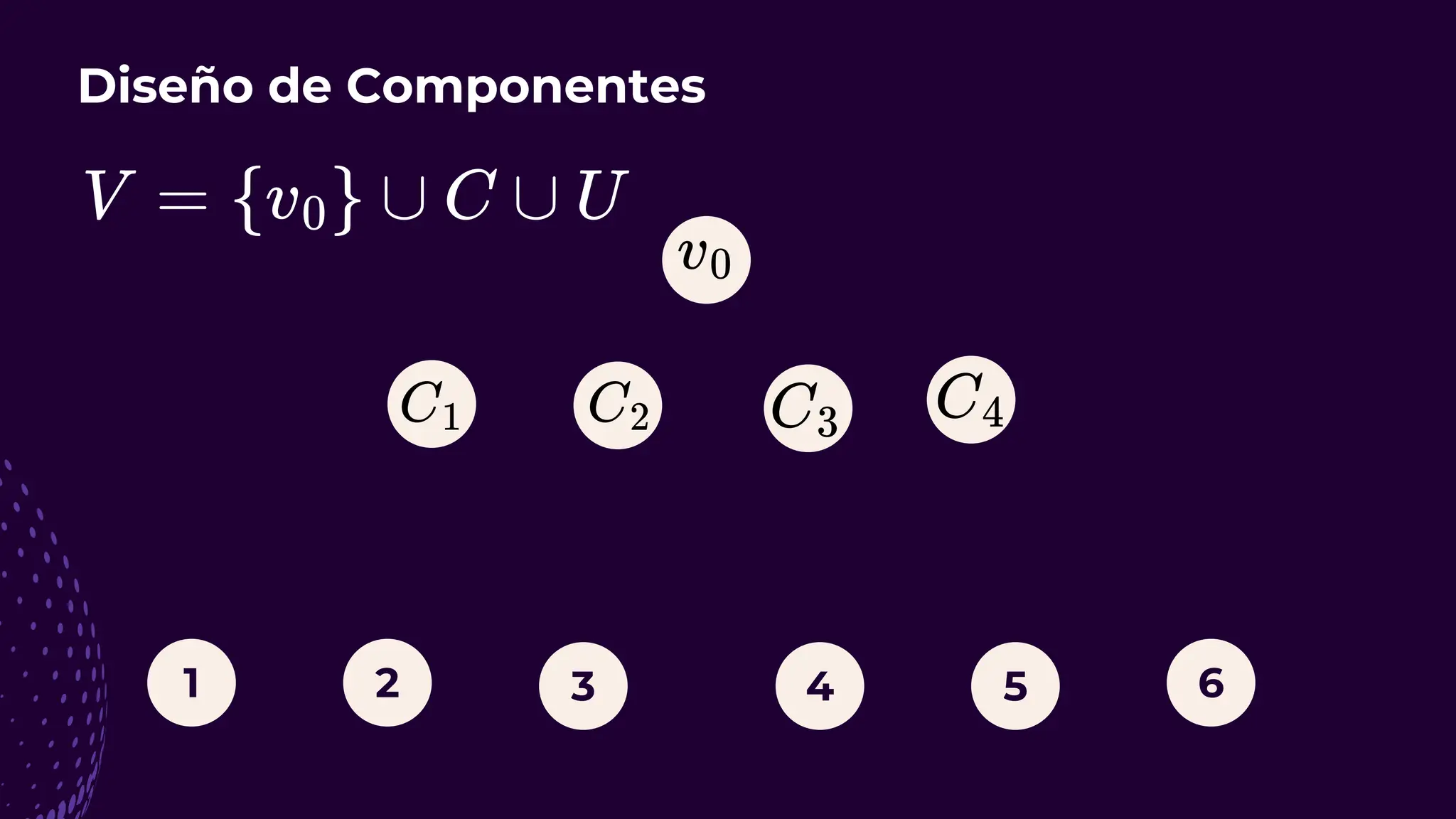
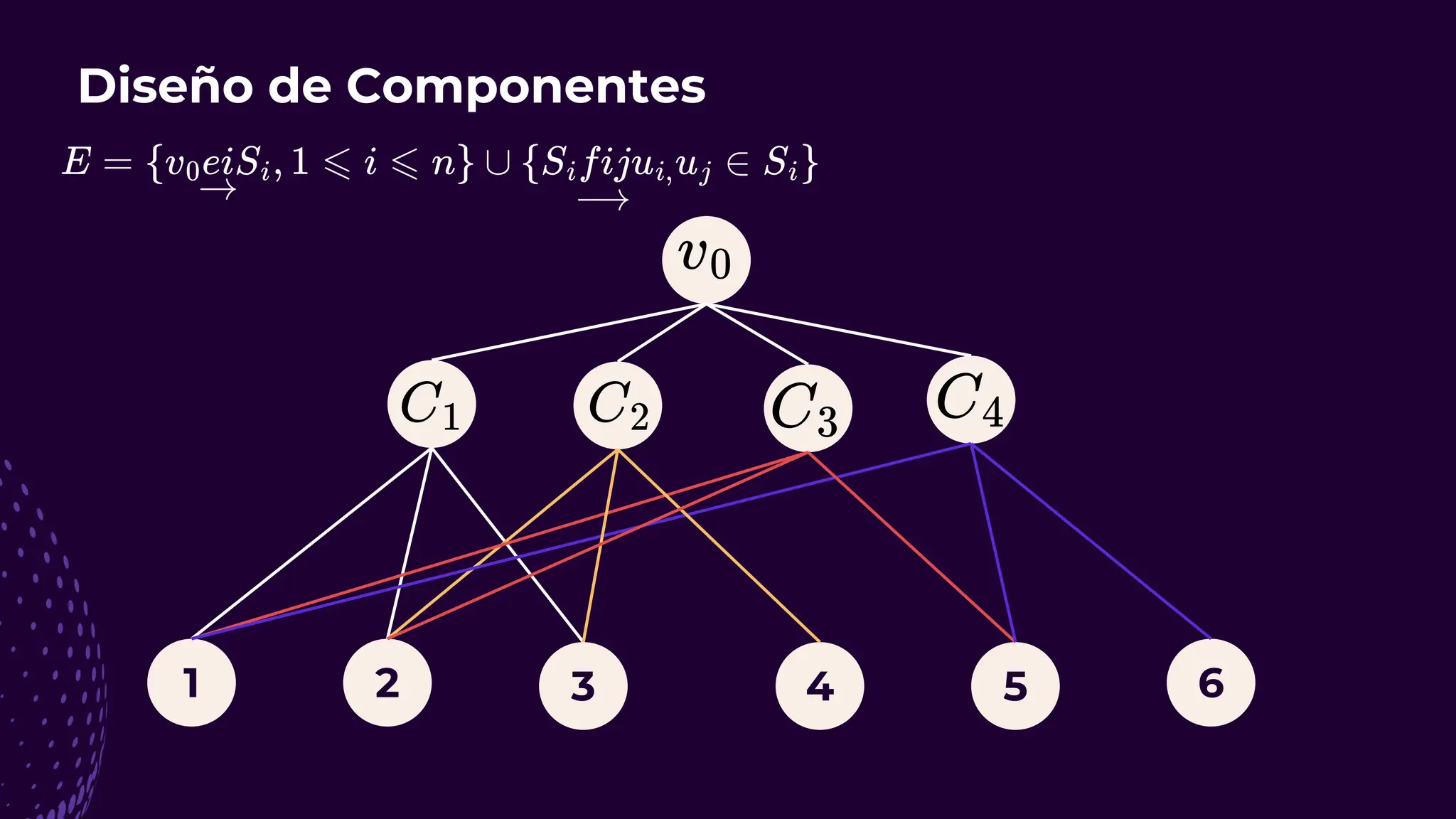
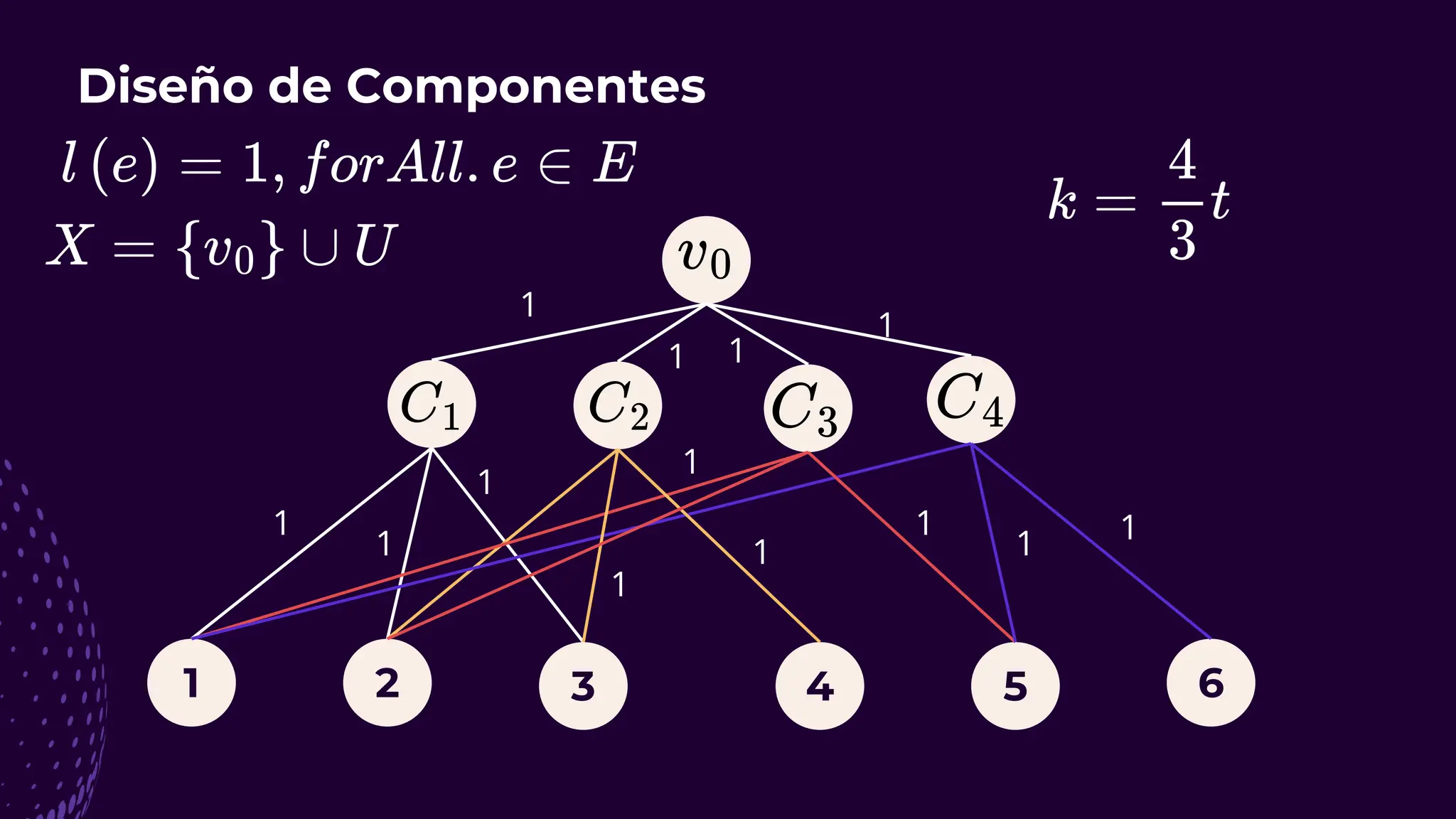
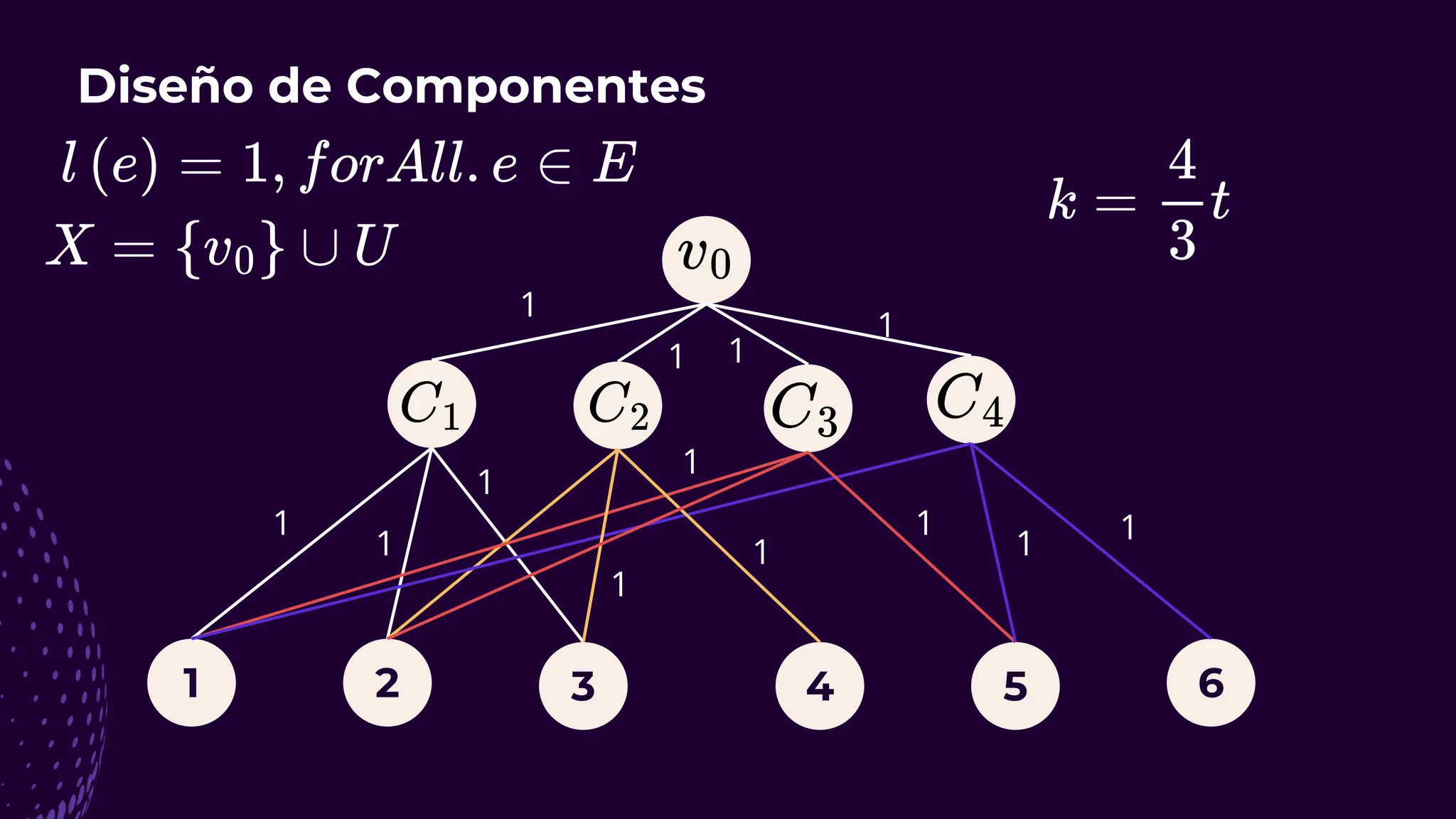
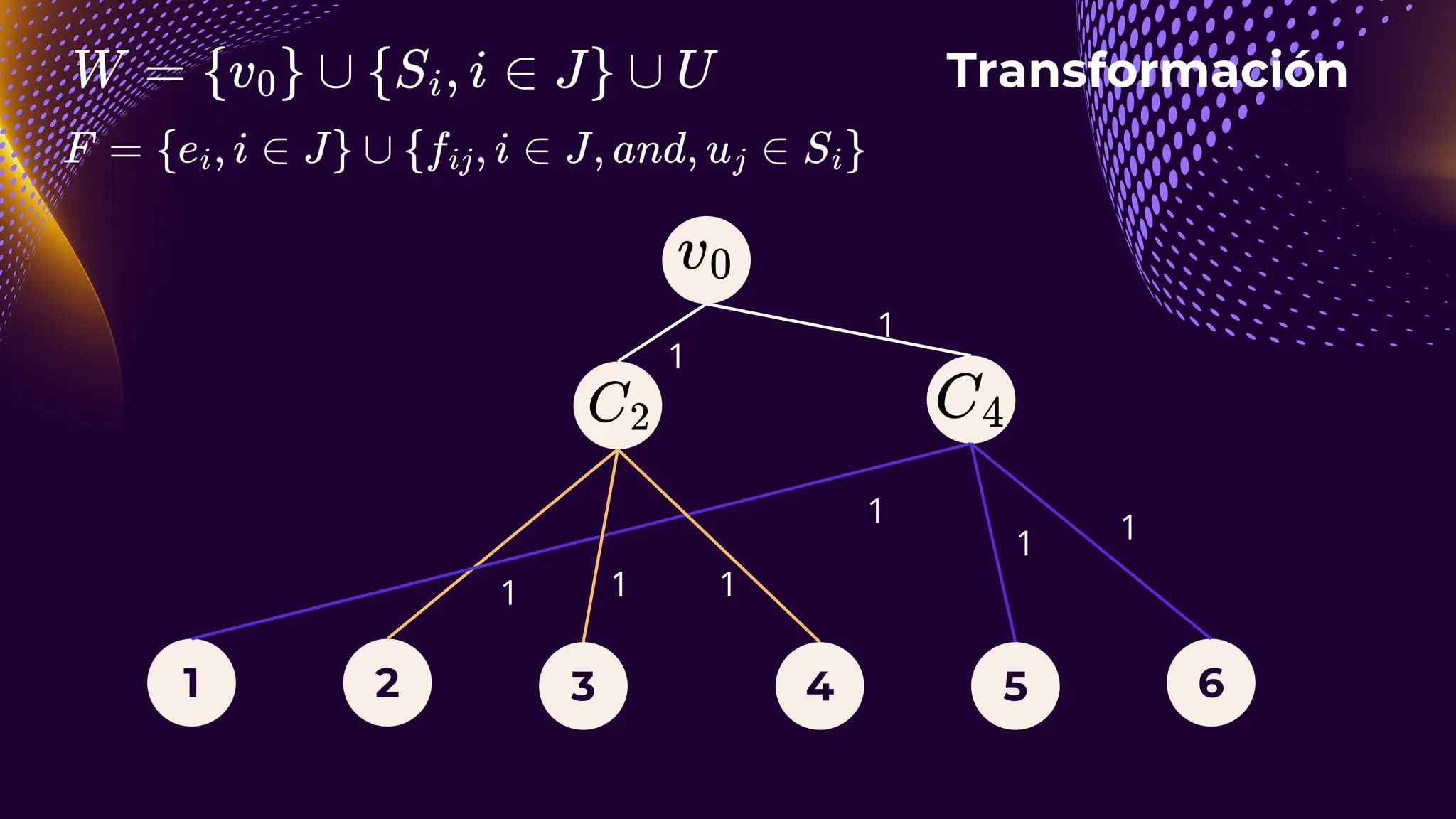
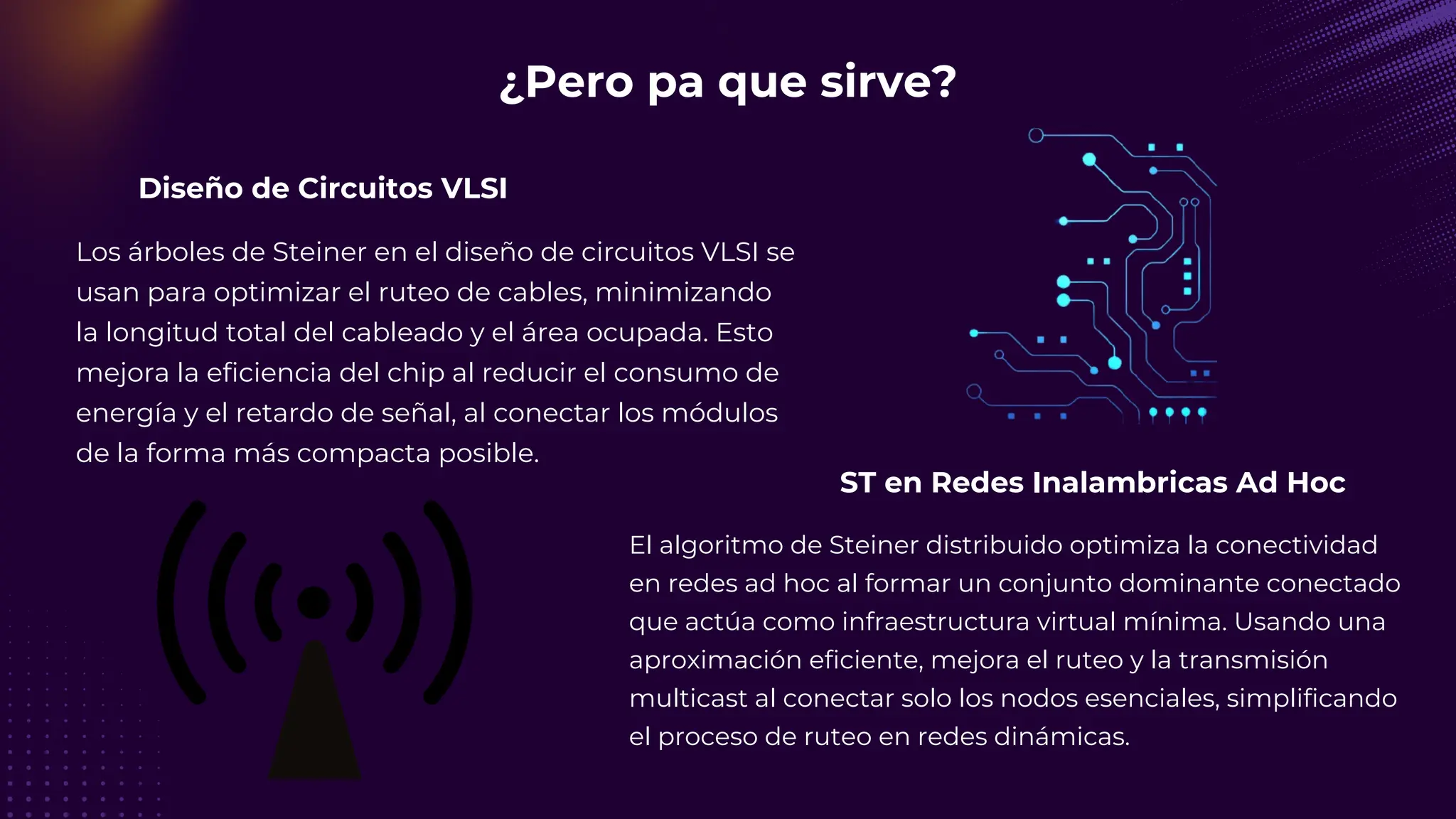
El documento discute el problema del conjunto de vértices de retroalimentación (FVS), que busca identificar el menor conjunto de vértices cuya eliminación de una gráfica dirigida elimina todos los ciclos dirigidos. También se aborda cómo se relaciona este problema con el conjunto de cobertura de vértices (VC) y se presenta un algoritmo no determinista para resolverlo, enfatizando su aplicabilidad en redes eléctricas y análisis de redes sociales. Finalmente, se menciona la relación entre FVS y el problema del árbol de Steiner, que busca encontrar un árbol de expansión mínimo entre un subconjunto de vértices.

1. FEEDBACK SETS IN DIGRAPHS
Mario Alberto Rocha Salazar

3. ¿Quién es nuestro ?
x
v z
x
El problema de Feedback Vertex Set
(FVS) consiste en dada una gráfica
G(V,E) encontrar un subconjunto
mínimo V’ de vértices en una gráfica
dirigida cuya eliminación haga que la
gráfica resultante no contenga ciclos
dirigidos. Es decir, dado un gráfica con
posibles ciclos, el objetivo es
identificar el menor número de
vértices que, al ser removidos, rompan
todos los ciclos convirtiéndolo en una
gráfica acíclica.
x
Ejemplo

4. ¿Quién es nuestro ?
y
v z
u
El problema de Feedback Vertex Set
(FVS) consiste en encontrar un
subconjunto mínimo de vértices en
una gráfica dirigida cuya eliminación
hace que la gráfica resultante no
contenga ciclos dirigidos. Es decir,
dado un gráfica con posibles ciclos, el
objetivo es identificar el menor
número de vértices que, al ser
removidos, rompan todos los ciclos
convirtiéndolo en una gráfica acíclica.
x
¿Cuál quitamos?

5. ¿Quién es nuestro ?
y
v z
u
El problema de Feedback Vertex Set
(FVS) consiste en encontrar un
subconjunto mínimo de vértices en
una gráfica dirigida cuya eliminación
hace que la gráfica resultante no
contenga ciclos dirigidos. Es decir,
dado un gráfica con posibles ciclos, el
objetivo es identificar el menor
número de vértices que, al ser
removidos, rompan todos los ciclos
convirtiéndolo en una gráfica acíclica.
x
¿Cuál quitamos?

6. ¿Quién es nuestro ?
v z
u
El problema de Feedback Vertex Set
(FVS) consiste en encontrar un
subconjunto mínimo de vértices en
una gráfica dirigida cuya eliminación
hace que la gráfica resultante no
contenga ciclos dirigidos. Es decir,
dado un gráfica con posibles ciclos, el
objetivo es identificar el menor
número de vértices que, al ser
removidos, rompan todos los ciclos
convirtiéndolo en una gráfica acíclica.
x
Listo!

7. FORMA CANÓNICA DE
¿Existe un subconjunto de vertices V´ en G
con | V´| ≤ k, tal que la gráfica resultante de
G al eliminar todos los vértices en V´ y sus
aristas incidentes sea acíclica?

8. El algoritmo no determinista
Fase Adivinadora Fase Verificadora
Tomamos en un vértice en V, tiramos
una moneda, si cae cara, lo
agregamos al conjunto V´. en
cualquier otro caso, no lo agregamos
y continuamos con todos los vertices.
ese será nuestro conjunto de
retroalimentación
Esta fase se ejecuta en tiempo
polinomial ya que el numero de
vértices que serán adivinados son
como máximo |V|.
Una vez que tenemos V’ ahora vamos
primero a verificar que |V’| ≤ k y
después vamos a eliminar cada
vertice en V y a sus aristas
incidentes de la gráfica original.
Ahora revisaremo si la gráfica
resultante es acíclicla.
Esto se puede hacer con algún
algoritmo que pueda detectar ciclos
en gráficas dirigidas como DFS que
sabemos que es de tiempo
polinomial
o(v+e)

9. Ahora si...
Pero primero conozcamos a
Sea G una gráfica G(V,E), un Vertex
Cover es un subconjunto de vértices V’
⊆ V tal que para cada arista (u,v) ∈ E, al
menos uno de los vértices u o v, está en
V’.
El objetivo del problema es determinar
si existe un conjunto de vértices V’ de
tamaño a lo más k que cubra todas las
aristas de la gráfica
Ejemplo
v
i
y
x
z
w

10. Ahora si...
Pero primero conozcamos a
Sea G una gráfica G(V,E), un Vertex
Cover es un subconjunto de vértices V’ ⊆
V tal que para cada arista (u,v) ∈ E, al
menos uno de los vértices u o v, está en
V’.
El objetivo del problema es determinar si
existe un conjunto de vértices V’ de
tamaño a lo más k que cubra todas las
aristas de la gráfica
¿Cuales elegimos?
v
i
y
x
z
w
? ?
?
?
?
?

11. Ahora si...
Pero primero conozcamos a
Sea G una gráfica G(V,E), un Vertex
Cover es un subconjunto de vértices V’
⊆ V tal que para cada arista (u,v) ∈ E, al
menos uno de los vértices u o v, está en
V’.
El objetivo del problema es determinar
si existe un conjunto de vértices V’ de
tamaño a lo más k que cubra todas las
aristas de la gráfica
¿Será?
v
i
y
x
z
w

12. v
i
y
x
z
w
Ahora si...
Pero primero conozcamos a
Sea G una gráfica G(V,E), un Vertex
Cover es un subconjunto de vértices V’
⊆ V tal que para cada arista (u,v) ∈ E, al
menos uno de los vértices u o v, está en
V’.
El objetivo del problema es determinar
si existe un conjunto de vértices V’ de
tamaño a lo más k que cubra todas las
aristas de la gráfica
Veamos...

13. Ahora si...
Pero primero conozcamos a
Sea G una gráfica G(V,E), un Vertex
Cover es un subconjunto de vértices V’
⊆ V tal que para cada arista (u,v) ∈ E, al
menos uno de los vértices u o v, está en
V’.
El objetivo del problema es determinar
si existe un conjunto de vértices V’ de
tamaño a lo más k que cubra todas las
aristas de la gráfica
Veamos...
v
i
y
x
z
w

14. Ahora si...
Pero primero conozcamos a
Sea G una gráfica G(V,E), un Vertex
Cover es un subconjunto de vértices V’
⊆ V tal que para cada arista (u,v) ∈ E, al
menos uno de los vértices u o v, está en
V’.
El objetivo del problema es determinar
si existe un conjunto de vértices V’ de
tamaño a lo más k que cubra todas las
aristas de la gráfica
Veamos...
v
i
y
x
z
w

15. Ahora si...
Pero primero conozcamos a
Sea G una gráfica G(V,E), un Vertex
Cover es un subconjunto de vértices V’
⊆ V tal que para cada arista (u,v) ∈ E, al
menos uno de los vértices u o v, está en
V’.
El objetivo del problema es determinar
si existe un conjunto de vértices V’ de
tamaño a lo más k que cubra todas las
aristas de la gráfica
Si es VC
v
i
y
x
z
w

16. FORMA CANÓNICA DE
¿Existe un subconjunto de vertices V´ con
| V´| ≤ k, tal que cada arista (u,v) incide en al
menos un vertice en V’?

17. AHORA SI...
Proponemos a f como:
in E }
Para cada arista en nuestra gafica en π. Para
Γ se crearán 2 aristas a -> b y b -> a
generando un ciclo a -> b -> a.
Nota: Los vertices serán los mismos.

18. Pero... ¿por que funciona?
Vemos que para cada arista en
la gráfica original, en nuestra
grafica en Γ se agregan dos
aristas dirigidas
Construyamos un Ejemplo
Tenemos el siguente VC en G
a
b
c
f
h
g
e d

19. Pero... ¿por que funciona?
Vemos que para cada arista en
la gráfica original, en nuestra
gráfica de Γ se agregan dos
aristas dirigidas
Construyamos un Ejemplo
a
b
c
f
h
g
e d

20. Pero... ¿por que funciona?
Se establece una relación entre VC y FVS
veamos:
Para VC: necesitamos un conjunto mínimo
tal que cada arista este cubierta es decir, al
menos uno de los extremos de cada arista
debe pertenece a ese conjunto.
Para FVS: Necesitamos un conjunto de
vértices minimo tal que si los eliminamos en
la grafica, resulta en una gráfica sin ciclos
dirigidos.
a
b
c
f
h
g
e d
Construyamos un Ejemplo

21. a
b
c
f
h
g
e d
Pero... ¿por que funciona?
Ahora, dado que cada arista en G de VC se
transforma en dos aristas dirigidas en H en
FVS, formando un ciclo dirigido, entonces el
conjunto V’ debe incluir al menos uno de los
vértices para romper ese ciclo
Si tenemos V’ en VC en G, entonces V’ debe
cubrir cada arista en G, eso significa que para
cada ciclo dirigido correspondiente en H, V’
debe contener al menos uno de los vértices en
ese ciclo para romperlo.
Al eliminar V’ en H todos los ciclos dirigidos se
eliminan lo que hace que H sea acíclico.
Construyamos un Ejemplo

22. a
b
c
f
h
g
e d
Pero... ¿por que funciona?
Ahora, dado que cada arista en G de VC se
transforma en dos aristas dirigidas en H en
FVS, formando un ciclo dirigido, entonces el
conjunto V’ debe incluir al menos uno de los
vértices para romper ese ciclo
Si tenemos V’ en VC en G, entonces V’ debe
cubrir cada arista en G, eso significa que para
cada ciclo dirigido correspondiente en H, V’
debe contener al menos uno de los vértices en
ese ciclo para romperlo.
Al eliminar V’ en H todos los ciclos dirigidos se
eliminan lo que hace que H sea acíclico.
Construyamos un Ejemplo

23. a
c
h
g
e
Pero... ¿por que funciona?
Ahora, dado que cada arista en G de VC se
transforma en dos aristas dirigidas en H en
FVS, formando un ciclo dirigido, entonces el
conjunto V’ debe incluir al menos uno de los
vértices para romper ese ciclo
Si tenemos V’ en VC en G, entonces V’ debe
cubrir cada arista en G, eso significa que para
cada ciclo dirigido correspondiente en H, V’
debe contener al menos uno de los vértices en
ese ciclo para romperlo.
Al eliminar V’ en H todos los ciclos dirigidos se
eliminan lo que hace que H sea acíclico.
Construyamos un Ejemplo

24. ¿Qué técnica se usó?
Reemplazo
¿Por qué?
transformamos el ejemplar de un problema
en otra manteniendo las propiedades
esenciales. En el caso de FVS, se reduce el
problema de Vertex Cover al de Feedback
Vertex Set mediante una transformación en
la que los vértices y aristas del problema
original se reemplazan localmente en un
nueva gráfica, conservando su estructura
esencial.

25. Redes electricas y de telecomunicaciones
¿Pero pa que sirve?
Los ciclos pueden causar redundancia o
ineficiencia. Al eliminar los ciclos con un
conjunto mínimo de vértices, se puede
simplificar el diseño de la red y optimizar el
flujo de datos o energía sin comprometer la
conectividad.
Análisis de redes sociales
Los ciclos pueden representar patrones de
influencia o interacciones repetitivas.
Aplicando FVS, es posible eliminar los ciclos,
lo que permite un análisis más claro de las
interacciones entre los usuarios y facilita la
identificación de grupos de influencia clave.

26. Ahora...

28. ¿Quién es nuestro ?
El problema de Feedback Edges Set
(FES) consiste en encontrar un
subconjunto mínimo de aristas en
una grafica dirigida, cuya eliminación
hace que la grafica resultante no
contenga ciclos dirigidos. Es decir,
dado un gráfica con posibles ciclos, el
objetivo es identificar el menor
número de aristas que, al ser
removidas, rompan todos los ciclos,
convirtiéndolo en un gráfico acicliclo
y
v z
u
x
Ejemplo

29. ¿Quién es nuestro ?
El problema de Feedback Edges Set
(FES) consiste en encontrar un
subconjunto mínimo de aristas en
una grafica dirigida, cuya eliminación
hace que la grafica resultante no
contenga ciclos dirigidos. Es decir,
dado un gráfica con posibles ciclos, el
objetivo es identificar el menor
número de aristas que, al ser
removidas, rompan todos los ciclos,
convirtiéndolo en un gráfico acicliclo
y
v z
u
x
¿Cuál quitamos?
?
?
?
?
?
?

30. ¿Quién es nuestro ?
El problema de Feedback Edges Set
(FES) consiste en encontrar un
subconjunto mínimo de aristas en
una grafica dirigida, cuya eliminación
hace que la grafica resultante no
contenga ciclos dirigidos. Es decir,
dado un gráfica con posibles ciclos, el
objetivo es identificar el menor
número de aristas que, al ser
removidas, rompan todos los ciclos,
convirtiéndolo en un gráfico acicliclo
y
v z
u
x
¿Será?

31. ¿Quién es nuestro ?
El problema de Feedback Edges Set
(FES) consiste en encontrar un
subconjunto mínimo de aristas en
una grafica dirigida, cuya eliminación
hace que la grafica resultante no
contenga ciclos dirigidos. Es decir,
dado un gráfica con posibles ciclos, el
objetivo es identificar el menor
número de aristas que, al ser
removidas, rompan todos los ciclos,
convirtiéndolo en un gráfico acicliclo
y
v z
u
x
Si!

32. FORMA CANÓNICA DE
¿Existe un subconjunto de aristas E´ en G con
| E´| ≤ k, tal que la gráfica resultante de G al
eliminar todas las aristas en E´ sea acíclica?

33. El algoritmo no determinista
Fase Adivinadora Fase Verificadora
Tomamos una arista en E, tiramos
una moneda, si cae cara lo
agregamos a E’ en cualquier otro
caso no la agregamos y continuamos
asi con todas las aristas de E.
Esta fase se ejecuta en tiempo
polinomial ya que el numero de
aristas que serán adivinados son
como máximo |E|.
Una vez que tenemos E’ ahora vamos
primero a verificar que |E| ≤ k y
después vamos a eliminar cada arista
en E y Ahora revisaremos si la gráfica
resultante es acíclicla.
Esto se puede hacer con algún
algoritmo que pueda detectar ciclos
en gráficas dirigidas como DFS que
sabemos que es de tiempo
polinomial

34. Espera... Ya lo conocemos!
Ahora si...
Pero primero conozcamos a

35. Para demostrar que NP-C
ocuparemos como
a FVS
Ahora si...
Pero primero conozcamos a

36. AHORA SI...
Proponemos a f como:
in G}
Para cada vertice en G, se duplicará en H, y para las
aristas tendremos 2 formas de construirlas, las aristas
externas y las internas.

37. Pero... ¿por que funciona?
Cada vértice en G se duplica en H, creando dos copias de vértices y las aristas de la gráfica
original se dividen en aristas internas (entre las dos copias de un mismo vértice) y aristas
externas (entre copias de vértices diferentes).
Al resolver FES en H, buscamos un conjunto de aristas que rompa todos los ciclos en H. La
clave está en que todos los ciclos que involucran aristas externas también pasan por aristas
internas, por lo que eliminar solo aristas internas (que corresponden a vértices en G) es
suficiente para romper los ciclos.
Por lo tanto, cualquier conjunto de aristas internas que forme una solución para FES en H
corresponde a un conjunto de vértices que forman una solución para FVS en G. De esta
forma, resolver FES en la gráfica transformada es lo mismo que resolver FVS en la gráfica
original, ya que los ciclos que rompes en H corresponden directamente a los ciclos que
romperías en G.

38. Pero... ¿por que funciona?
a
b
c
f
h
g
e d

39. Transformacion - Duplicamos vértices

40. Transformacion - Aristas internas

41. Transformacion - Aristas externas

42. Eliminación - Aristas internas

43. LO CAMBIA TODO
a
b
c
h
g
e d
😲😲😲😲

44. ¿Qué técnica se usó?
Los elementos del ejemplar original
(vértices y aristas) se remplazan por un
conjunto equivalente en el nuevo
problema, donde los ciclos en la gráfica
dirigida son reemplazados por las aristas
que se deben eliminar para romper esos
ciclos.
Este reemplazo directo transforma las
aristas de Vertex Cover en aristas dirigidas
en FES, y resolver el problema de cubrir
aristas se convierte en eliminar aristas que
rompan los ciclos.
¿Por qué?
Reemplazo Local

45. Redes electricas y de telecomunicaciones
¿Pero pa que sirve?
Los ciclos pueden causar redundancia o
ineficiencia. Al eliminar los ciclos con un
conjunto mínimo de vértices, se puede
simplificar el diseño de la red y optimizar el
flujo de datos o energía sin comprometer la
conectividad.
Análisis de redes sociales
Los ciclos pueden representar patrones de
influencia o interacciones repetitivas.
Aplicando FVS, es posible eliminar los ciclos,
lo que permite un análisis más claro de las
interacciones entre los usuarios y facilita la
identificación de grupos de influencia clave.

46. Y por ultimo...

48. ¿Quién es nuestro ?
Steiner Tree es la generalizacion de
Minimum Spanning Tree. A diferencia
de que aqui el conjunto de vertices a
conectar es un subconjunto del
original.
Dada una grafica G(V,E), se busca
encontrar un árbol T(W,F). Tambien
existe una funcion de longitud en la
que l(e) ≤ k. A continuacion se definen
vertices y aristas:
Ejemplo
a
b e
i
z
d
1
1
1
p
8
5
3
1
2

49. ¿Quién es nuestro ?
a
b
z
d
1
1
1
p
1
Steiner Trre es la generalizacion de
Minimum Spanning Tree. A diferencia
de que aqui el conjunto de vertices a
conectar es un subconjunto del
original.
Dada una grafica G(V,E), se busca
encontrar un árbol T(W,F). Tambien
existe una funcion de longitud en la
que l(e) ≤ k. A continuacion se definen
vertices y aristas:
Listo!

50. FORMA CANÓNICA DE
¿Existe un arbol T(W,F) en G, tal que
?
y

51. El algoritmo no determinista
Fase Adivinadora Fase Verificadora
Tomamos un vértice de V, tiramos
una moneda, si cae cara la
agregamos al conjunto X en
cualquier otro caso no la agregamos ,
continuamos asi para todos los
vértices en la gráfica G.
para las aristas tomamos una arista
de E, tiramos una moneda, si cae
cara la agregamos al conjunto E’ en
cualquier otro caso no la agregamos ,
continuamos asi para todas las
aristas en la gráfica G.
Una vez que se ha adivinado el
subconjunto X de vértices y E′ de
aristas, debemos comprobar que:
X incluye todos los vértices
terminales.
1.
E’ forma un árbol que conecta
todos los vértices en X′.
2.
Verificamos que la suma del
costo de cada arista es menor a k
3.

52. Ahora si...
Pero primero conozcamos a
Dado un conjunto U, tal que |U| = 3q, y
una colección C de subconjuntos de
tamaño 3 de U. El objetivo es
determinar si existe un subcojunto C’
3XC
en el que ademas cada elemento de U
aparezca exactamente una vez en un
subconjunto de C’
¿Existe C’?

53. Ahora si...
Pero primero conozcamos a
Dado un conjunto U, tal que |U| = 3q, y
una colección C de subconjuntos de
tamaño 3 de U. El objetivo es
determinar si existe un subcojunto C’
3XC
en el que ademas cada elemento de U
aparezca exactamente una vez en un
subconjunto de C’

54. FORMA CANÓNICA DE
¿Existe un subconjunto tal que
cada elemento de U aparece exactamente
una sola vez en los subconjuntos de C’?

55. AHORA SI...
Proponemos a f como:
Pero primero diseñaremos componentes en un
ejemplar del problema para después aplicar la
transformación

56. Diseño de Componentes

57. Diseño de Componentes

58. 1 2 4 5 6
3
Diseño de Componentes

59. 1 2 4 5 6
3
Diseño de Componentes

60. 1 2 4 5 6
3
1
1
1
1
1
1
1
1 1
1
1
1
1
Diseño de Componentes

61. 1 2 4 5 6
3
1
1
1
1
1
1
1
1 1
1
1
1
1
Diseño de Componentes

62. Transformación
1 2 4 5 6
3
1
1 1
1 1
1
1
1

63. Transformación
Obteniendo el valor de k, nos damos
cuienta que se ha obtenido una relacion de
1 a 1 tal como lo requiere la estructura de
3XC. En la que se ha encontrado una
cobertura de U a la vez de un árbol de
Steiner en la que W = {1,2,3,4,5,6,C2,C4,v0}

64. ¿Qué técnica se usó?
Diseño de
Componentes
¿Por qué?
Los elementos de 3XC no son directamente
mapeables al problema ST, por lo que se
descumposo atomicamente cada uno de
los elementos en 3XC, obteniendo
componentes (vertices y aristas) e
integrandolos de tal forma que la esencia
de ST se mantenga al realizar la reducción

65. Diseño de Circuitos VLSI
¿Pero pa que sirve?
Los árboles de Steiner en el diseño de circuitos VLSI se
usan para optimizar el ruteo de cables, minimizando
la longitud total del cableado y el área ocupada. Esto
mejora la eficiencia del chip al reducir el consumo de
energía y el retardo de señal, al conectar los módulos
de la forma más compacta posible.
ST en Redes Inalambricas Ad Hoc
El algoritmo de Steiner distribuido optimiza la conectividad
en redes ad hoc al formar un conjunto dominante conectado
que actúa como infraestructura virtual mínima. Usando una
aproximación eficiente, mejora el ruteo y la transmisión
multicast al conectar solo los nodos esenciales, simplificando
el proceso de ruteo en redes dinámicas.

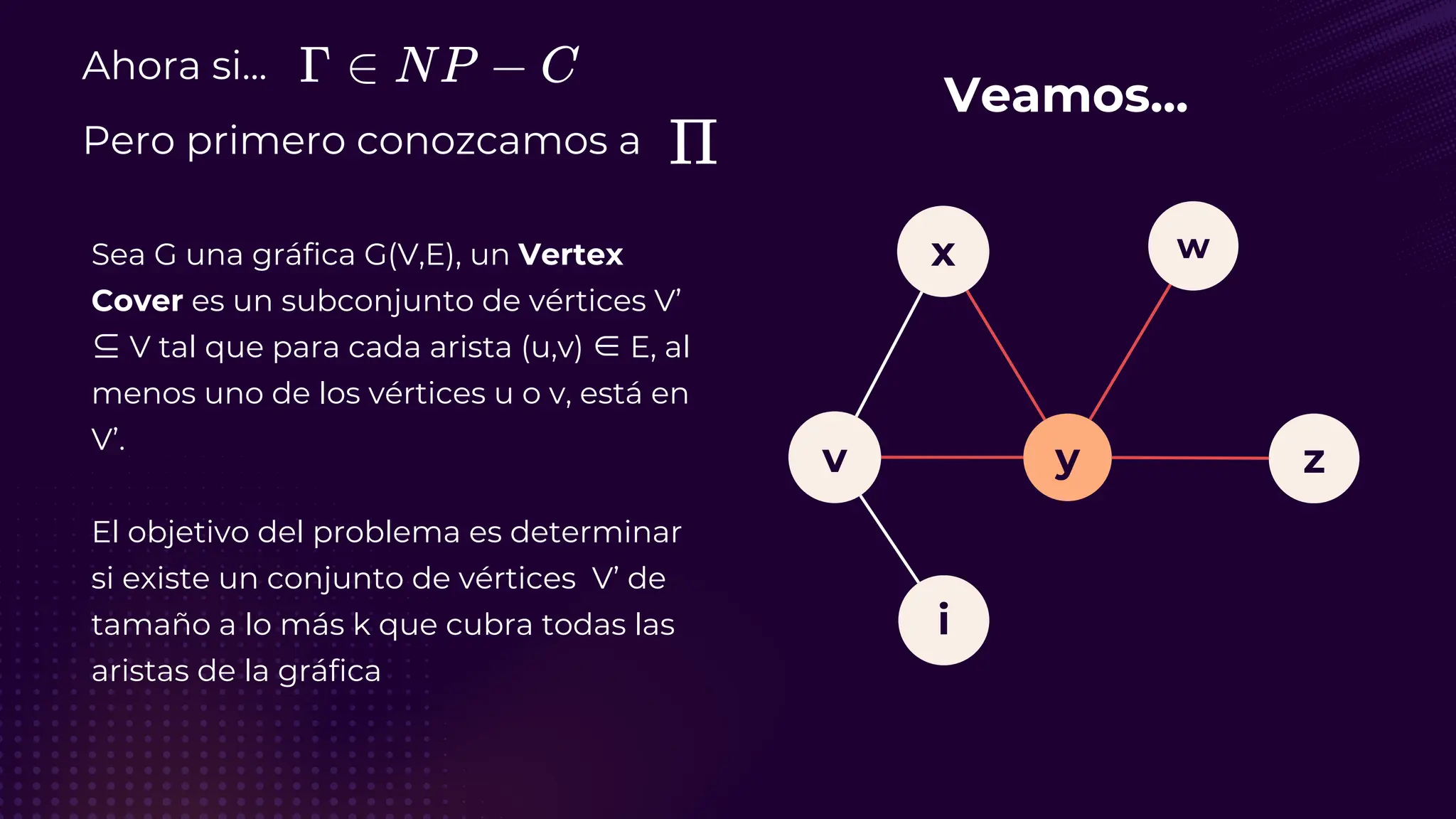
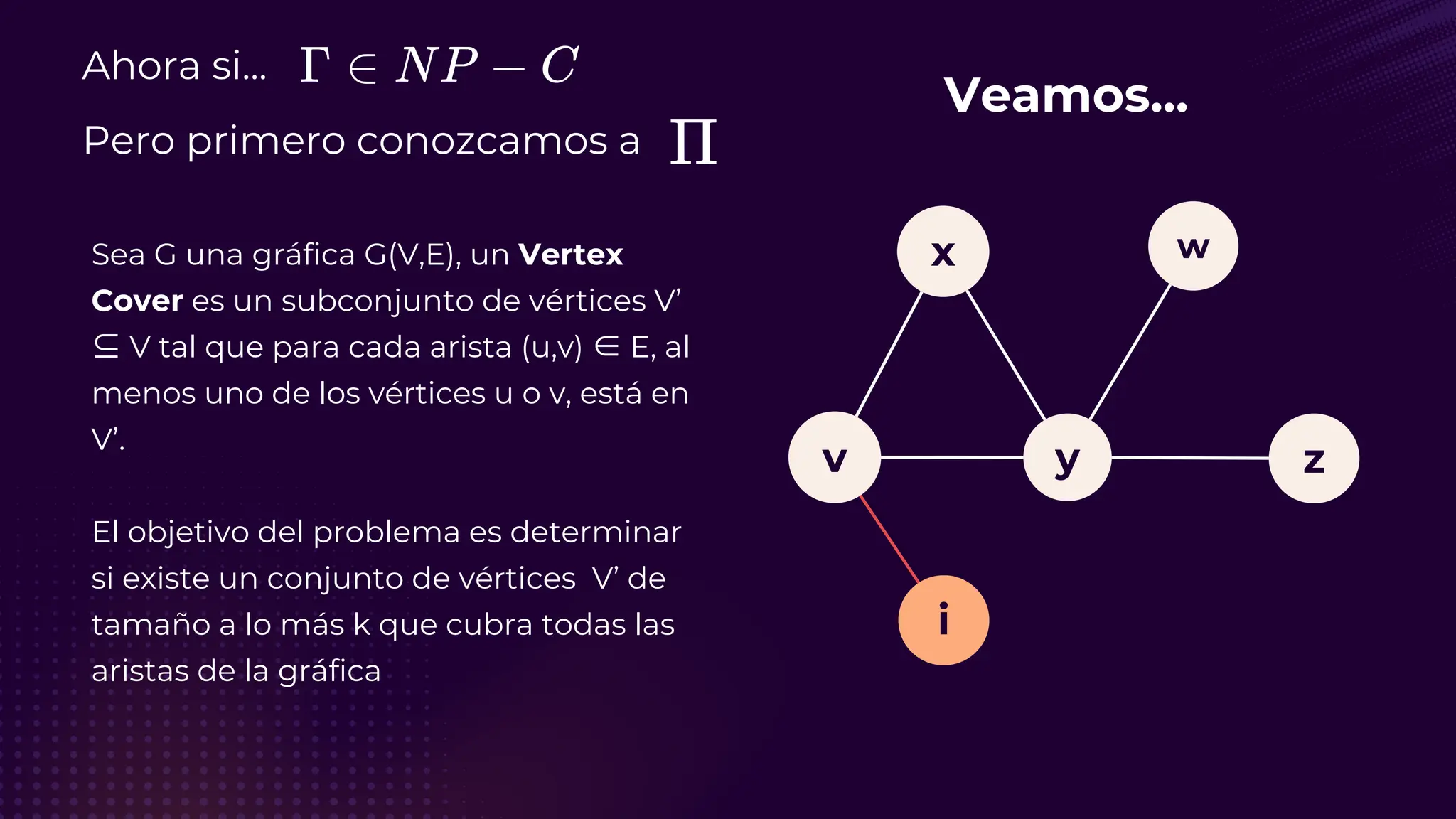
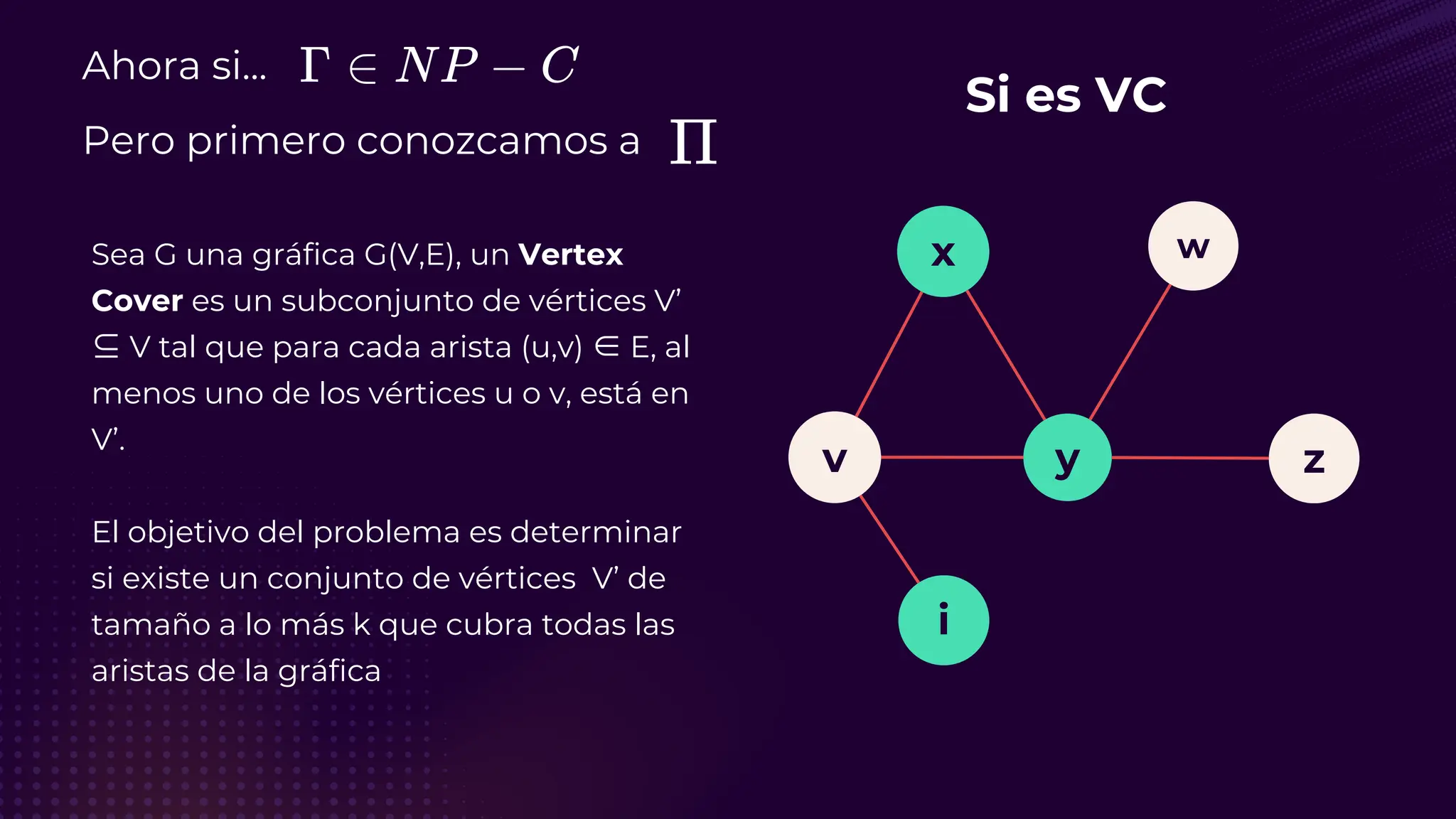
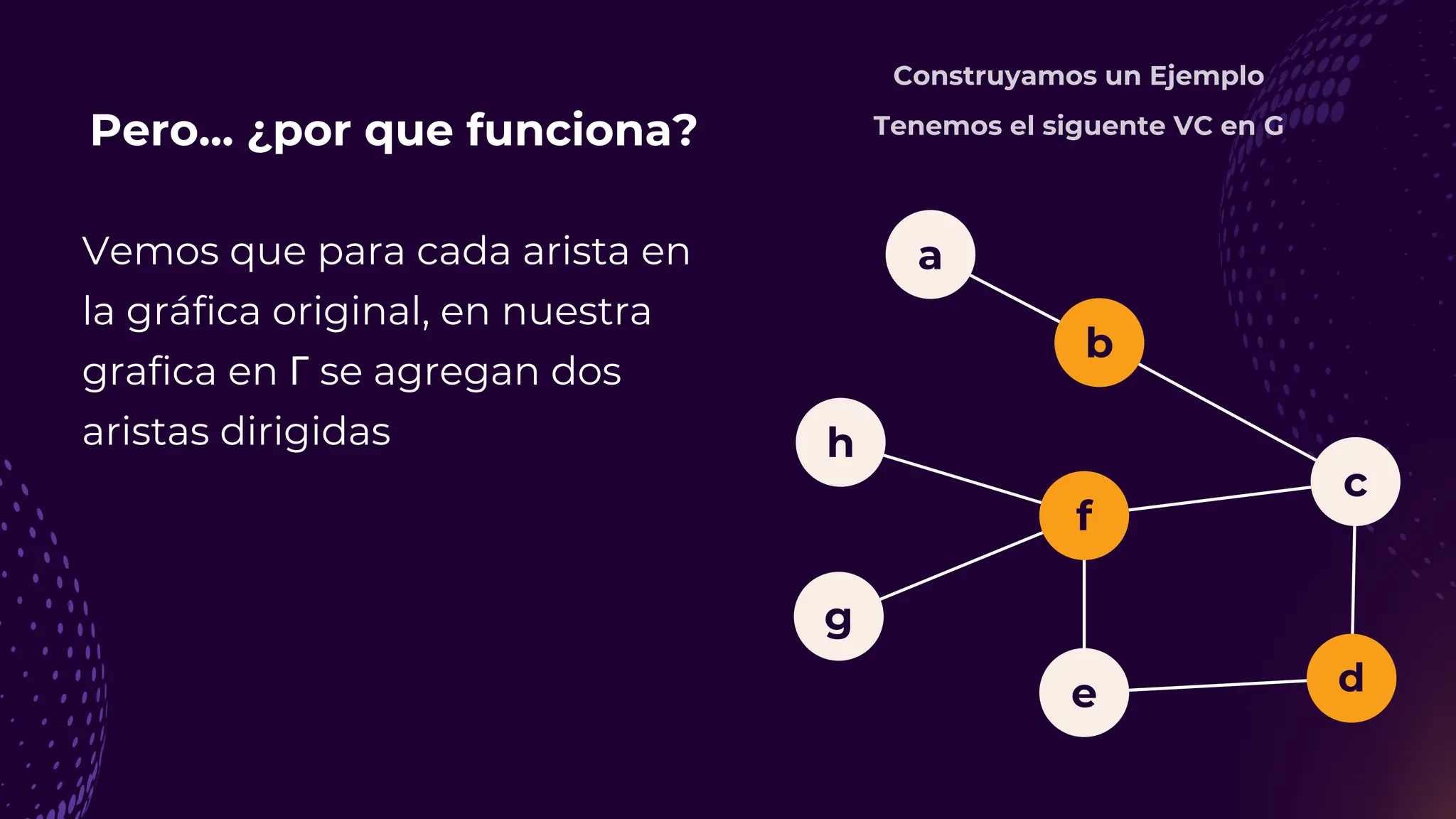
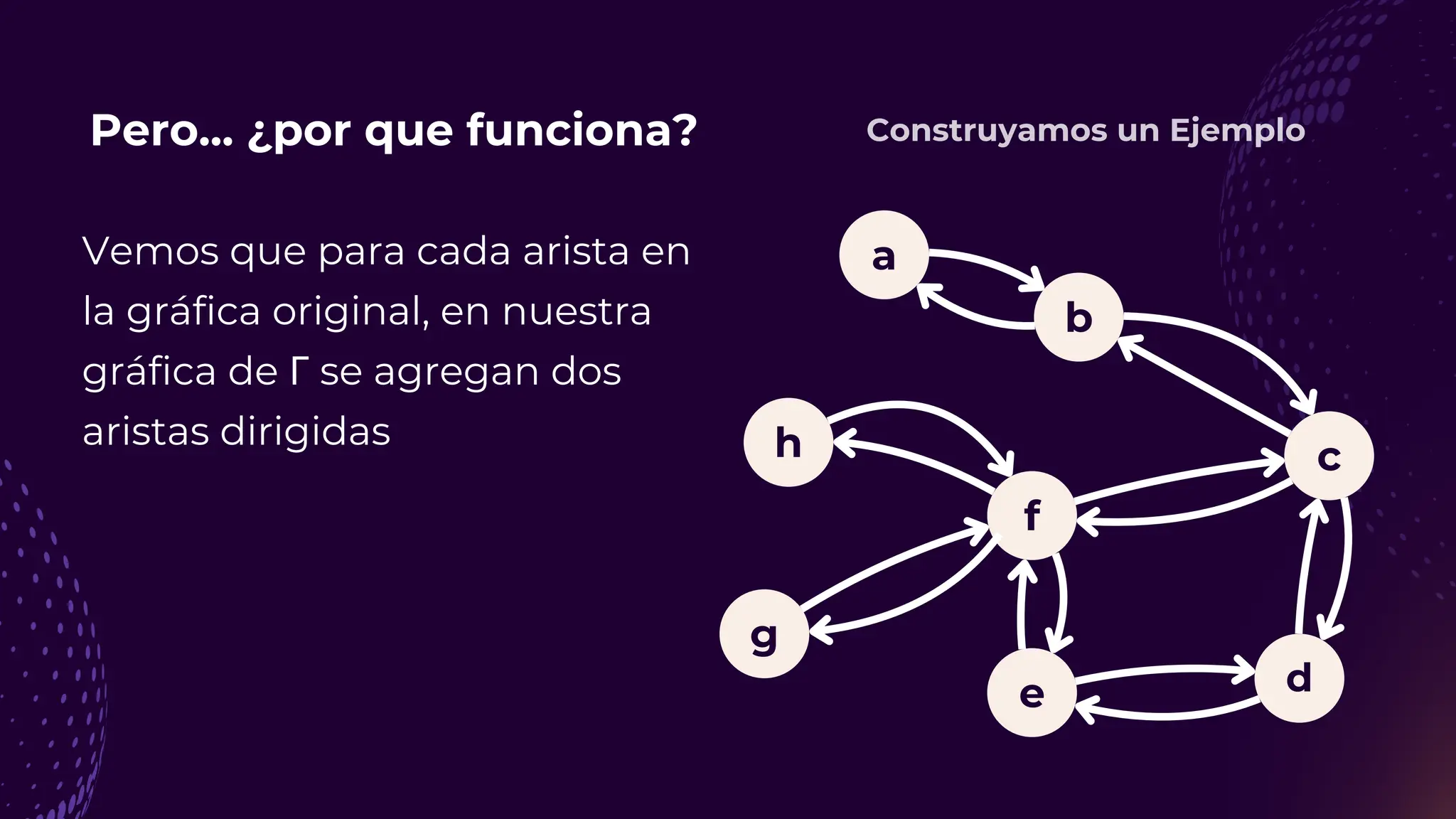
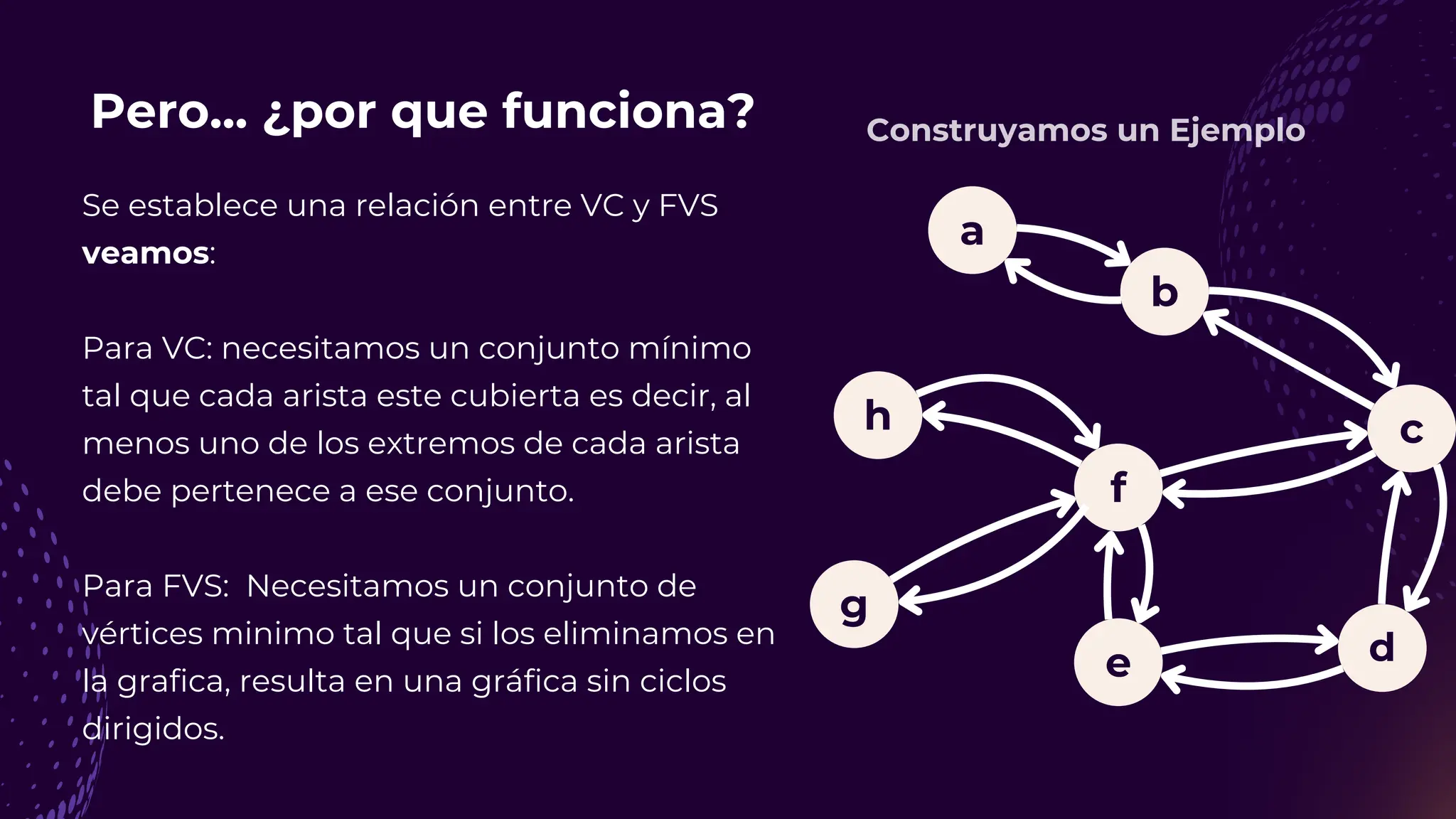
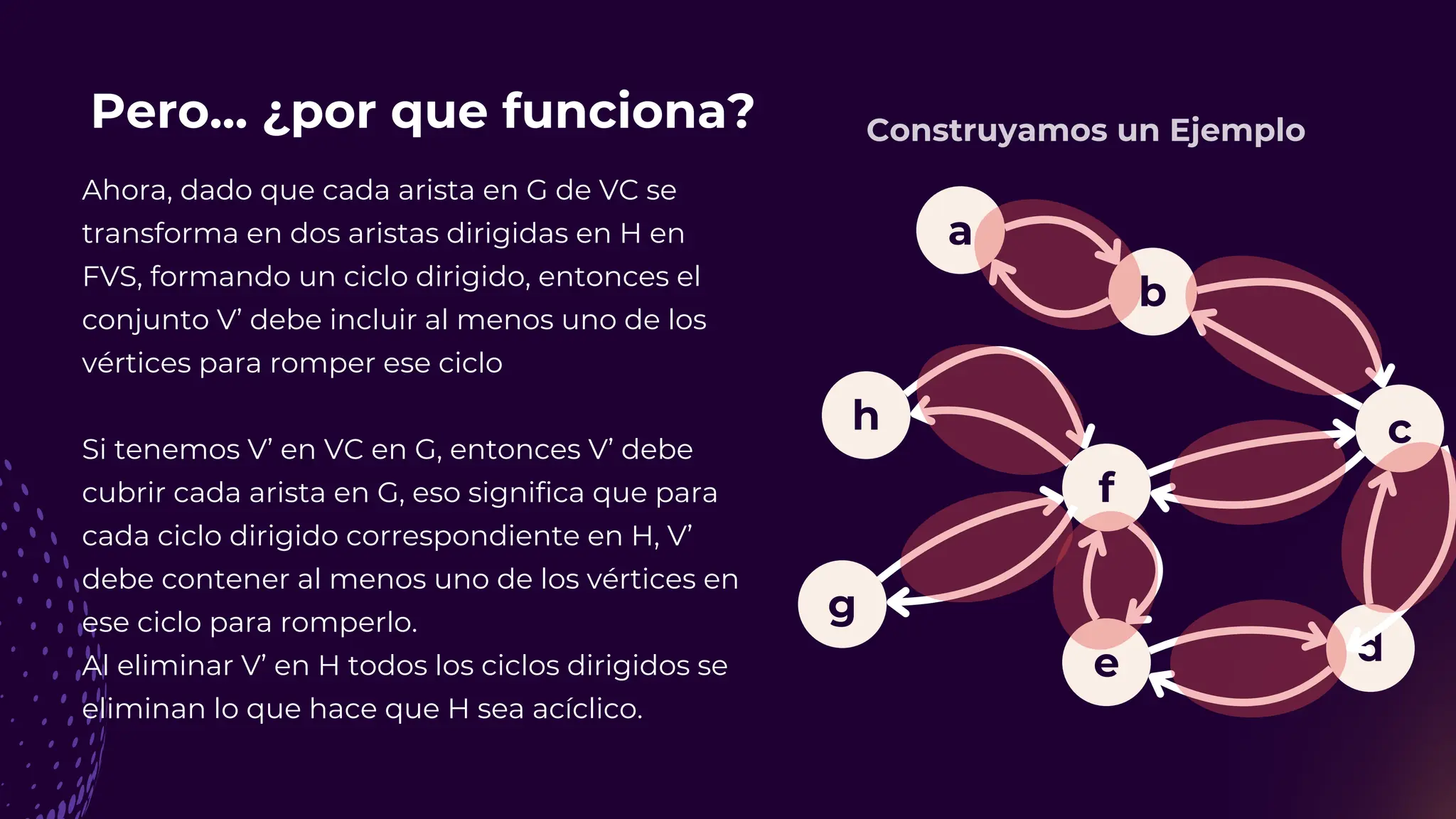
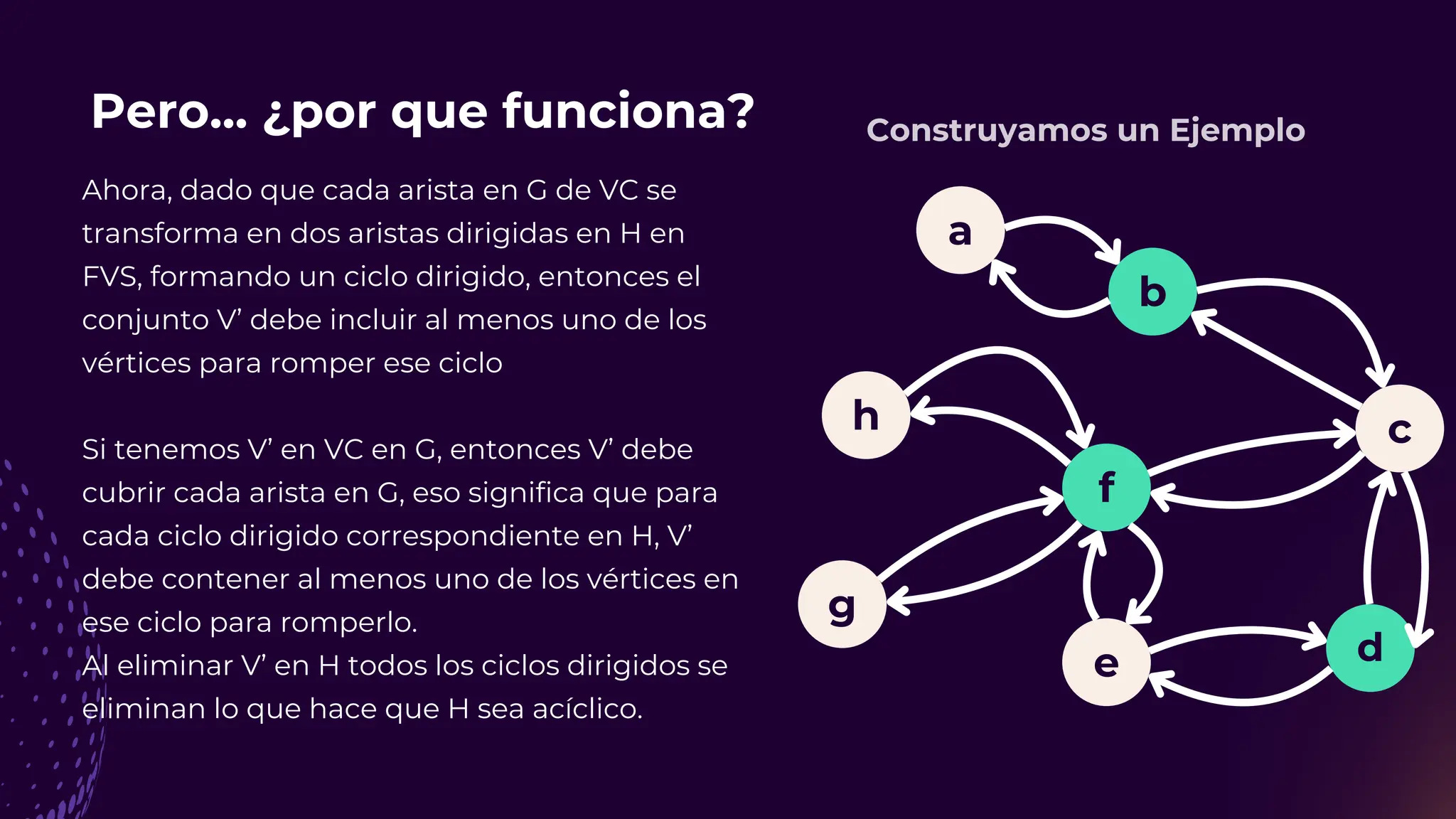
66. Referencias 🤓
Shimon Even. (1979). Graph algorithms (1.a ed.).
McCulloch, S. T. (2014, 10 junio). Exact Cover by 3-Sets | Discussions of NP-Complete
Problems. https://npcomplete.owu.edu/2014/06/10/exact-cover-by-3-sets/
Algorithms Live! (2017, 18 febrero). Episode 7 - Steiner Trees [Vídeo]. YouTube.
https://www.youtube.com/watch?v=BG4vAoV5kWw
☝🏼

67. Es cine
Fin (Halt)