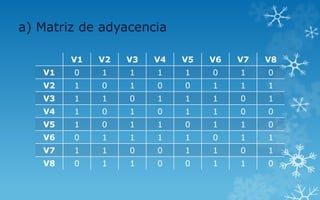
El documento contiene ejercicios propuestos para la asignatura de Estructuras Discretas II de la estudiante Ana G. García para la Universidad Fermín Toro. Se piden calcular la matriz de adyacencia y de incidencia de un grafo, determinar si es conexo, simple, regular o completo, encontrar una cadena y un ciclo en el grafo, construir un árbol generador y un subgrafo parcial, y demostrar si es euleriano u hamiltoniano.

1. Estructura
Discretas II
Ejercicios propuestos
Estudiante
Ana G. García Seekatz
20.927.478
REPÚBLICA BOLIVARIANA DE VENEZUELA
VICERRECTORADO ACADÉMICO
UNIVERSIDAD FERMÍN TORO FACULTAD
FACULTAD DE INGENIERÍA
Estructura
Discretas II
Ejercicios propuestos
Estudiante
Ana G. García Seekatz
20.927.478
REPÚBLICA BOLIVARIANA DE VENEZUELA
VICERRECTORADO ACADÉMICO
UNIVERSIDAD FERMÍN TORO FACULTAD
FACULTAD DE INGENIERÍA

2. Dado el siguiente grafo, encontrar:
a) Matriz de adyacencia
b) Matriz de incidencia
c) Es conexo?. Justifique su respuesta
d) Es simple?. Justifique su respuesta
e) Es regular?. Justifique su
respuesta
f) Es completo? Justifique su
respuesta
g) Una cadena simple no elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es euleriano aplicando el algoritmo de
Fleury
l) Demostrar si es hamiltoniano

3. V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 1 0 1 0
V2 1 0 1 0 0 1 1 1
V3 1 1 0 1 1 1 0 1
V4 1 0 1 0 1 1 0 0
V5 1 0 1 1 0 1 1 0
V6 0 1 1 1 1 0 1 1
V7 1 1 0 0 1 1 0 1
V8 0 1 1 0 0 1 1 0
a) Matriz de adyacencia

4. a
1
a
2
a
3
a
4
a
5
a
6
a
7
a
8
a
9
a
1
0
a
1
1
a
1
2
a
1
3
a
1
4
a
1
5
a
1
6
a
1
7
a
1
8
a
1
9
a
2
0
V
1
1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
V
2
1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
V
3
0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
V
4
0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
V
5
0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
V
6
0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
V
7
0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
V
8
0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
b) Matriz de incidencia

5. c) Es conexo?. Justifique su respuesta.
Se dice Conexo si para cualquier par de vértices de a y b en G existe al menos una
trayectoria (una secuencia de vértices adyacentes que no repita vértices) de a á b.
De acuerdo con la definición, si es conexo ya que, para todo par de vértices se
encuentran
conectados o tienen un camino que los una.
d) Es simple?. Justifique su respuesta.
Si es un grafo simple, debido a que se cumple que ningún vértice tiene lazo, además
cada vértice esta unido por una sola arista; pero todos los vértices poseen un grado
diferente, siendo no regular.
e) Es Regular? Justifique su respuesta.
¿Regular?: Es un grafo donde cada vértice tiene el mismo grado o valencia.
Grado de un vértice es: El número de aristas que inciden en el vértice.
No es un grafo regular, ya que hay vértices que tienen grados o valencias diferentes.
f) Es Completo? Justifique su respuesta.
Completo?: Es aquel grafo con N vértices, en las que existe únicamente una arista por
cada par de vértices. No hay aristas paralelas o sub. Grafos.
En conclusión podemos decir que NO es Completo, porque posee aristas paralelas y más
de
una arista por cada par de vértices, dando origen a los sub. Grafos.

6. G) Una cadena simple no elemental de
grado 6.
Una cadena simple es una secuencia finita alternada de vértices y aristas, sin repetir
aristas,
no elemental indica que puede repetirse los vértices. El grado nos indica la cantidad de
aristas que debe contener la cadena, en esta oportunidad son seis (6).
Ejemplo:
V3= GRADO 6
V6= GRADO 6
h) Un ciclo no simple de grado 5.
Ciclo simple es: Es el ciclo que a su vez es una cadena simple.
Ciclo no simple: Es un ciclo que no es una cadena simple.
No se puede demostrar, ya que todas las aristas son distintas del grafo. No hay cadenas
no simples de ningún grado.
I) Árbol generador aplicando el algoritmo
constructor.
1er paso: Seleccionar un vértice S1, hacer H1={S1}
2do paso: Seleccionamos una arista a1que tenga un extremo en H1y el otro extremo en
un vértice S2 ∉ H1. Hacer H1 ∪ {S2}

7. 3er paso: Seleccionamos una arista a2 que tenga un extremo en H2, y el otro extremo
en un vértice S3 ∉ H2. Hacer H2 ∪ {S3}
Seleccionamos el vértice v1 ⇒ H1={v1}
Seleccionamos la arista a4 ⇒ H2={v1,v4}
A15 ⇒ H3={v1,v4, v5}
A12 ⇒ H4={v1,v4, v5, v3}
A13 ⇒ H5={v1,v4, v5, v3, v6}
A8 ⇒ H6={v1,v4, v5, v3, v6, v2}
A10 ⇒ H7={v1,v4, v5, v3, v6, v2, v8}
A20 ⇒ H8={v1,v4, v5, v3, v6, v2, v8, v7}
v1
v4
a4
v1
v4
v5
v3
v6
v1
v4
v5
v3
v6
v2
v8

8. Por lo tanto se comprueba que en un árbol dos vértices cualesquiera están unidos
Por un único camino, se demuestra con al poseer árbol generador que es un grafo
conexo, y que G es un árbol entonces el número de aristas es igual al número de
vértices menos 1.
A = {a4, a15, a12, a3, a8, a10, a20}
V = {v1,v4, v5, v3, v6, v2, v8, v7}
Numero de vértices = 8 - 1 = 7
Numero de aristas = 7
j) Subgrafo Parcial.
Un subgrafo parcial se obtiene al conservar todos los nodos o vértices de G y se
suprimen algunas aristas.
Tenemos
v1
v4
v5
v3
v6
v2
v8
v7

9. v1
a2
v3
a3
v2
v4
a15
v5
a17
v6
a19
v7
a20
v8
k) Demostrar si es euleriano aplicando el
algoritmo de Fleury
Si el grafo es euleriano a partir de un vértice cualquiera de G se puede construir una
cadena
simple de manera que no se repitan las aristas y no se elijan aristas de corte a no ser que
no
se encuentre otra alternativa, al haber agotado las aristas decimos que tenemos un tour
euleriano. Luego de experimentar en repetidas ocasiones el recorrido del grafo sin repetir
aristas, no ha sido posible encontrar un camino euleriano donde no se repitan aristas, por
lo tanto no se cumple que el Grafo sea Euleriano.

10. I) Demostrar si es Hamiltoniano
Un grafo es hamiltoniano si contiene un ciclo hamiltoniano, en el cual se debe cumplir
que atraviese cada vértice del grafo exactamente una vez.
el ciclo C=[v1, a3, v2, a10, v8, a20, v7, a19, v6, a17, v5, a15, v4, a11,v3, a2, v1]
Notamos que Vo = Vk
v1 a3 v2
a10
v8
a20
v7
a19v6
a17
v5
a15
v4
a11 v3
a2

11. Dado el siguiente dígrafo
a) Encontrar matriz de conexión
b) Es simple?. Justifique su respuesta
c) Encontrar una cadena no simple no
elemental de grado 5
d) Encontrar un ciclo simple
e) Demostrar si es fuertemente conexo utilizando la
matriz de accesibilidad
f) Encontrar la distancia de v2 a los demás vértices
utilizando el algoritmo de Dijkstra
Ponderación de las aristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponder. 2 3 4 3 2 3 4 1 4 3 2 2 4 3

12. a1
a
2
a3
a
4
a5
a
6
a7 a8 a9
a1
0
a1
1
a1
2
a1
3
a1
4
V1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
V2 1 0 0 0 0 0 0 0 0 1 0 0 0 0
V3 0 1 0 0 1 0 0 0 0 0 0 0 0 0
V4 0 0 1 0 0 0 0 1 0 0 1 0 0 0
V5 0 0 0 0 0 1 1 0 0 0 0 0 0 1
V6 0 0 0 1 0 0 0 0 0 0 0 1 1 0
a) Encontrar matriz de conexión

13. b) Es simple?. Justifique su respuesta
Se cumple que el Dígrafo es simple, ya que no tiene lazos y no existen arcos paralelos
que partan de un mismo vértice a otro.
c) Encontrar una cadena no simple no elemental de grado 5
En las cadenas no simples se pueden repetir los arcos durante el recorrido y que sea no
elemental, también nos permite repetir vértices. El grado 5 nos indica el número de arcos que
tendrá nuestra cadena.
T = [v4, 9, v1, 5, v3, 8, v4, 9, v1, 6, v5]
d)Encontrar un ciclo simple
El ciclo simple inicia y termina con el mismo vértice y en ella no se pueden repetir arcos.
C = [v6, 14, v5, 11, v4, 9, v1, 1, v2, 4, v6 ]
e) Demostrar si es fuertemente conexo utilizando la matriz de
accesibilidad
Para comprobar que un grafo es conexo podemos realizar los siguientes pasos:
1) Hallar la matriz de adyacencia y se eleva a la enésima potencia.
2) Se calcula la suma de las potencias de A hasta An.
3) Si todos sus elementos son distintos de cero, el grafo es conexo

14. V
1
V
2
V
3
V
4
V
5
V
6
V
1
0 1 1 0 1 0
V
2
0 0 1 1 0 1
V
3
0 0 0 1 1 0
V
4
1 0 0 0 0 1
V
5
0 1 0 1 0 1
V
6
0 0 0 0 1 0
Matriz de adyacencia
Ma(D)=
V
1
V
2
V
3
V
4
V
5
V
6
V
1
0 0 1 1 1 1
V
2
1 0 0 1 1 1
V
3
1 1 0 1 0 1
V
4
0 1 1 0 1 0
V
5
1 0 1 1 1 1
V
6
0 1 0 1 0 1
Elevamos la matriz al cuadrado para
encontrar los caminos de tamaño dos
(02)
M
(D)=
2

15. V
1
V
2
V
3
V
4
V
5
V
6
V
1
1 1 1 1 1 1
V
2
1 1 1 1 1 1
V
3
1 1 1 0 1 1
V
4
0 1 1 1 1 1
V
5
0 1 1 1 1 1
V
6
1 0 1 1 0 1
V
1
V
2
V
3
V
4
V
5
V
6
V
1
1 1 1 1 1 1
V
2
1 0 1 1 1 1
V
3
0 1 1 1 1 1
V
4
1 1 0 1 1 1
V
5
1 1 1 1 1 1
V
6
1 1 1 1 0 1
Elevamos la matriz a cuatro para
encontrar los caminos de tamaño cuatro
(04)
M
(D)=
4
Elevamos la matriz al cubo para encontrar
los caminos de tamaño tres (03)
M
(D)=
3

16. V
1
V
2
V
3
V
4
V
5
V
6
V
1
1 1 1 1 1 1
V
2
1 1 1 1 1 1
V
3
1 1 1 1 1 1
V
4
1 1 1 1 1 1
V
5
1 1 1 1 1 1
V
6
1 1 1 1 0 1
V
1
V
2
V
3
V
4
V
5
V
6
V
1
1 1 1 1 1 1
V
2
1 0 1 1 1 1
V
3
0 1 1 1 1 1
V
4
1 1 0 1 1 1
V
5
1 1 1 1 1 1
V
6
1 1 1 1 0 1
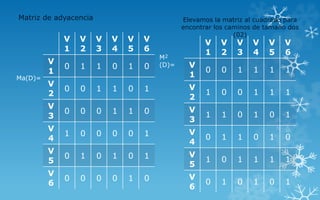
Ahora calculamos la Matriz de Accesibilidad
Acc(D) = bin [I6 + M + M + M + M + M
]
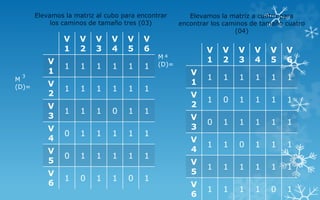
Elevamos la matriz a la cinco para
encontrar los caminos de tamaño cinco
(05)
M
(D)=
5
2 3 4 5
Acc(D)= bin

17. V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 1 1
Luego transformamos la matriz de la manera siguiente:
a) Componente que sea igual a cero (0), permanece como cero (0)
b) Componente diferente de cero (0), convertirla a 1.
Acc(D)= bin
Como la matriz Acc(D) no tiene componentes nula se dice entonces según el colorario 1.2
que el dígrafo es fuertemente conexo.

18. F) Encontrar la distancia V2 a los de más vértices
utilizando el algoritmo de DIJKSTRA
Pasos:
1) Ubicar el vértice de inicio.
2) Luego ubicar los vértices mas cercanos al V2 para estudiarlo, lo que esté directamente a él.
3) Agregar etiquetas a cada vértice estudiado, la misma se realiza así:
4) Luego colocar la ponderación de la arista + la ponderación de la etiqueta anterior que esta
directamente al vértice estudiado.
5) Colocara al lado de la etiqueta el numero de iteración que se esta realizando.
6) Luego se estudian las distancias y se escoge la menor, si hay 2 igual se escoge
cualquiera de la dos.
[3,1]Símbolo de la iteración
o estudio de distancia
Ponderación de la arista
+ lo que precede
Vértice estudiado
(1,1)# de la iteración

19. d v2 a v1: 2
d v2 a v3: 3
d v2 a v5: 3
d v2 a v4: 4
d v2 a v6: 3
[2,2](1)
[3,2](1)
[3,2](1)
[0,](0)
Ponderación de las aristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponder 2 3 4 3 2 3 4 1 4 3 2 2 4
3