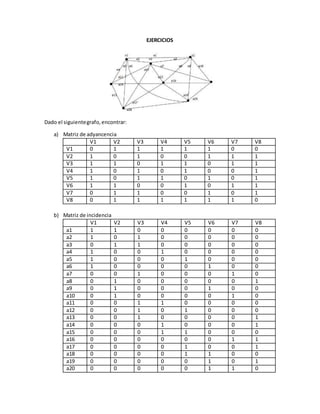
El documento presenta una serie de ejercicios sobre grafos, incluyendo la construcción de matrices de adyacencia e incidencia, así como análisis sobre la conexión, simplicidad y completitud del grafo correspondiente. Se aborda también la verificación de propiedades como ser euleriano y hamiltoniano, además de aplicar el algoritmo de Dijkstra para calcular distancias entre vértices. A través de ejemplos y justificaciones, se exploran diversas características de estructuras de grafos.

1. UNIVERSIDAD "FERMÍN TORO"
SISTEMAS INTERACTIVOS DE EDUCACIÓN A DISTANCIA (SAIA)
CABUDARE.
APELLIDOY NOMBRE: HidalgoMedwini
SECCIÓN SAIA:SaiaA
PROFESOR:FreitezEdecio
FECHA: 17/12/2018

2. EJERCICIOS
Dado el siguientegrafo,encontrar:
a) Matriz de adyancencia
V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 1 1 0 0
V2 1 0 1 0 0 1 1 1
V3 1 1 0 1 1 0 1 1
V4 1 0 1 0 1 0 0 1
V5 1 0 1 1 0 1 0 1
V6 1 1 0 0 1 0 1 1
V7 0 1 1 0 0 1 0 1
V8 0 1 1 1 1 1 1 0
b) Matriz de incidencia
V1 V2 V3 V4 V5 V6 V7 V8
a1 1 1 0 0 0 0 0 0
a2 1 0 1 0 0 0 0 0
a3 0 1 1 0 0 0 0 0
a4 1 0 0 1 0 0 0 0
a5 1 0 0 0 1 0 0 0
a6 1 0 0 0 0 1 0 0
a7 0 0 1 0 0 0 1 0
a8 0 1 0 0 0 0 0 1
a9 0 1 0 0 0 1 0 0
a10 0 1 0 0 0 0 1 0
a11 0 0 1 1 0 0 0 0
a12 0 0 1 0 1 0 0 0
a13 0 0 1 0 0 0 0 1
a14 0 0 0 1 0 0 0 1
a15 0 0 0 1 1 0 0 0
a16 0 0 0 0 0 0 1 1
a17 0 0 0 0 1 0 0 1
a18 0 0 0 0 1 1 0 0
a19 0 0 0 0 0 1 0 1
a20 0 0 0 0 0 1 1 0

3. c) Es conexo?.Justifiquesurespuesta
Sí, esconexo,yaque segúnla definición,estatiene uncaminosimpleque vade unvértice
a otro.
d) Es simple?.Justifique surespuesta
Sí es simple,debidoaque lasaristasno se repitenenningúnlado.
e) Es regular?.Justifique surespuesta
No esregularya que el vértice notiene el mismovalorogrado.
f) Es completo?Justifiquesurespuesta
No loes.Ya que pordefinicióncadavértice debeestarconectadoportodaslas aristasy el
ejemplonoloestá.
g) Una cadena simple noelementalde grado6
C= v1 a1 v2 a10 v7 a16 v8 a14 v4 a11 v3 a3 v2.
h) Un ciclo nosimple de grado5
C= v8 a17 v5 a15 v4 a14 v8 a17 v5 a18 v6.
i) Arbol generadoraplicandoel algoritmoconstructor.
1. H={v1}
2. H={v1,v4}
3. H={v1,v4,v3}
4. H={v1,v4,v3,v5}
5. H={v1,v4,v3,v5,v8}
6. H={v1,v4,v3,v5,v8,v6}
7. H={v1,v4,v3,v5,v8,v6,v2}
v1
v2
v4 v3
v8
v5 v6
j) Subgrafoparcial
v1
v2
v3
v4
v8 v7
v5 v6
k) Demostrarsi es eulerianoaplicandoel algoritmode Fleury

4. 1. Seleccionamos=v4,a15, v5
2. Seleccionamos=v5,a18, v6
3. Seleccionamos=v6,a19, v8
4. Seleccionamos=v8,a17, v5
5. Seleccionamos=v5,a12, v3
6. Seleccionamos=v3,a11, v4
7. Seleccionamos=v4,a14, v8
8. Seleccionamos=v8,a13, v3
9. Seleccionamos=v3,a3, v2
10. Seleccionamos=v2, a8, v8
11. Seleccionamos=v8,a16, v7

5. 12. Seleccionamos=v7,a10, v2
13. Seleccionamos=v2,a9, v6
14. Seleccionamos=v6,a20, v7
15. Seleccionamos=v7,a7, v3
16. Seleccionamos=v3,a2, v1
17. Seleccionamos=v1,a6, v6
No existe uncicloeuleriano eneste ejemplo.
l) Demostrarsi es hamiltoniano
Sí lo esdebidoa= {v1, a2, v3, a3, v2, a9, v6, a19, v8, a17, v5, a15, v4, a4}

6. Dado el siguientedígrafo
a) Encontrar matrizde conexión
V1 V2 V3 V4 V5 V6
A1 0 1 0 0 0 0
A2 0 0 1 0 0 0
A3 0 0 0 1 0 0
A4 0 0 0 0 0 1
A5 0 0 1 0 0 0
A6 0 0 0 0 1 0
A7 0 0 0 0 1 0
A8 0 0 0 1 0 0
A9 1 0 0 0 0 0
A10 0 1 0 0 0 0
A11 0 0 0 1 0 0
A12 0 0 0 0 0 1
A13 0 0 0 0 0 1
A14 0 0 0 0 1 0
b) Es simple?.Justifique surespuesta
Sí, ya que no tiene lazosni arcosentre susvérticesque permitanrepetiralguna.
c) Encontrar una cadenano simple noelementalde grado5
C= {V1, A6, V5,A11, V4, A12, V6, A14, V5}
V1
A6 V4
A12
A11
V5 v6
A14
d) Encontrar un ciclosimple
C= {V1, A1, V2,A3, V4, A9, V1}
V1 A1 V2
A3
A9 V4

7. e) Demostrarsi es fuertemente conexoutilizandolamatrizde accesibilidad
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
V1 V2 V3 V4 V5 V6
V1 0 0 1 1 1 1
V2 1 0 0 1 1 1
V3 1 1 0 1 0 1
V4 0 1 1 0 1 0
V5 1 0 1 1 1 1
V6 0 1 0 1 0 1
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 0 1 1
V4 0 1 1 1 1 1
V5 0 1 1 1 1 1
V6 1 0 1 1 0 1
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 0 1 1 1 1
V3 0 1 1 1 1 1
V4 1 1 0 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1

8. V1 V2 V3 V4 V5 V6
V1 3 4 5 4 5 4
V2 4 2 5 5 5 5
V3 3 4 3 4 4 4
V4 4 4 3 5 4 4
V5 3 4 4 5 4 5
V6 3 3 3 4 1 4
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 1 1
f) Encontrar la distanciade v2 a losdemásvérticesutilizandoel algoritmode Dijkstra
Ponderaciónde lasaristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponder.2 3 4 3 2 3 4 1 4 3 2 2 4 3
V2 A V3=3
V2 A V4= 4
V2 A V6= 3
V2 A V5= 6
V2 A V1= 8
[8,4]3
[3,2]1
[0,1]0
[6,6]1
[4,3]2
[3,2]1