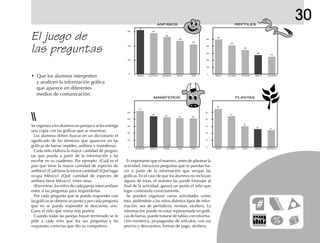
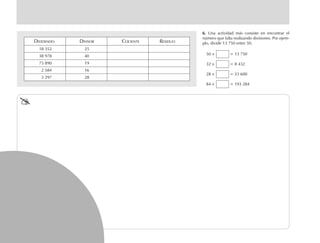
Este documento presenta datos estadísticos sobre el número de hablantes de diferentes lenguas indígenas en el estado de Chiapas, México. Los alumnos deben completar la tabla con los números de hablantes, ordenar las lenguas de mayor a menor, calcular el total de hablantes de lenguas indígenas y calcular cuántas personas no hablan ninguna lengua indígena basándose en la población total del estado. El objetivo es que interpreten e interactúen con información numérica presentada en una tabla.