1. La guía explica cómo utilizar de forma efectiva los materiales para mejorar la enseñanza de las matemáticas. 2. Está dividida en tres partes: estructura y aplicación de la guía, desarrollo de clases por unidad, y columnas que explican conceptos clave. 3. Cada unidad sigue una estructura definida y proporciona objetivos, actividades, y sugerencias para el maestro.

1. Guía para Maestros y Maestras
MatemáticaGuíaparaMaestrosyMaestras
Matemática
Agencia de Cooperación
Internacional del Japón
Instituto Nacional de
Formación
y
Capacitación del
Magisterio PROYECTO REGIONAL
Me gusta¡
!Matemática JAPÓNAsistencia oficial para el Desarrollo
Grado2do
Grado
2do

2. PRESENTACIÓN
El Ministerio de Educación, comprometido con elevar el nivel de la Calidad de la
educación dominicana, pone a disposición de los y las docentes del Primer Ciclo del Nivel
Básico la guía “Matemática, Guía para Maestros y Maestras” y su correspondiente “Libro
de Estudiantes” para el estudiante, como una valiosa herramienta para mejorar la enseñanza
y la práctica de esta área en el aula.
Esta Guía fue elaborada en el marco del proyecto “Mejoramiento de la Calidad de la
Enseñanza de la Matemática, 2005-2010”, realizado en la República Dominicana, con el
apoyo de la Agencia de Cooperación Internacional del Japón (JICA). El documento constituye
una adaptación a nuestro contexto de los materiales “guía para el docente” y “cuaderno de
trabajo del estudiante”, elaborados en Honduras con la asesoría de expertos japoneses.
Las unidades de esta guía fueron adecuadas por un equipo técnico que recibió capacitación
y asesoría técnica para tal fin, durante el desarrollo del Proyecto Regional “Me Gusta
Matemática”, en Honduras y en la Universidad de Tsukuba, en Japón.
En el diseño, la guía está organizada por unidades, las cuales están orientadas a partir de los
contenidos curriculares y los componentes psicopedagógicos del Área de Matemática que se
desarrollan en el Primer Ciclo del Nivel Básico.
En el proceso de adecuación participaron en forma activa la Dirección General de Currículo,
la Dirección General de Nivel Básico y el Instituto Nacional de Formación y Capacitación del
Magisterio (INAFOCAM) que tuvo la función de coordinación.
Para un óptimo aprovechamiento de este recurso didáctico, se recomienda utilizar el
correspondiente cuaderno de trabajo dirigido a los niños y las niñas de este ciclo, de igual
modo se espera que los Maestros y Maestras hagan un uso eficiente de estos materiales,
para mejorar el aprendizaje de la Matemática en la escuela dominicana.
Josefina Pimentel, M.A.
Ministra de Educación

3. INTRODUCCIÓN
El libro “Matemática, Guía para Maestros y Maestras” (GM), está compuesta por tres partes.
La primera, se refiere a la estructura y aplicación de la Guía. La segunda, describe el desarrollo
de las clases de cada unidad, con sus páginas modelos para recortar y un apéndice que ayuda
a la diversidad en el aprendizaje de los los alumnos y las alumnas. La tercera, se dedica al es-
pacio denominado “Columnas”, donde se explican algunas ideas para reforzar el tema que se
desarrolla en una determinada clase o lección.
En la primera parte, “estructura y aplicación de la guía”, se señalan con detalles los objetivos,
estructura, instructivo, ejemplo del desarrollo de una clase y el programa anual. Como se pue-
de apreciar, este apartado consta de cinco aspectos que son fundamentales dominar antes de
trabajar con las unidades. La forma en que están distribuidas las lecciones, el sentido de cada
apartado y de cada símbolo o palabra utilizados en el desarrollo de las unidades, son explicadas
en esta sección, donde se incluyen modelos que permiten la reflexión de la práctica, un camino
excelente para la autoformación del profesorado.
En la segunda parte, se desglosa el “desarrollo de la clase de cada unidad”, tomando en
cuenta los requisitos del grado en un año escolar y los requerimientos curriculares de nuestro
Sistema Educativo Nacional. Se presentan 11 unidades desarrolladas en lecciones. Cada una
de ellas contiene los objetivos, las expectativas de logro, las estrategias para el aprendizaje, las
actividades y los recursos educativos a utilizar para orientar la clase de cada día.
Se indican las “páginas para recortar” con plantillas que pueden ser usadas durante el desarro-
llo de la clase, por lo cual, resulta interesante recortarlas o fotocopiarlas para complementar la
acción didáctica.
Otra sección es “apéndice” allí se encuentran algunos ejercicios complementarios como ilus-
tración para la elaboración de otros juegos o entretenimientos matemáticos. Son útiles para
las situaciones en que un alumno o una alumna logra el objetivo de la clase más rápido que
la mayoría. Crear nuevos desafíos puede ayudarles a mantener el interés por la clase, mien-
tras el maestro o la maestra atiende otros alumnos y otras alumnas que aún no han logrado la
comprensión del tema.
En la tercera parte, “Columnas” de la Guía para Maestros y Maestras, explican detalles del
contenido de algunas unidades. Conviene detenerse en la lectura de este apartado, para poseer
más claridad del por qué de algunas ideas que se presentan durante el desarrollo de algunas
unidades o lecciones.

4. Guía para maestros/as - Matemática 20
grado I
Estructura y aplicación de la Guía
Desarrollo de clases de cada unidad
Números hasta 999
Números ordinales
Suma
Resta
Suma y resta combinada
Figuras geométricas
Multiplicación
Longitud
Estadística
Tiempo
Moneda nacional
2
24
28
50
70
78
86
124
134
140
150
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
Ejemplos de las páginas para recortar del Libro de Estudiantes
Nos divertimos
Apéndice
156
170
172
1.
2.
3.
4.
5.
Objetivo de la Guía
Estructura de la Guía
Instructivo para el uso de la Guía y del Libro de Estudiantes
Ejemplo del desarrollo de una clase
Programación anual
II
II
III
VII
XIV
Columnas
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
Unidad
1:
2:
3:
4:
6:
7:
8:
9:
10:
Los materiales didácticos
Los números ordinales del 21O
hasta el 100O
Tipos de suma
Tipos de la resta en el cálculo vertical
Uso de la regla para trazar líneas
El sentido de los factores en la multiplicación
La forma de medir con la regla
Forma de contar los correctamente la
cantidad de los elementos dibujados
Elaboración del reloj
5
25
31
52
79
90
125
135
141

5. Guía para maestros/as - Matemática 20
gradoII
Unidad 3 - Suma32
SumemosLección 1:
(1/3)
• Realizar los cálculos del tipo D0 + D0 en forma horizontal.
(M) azulejos
(N) azulejos
Objetivo:
Materiales:
5 Desarrollo de
clases
1. Comentar la situación del
problema. [A]
* Orientar para que piensen con
cuál operación se puede en-
contrar el resultado.
2. Escribir el planteamiento
de la operación. [A1]
M: ¿Cómo será el planteamiento
de la operación? Escríbanlo
en sus cuadernos.
* No es necesario resolver en
este momento.
3. Encontrar la manera de cal-
cular. [A2]
* Indicar que utilicen los azule-
jos para resolver.
M: ¿Cómo hicieron?
RP: Representé con los azulejos
dos grupos de 10 que es la
cantidad de flores que tenía
María y otro grupo de 10 que
son las flores que su mamá
le regaló, entonces sumé 2
grupos más 1 grupo de 10 es
igual a 30.
Que se den cuenta que con-
virtiendo a las decenas se
puede encontrar la respuesta
fácilmente.
4. Confirmar la manera de cal-
cular “20 + 10”.
* Indicar que observen el LE y
analizar el proceso.
M: ¿Por qué el resultado es trein-
ta?
* Si surge en los niños y las niñas
la idea de sumar sólo los núme-
ros de las decenas y agregar
0 para encontrar el resultado,
hay que felicitarlos y se puede
concluir de esta forma.
5. Resolver el ejercicio 1 .
Para afianzar el contenido del problema principal se
puede realizar otros ejemplos del mismo tipo antes de
resolver los ejercicios del LE.
Lección 1: Sumemos
Unidad 3
A María tiene 20 flores y su mamá le regala 10 flores más.
¿Cuántas flores tiene María ahora?
22 veintidós
Suma
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
20 + 10
Planteamiento de la operación: 20 + 10 = ___
Respuesta: flores
1 Calcule las siguientes sumas.
(1) 10 + 20 = ___ (2) 30 + 10 = ___ (3) 50 + 40 = ___
(4) 20 + 50 = ___ (5) 30 + 40 = ___ (6) 20 + 60 = ___
(7) 40 + 40 = ___ (8) 70 + 10 = ___ (9) 20 + 20 = ___
(10) 80 + 10 = ___ (11) 60 + 30 = ___ (12) 30 + 30 = ___
D U
2 0
D U
1 0
D U
3 0+ =
+
tiene 20 flores le regala 10 flores más
María Mamá
30
30
30 40 90
70 70 80
80 80 40
90 90 60
(1/3)
1. Objetivo de la Guía
Esta guía explica la programación anual y el desarrollo de las clases basados en el contenido Cu-
rricular del Nivel Básico (CNB). Si el maestro o la maestra aprovecha esta Guía, le ayudará a desa-
rrollar sus clases de forma efectiva y eficiente para el mejoramiento del aprendizaje de los niños y
las niñas.
2. Estructura de la Guía
Estructura global: Está formada por las siguientes partes “Estructura y aplicación de la Guía”,
que explica cómo se utiliza la Guía; ”Desarrollo de clases de cada unidad”, que representa un
ejemplo del plan de clase para desarrollar cada contenido usando el LE.
Estructura de la unidad: En cada unidad se desarrollan, paso a paso, los contenidos conceptua-
les y actitudinales tomados del CNB. Se incluyen pequeños artículos que explican de una manera
comprensible las informaciones suplementarias. La estructura que contiene los propósitos y objeti-
vos de cada unidad se explica detalladamente en el “Instructivo”.
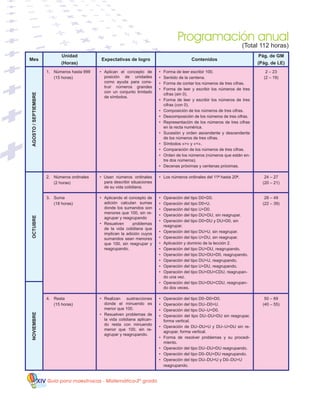
Número de
la lección
Actividades
de los niños y
las niñas en
cada etapa
Reacciones
previsibles
de los niños
y las niñas
Pensamiento o
actitud espera-
da de los niños
y las niñas
Preguntas,
comentarios
e indica-
ciones del
maestro o la
maestra
Puntos y su-
gerencias de
la enseñanza
y actividades
del maestro o
la maestra
Título
de la lección
Hora actual de
la clase / total
de horas
Objetivo de
cada clase
Materiales que
se utilizan en
cada clase
Pauta de
respuestas y
sugerencias
Página del LE
Informaciones
suplementarias
o ejercicios su-
plementarios
EstructurayaplicacióndelaGuía

6. Guía para maestros/as - Matemática 20
grado III
Esta Guía para Maestros y Maestras (GM)
fue diseñada con el propósito de orientar
el proceso para enseñar los contenidos
de matemática indicados en el Currículo
Nacional Básico (CNB). Su correcto uso
permitirá utilizar eficientemente el Libro
de Estudiantes (LE), que es un material
de apoyo para su aprendizaje.
Aunque se indica la manera de usar el
LE, y otros materiales didácticos, no ne-
cesariamante se describe la forma más
preferible para desarrollar la clase, porque
se ha intentado que los docentes puedan
dar la clase sin dedicar mucho tiempo a
los preparativos. Para elaborar un mejor
plan de estudio basado en la metodología
desarrollada en esta GM, consúltese a
«Ejemplo del desarrollo de una clase».
La GM se divide en dos grandes seccio-
nes: Programación anual y Desarrollo de
las clases de cada unidad.
Programación Anual
Es la lista de los contenidos del grado,
indicados en el CNB. En esta guía se pre-
sentan solamente las horas de las clases
fundamentales o mínimas, por lo que el
maestro o la maestra deberá agregar las
horas necesarias para fovorecer el rendi-
miento y la práctica de los niños y las niñas,
incluyendo las horas para las evaluaciones
a fin de cumplir con las jornadas estableci-
das por el Ministerio de Educación.
Si los niños y las niñas no manejan bien
los contenidos de cada grado, tendrán pro-
blemas con el aprendizaje en los grados
posteriores. Por ejemplo: el cálculo vertical
de la división, que es un contenido de 3er
grado, no se puede calcular si no se tienen
memorizadas las tablas de multiplicar (2do
grado) y la habilidad de la sustracción.
Desarrollo de las clases de cada unidad
Esta sección está dividida en cinco sub-
secciones: Espectativas de logro, Relación
y desarrollo, Plan de estudio, Puntos de
lección y Desarrollo de clase.
1 Expectativas de logro
Es el objetivo o propósito de cada unidad.
En esta guía las espectativas de logro es-
tán escritas en indicativo, sin embargo, los
objetivos de cada lección están redactados
en infinitivo.
2 Relación y desarrollo
Se enumeran los contenidos de la unidad
y su relación con otras unidades (ya sean
de este grado, anteriores o posteriores).
Las letras de color negro es el título que
se le ha dado a la unidad. Se usa el
cuadro de mayor densidad de color para
identificar la unidad actual de estudio. Los
y las docentes deben diagnosticar si los
niños y las niñas pueden manejar bien los
contenidos relacionados de los grados an-
teriores (véase la parte de «Recordemos»
en el LE). Si no, dependiendo del nivel de
insuficiencia en el manejo, se puede hacer
lo siguiente:
(a) Si la mayoría de los niños y las niñas
carecen de comprensión, de tal modo que
no se puede enseñar el contenido del gra-
do, se les da un repaso de dos o tres horas
clase. Para el mejor manejo del contenido,
es mejor darles tareas al mismo tiempo que
la enseñanza del contenido del grado.
(b) Si la mayoría entiende bien, se les
puede dar una orientación individual a los
demás niños y niñas.
Los contenidos actitudinales que se orien-
tan en el CNB para la adquisición y el
desarrollo de competencias relacionadas
con el quehacer matemático, en esta guía
no aparecen explícitamente definidos, sin
embargo se aplican en las actividades del
desarrollo de cada clase de forma que los
niños y las niñas incrementen la actitud de
3. Instructivo para el uso de la Guía para Maestros y
Maestras, y del Libro de EstudiantesInstructivo

7. Guía para maestros/as - Matemática 20
gradoIV
curiosidad, resolución de problemas, ejer-
citación del hábito del trabajo individual
y grupal, respeto a las opiniones ajenas,
placer por los desafíos intelectuales, entre
otros, de modo que la acción educativa in-
tegra los contenidos conceptuales, proce-
dimentales y actitudinales indispensables
para la formación de los educandos y que
a la vez, estos aprendizajes significativos
puedan ser utilizados en la vida cotidiana.
3 Plan de estudio
Se indica la distribución de las horas y el
contenido. Como el tiempo total de la clase
de matemáticas es limitado, no se reco-
mienda utilizar todo el tiempo disponible
para cubrir sólo unas cuantas unidades.
4 Puntos de leccion
Como cada unidad está dividida en leccio-
nes, en esta parte se explican los principios
de sus contenidos y los puntos en que se
debe prestar atención durante el desarrollo
de la clase. Los docentes deben entender
la idea central por la cual se desarrolla el
plan de clase.
5 Desarrollo de clase
En este apartado se encuentra descrito
el plan de cada clase usando las páginas
del LE.
Una hora clase equivale a 45 minutos.
Como los niños y las niñas no pueden
concentrarse por mucho tiempo, no es
recomendable prolongar la hora de clase,
salvo en el caso donde ellos hacen una
tarea especial.
Objetivo/Propósito
Representa el objetivo/propósito de la
clase (hay casos donde uno solo se apli-
ca a dos o más clases seguidas). Es muy
necesario tener un objetivo claro para cada
clase.
Materiales
Se indican los materiales didácticos que
se utilizan en la clase. Es recomendable
verlos de antemano, porque hay materiales
que necesitan tiempo para su preparación.
Si se realiza la clase de otra forma a la
explicada en la GM, puede ser que se
necesite otro tipo de material que no esté
indicado. Por ejemplo: una lámina de un
dibujo del LE.
Es necesario saber usar los materiales
(concretos, semiconcretos y abstractos),
ya que la clase no es necesariamente
mejor si se usan más materiales. Es impor-
tante usar aquellos que sean adecuados a
la situación, considerando la etapa del de-
sarrollo mental de los niños y las niñas.
Proceso de enseñanza
El proceso de enseñanza está numera-
do según el proceso del desarrollo de la
clase.
Las etapas principales del proceso son:
1. Introducción
• Repaso
• Presentación del problema (Levanta-
miento de la motivación)
• Previsión de la resolución
2. Desarrollo
• Resolución independiente (o grupal)
• Presentación de ideas
• Discusión y análisis
• Introducción de la nueva regla
3. Conclusión
• Demostración (confirmación) del uso
de la nueva regla
• Ejercicios (reforzamiento)
• Resumen final
• (Tarea)
Este proceso es un patrón que responde
a una clase de introducción, no obstante
dependiendo del tipo de clase algunos de
estos pasos se pueden omitir.
En vez de realizar la clase de la misma
forma, de principio a fin, es deseable
distinguir las actividades de cada etapa
destacando el objetivo específico, de modo
que los niños y las niñas no se aburran.
Además, para que los niños y las niñas
tengan suficiente tiempo para pensar por
sí mismos y resolver los ejercicios, los y las
docentes tienen que darles una explicación

8. Guía para maestros/as - Matemática 20
grado V
de forma precisa y con pocas palabras
tratando de no hablar mucho.
A continuación se explica el significado de
las dos letras utilizadas en el proceso de
enseñanza.
M: significa pregunta o indicación de los y
las docentes a los niños y a las niñas.
Es necesario hacer preguntas interesantes
que despierten el interés de los alumnos
y las alumnas, evitando por tanto aquellas
para responder con palabras breves como
«sí» y «no». Son muy importantes las
preguntas que hacen pensar a los niños
y a las niñas.
RP: significa reacciones previsibles de los
niños y las niñas.
Hay que prever las reacciones de los ni-
ños y las niñas, incluyendo las respuestas
equivocadas. Para corregir las respuestas
equivocadas hay que pensar como piensan
los niños y las niñas, por tanto debemos
evitar decir solamente «está mala», y en-
señar la respuesta correcta o hacer que
contesten otros niños. Hay que dar tiempo
para que piensen el por qué de su respues-
ta hasta descubrir que está equivocada. Al
mismo tiempo, los y las docentes tienen
que pensar por qué se han equivocado y
reflexionar sobre su manera de enseñar y
preguntar. Además, las respuestas de los
niños y las niñas pueden ser indicadores
para evaluar el nivel de entendimiento del
contenido de la lección.
En cuanto al significado de los demás sím-
bolos, consulte a la “Estructura de la Guía
para Maestros y Maestras”.
Para ser más práctico el uso de esta GM
en el aula, se da una descripción general,
por lo tanto, no se les indica a los y las
docentes todas las acciones, así que tie-
nen que agregarlas según la necesidad,
entre las cuales las siguientes se aplican
en general:
1. La GM no dice nada sobre la evaluación
de cada clase, porque ésta corresponde
al objetivo y es fácil de encontrar. La
evaluación debe hacerse durante la
clase y al final de la misma según la
necesidad.
2. En algunos casos, no está indicado el
repaso de la clase anterior, lo que hay
que hacer según la necesidad.
3. Cuando se les dan los problemas o ejer-
cicios, los docentes tienen que recorrer
el aula identificando los errores de los
niños y las niñas y ayudarles a descubrir
el error.
4. Cuando la cantidad de ejercicios es
grande, se hace la comprobación y co-
rrección de errores cada 4 ó 5 ejercicios,
para que los niños y las niñas no repitan
el mismo tipo de equivocación.
5. Preparar tareas, como por ejemplo ejer-
cicios suplementarios, para los niños y
las niñas que terminan rápido.
6. La orientación individual no está indica-
da, sin embargo, es imprescindible. Los
y las docentes pueden realizarla en las
ocasiones siguientes:
• Cuando recorren el aula después
facilitar los ejercicios o problemas.
• En el receso, después de la clase.
• En la revisión del cuaderno (hay que
tener cuidado de que los niños y las
niñas no pierdan tiempo haciendo
colas en filas para que el docente los
corrija)
La manera de cómo trabajar con los
problemas planteados (de aplicación)
Hay 3 elementos fundamentales para re-
solver un problema.
1. Primero escribir el planteamiento de la
operación (PO). Si no se sabe el resulta-
do en ese momento, sólo escribir el lado
izquierdo.
2. Luego efectuar el cálculo, según la
necesidad.
Escribir el resultado del cálculo en el lado
derecho del PO y completarlo.
3. Escribir la respuesta (R) con la unidad
necesaria.
[Ejemplo]
PO: 26+35=61 R: 61 mentas
Primero se juzga que la respuesta se pue-
de encontrar con la adición y escribir el lado

9. Guía para maestros/as - Matemática 20
gradoVI
izquierdo del PO: 26+35. Luego (si no se
puede encontrar la respuesta con el cálculo
mental) efectuar el cálculo, completar el
PO agregando el resultado al lado derecho:
26+35=61. Al final, se escribe la R con la
unidad: 61 mentas.
Siempre se requiere PO y R y hay que
evaluarlos por separado, es decir si está
bien el PO y si está bien la R.
Si algún niño o niña escribe bien el lado
izquierdo del PO: 26+35, pero se equivoca
en el cálculo y contesta así: PO:26+35=51
R: 51 mentas, debe darle 5 puntos si el
total es 10.
La estructura del LE y su uso
Cada unidad empieza con el repaso de lo
aprendido, que tiene que ver con la unidad
(Recordemos). Generalmente, esta parte
no está incluida en las horas de clase y los
docentes asignan el tiempo para trabajar
con el mismo según su criterio.
La unidad está dividida en lecciones, los
ejemplos (A,B,C…) y los ejercicios ( 1 , 2 ,
3 …) están numerados por lección.
Los problemas principales (ejemplos)
corresponden a los temas importantes de
la lección y están ilustrados con dibujos
o gráficas que ayudan a los niños y a las
niñas a entender los ejercicios.
En la orientación de estos ejemplos, lo
importante es hacer que los niños y las
niñas piensen por sí mismos; por lo tanto,
para presentarlos, los docentes los dibujan
en la pizarra para que los niños y las niñas
no vean la respuesta antes de tratar de
encontrarla, aun cuando la GM dice «Leer
el problema…».
Las respuestas de los ejemplos están
marcados con el signo .
La GM lleva la pauta de los ejercicios y
problemas del LE (en color rojo). Los
docentes tienen que tomar en cuenta que
pueden haber otras respuestas correctas.
Los puntos importantes del tema están
marcados con el signo .
Los ejercicios del cálculo están clasifica-
dos por criterios, los cuales pueden ser
consultados en la GM.
Un motivo de este LE es suministrar su-
ficiente cantidad de ejercicios bien clasifi-
cados, por lo tanto, en el LE a veces hay
más ejercicios que se pueden resolver en
el aula. Los docentes tienen que elegir
cierta cantidad de ejercicios de cada grupo
clasificado de modo que los niños y las
niñas puedan resolver todos los ejercicios
tipos. Los demás, se pueden utilizar como
tarea en casa, ejercicios suplementarios
para los niños y las niñas que resuelven
rápido o, en caso de la escuela multigrado,
tarea mientras esperan la indicación del o
la docente.
Por ejemplo: Unidad 4: Resta Lección 3,
la cuarta clase
Según la GM los niños y las niñas trabajan
con los ejercicios 6 y 7 . Los docentes
pueden hacer que resuelvan los primeros
dos o tres ejercicios de cada grupo en el
aula y los demás se pueden utilizar como
tarea en casa.
Hay unidades que tienen «Ejercicios» al fi-
nal, el trabajo con los mismos está incluido
en las horas de clase de la unidad.
Algunas unidades tienen «Ejercicios suple-
mentarios». Se pueden dar a los niños y
a las niñas que trabajan rápido o dejarlos
como tarea en casa.

10. Guía para maestros/as - Matemática 20
grado VII
Ejemplodeldesarrollo
4. Ejemplo del desarrollo de una clase
Vamos a desarrollar una clase, explican-
do dos casos típicos, es decir: la clase
donde se introduce un nuevo concepto o
conocimiento, y la otra donde se hacen
ejercicios sobre el contenido aprendido
para su fijación.
Clase de introducción de un nuevo
tema
Para desarrollar una clase de introducción
de un nuevo tema, además de las suge-
rencias que a continuación se presentan
se recomienda consultar las etapas que
aparecen en “Proceso de enseñanza” de
la pagina IV de esta GM por que tienen
bastante similitud.
1. Preparar una pregunta (un problema)
principal de conformidad con el objetivo
de la clase.
Ésta tiene que ser presentada con tal
motivación que los niños y las niñas ten-
gan ganas de resolverla. Como en el LE
está la respuesta después de la pregunta,
es preferible presentar la pregunta en la
pizarra con los LE cerrados.
2. Ayudar a los niños y a las niñas a resolver
el problema.
Preparar los materiales didácticos que
ayuden a los niños y a las niñas a resolver
el problema.
Dar suficiente tiempo para pensar. Los
niños y las niñas pueden trabajar en forma
individual o en grupo, según la situación.
Dar sugerencias según la necesidad.
3. Los niños y las niñas presentan sus ideas.
Hay que crear la actitud de no tener miedo
a equivocarse, así como la de escuchar las
ideas de sus compañeros. Buscar siempre
otras ideas preguntando: «¿otra?».
4. Los niños y las niñas discuten sobre las
ideas presentadas.
5. Concluir la discusión y presentar la mane-
ra de resolver el problema, aprovechando
las ideas y palabras de los niños y de las
niñas.
6. Evaluar el nivel de comprensión con algu-
nos ejercicios, los que se pueden resolver
aplicando la forma aprendida en clase.
Debemos evitar dar a los niños y a las ni-
ñas los conceptos nuevos, las fórmulas del
cálculo, etc., como cosas ya hechas y sólo
para recordar, porque de esta manera no
se puede crear en ellos la actitud de resol-
ver problemas por su propia iniciativa.
Clase de fijación de lo aprendido re-
solviendo los ejercicios
1. Si los ejemplos contienen algo nuevo (la
forma del cálculo, etc.), hacer que los
niños y las niñas piensen en la forma de
resolverlos con el LE cerrado, como en
el caso de la clase de la introducción de
un nuevo concepto.
2. Después de que los niños y las niñas
entiendan la forma de resolver los
ejercicios, hacerlos trabajar con los
ejercicios de la siguiente manera:
(a) Primero darles cierta cantidad de
ejercicios a la vez y que los resuel-
van individualmente.
(b) Mientras tanto, recorrer el aula y
detectar las deficiencias de los niños
y las niñas.
(c) Después de algún tiempo (cuando
la mayoría ha terminado) mandar a
algunos niños o niñas a la pizarra
para que escriban las respuestas,
todos a la vez (en vez de uno tras
otro); incluyendo las respuestas
equivocadas típicas.
(d) Revisar las respuestas pidiendo
las opiniones de los niños y de las
niñas. No borrar las respuestas
equivocadas, sino marcarlas con X
y corregirlas, o escribir la respuesta
correcta al lado.
(e) Si hay muchos ejercicios, agrupar-
los en varios bloques y seguir el
proceso anterior para que los niños
y las niñas no repitan las mismas
equivocaciones.
Cuando se manda a un solo niño o niña
a la pizarra, se atiende sólo a ese niño o
niña, esto tiene como consecuencia que
no se pueden dar suficientes ejercicios a
los demás, que no están en la pizarra, no

11. Guía para maestros/as - Matemática 20
gradoVIII
M no indica la situación en que los
niños y las niñas deberán pen-
sar por ellos mismos al obser-
var el problema del LE y sólo
está dirigiendo las actividades
sin pedir las ideas.
N sólo repiten y contestan las
preguntas que el M indica.
N leen el PO sólo repitiendo sin
el razonamiento adecuado.
N cuando contaron las mentas
encontraron el resultado, por
eso no les interesa esta acti-
vidad de resolver con los ma-
teriales semiconcretos.
M corrige la equivocación rápida-
mente sin consultar la opinión o
idea de los niños y niñas.
N solamente esperan la explica-
ción de M y la escuchan pasi-
vamente.
Ejemplos de una clase de introducción
Unidad 3 de 2do grado: Suma
Lección 3: Sumemos reagrupando 1ra clase
(a) Sin preparación
M: Hoy vamos a aprender a sumar reagrupando.
Abran la página 30 del LE.
M: Observen que Dany tiene 18 mentas y Angela tiene 14
mentas.
M: Si queremos saber, cuántas mentas tienen entre los
dos; hay dos maneras contando las mentas que tienen
entre los dos y sumándolos. ¿Cómo prefieren?
N: Contándolas.
M: Contémoslas todos en voz alta.
N: Una, dos, tres, cuatro, cinco…treinta y dos.
M: ¿Cuántas mentas hay?
N: 32 mentas.
M: Ahora resolvámoslo con la suma. 18 mentas que tiene
el niño y 14 mentas que tiene la niña se escribe así:
PO: 18 + 14 = 32 (lo escribe en la pizarra)
Leámoslo en voz alta todos juntos. ¡Muy bien!
M: Saquen los azulejos y coloquen en su pupitre; primero
1 azulejo de 10 y 8 azulejos de 1 que equivalen a las
mentas del niño, abajo coloquen 1 azulejo de 10 y 4
azulejos de 1 que equivalen a las mentas de la niña,
ahora júntenlos. ¿Cuánto hay en total?
N: Hay 2 azulejos de 10 y 12 azulejos de 1.
M: Esa respuesta no es correcta, está equivocada.
M: En 12 azulejos hay 1 decena y 2 unidades, entonces
se cambia 10 azulejos de 1 y se pasa al lugar de las
decenas y nos quedan 3 decenas y 2 unidades.
M: (Escribe 18 + 14 con los números en forma vertical en
la pizarra). Observen como se suma con los números;
se empieza por las unidades y se dice:
8 + 4 = 12, se escribe el 2 y se lleva 1 a las decenas,
luego 1 + 1 + 1 = 3 el resultado es 32. La respuesta se
escribe así: (R: 32 mentas).
Actividad Observaciones
pueden pensar bien; por lo tanto, no es
recomendable realizar esta técnica si hay
necesidad de darles muchos ejercicios.
En ambos casos es muy importante garan-
tizar, a los niños y a las niñas, suficiente
tiempo para el aprendizaje activo: pensar,
presentar una idea, discutir y resolver los
ejercicios. Para realizarlo, los docentes no
tienen que hablar mucho, evitando dar la
clase sólo con explicaciones o que con-
testen en coro las preguntas que pueden
contestar con una palabra.pueden contes-
tar con una palabra.

12. Guía para maestros/as - Matemática 20
grado IX
Nota: (M representa al maestro o la maestra)
(N representa a los niños y las niñas)
N contestan automáticamente “sí”
sin darse cuenta de su nivel de
comprensiónpornohaberopor-
tunidad de pensar en el proceso
del cálculo por sí mismos.
M: ¿Entendieron?
N: Sí.
M: Ahora cópienlo en su cuaderno y cuando terminen re-
suelvan los problemas que aparecen en 1 del LE.
[Se ha omitido lo demás]
Siempre hay que tratar de crear
un ambiente de confianza en
que los niños y las niñas con-
testen sin tener temor a equivo-
carse.
M induce a los niños y a las niñas
a pensar por sí mismos obser-
vando la situación de LE.
M orienta a los niños y niñas que
tienen dificultad.
M garantiza el tiempo suficiente
para que todos los niños y ni-
ñas terminen.
M da la oportunidad de exponer
su trabajo incluyendo todas las
maneras que usaron y también
la equivocación.
(b) Con preparación
M: ¿Qué observan?
N: Un niño que tiene 18 mentas y una niña que tiene 14
mentas.
M: Pueden imaginar la situación que plantea el dibujo.
N: Sí, se quiere saber cuántas mentas tienen entre los
dos.
M: ¿Cómo se puede encontrar la respuesta? Ayudémosle
a encontrar el resultado.
N: Ya sé cómo hacer, hay que sumar, etc.
M: ¿Cuál es el PO?
N: PO: 18 + 14
M: ¡Muy Bien! Entonces trabajen individualmente resol-
viendo este problema, pueden usar cualquier manera.
M: (Recorre toda el aula observando con atención el tra-
bajo que realizan los niños y las niñas).
M: (Orienta a los niños y las niñas que tienen dificultad
para calcular 8 + 4 recordándoles que esta manera ya
la aprendieron en 1er grado.)
N: (Los niños y las niñas trabajan en forma individual)
Profe, ya terminé.
M: ¡Muy bien! Entonces si ya terminó encuentre otra ma-
nera de resolver.
N: ¡Ah! Entonces hay otras maneras, voy a encontrarlas.
M: (Pide a unos niños o unas niñas como voluntarios para
que presenten su trabajo)
Actividad Observaciones

13. Guía para maestros/as - Matemática 20
gradoX
Es importante crear la actitud
de aprender a analizar y razo-
nar el trabajo y a escuchar a
los demás.
N estimulan el trabajo de sus com-
pañeros y compañeras.
M corrige los errores pidiendo
las opiniones de los niños de
las niñas.
M representa el respeto y valor
al esfuerzo que hizo el niño o
niña aunque llegó al resulta-
do incorrecto y estimula para
crear la actitud de aprender
cometiendo errores.
N: El (A), yo resolví usando los azulejos. Representé la can-
tidad de 18 y 14; luego sumé las unidades y me dio 12,
como en 12 hay 1 decena y 2 unidades, entonces pasé
la decena a su posición y me quedó 2 unidades; luego
sumé 2 decenas que hay más 1 decena que pasé son 3
decenas; por eso el resultado es 3 decenas y 2 unidades
que es igual a 32 unidades. 18 + 14 = 32.
M: ¿Qué opinan los demás, es correcto?
N: Si. (Aplauden)
M: ¡Muy bien, le felicito!
N: El (B), yo escribí 18 + 14 = 32, pero para sumar des-
compuse los números en decenas y unidades; enton-
ces primero sumé 10 + 10 = 20, después sumé 8 + 4 =
12 y por último sumé los dos resultados 20 + 12 = 32.
M: ¿Qué opinan los demás, es correcto?
N: Si. (Aplauden)
M: ¡Muy bien, le felicito!
N: El (C) yo resolví en la forma vertical, luego empecé a
sumar por las unidades 8 + 4 = 12, escribí 2 y reagrupé 1
y luego sumé las decenas 1 + 1 = 2, por eso me dio 22.
M: ¿Qué opinan los demás, es correcto?
N: El resultado es diferente. Está equivocado. No sumó
lo que reagrupaba, etc.
N: Maestro o maestra, voy a hacer el mío para explicarle
por que se equivocó.
M: Pase ¡por favor! y los demás pongan atención.
N: El mío es el (E), yo también utilicé la forma vertical y
sumé igual que mi compañero, empecé desde las uni-
dades sólo escribí el número que reagrupaba en el lu-
gar de las decenas para que no se me olvidara y luego
sumé lo que reagrupaba y lo que había en las decenas 1
+ 1 + 1 = 3, me dio a 32. Mi compañero o compañera se
equivocó porque se le olvidó sumar lo que reagrupaba.
M: ¿Es correcto?
N: Si. (Aplauden a ambos niños o niñas, el o la que rea-
lizó el (C) con la equivocación y el o la que explicó el
trabajo (E) que sirvió para corregir)
M: ¡Muy bien, les felicito!
M: Pase el o la siguiente a explicar su trabajo de (D).
N: Yo hice igual al anterior, nada más que no escribí el nú-
mero que reagrupaba, pero aprendí que para que no se
me olvide es mejor escribir el número que se reagrupa.

14. Guía para maestros/as - Matemática 20
grado XI
M los motiva y los insta a seguir
adelante.
M confirma el estado de los de-
más.
M los conduce a que decidan con-
juntamente la forma más fácil
rápida para calcular.
M confirma junto con los niños y
las niñas aclarando el proceso
yrecomendandolamejorforma
para evitar el error.
M: ¡Muy bien, les felicito a todos! ¡Excelente trabajo! Son
niños y niñas muy inteligentes, estoy muy orgulloso u
orgullosa de ustedes.
M: Observen todos los trabajos que hicieron, ¿qué opinan?
N: Hay varias maneras de resolver un problema.
M: ¿Quiénes resolvieron con la forma A (B, C, D, E)?
M: ¿Cuál de todas las maneras se les hace más fácil?
N: Creo que el (E), porque las demás formas son iguales
solo que unos usaron los materiales, otros la descom-
posición de los números y otros la forma vertical pero
al final el resultado es el mismo, excepto los o las que
se equivocaron en el cálculo.
M: ¡Muy bien! Entonces vamos a usar la forma vertical de
[E] para calcular. ¿Qué es importante al sumar con el
cálculo vertical?
N: Escribir el número que se reagrupa colocar bien los
números en su posición.
M: ¡Excelente! Vamos a confirmar cómo se hace el cálcu-
lo vertical reagrupando. Hagámoslo todos juntos en el
cuaderno. Primero se escribe:
PO: 18 + 14 = 32 Cálculo vertical
R: 32 mentas.
N: Maestro o maestra hagamos otro ejercicio.
M: ¡Muy bien! Resuelvan los ejercicios 1 del LE.
[Se ha omitido lo demás]
M introduce la clase directamen-
te sin repaso.
M noexplicaelgradodedificultad
que hay entre un tipo y otro.
M (da muy poco tiempo para re-
solver)
Ejemplos de una clase de fijación
Unidad 4 de 2do grado: Resta
Ejercicios (1) 1ra clase
(c) Sin preparación
M: Hoy vamos a realizar ejercicios que aprendieron en la
lección 2.
M: Saquen el LE y busquen la página 47, vamos a resol-
ver los ejercicios de 1 , 2 , 3 y 4 .
M: Resuelvan cada uno en el LE en silencio sin consultar
con su compañero.
N: (Resuelven los ejercicios en el LE).
M: ¿Terminaron?
N: Sí. No maestro o maestra.
Actividad Observaciones

15. Guía para maestros/as - Matemática 20
gradoXII
Se hace el repaso según la
necesidad.
M confirma el contenido que van
a trabajar y busca estrategias
para evitar que los niños y ni-
ñas se equivoquen.
N escuchan con atención la
idea de su compañero o
compañera.
(d) Con preparación
M: La clase de hoy es para confirmar lo que hemos apren-
dido en las 3 clases anteriores, es decir la lección 2.
M: ¿Recuerdan el contenido que vimos en las clases an-
teriores?
N: Aprendimos a restar y a resolver problemas.
M: ¡Muy bien! Entonces en la clase de hoy vamos a desa-
rrollar varios ejercicios para confirmar lo aprendido.
M: Abran su LE en la página 47 y resuelvan el ejercicio [
1 (1)].
M: (Dice a los niños y niñas que cuando terminen levan-
ten la mano y que le miren a su cara en señal que ya
terminaron).
M: (A los niños y niñas que terminaron les indica que pue-
de continuar resolviendo los otros ejercicios y espera
que todos terminen).
N: (Todos los niños y niñas terminaron).
M: (Pasa a un voluntario, niño o niña, a la pizarra para
que resuelva y explique el ejercicio e indica a los de-
más que dejen de trabajar, que coloquen sus lápices
sobre el pupitre y que escuchen la explicación de su
compañero o compañera comparando la forma en que
trabajó cada uno).
N: (Resuelve diciendo el proceso en voz alta; empiezo
por las unidades y digo 5 menos 2 es igual a
3, y luego en las decenas 3 menos 1 es igual
a 2, por eso el resultado de 35 menos 12 es
igual a 23).
M: ¿Es correcto?
N: Sí.
Actividad Observaciones
M manda a los niños y niñas a
la pizarra uno a uno.
M (sólo dirige al niño o niña que
está en la pizarra)
N (esperan que termine el que
está en la pizarra para copiar
después en su LE).
M (no revisa el trabajo que rea-
lizaron los niños y las niñas
en el LE).
M: No importa van a pasar uno a uno a la pizarra.
N: (Un niño o niña pasa a la pizarra)
M: (Pide a un niño o niña que le dicte el primer ejercicio).
N: (Un niño o niña dicta y el niño o niña que está en la
pizarra copia)
N: (Resuelve) Ya terminé maestro o maestra.
M: ¿Está correcto lo que hizo su compañero o compañera?
N: Sí.
M: Pase otro u otra a la pizarra. (Sigue el mismo procedi-
miento hasta terminar todos los ejercicios del LE).
[ Se ha omitido lo demás]

16. Guía para maestros/as - Matemática 20
grado XIII
M evalúaelresultadoobtenidode
cada niño y niña, y da la orien-
tación general para los y las
que se equivocaron analizan-
do las causas conjuntamente.
M da la oportunidad para que to-
dos trabajen individualmente.
N trabajan en forma individual.
M presta atención al trabajo que
realizan y hace la orientación
individual a los niños y niñas
que tienen dificultad.
M aprovecha el tiempo enviándo-
los a resolver al mismo tiempo.
M indica la forma de corregir
los errores (uso del lápiz co-
lor rojo).
N estimulan el trabajo que rea-
lizaron sus compañeros y
compañeras.
M verifica si los niños y niñas entien-
den muy bien las instrucciones.
M confirma los puntos impor-
tantes para evitar la posibili-
dad del error.
M da participación democrática
a todos los niños y niñas pa-
sando a la pizarra a los que
todavía no lo han hecho.
M confirma si todos los niños y
niñas hicieron su trabajo y a
la vez verifica si aprendieron
muy bien o si necesita refor-
zar algún punto.
M: ¿Levanten la mano a los que les dio este mismo resul-
tado? Los niños y niñas que se equivocaron corrijan
tal como está en la pizarra.
N: Maestro o maestra, ¿hago el siguiente ejercicio?
M: Primero quiero que los resuelvan en el LE y después
van a pasar a la pizarra.
N: (Resuelven los ejercicios restantes en el LE).
M: (Observa el trabajo individual de los niños y de las ni-
ñas y da el tiempo necesario).
M: ¿Terminaron?
N: Sí.
M: (Manda a un niño o niña por cada ejercicio a la vez).
N: (Cada niño o niña explica su trabajo para confirmar si
resolvió correctamente juntos con todos)
M: Comparen su trabajo con el de la pizarra, por favor no
borren el ejercicio equivocado, solo corríjanlo usando
lápiz de otro color.
M: ¡Muy bien, les felicito por su trabajo!
N: (Aplauden a sus compañeros y compañeras)
M: (Indica que van a resolver los ejercicios de 2 , 3 y
4 del LE).
M: Observen el tipo 2 . ¿Cómo lo van a resolver?
N: Hay que cambiarlo a la forma vertical.
M: Cuando se cambia a la forma vertical ¿qué hay que
tener en cuenta?
N: La colocación de los números, se debe escribir unidad
bajo unidad y decena bajo decena.
M: En los ejercicios del tipo 3 . ¿Qué hay que hacer?
N: Hay que resolver problemas.
M: ¿Qué se hace para resolver problemas?
N: Analizar con qué operación se puede resolver, escribir el
PO, hacer el cálculo y escribir la respuesta con la unidad.
M: ¿Y en los ejercicios del tipo 4 qué van a hacer?
N: Inventar problemas con cada PO.
M: ¡Muy bien! Creo que entendieron lo que van a hacer.
M: Entonces resuélvanlos primero en su LE y cuando to-
dos hayan terminado van a pasar a la pizarra.
M: (Observa el trabajo de los niños y niñas haciendo las
aclaraciones necesarias para los que tienen dificultad).
M: (Da la indicación para los que terminen primero).
M: (Manda a la pizarra a varios niños y niñas a la vez para
que presenten el trabajo que hicieron).
M: (Al final revisa chequeando el trabajo de cada uno de
los niños y niñas en el LE).
[se ha omitido lo demás]

17. Guía para maestros/as - Matemática 20
gradoXIV
NOVIEMBREOCTUBREAGOSTO/SEPTIEMBRE
(Total 112 horas)
Programación anual
1. Números hasta 999
(15 horas)
Mes
Unidad
(Horas)
Expectativas de logro Contenidos
Pág. de GM
(Pág. de LE)
• Aplican el concepto de
posición de unidades
como ayuda para cons-
truir números grandes
con un conjunto limitado
de símbolos.
• Forma de leer escribir 100.
• Sentido de la centena.
• Forma de contar los números de tres cifras.
• Forma de leer y escribir los números de tres
cifras (sin 0).
• Forma de leer y escribir los números de tres
cifras (con 0).
• Composición de los números de tres cifras.
• Descomposición de los números de tres cifras.
• Representación de los números de tres cifras
en la recta numérica.
• Sucesión y orden ascendente y descendente
de los números de tres cifras.
• Símbolos «>» y «<».
• Comparación de los números de tres cifras.
• Orden de los números (números que están en-
tre dos números).
• Decenas próximas y centenas próximas.
2 – 23
(2 – 19)
2. Números ordinales
(2 horas)
• Usan números ordinales
para describir situaciones
de su vida cotidiana.
• Los números ordinales del 11º hasta 20º. 24 – 27
(20 – 21)
3. Suma
(18 horas)
• Aplicando el concepto de
adición calculan sumas
donde los sumandos son
menores que 100, sin re-
agrupar y reagrupando
• Resuelven problemas
de la vida cotidiana que
implican la adición cuyos
sumandos sean menores
que 100, sin reagrupar y
reagrupando.
• Operación del tipo D0+D0.
• Operación del tipo D0+U.
• Operación del tipo U+D0.
• Operación del tipo DU+DU, sin reagrupar.
• Operación del tipo D0+DU y DU+D0, sin
reagrupar.
• Operación del tipo DU+U, sin reagrupar.
• Operación del tipo U+DU, sin reagrupar.
• Aplicación y dominio de la lección 2.
• Operación del tipo DU+DU, reagrupando.
• Operación del tipo DU+DU=D0, reagrupando.
• Operación del tipo DU+U, reagrupando.
• Operación del tipo U+DU, reagrupando.
• Operación del tipo DU+DU=CDU, reagrupan-
do una vez.
• Operación del tipo DU+DU=CDU, reagrupan-
do dos veces.
28 – 49
(22 – 39)
4. Resta
(15 horas)
• Realizan sustracciones
donde el minuendo es
menor que 100.
• Resuelven problemas de
la vida cotidiana aplican-
do resta con minuendo
menor que 100, sin re-
agrupar y reagrupando.
• Operación del tipo D0–D0=D0.
• Operación del tipo DU–D0=U.
• Operación del tipo DU–U=D0.
• Operación del tipo DU–DU=DU sin reagrupar,
forma vertical.
• Operación de DU–DU=U y DU–U=DU sin re-
agrupar, forma vertical.
• Forma de resolver problemas y su procedi-
miento.
• Operación del tipo DU–DU=DU reagrupando.
• Operación del tipo D0–DU=DU reagrupando.
• Operación del tipo DU–DU=U y D0–DU=U
reagrupando.
50 – 69
(40 – 55)

18. Guía para maestros/as - Matemática 20
grado XV
MARZOFEBREROENERODICIEMBREMes
Unidad
(Horas)
Expectativas de logro Contenidos
Pág. de GM
(Pág. de LE)
• Operación del tipo DU–U=DU y D0–U=DU
reagrupando.
• Ejercicios de toda la unidad.
5. Suma y resta combi-
nadas
(6 horas)
• Resuelven situaciones
de la vida cotidiana que
implican adiciones y sus-
tracciones combinadas.
• Planteamiento de la operación y cálculo de su-
mas sucesivas.
• Planteamiento de la operación y cálculo de
restas sucesivas.
• Planteamiento de la operación y cálculo de su-
mas y restas combinadas.
70 – 77
(56 – 61)
6. Figuras geométricas
(4 horas)
• Identifican el concepto de
triánglo y cuadrilátero.
• Idea de línea recta.
• Concepto de triángulo y cuadrilátero.
• Construcción de triángulos y cuadriláteros.
78 – 85
(62 – 67)
7. Multiplicación
(35 horas)
• Construyen el concepto
de multiplicación como
abreviación de la adición
de sumandos iguales.
• Desarrollan las tablas de
la multiplicación del 1 al 9.
• Resuelven problemas de
la vida real aplicando la
multiplicación.
• Sentido de la multiplicación.
• Escritura del signo de la multiplicación.
• Planteamiento de la operación de la multi-
plicación.
• Cálculo del producto utilizando adiciones
sucesivas.
• Términos “factores” “producto”.
• Construcción de la tabla del 2.
• Memorización y aplicación de la tabla del 2.
• Construcción de la tabla del 5.
• Memorización y aplicación de la tabla del 5.
• Construcción de la tabla del 3.
• Memorización y aplicación de la tabla del 3.
• Construcción de la tabla del 4.
• Memorización y aplicación de la tabla del 4.
• Práctica y dominio de las tablas del 2 al 5.
• Construcción de la tabla del 6.
• Memorización y aplicación de la tabla del 6.
• Construcción de la tabla del 7.
• Memorización y aplicación de la tabla del 7.
• Construcción de la tabla del 8.
• Memorización y aplicación de la tabla del 8.
• Construcción de la tabla del 9.
• Memorización y aplicación de la tabla del 9.
• Práctica y dominio de las tablas del 6 al 9.
• Construcción y memorización de la tabla del 1.
• Construcción y lectura de la tabla de la multipli-
cación de dos dimensiones.
• Regla entre el segundo factor y el producto.
• Propiedad conmutativa de la multiplicación.
• Práctica y dominio de todas las tablas.
86 – 123
(68 – 97)
8. Longitud
(8 horas)
• Aplican las unidades de
centímetro, decímetro y
metro del sistema métrico
decimal en la medición de
longitudes.
• Miden la longitud de obje-
tos de su entorno con una
regla graduada y cinta
métrica.
• Necesidad y utilidad de las unidades oficiales.
• Unidad oficial del sistema métrico decimal “el
metro”.
• Construcción de la regla de 1 metro.
• Medición de la longitud usando “el metro”.
• Unidades oficiales del sistema métrico decimal
“el centímetro” y “el decímetro”.
• Relación entre las unidades oficiales (1 dm =
10 cm).
• Medición de la longitud usando “el centímetro”.
124 – 133
(98 – 105)

19. Guía para maestros/as - Matemática 20
gradoXVI
ABRIL
Distribución de horas en cada bloque
Mes
Unidad
(Horas)
Expectativas de logro Contenidos
Pág. de GM
(Pág. de LE)
• Estiman longitudes usan-
do las unidades de metro,
decímetro y centímetro.
• Uso de la medición para trazar línea recta.
• Relación entre las unidades oficiales (1 m = 10
dm, 1 m = 100 cm).
• Escritura de la longitud usando la tabla de po-
sición de unidades (m, dm y cm).
• Medición de la longitud con las unidades oficiales.
• Estimación de la longitud usando el metro, de-
címetro y centímetro.
Bloque
1. Números y operaciones
2. Geometría
3. Medidas
4. Estadística
Unidades
1, 2, 3, 4, 5, 7
6
8, 10, 11
9
Horas
91
4
16
2
9. Estadística
(2 horas)
• Recopilan y clasifican da-
tos proporcionados pre-
viamente.
• Organizan y distribuyen
datos estadísticos en ta-
blas o cuadros.
• Interpretan pictogramas.
• Recolección de datos.
• Clasificación, conteo y organización de datos.
• Distribución de datos en una tabla.
• Interpretación de pictogramas.
134 – 139
(106 – 109)
10. Tiempo
(5 horas)
• Desarrollan el concepto
de tiempo.
• Identifican unidades de
tiempo (minuto, hora, día,
semana, mes, año) en la
medición de la duración
de diversos eventos, pro-
cesos o actividades.
• Leen la hora en punto y la
hora y minuto en reloj de
aguja y digital.
• El mecanismo y el papel del reloj de aguja.
• Lectura y representación de la hora en punto y
hora y minutos.
• Concepto del tiempo.
• Unidades de tiempo (minuto y hora).
• Unidades oficiales de tiempo (día, semana,
mes y año).
• Determinación de la fecha y el tiempo con el
calendario.
140 – 149
(110 – 115)
11. Moneda nacional
(3 horas)
• Identifican monedas y bille-
tes de circulación nacional.
• Establecen equivalencias
del peso dominicano con
monedas y billetes de cir-
culación en nacional.
• Utilizan monedas y bille-
tes en situaciones de la
vida diaria.
• Identificación de los billetes de 100, 200 y 500
pesos.
• Equivalencia entre monedas y billetes hasta
500 pesos.
• Resolución de problemas de la vida diaria
usando el dinero de circulación nacional.
150 – 155
(116 – 119)
total 113
MAYO

21. Unidad 1 - Números hasta 9992
1
11
• Aplican el concepto de posición de unidades como ayuda para construir números grandes con un
conjunto limitado de símbolos.
Números hasta 999
Expectativas de logro
(15 horas)Unidad
Números hasta 999
• Concepto de «centena».
• Leer, escribir y construir
el significado de los
números hasta 999.
• Composición y descom-
posición de números de
tres dígitos.
• Representar números
de tres dígitos en la
recta numérica.
• Orden de números de
tres dígitos.
• Comparar números de
tres dígitos.
Números hasta 9,999
• Concepto de «unidad
de mil».
• Leer, escribir y construir
el significado de los
números hasta 9,999.
• Composición y descom-
posición de números de
cuatro dígitos.
• Representar números
de cuatro dígitos en la
recta numérica.
• Orden de números de
cuatro dígitos.
• Comparar números de
cuatro dígitos.
Números hasta 1,000,000
• Concepto de «decena
de mil», «centena de
mil».
• Leer, escribir y construir
el significado de los nú-
meros hasta 1,000,000.
• Composición y descom-
posición de números
hasta 1,000,000.
• Representar números
hasta 1,000,000 en la
recta numérica.
• Orden de números
hasta 1,000,000.
• Comparar números
hasta 1,000,000.
• Redondeo de números.
• Numeración romana.
Relación de objetos y
elementos
Grupos de objetos y
elementos
Relación y desarrollo2
Números hasta 9
• Leer, escribir y construir
el significado de los
números del 1 al 9.
• Concepto del cero (0).
• Orden de números del
cero al 9.
• Composición y descom-
posición de números
entre 1 y 9.
Números hasta 19
• Concepto de «unidad» y
«decena».
• Composición y descom-
posición del número 10.
• Leer, escribir y construir
el significado de los
números hasta 19.
• Representar números
hasta 19 en la recta
numérica.
Números hasta 99
• Leer, escribir y construir
el significado de los
números hasta 99.
• Orden de números
hasta 99.
• Contar en grupo de 2, 5
y 10.

22. Guía para maestros/as - Matemática 20
Grado 3
4 Puntos de lección
• Lección 1: Conozcamos la centena
Se dirige a los niños y a las niñas la forma
de generar el concepto de los números des-
de 100 al 999 y la manera de contar, leer y
escribir a través de las actividades de contar
grupos de materiales concretos y semicon-
cretos. También que ellos experimenten la
conveniencia de contar haciendo grupos de
10 y que capten que la cantidad de 1 + 99 y
la cantidad de 10 grupos de 10 son iguales, o
sea que una centena se compone de 100 uni-
dades ó 10 decenas a través del manejo con
los materiales concretos y semiconcretos.
En cuanto al uso de los azulejos (un tipo de
materiales semiconcretos), véase Columnas.
• Lección 2: Leamos y escribamos
números
Se orienta el principio del valor posicional y la
escritura de los números de tres cifras. Me-
diante la analogía con los números de dos ci-
fras y el conteo del material concreto o semi-
concreto se espera que los niños y las niñas
descubran la escritura de los números de tres
cifras y se den cuenta del principio del valor
posicional en el mecanismo de la numeración
decimal (tanto en grupos de 10 como en gru-
pos de 100) y la conveniencia de utilizarlo, de
manera que puedan aplicarlo a los números
más grandes. La actividad de contar haciendo
grupos es muy útil para la comprensión de la
1/2 • Forma de leer escribir 100
3 Plan de estudio (15 horas)
1. Conozcamos la centena
(2 horas)
1/6~2/62. Leamos y escribamos
números
(6 hora)
• Forma de contar los números de tres cifras
2/2 • Sentido de la centena
1/23. Ordenemos números
(2 horas)
• Representación de los números de tres cifras en la
recta numérica
2/2 • Sucesión y orden ascendente y descendente de los
números de tres cifras
1/54. Comparemos números
(5 horas)
• Símbolos «>» y «<»
3/6 • Forma de leer y escribir los números de tres cifras
(sin 0)
4/6 • Forma de leer y escribir los números de tres cifras
(con 0)
5/6 • Composición de los números de tres cifras
6/6 • Descomposición de los números de tres cifras
2/5 • Comparación de los números de tres cifras
3/5 • Orden de los números (números que están entre
dos números)
4/5~5/5 • Decenas próximas y centenas próximas

23. Unidad 1 - Números hasta 9994
composición de los números, el mecanismo
de la numeración decimal y la comparación
de la dimensión y la sucesión de los núme-
ros. Por lo tanto es necesario que los niños y
las niñas tengan suficiente experiencia para
practicarla.
Acerca de la lectura y escritura de los números
de tres cifras es necesario enseñar a los niños
y a las niñas dando importancia a la relación
entre: la cantidad, el número y la palabra (lec-
tura). Hay posibilidad de tener dificultad en la
escritura del número cuando son mayores o
cuando hay vacante con 0 (por ejemplo: 203).
Una de las causas de este error es cuando no
se pueden relacionar adecuadamente las ex-
presiones con los materiales semiconcretos,
con la palabra y con el número. Por lo tan-
to, para la representación del número con los
materiales, primero se utilizan los azulejos, y
luego otros materiales semiconcretos que tie-
nen el mismo tamaño y diferente color según
la posición y después los del mismo tamaño
y color para que se fijen claramente que cada
posición tiene diferente valor. Así con la direc-
ción progresiva se cultiva un mejor entendi-
miento del valor posicional.
La composición y descomposición se trata
con el acompañamiento de la manipulación
de los materiales concretos o semiconcretos.
• Lección 3: Ordenemos números
El orden y la sucesión de los números se en-
seña antes de la comparación de la dimen-
sión tomando en cuenta que es más fácil para
la comprensión de los niños y las niñas. Es re-
comendable reforzar la enseñanza haciendo
hincapié en el lugar donde cambia la cifra de
un valor posicional, porque es aquí donde los
niños y las niñas sienten más dificultades.
Se utiliza la recta numérica para que los niños
y las niñas aprendan el orden y la sucesión al
observar la posición de los números.
Además se hace para que capten visualmen-
te la relación de la dimensión de éstas, como
un modelo para que ellos aprendan a juzgar
la dimensión de los números en un momento.
El rango de importancia de la recta numérica
aumenta acompañado con la expansión del
mundo numérico. Por lo que es necesario que
se acostumbren a utilizarla.
• Lección 4: Comparemos números
En esta lección los niños y las niñas juzgan la
dimensión de los números de tres cifras. Para
esto se hace que ellos se den cuenta que no
es necesario comparar todos los dígitos sino
que se puede comparar desde los dígitos de la
posición superior.
Al introducir la aproximación la decena próxi-
ma y la centena próxima, se utiliza la recta nu-
mérica para facilitar la visualización de la dis-
tancia hasta la decena, centena próxima. Es
necesario usar estas expresiones en varias
ocasiones en la vida escolar de modo que los
niños y las niñas se acostumbren a la aproxi-
mación y que tengan suficiente habilidad fun-
damental para el estudio del redondeo.

24. Guía para maestros/as - Matemática 20
Grado 5
Azulejos
En esta unidad principalmente se utilizan los azulejos para la comprensión del valor posicional. Los
niños y las niñas pueden utilizar los presentados en las páginas para recortar. Para el maestro o la
maestra, es recomendable que los prepare para la pizarra con el tamaño ampliado en cartulina o car-
toncillo.
Su mayor ventaja es que sirven mucho en la representación del mecanismo del valor posicional decimal
sin perder la percepción de la cantidad (porque mantienen la dimensión de la cantidad en su tamaño).
Por lo tanto, se utilizan más en la orientación del cálculo vertical, principalmente con los números de
dos cifras (se usarán en las unidades de suma y resta en este grado).
0931 2 . . . .
Los materiales didácticos
Tarjetas numéricas
En esta guía no se usan las tarjetas numéricas en este momento para evitar usar demasiados materia-
les pero sí en el 3er grado. Sin embargo, puede introducirlas dentro de esta unidad con los números de
tres cifras desarrollando el mismo papel de los azulejos en la representación de la cantidad.
Tarjetas numerales
Son las tarjetas con los números de 0 a 9. Este material sirve sobre todo para afianzar la comprensión
del concepto de números mediante las prácticas. Se puede inventar varios usos dependiendo del ob-
jetivo de la práctica.
2 3 4
C D Udecena unidadcentena
110100
2
100 10
100
10
10
1
1
1
1
3 4
C D Ucentena decena unidad
Columnas
A
B
C

25. Unidad 1 - Números hasta 9996
5
1. Comentar lo observado en
el dibujo. [A]
2. Contar la cantidad de ove-
jas. [A1]
M: ¿Cuántas ovejas hay? ¿Cómo
las contaron?
RP: 99 ovejas. Las conté hacien-
do grupos de 10.
* Sería recomendable usar la
lámina de 99 ovejas (puede
ser los círculos etc. en vez de
ovejas) para que los niños y
las niñas confirmen la forma de
contar y la cantidad de ovejas.
* Confirmar la cantidad contando
todos juntos, del 1 al 90 de 10
en 10, y del 91 al 99 de 1 en 1.
3. Conocer el número 100 y su
escritura. [A2]
M: (Demostrando la situación en
la pizarra) Está llegando una
oveja más. ¿Cuántas ovejas
hay ahora?
* Explicar que la cantidad que
es 1 más que 99 se llama cien
y se escribe 100 con números.
No es necesario mencionar
sobre la caja de valor ni la
posición de las centenas en
este momento.
* Hacer que cuenten de nuevo
las ovejas, del 1 al 90 de 10 en
10, y del 91 al 100 de 1 en 1.
4. Confirmar la cantidad 100 y
su escritura. [A3]
* Indicar que dibujen círculos en
el cuaderno contando con la
voz baja.
* Realizar un ejercicio de formar
100 usando los azulejos (véa-
se Notas).
5. Resolver el ejercicio 1 .
* Explicar las instrucciones
usando el ejemplo.
Conozcamos la centena
• Leer y escribir el número 100.
Lección 1:
(1/2)
Objetivo:
Materiales:
Desarrollo de
clases
(M) dibujo de 99 ovejas y 1 oveja, azulejos
(N) azulejos
Unidad 1
2 dos
Números hasta 999999
Recordemos
1. Escriba con números cuántos hay.
2. Escriba "treinta y dos" con números.
3. ¿Qué número está formado por 7 decenas y 1 unidad?
4. En cada pareja de números encierra el mayor.
(1) 9 90 (2) 13 25 (3) 62 59 (4) 47 46
(1) (2) 10 10 10 10 1010
Lección 1: Conozcamos la centena
A Observe y conteste. 1 ¿Cuántas ovejas hay en el corral?
2 Está llegando una oveja más. ¿Cuántas ovejas hay por todo?
UD
Diez Trece
3 Escriba cinco veces el número 100.
1 Haga los ejercicios siguiendo las instrucciones.
1: Contar los objetos de cada dibujo y escribir el número.
2: Agregar dibujos (pueden ser círculos) hasta que sean cien y escribir el número cien.
(1) (2) (3)(Ejemplo)
97 100
100
99 1
Hay 99 en el corral más 1 (una)
fuera y forman cien (100)
99 + 1 = 100
56 60
71
32
99
99 100 91 100 94 100
(1/2)
100 100 100 100 100

26. Guía para maestros/as - Matemática 20
Grado 7
Conozcamos la centena
• Aprender el concepto de la centena.
Lección 1:
(2/2)
Objetivo:
Materiales: (M) habichuelas, azulejos
(N) habichuelas, azulejos
1. Captar el tema. [B]
Observando el dibujo que cap-
ten que van a contar las habi-
chuelas haciendo grupos. Cada
niño o niña debe tener más de
100 granos de habichuela u
otro material disponible.
2. Contar 100 objetos hacien-
do grupos de 10.
M: Vamos a contar 100 habichue-
las. ¿Cómo sería mejor para
contar? ¿Por qué?
RP: Haciendo grupos de 10. Por-
que es más fácil de ver y se
puede repetir el conteo de 10
en 10 rápidamente.
* Conducir que cuenten hacien-
do grupos de 10.
* Puede hacer que trabajen en
equipo. Puede hacer que cuen-
ten no solo las habichuelas
sino también otros objetos.
3. Aprender el concepto de las
centenas.
M: ¿Cuántos grupos de 10 formó
para ser 100?
RP: 10 grupos de 10.
M: ¿Cuántas decenas equivalen
a 100 unidades?
RP: 10 decenas.
* Pegar en la pizarra 10 dece-
nas de una representación
de azulejos y confirmar que
equivalen a 100 unidades.
* Introducir el término “la centena”
presentando un azulejo de una
centena y demostrando que su
tamaño es igual a 10 decenas.
4. Confirmar la relación entre las
unidades, decenas y centenas.
* Preguntar sobre las relaciones
entre las tres, por ejemplo,
¿Cuántas decenas hay en 1
centena? ¿Cuántas decenas
hay en 100 unidades? etc.
5. Resolver los ejercicios del
2 al 4 .
3tres
B Cuente 100 objetos formando grupos.
2 Escriba en la línea los números que corresponden.
Juan formó 10 grupos de 10 y forman 100 unidades.
Cada flor tiene ______ pétalos y hay ______ flores. Hay ______ pétalos en total.
3 Encierre objetos que representan 1 centena.
4 Escriba en cada línea el número que corresponde.
A B C D E F G
10 decenas es igual a
100 unidades.
100 unidades forman una
1 centena.
10 decenas
(1) 1 centena = ________ decenas (2) 100 unidades = ________ decenas
(3) 100 unidades = ________ centena (4) 10 decenas = ________ centena
(5) 10 decenas = ________ unidades (6) 1 centena = ________ unidades
100 unidades
1 centena
=
10
10 10
100 100
1 1
10 100
(2/2)
Puede usar varias formas para llegar a la centena. Aquí
en esta guía hemos priorizado el sistema de numera-
ción decimal (agrupando de 10 en 10).

27. Unidad 1 - Números hasta 9998
1. Captar el tema. [A]
2. Estimar la cantidad de los
pollitos.
M: ¿Cuántos pollitos creen que
hay en el patio más o me-
nos?
RP: Unos 100. Más de 100.
* Mediante la estimación elevar
el entusiasmo para contar.
* Aclarar bien que solo son los po-
llitos del patio, no del gallinero.
3. Contar la cantidad de pollitos.
M: Vamos a contar los pollitos
que hay en el patio pensando
la manera más fácil y sin equi-
vocarse.
Que recuerden la forma de
contar haciendo grupos.
* Se puede hacer que trabajen
en equipo.
* Recorriendo el aula, apoyar a
los niños y las niñas que no
se dan cuenta de contar for-
mando grupos de 10. También
apoyar a los que cuentan for-
mando 10, preguntando qué
se puede hacer cuando hay
muchos grupos de 10.
Continúa en la siguiente página…
Leamos y escribamos números
• Contar los números de tres cifras haciendo grupos de
10 y grupos de 100.
Lección 2:
(1/6~2/6)
Objetivo:
Materiales: (M) habichuelas, azulejos
(N) habichuelas, azulejos
R
9
9
9
9 9 9
R
!Cuantos pollitos!
¿Habrá más de
cien o no?
4 cuatro
Lección 2: Leamos y escribamos números
A Cuente cuántos pollitos hay en el patio.
(1/6~2/6)

28. Guía para maestros/as - Matemática 20
Grado 9
… viene de la página anterior
4. Expresar la forma de contar
y la cantidad de pollitos.
M: ¿Cuántos pollitos hay? ¿Cómo
contaron?
Que comparen la forma de
contar con los compañeros y
compañeras.
* Designar la participación de
cada niño o niña (grupo) co-
menzando por aquellos donde
se observó que contaron de
la forma más sencilla (por
ejemplo, contaron de 1 en 1)
y terminar con los que tuvieron
la idea más cercana al objetivo
de esta clase (por ejemplo,
contaron de 10 en 10 y forma-
ron grupos de 10 decenas).
Continúa en la siguiente página…
Leamos y escribamos númerosLección 2:
(1/6~2/6)
[Continuación]
5cinco
9
9
GallineroGallinero
9 9

29. Unidad 1 - Números hasta 99910
[Ejemplo 2 de la práctica]
1: Formar pareja y sentarse frente a frente.
2: Alguno de los dos hace las palmadas (de 1 hasta 9 veces).
3: Otro escucha la cantidad de palmadas o dice la cantidad con-
tando una centena por cada palmada. Por ejemplo, con cuatro palma-
das se dice “cuatrocientos”.
4: Al siguiente turno cambiarán los papeles.
* Puede hacer que pregunten mutuamente en vez de la palmada, por
ejemplo, “Hay 3 centenas. ¿Cómo se dice este número?”.
… viene de la página anterior
5. Confirmar la cantidad de po-
llitos.
* Aprovechando las opiniones
de los niños y las niñas con-
firmar que hay 2 centenas de
pollitos en el patio, y se dice
doscientos.
6. Conocer la forma de decir las
cantidad de 100 en 100 y prac-
ticar el conteo.
* Explicar cómo se dice y escri-
be con los números desde 1
centena hasta 9 centenas.
* Hacer que los niños y las niñas
digan juntos desde 100 hasta
900 a un buen ritmo.
[Ejemplo 1 de la práctica]
1: Formar pareja y sentarse
frente a frente.
2:Alguno de los dos dice “cien”
levantándose de su puesto.
3: Otro dice “doscientos”,
levantándose de su puesto
mientras el otro se sienta.
4: Seguir contando hasta “no-
vecientos” alternándose uno
con otro.
5: Pueden continuar contando
sin parar al decir “cien” des-
pués de “novecientos”.
* Si se comete un error o tarda
demasiado tiempo para decir
la cantidad se pierde. También
se puede jugar en grupo.
[Ejemplo 2 de la práctica]
Véase Notas.
7. Resolver el ejercicio 1 .
Continúa en la siguiente página…
Leamos y escribamos númerosLección 2:
(1/6~2/6)
[Continuación]
Se forman 2 centenas.
Hay doscientos pollitos en el patio.
1 Una con líneas el dibujo y las palabras correspondientes.
7 centenas
3 centenas
1 centena
5 centenas
cien
setecientos
quinientos
trescientos
6 seis
1 centena cien
2 centenas doscientos
3 centenas trescientos
5 centenas quinientos
6 centenas seiscientos
7 centenas setecientos
8 centenas ochocientos
9 centenas novecientos
4 centenas cuatrocientos

30. Guía para maestros/as - Matemática 20
Grado 11
… viene de la página anterior
8. Contar todos los pollitos. [B1]
M: Vamos a contar cuántos pollitos
hay por todo. ¿Cómo hacemos?
Que se den cuenta que se
puede contar los pollitos que
están en el gallinero y luego
unir con doscientos pollitos
que habían contado.
* Indicar que cuenten los pollitos del
gallinero formando grupos de 10.
9. Confirmar la cantidad total
de pollitos.
M: ¿Cuántas centenas, cuántas
decenas y cuántas unidades
de pollitos hay por todo?
RP: 2 centenas, 3 decenas y 6
unidades de pollitos.
M: ¿Cómo podríamos llamar esta
cantidad?
RP: 2 centenas se dice doscientos,
3 decenas y 6 unidades se dice
treinta y seis, entonces en total
son doscientos treinta y seis.
Que descubran el numeral
aplicando lo aprendido.
10.Practicar la forma de contar
y decir los números de 3 ci-
fras. [B2]
* Explicar el juego de quién aga-
rra más habichuelas (puede
ser granos de maíz) con las
dos manos. Indicar que cada
vez que termina de contar,
escriban el resultado en el
cuaderno de forma “tantas
centenas, tantas decenas y
tantas unidades”.
11. Resolver el ejercicio 2 .
A los niños y a las niñas de segundo grado, todavía les
cuesta escribir las letras y por eso tardan mucho tiem-
po. Por lo tanto para desarrollar suficiente cantidad de
ejercicios en la clase se puede omitir la actividad de escribir
la cantidad con palabras, sólo que ellos digan el número formado
por “tantas centenas, tantas decenas y tantas unidades”.
Leamos y escribamos númerosLección 2:
(1/6~2/6)
[Continuación]
B1 Observe el dibujo de A.
¿Cuántos pollitos hay por todo?
2 Juegue contando las habichuelas.
[¿Quién agarra más?]
2 Cuente los sorbetes y los azulejos. Escriba el número correspondiente en
la casilla y la cantidad en palabra en la línea.
7siete
2 centenas en el patio, 3 decenas y 6 unidades en el gallinero.
doscientos treinta y seis
Hay doscientos treinta y seis pollitos por todo.
1 centena, 6 decenas, 9 unidades
ciento sesenta y nueve
2 centenas, 1 decena, 5 unidades
doscientos quince
(1) (2)
(3) (4)
R.
centenas
decenas
unidades
R.
R.
R.
100
100
10
100
100
10
10
centenas
decena
unidades
Ganador
centenas
decenas
unidades
centenas
decena
unidades
2
2
5
5
3
8
2
1
3
1
9
7
Doscientos veinticinco Doscientos trece
Quinientos treinta y ocho Ciento noventa y siete
[Hasta aquí 1/6]
[Desde aquí 2/6]

31. Unidad 1 - Números hasta 99912
1. Comentar lo observado. [C]
Que sientan la necesidad de
ordenar.
2. Ordenar los azulejos.
M: ¿Qué hacemos para contarlos
fácilmente?
RP: Ordenándolos. Agrupándolos
por el mismo tamaño, etc.
* Colocar los azulejos de la for-
ma siguiente:
M: ¿Está bien así? ¿Por qué?
RP: No está bien. Porque el valor ya
está decidido en la tabla de valo-
res. Porque hay que colocarlos
desde el pequeño hasta el gran-
de, de derecha a izquierda.
Que cuenten el principio del
valor posicional con sus pro-
pias palabras (véase Notas).
3. Pensar en la forma de escribir
los números de tres cifras.
M: ¿Cómo se escribiría “doscientos
treinta y seis” con los números?
Que encuentren la respuesta
aplicando el valor posicional
de los números de 2 cifras.
* Designar algunos niños y niñas
para que expresen sus ideas.
4. Concluir la forma de escribir
los números de tres cifras.
Que pronostiquen que si hay
10 grupos de centenas tendrán
otra posición a la izquierda de
la centena y que esta situación
se repite para los números
mayores. También que se den
cuenta que se puede escribir
sólo un dígito, desde 0 hasta
9, en una posición.
5. Resolver los ejercicios del
3 al 5 .
Leamos y escribamos números
• Leer y escribir los números de tres cifras (sin 0) apli-
cando lo aprendido en la posición decimal de los nú-
meros de dos cifras.
Lección 2:
(3/6)
Objetivo:
Materiales: (M) azulejos
(N) azulejos
Hay posibilidad de encontrar entre las opiniones de los
niños y las niñas que ya hay una regla para colocar las
unidades y las decenas, reflexionando el estudio de 1er
grado. Al preguntarles por qué hay que colocar las centenas
a la izquierda de las decenas y no a la derecha de las unidades, se
espera que los niños y las niñas se den cuenta del principio del valor
posicional, por ejemplo, si hay grupos de 10 hay que pasarse al lado
izquierdo, los grupos más grandes se van al lado izquierdo, etc.
C Piense cómo se escribe con números la cantidad de pollitos
(doscientos treinta y seis).
8 ocho
3
4
5
Tal vez
ordenando
un poco más...
Escriba con números cuántos hay y léalos.
(3) 9 centenas, 6 decenas y 8 unidades
(1) (2)
100 100
100 100 10
10
Una con líneas el número y el nombre que corresponden.
(1) 1 2 1 quinientos sesenta y nueve
(2) 3 4 7 trescientos cuarenta y siete
(3) 5 6 9 ciento veintiuno
Conteste las preguntas.
(3) ¿Cuántas unidades hay en 183?
(2) ¿Cuántas centenas hay en 947?
(1) ¿Cuántas decenas hay en 625?
Doscientos treinta y seis se
escribe 236 con números.
Porque hay 2 centenas,
3 decenas y 6 unidades.
centenas (C) decenas (D) unidades (U)
632
Se omite la lectura
424 581
968
2 decenas
9 centenas
3 unidades
(3/6)

32. Guía para maestros/as - Matemática 20
Grado 13
Leamos y escribamos números
• Leer y escribir los números de tres cifras (con 0) apli-
cando lo aprendido en la posición decimal de los nú-
meros de dos cifras.
Lección 2:
(4/6)
Objetivo:
Materiales: (M) azulejos, tarjetas numerales
(N) azulejos, tarjetas numerales
1. Captar el tema.
M: Hoy vamos a seguir pensando
cómo se escriben números de
tres cifras.
2. Contar las hojas de papel. [D1]
M: ¿Cuántas hojas de papel hay?
¿Cómo las vamos a contar?
RP: Centenas por centenas, de-
cenas por decenas y unidades
por unidades.
* Después del trabajo indepen-
diente, concluir que hay 3 cente-
nas, 0 decenas y 4 unidades.
3. Pensar en la forma de escribir
el número de tres cifras con 0
en las decenas.
M: ¿Cuál es la diferencia con el
caso de la clase anterior?
RP: En esta cantidad, no hay
decenas.
* Es muy importante que los
niños y las niñas analicen la
analogía o la diferencia de los
problemas comparando con
los anteriores para aplicarlo
en la resolución. Así se puede
desarrollar una parte del pen-
samiento matemático.
M: ¿Cómo se escribiría?
Que se den cuenta de que se
puede escribir el número 0 en
la posición vacía.
4. Escribir los números cuyas
decenas y/o unidades son 0.
[D2]
M: ¿Cómo se escriben estas can-
tidades con los números?
Que apliquen lo aprendido.
5. Practicar la lectura y la es-
critura de los números. [D3]
* Aquí se practica la tríada de los
números de 3 cifras de todos
los tipos.
* Explicar la instrucción del juego
(véase Notas).
6. Resolver los ejercicios 6 y 7 .
[Instrucciones del juego]
Se practica la tríada en pareja en el ambiente del juego.
Hay 6 tipos de práctica.
1. Una persona dice un número y otra lo representa con los azulejos o lo
escribe (puede representar con las tarjetas numerales).
2. Una persona coloca azulejos representando una cantidad y otra lo escribe con los
números (puede representar con las tarjetas numerales) o lo lee.
3. Una persona escribe un número (puede representar con las tarjetas numerales) y
otra lo representa con los azulejos o lo lee.
102
Ciento dos
9nueve
D1 Cuente y escriba cuántas hojas de papel hay.
La cantidad de las hojas de
papel es
y se escribe .
trescientos cuatro
304
Porque hay 3 centenas,
0 decenas y 4 unidades.
2 Cuente y escriba cuántos sorbetes hay.
6 Escriba con números cuántos hay y léalos.
7 Escriba el número que corresponda.
(1) Novecientos tres ( )
(2) Doscientos sesenta ( )
(3) Quinientos ( )
3 0 4
C D U
5 1 0
C D U
3 Juegue con los números.
100 100 100
C D U
4 0 0
(1)
(3) (4) (5)
(1) (2)
(2)
Se omite la lectura
506270
600 180409
(4/6)
500
260
903

33. Unidad 1 - Números hasta 99914
1. Comentar lo observado.
M: ¿Qué observan en el dibujo?
Que se den cuenta que las pelo-
tasrepresentanlacantidaddelas
centenas, decenas y unidades.
2. Contar la cantidad de pelotas
de cada posición. [E1]
M: ¿Cuántas centenas, cuántas de-
cenas y cuántas unidades hay?
3. Pensar qué número repre-
senta el ábaco. [E1]
M: ¿Qué número está formado
con 2 centenas, 4 decenas y
9 unidades?
RP: 200 y 40 y 9 son 249.
* Si dicen solamente “2 cente-
nas, 4 decenas, 9 unidades”,
puede ser que los niños y las
niñas sólo tengan conciencia
de los dígitos 2, 4 y 9, pero sin
acompañarlos de la dimensión
de la cantidad. Por lo tanto
es recomendable dirigir la
expresión como: “2 centenas,
4 decenas y 9 unidades. 200
y 40 y 9 son 249” para aclarar
la dimensión de cada dígito.
4. Componer el número de tres
cifras que contiene 0. [E2]
5. Practicar la composición. [E3]
* Indicar que practiquen la com-
posición en pareja preguntan-
do mutuamente, por ejemplo,
“Hay 4 decenas, 8 decenas y
1 unidad. ¿Cuánto es?” etc. Se
puede usar las tarjetas nume-
rales para escoger los 3 dígitos
en el ambiente de juego.
6. Resolver los ejercicios 8 y 9 .
Leamos y escribamos números
• Componer números de tres cifras mediante la forma-
ción de grupos con centenas, decenas y unidades.
Lección 2:
(5/6)
Objetivo:
Materiales: (M) tarjetas numerales
(N) tarjetas numerales
Se introduce esta clase con el dibujo del ábaco cuyas
pelotas son de diferentes colores según la posición para
que sea claro la diferencia de valores. No obstante, en
el ejercicio 8 se utilizan las pelotas del mismo color para que
los niños y las niñas capten bien que el valor posicional diferencia
el valor de los elementos en cada posición solamente dependiendo de
la posición, pero ningún otro aspecto. En caso de que los niños y las
niñas muestren la dificultad, se debe explicar.
10 diez
E1 ¿Qué número está representado en el ábaco?
2 Hay 6 centenas y 3 unidades. ¿Qué número se forma?
9 Escriba en las casillas los números que corresponden.
(1) Cuente cuántas centenas, decenas
y unidades hay.
(2) Escriba en el cuaderno el número
formado.
Hay 2 centenas, 4 decenas y 9 unidades.
200 y 40 y 9 son 249.
3 Practique en pareja preguntando mutuamente en la manera de 2.
600 y 3 se forma 603.
8 Escriba en el cuadro el número formado por las centenas, decenas y unidades
y en las líneas los números que corresponden.
(1)
(2)
(3)
(4)
(5)
¿Qué número se forma con 2 centenas, 8 decenas y 5 unidades?
¿Qué número se forma con 3 centenas, 2 decenas y 7 unidades?
¿Qué número se forma con 4 centenas, 1 decena y 4 unidades?
¿Qué número se forma con 7 centenas, y 3 decenas?
¿Qué número se forma con 9 centenas, y 1 unidad?
______ y ______
centenas
decenas
unidades
C D U
(2)
son
______ y ______
centenas
decenas
unidades
C D U
(3)
son
C D U
____ y ____ y ____
centenas
decenas
unidades
son
C D U
(1)
285
327
414
730
901
2
7
0
270
200 70
5
0
2
502
500 2
(5/6)
3
5
6
300
356
50 6

34. Guía para maestros/as - Matemática 20
Grado 15
Sería mejor tratar también el contenido de observar un
número desde el punto de vista que lleva el sentido de la
multiplicación, por ejemplo, el número 120 está formado
por 12 decenas (12 x 10), 400 está formado por 40 decenas
(40x10) etc. para que los niños y las niñas tengan variedades en la
observación de números. Se puede introducir si el tiempo y el nivel del
aprendizaje de los niños y las niñas lo permiten.
Leamos y escribamos números
• Descomponer los números de tres cifras mediante la for-
mación de grupos con centenas, decenas y unidades.
Lección 2:
(6/6)
Objetivo:
Materiales:
1. Captar el tema.
M: ¿Qué observan en el dibujo?
RP: El ábaco sin pelota.
M: Hoy vamos a ir colocando las pe-
lotas en cada posición del ábaco
de acuerdo con el número.
2. Dibujar las pelotas en el ába-
co de modo que represente
413. [F1]
M: ¿Cuántas pelotas hay que colocar
en cada posición? ¿Por qué?
Quecaptenlaformadedescom-
poner un número.
3. Descomponer 413. [F1]
M: ¿Cuántas centenas, cuántas
decenas y cuántas unidades
forman 413?
RP: 413 está formado por 4 cen-
tenas, 1 decena y 3 unidades,
o sea, 400 y 10 y 3.
4. Descomponer el número de
tres cifras que contiene 0.
[F2]
* Al principio se puede dejar
que exprese la posición vacía
con 0, por ejemplo, 7 cente-
nas, 0 decenas y 2 unidades,
así. Pero en la expresión con
números, inducir que omita la
cantidad de posición vacía,
por ejemplo, no como “700 y
0 y 2” sino “700 y 2”.
5. Practicar la descomposi-
ción. [F3]
* Indicar que practiquen la des-
composición en pareja pre-
guntando mutuamente, por
ejemplo, “¿Cuántas centenas,
cuántas decenas y cuántas
unidades forman 598?” etc. Se
puede usar las tarjetas nume-
rales para escoger los 3 dígitos
en el ambiente de juego.
6. Resolver los ejercicios 10 y 11.
(M) tarjetas numerales
(N) tarjetas numerales
____centenas
____decenas
____unidades
____centenas
____decenas
____unidades
____centena
____decenas
____unidades
11once
F1 ¿Cuántas centenas, cuántas decenas y cuántas unidades forman
el número 413?
(1)
(2)
Dibuje en el gráfico del ábaco las pelotas
que representen 413.
Escriba en el cuaderno la respuesta. C D U
413 está formado por 4 centenas, 1 decena y 3 unidades (400 y 10 y 3).
2 ¿Cuántas centenas, cuántas decenas y cuántas unidades forman el número 702?
3 2Practique en pareja preguntando mutuamente en la manera de .
10 Dibuje en el ábaco las pelotas que representan el número indicado y escriba en la
línea los números que corresponden.
C D U
(1) (2)
C D U C D U
(3)127 360 408
127 está formado por
(4)
(5)
(3)
(2)
(1)
180 está formado por ___ centena, ___ decenas y ___ unidades (____ y ___).
209 está formado por ___ centenas, ___ decenas y ___ unidades (____ y ___).
872 está formado por ___ centenas, ___ decenas y ___ unidades (____ y ___ y ___).
565 está formado por ___ centenas, ___ decenas y ___ unidades (____ y ___ y ___).
934 está formado por ___ centenas, ___ decenas y ___ unidades (____ y ___ y ___).
360 está formado por 408 está formado por
( y y )
11 Escriba en las líneas los números que corresponden.
702 está formado por 7 centenas, 0 decenas y 2 unidades (700 y 2).
( y )( y )
(6/6)
1
2
7
3
6
0
4
0
8
400 8300 607100 20
3 49 30 4900
6 55 60 5500
7 28 70 2800
8 01 80100
0 92 9200

35. Unidad 1 - Números hasta 99916
1. Recordar lo aprendido.
M: ¿Qué observan en el dibujo?
RP: La línea con las rayitas, los
números, etc.
* Explicar que este tipo de lí-
nea se llama recta numérica
y preguntar cómo están los
números cuando se van hacia
derecha y izquierda.
Que recuerden que cuando
se va hacia la derecha los nú-
meros son mayores y cuando
se va hacia la izquierda los
números son menores.
2. Leer la recta numérica. [A1]-
[A2]
Que capten, a través de con-
testar las preguntas, que para
leer la recta numérica hay que
averiguar primero qué dimen-
sión representa la distancia
entre cada graduación.
3. Ubicar el número 580 en la
recta numérica. [A3]
4. Ubicar los números que es
cierta cantidad más (menos)
que un número dado en la
recta numérica. [A4]-[A5]
* Tomar en cuenta la dificultad
de que en caso de las gra-
duaciones de 10 en 10, si un
número es 10 más (menos)
que otro, solamente se pasa
1 graduación hacia la derecha
(izquierda).
* Sería recomendable hacer otros
ejercicios con las graduaciones
de diferente dimensión.
5. Resolver el ejercicio 1 .
(1) y (2) Las graduaciones de
10 en 10
(3) y (4) Las graduaciones de
1 en 1
(5) Las graduaciones de 5 en 5
Ordenemos números
• Representar números en la recta numérica.
• Leer las graduaciones de la recta numérica y ubicar
en ella los números de tres cifras.
Lección 3:
(1/2)
Objetivo:
Materiales: (M) recta numérica
12 doce
Lección 3: Ordenemos números
A Observe y conteste.
¿Qué cantidad representa cada una de las rayitas?
Escriba en cada casilla el número correspondiente.
Indique con la flecha la posición del número 580.
(1) ¿Cuántas rayitas se debe contar hacia la derecha de 500?
(2) ¿Cuántas unidades hay más que 500?
¿Qué número es 10 más que 500? Indique con la flecha.
¿Qué número es 10 menos que 700? Indique con la flecha.
Este tipo
de línea se llama
recta numérica.
1 Escriba en la casilla los números que corresponden.
(1)
1
2
3
4
5
100 200 400 500 600 700 800 9000
100 200 400 500 600 700 800 9000
100 200 400300 500 6000
(2)
16014012011060 70
(3)
388 389 391 392 393 395 396 397 398 402
(5)
85 90 95 105 115 120 125 145
(4)
270 280 320310
10
8 rayitas
80 unidades
(1/2)
90
300
290 300
420 510 580 690 850
110
281 299 307
250 550380 480
80 90 100 130 150
390 394 399 400 401
100 110 130 135 140

36. Guía para maestros/as - Matemática 20
Grado 17
Ordenemos números
• Ordenar los números de tres cifras ascendente y des-
cendentemente.
Lección 3:
(2/2)
Objetivo:
Materiales: (M) recta numérica
1. Comentar lo observado. [B]
M: ¿Qué diferencia hay entre esta
recta numérica y la de la clase
anterior?
* Confirmar que ésta es de 1
en 1 y no aparece el número
0 porque solamente está pre-
sentando una parte.
2. Encontrar los números que
aumentan de 1 en 1. [B1]
M: ¿Dónde está el número 200
y cuál número es una unidad
mayor que él?
M: ¿Dondé está el número 199
y cuál número es una unidad
mayor que él?
* Se utiliza la recta numérica
como un medio de apoyo para
encontrar los números.
* Hacer otros ejercicios del mis-
mo tipo haciendo hincapié en
el rango que tiene el número
donde cambia el dígito de
la centena o la decena. Por
ejemplo, el número que es 1
mayor que 209, 399, etc.
3. Encontrar los números que
disminuyen de 1 en 1. [B1]
M: ¿Dónde está el número 201
y cuál número es una unidad
menor que él?
M: ¿Dónde está el número 200
y cuál número es una unidad
menor que él?
* Hacer otros ejercicios del mismo
tipo, por ejemplo, el número que
es 1 menor que 210, 400, etc.
4. Nombrar un rango de nú-
meros que contenga un
número donde aumenta
(disminuye) el dígito de la
centena o la decena. [B2]
* (1) y (2) son los casos que se
aumentan los números.
(3) y (4) son los casos que se
disminuyen los números.
* Hacer otros ejercicios del mis-
mo tipo.
5. Resolver los ejercicios del
2 al 4 .
Para los niños y las niñas es más difícil trabajar con los
números que disminuyen que con los que aumentan. Si
hay tiempo, es mejor practicar un poco más usando la recta
numérica, para que se familiaricen. También puede usar la tabla
de los números de 0 a 99 que fue usado en 1er grado para que piensen
en el orden de los dos dígitos de la derecha.
Se puede realizar la actividad 4 (ejercicios 1 y 2) después de la 2, de modo
que se divide el contenido en 2 partes que son de “ascendente” y “descen-
dente”, dependiendo la situación de los niños y las niñas.
13trece
B Observe.
1 Encuentre los números siguientes.
2 Nombre los números.
(1)
(2)
(3)
(4)
El número sucesor mayor que 200
El número sucesor mayor que 199
El número antecesor menor que 201
El número antecesor menor que 200
201
200
200
199
(1) (2)
(3) (4)
Desde 190 hasta 220 Desde 90 hasta 120
Desde 220 hasta 190 Desde 120 hasta 90
2 Escriba el número que está después.
3 Escriba el número que está antes.
4 Escriba en cada casilla el número que corresponde.
103 259 300 599 609 799
(1) (2) (3) (4) (5) (6)
224 310 101 400 890 600
(1) (2) (3) (4) (5) (6)
(1) 417 418 423 424
(2) 596 597 598 603
(3) 114 113 112 107
(4) 803 802 797 796
190 200 210 220
419 420 421 422
599 600 601 602
801 800 799 798
(2/2)
104
223 309 100 399 889 599
260 301 600 610 800
111 110 109 108

37. Unidad 1 - Números hasta 99918
Lección 4:
(1/5)
1. Comentar la situación del
dibujo. [A1]
Que confirmen que la niña tie-
ne más mentas que el niño.
2. Conocer los símbolos «>» y
«<».
M: La niña tiene más mentas.
¿Por qué se puede decir así?
* Informar que se puede ex-
presar «mayor» y «menor»
con los símbolos «>» y «<»
respectivamente.
3. Practicar la escritura de «>»
y «<». [A2]
* Es recomendable informarles
que el lado de mayor abertura
siempre indica hacia el núme-
ro mayor.
4. Comparar 38 y 52. [A3]
M: Vamos a comparar 38 y 52.
¿Cuál es mayor? ¿Por qué?
* Al representar la cantidad con
los materiales semiconcretos,
se espera que los niños y las
niñas puedan justificar visual-
mente que 52 es mayor. La
razón de justificar que 52 es
mayor es muy importante, ya
que esto debe hacerles pensar
en la forma de comparar los
números de dos cifras.
Que se den cuenta que no se
pueden comparar los dígitos
de diferente valor posicional
de 38 y 52, por ejemplo el 8
de 38 y el 5 de 52.
* Confirmar que en los números
de dos cifras, comparando
primero los dígitos de las de-
cenas se puede saber cuál es
mayor.
* Confirmar que 52 es mayor
que 38 y escribir las relaciones
con los símbolos, «52>38» y
«38<52».
Continúa en la siguiente página…
mayor que
menor que
1 (1)
(2)
(3)
¿Cuántas mentas tiene la niña?
¿Cuántas mentas tiene el niño?
¿Quién tiene más mentas?
A Observe y conteste.
La niña tiene 10 mentas y el niño tiene 5.
La niña tiene más mentas que el niño porque 10 es mayor que 5.
(El niño tiene menos mentas que la niña porque 5 es menor que 10.)
Uvas
CONFIT ES
Uvas Uvas
CO
NFIT ES
Uvas
Uvas
CO
NFIT ES
Uvas Uvas
CO
NFITES
Uvas Uvas
CONFITES
Uvas
Uvas
CONFIT ES
Uvas Uvas
CO
NFIT ES
Uvas
Uvas
CO
NFIT ES
Uvas Uvas
CO
NFIT ES
Uvas Uvas
CONFIT ES
Uvas
Naranja
CONF ITES
Naranja Naranja
C ON FITES
Naranja Naranja
C ON FITES
Naranja Naranja
CONF ITES
Naranja Naranja
C ON FITES
Naranja
10 es mayor que 5.
10 5>
Uvas
CONFIT ES
Uvas Uvas
CO
NFITES
Uvas
Uvas
CO
NFITES
Uvas Uvas
CO
NFITES
Uvas Uvas
CONFIT ES
Uvas
Uvas
CONFIT ES
Uvas Uvas
CO
NFIT ES
Uvas
Uvas
CO
NFIT ES
Uvas Uvas
CO
NFIT ES
Uvas Uvas
CONFITES
Uvas
Naranja
CONF ITES
Naranja Naranja
CON F ITES
Naranja Naranja
C ON FITES
Naranja Naranja
CONF ITES
Naranja Naranja
CON FITES
Naranja
5 es menor que 10.
5 10
2 Escriba los símbolos.
Este símbolo siempre abre la
boca hacia el número mayor.
3 Compare.
52 > 38.
52 tiene 5 decenas y 38 tiene sólo
3 decenas.
(1) ¿Cuál es mayor, 38 ó 52? ¿Por qué?
38
52 52 > 38, 38 < 52
catorce
Uva
s
C
ONFITES
Uva
s Uva
s
C
ONFITES
Uva
s
Uva
s
C
ONFITES
Uva
s Uva
s
C
ONFITES
Uva
s Uva
s
C
ONFITES
Uva
s
Uva
s
C
ONFITES
Uva
s Uva
s
C
ONFITES
Uva
s
Uva
s
C
ONFITES
Uva
s Uva
s
C
ONFITES
Uva
s Uva
s
C
ONFITES
Uva
s
Naranja
CONFITES
Naranja
Naranja
CONFITES
Naranja
Naranja
CONFITES
Naranja
Naranja
CONFITES
Naranja
Naranja
CONFITES
Naranja
14
Lección 4: Comparemos números
(1/5)
Comparemos números
• Conocer los símbolos «>» y «<» que expresan la re-
lación «mayor que» y «menor que» respectivamente,
y expresar estas relaciones utilizando los símbolos.
Objetivo:
Materiales: (M) azulejos (N) azulejos

38. Guía para maestros/as - Matemática 20
Grado 19
Comparemos númerosLección 4:
(1/5)
[Continuación]
… viene de la página anterior
5. Comparar 22 y 25.
M: Vamos a comparar 22 y 25.
¿En qué posición compara-
mos primero?
RP: Las decenas.
* Llamar la atención por tener
dígitos iguales en las dece-
nas.
M: ¿Cómo podemos compararlos
en este caso?
RP: Ahora vamos a comparar las
unidades.
* Confirmar que 25 es mayor
que 22 comparando los dígi-
tos de las unidades porque 5
es mayor que 2 y escribir las
relaciones con los símbolos,
«25>22» y «22<25».
Que capten que al comparar
dos números de dos cifras,
primero deben comparar los
dígitos de las decenas, y el
número mayor será el que
tenga el mayor dígito en las
decenas; pero si éstos son
iguales, deben comparar los
dígitos de las unidades y el
número mayor será el que
tengan el mayor dígito en las
unidades.
6. Resolver el ejercicio 1 .
* En caso de comparar 23 y
32 existe la posibilidad que
los niños y las niñas se con-
fundan al comparar tanto las
decenas como las unidades,
intercambiándolas al tomar
una decena de un número con
las unidades del otro por esta
razón el maestro o la maestra
debe hacerles ver que primero
se comparan las decenas y
después las unidades.
[Tipos de comparación entre dos números de dos
cifras]
A) Las decenas son iguales (22 y 25, 45 y 48, 71 y 79, etc.)
B) Las unidades son iguales (34 y 74, 18 y 38, 20 y 10, etc.)
C) Las decenas como las unidades son mayores (85 y 21, 17 y 59, 44 y 57, etc.)
D) Las decenas y unidades son mayores y menores (52 y 38, 57 y 84, 45 y 38).
(2) ¿Cuál es mayor, 22 ó 25? ¿Por qué?
Al comparar el tamaño de los números de dos cifras, primero se
comparan los dígitos de las decenas. Si son iguales, se comparan
los dígitos de las unidades.
25 > 22.
Ambos tienen 2 decenas pero
comparando las unidades, se
nota que 25 tiene 5 unidades
y 22 tiene sólo 2.
25 > 22, 22 < 25
1 Escriba en los cuadrados los símbolos (<,>,=) que corresponden.
quince
22
25
16 28
19 31
13 26
16 32
40 50
29 37
59 54
41 51
76 62
63 63
97 90
88 89
(2)
(5)
(8)
(11)
(14)
(17)
(20)
(23)
(26)
(29)
(32)
(35)
15 36
5 7
12 32
17 26
46 36
40 40
49 47
37 34
76 54
77 48
83 93
93 96
(1)
(4)
(7)
(10)
(13)
(16)
(19)
(22)
(25)
(28)
(31)
(34)
15 30
27 16
14 28
15 17
50 30
42 52
34 54
76 65
78 61
48 55
80 91
80 90
(3)
(6)
(9)
(12)
(15)
(18)
(21)
(24)
(27)
(30)
(33)
(36)
15

39. Unidad 1 - Números hasta 99920
1. Captar la situación del pro-
blema. [B]
M: ¿Qué tenemos que hacer?
RP: Comparar el número de estu-
diantes de la escuela de María
con los de las otras escuelas.
2. Comparar los números de
tres cifras.
M: ¿Qué usamos para represen-
tar cuál es mayor o menor?
* Recordar el sentido y la escri-
tura de los signos de “mayor
que” y “menor que”.
M: ¿Cómo sería mejor para com-
parar? Vamos a compararlos
y escribir en el cuaderno la
respuesta usando los signos.
* Confirmarquecomparenlostres
casos presentados en el LE.
* Se puede usar los azulejos
como la ayuda para pensar.
Que se den cuenta que:
1: 482 < 513 porque compa-
rando las centenas, 513 tiene
más azulejos que 482
2: 482 > 467 porque 482 tiene
8 decenas y 467 tiene sólo 6
3: 482 < 489 porque el dígito
de las unidades que tiene 482
es menor que 489.
3. Expresar las respuestas.
* Pedir siempre la razón de los
resultados obtenidos.
4. Concluir la forma de com-
parar los números.
* Aprovechando las expresiones
de los niños y las niñas, con-
cluir que se puede comparar
los números empezando de los
dígitos de la posición superior.
5. Resolver los ejercicios del
2 al 4 .
Continúa en la siguiente página…
[Otro ejemplo del juego]
<Hagamos el grupo según el número>
* Sería mejor realizarlo en un lugar amplio, por ejemplo en la cancha.
1. Escribir cualquier número que le guste en un papel.
2. Guardarlo en su bolsillo y caminar libremente cantando juntos.
3. Al terminar la canción el maestro o la maestra da palmadas. Se puede usar
algún instrumento o decir el número en voz fuerte en vez de las palmadas.
Continúa en la siguiente página…
16 dieciséis
B En la escuela de María hay 482 estudiantes.
En la de José hay 513, la de Ana 467 y en la de Carlos 489.
Compare el número de estudiantes de la escuela de María con la de los otros.
482 < 513 482 > 467 482 < 489
Se puede comparar los números empezando desde los dígitos de la
posición superior.
2 Compare y escriba el símbolo < ó > en la línea.
482
513
María
José
482
467
María
Ana
482
489
María
Carlos
¿De cuál posición de dígito
empiezo a comparar?
4 8 2
5 1 3 4 6 7
(5) (6) (7)
(8) (9) (10)
312 ____ 315 624 ____ 426 105 ____ 94
801 ____ 799 9 ____ 205 601 ____ 610
(1) (2)
(3) (4)
4 8 2 4 8 2
4 8 9
< > >
> < <
> >
< <
(2/5)
Comparemos númerosLección 4:
(2/5)
Objetivo:
Materiales:
• Comparar y ordenar números usando la recta numé-
rica y/o el valor posicional.
• Determinar la dimensión de los números de tres ci-
fras y expresarlo utilizando los signos de desigualdad
y ordenar los números según su dimensión.
(M) azulejos (N) azulejos, tarjetas numerales

40. Guía para maestros/as - Matemática 20
Grado 21
Comparemos númerosLección 4:
(2/5)
[Continuación]
… viene de la página anterior
3
* Son más difíciles los ejercicios
de ordenar los números que
los de comparar la dimensión
de dos números porque se
necesita mucha memoria para
resolverlo. Si hay niños y niñas
que no pueden ordenarlos
bien, sería mejor permitirles
usar papeles de modo que
escriban cada número en cada
papel y los ordenen.
4
* Hay que confirmar que hay
varias respuestas. Se puede
encontrar las respuestas pro-
bando los números de 0 a 9
uno por uno. Preguntar cómo
resolvieron y si hay niños y ni-
ñas que descubrieron la forma
más fácil de encontrar las res-
puestas, felicitarlos mucho y
experimentarlo todos juntos.
[Nos divertimos]
No hay distribución de horas.
Son los ejercicios de la com-
paración y sucesión de los
números (véase Notas).
* En el juego de < ¿Quién saca el
mayor?>, se puede cambiar la
regla libremente, por ejemplo:
- En vez de abrir las tarjetas
desde las unidades, abrirlas
desde las centenas.
- En vez de sacar las tarjetas
sin verlas, dejar que las vean
y formen un número para que
sea mayor.
* En el juego de <El tercero
gana>, se puede cambiar la
regla libremente, por ejemplo:
- En vez de ordenar de mayor
a menor, ordenar de menor a
mayor.
- En vez de el tercero gana, el
que escribió el cuarto número
gana.
… viene de la página anterior
4. Formar grupos que sean de la cantidad correspondiente al nú-
mero de palmadas, por ejemplo, si son 5 palmadas, forman grupos de
5 personas.
5. Sacar el papel con el número escrito y mostrárselo a las personas del grupo y
hacer una fila de menor a mayor según el número que tienen.
6. El grupo que se ordenó primero gana.
* Puede repetir este juego cantando y caminando libremente otra vez y forman-
do nuevos grupos según la cantidad de las palmadas.
3 Ordene los siguientes números según las indicaciones.
(1) 523, 356, 120, 16, 201, 400 (de mayor a menor)
(2) 62, 126, 506, 231, 487, 704 (de a )menor mayor
4 Los siguientes ejercicios son comparaciones de números de 3 cifras.
(1) (2)
(3) (4)
2 6 5 2 4< 7 3 6 7 4
3 5 7 3< 7 5 4 8 9<
Nos divertimos
Vamos a jugar comparando números.
¿Quién saca el mayor?
1:
2:
3:
4:
5:
Formar parejas.
Cada uno toma tarjetas
numerales mezcladas.
Cada uno saca 3 tarjetas
sin ver los números y las
coloca con la cara hacia abajo.
Abrirlas desde las unidades.
El que formó el número
mayor gana.
El tercero gana
1:
2:
3:
4:
Formar grupos de 5 ó 6 personas.
Cada uno forma con las tarjetas
numerales (ó puede escribir en el
cuaderno) un número que le guste de
hasta 3 cifras sin que los demás vean.
Mostrar mutuamente el número y
ordenarlos de mayor a menor todos
juntos.
Gana quien formó el tercer número.
2
67
375
18
¡Gané!
1
17diecisiete
Escriba en la línea qué número estaba escrito en la parte rota.
(Puede haber varias respuestas).
523, 400, 356, 201, 120, 16
62, 126, 231, 487, 506, 704
7, 8, 9 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
1, 2, 3, 46, 7, 8, 9

41. Unidad 1 - Números hasta 99922
Comparemos números
• Encontrar los números naturales que están entre dos
números dados.
Lección 4:
(3/5)
Objetivo:
Materiales:
1. Captar la situación del pro-
blema. [C1]
M: ¿Qué hay que encontrar?
Que se den cuenta que hay
que encontrar el número que
está entre 30 y 32.
* Escribir en la pizarra “30 < <
32” para aclarar la situación.
2. Determinar el número que
está entre 30 y 32.
M: ¿Qué número está entre 30 y
32? ¿Por qué?
RP: 31. Porque es mayor que 30
y menor que 32.
* Escribir en la pizarra rela-
cionando 3 números con los
signos de desigualdad y ex-
plicarlo.
* Preguntar si 35 es apropiado
para la respuesta. Confirmar
que es correcta la relación 30
< 35 pero no es correcta la re-
lación 35 < 32. Por lo tanto, 35
no puede estar entre 30 y 32.
3. Determinar si 330 está entre
280 y 410. [C2]
M: Vamos a pensar si 330 está
entre 280 y 410 o no.
* Insinuar la solución escribien-
do en la pizarra “280 < <
410”.
* Designar algunos niños y
niñas para que expliquen las
opiniones.
* Confirmar que sí 330 está en-
tre 280 y 410 razonando sí es
lógico 280 < 330 y 330 < 410.
4. Resolver 5 y 6 .
* Véase Notas.
1. Captar el tema.
M: ¿Cuántas habichuelas agarré,
aproximadamente?
Que capten que aproximarán
la cantidad.
Continúa en la siguiente página…
En la resolución del ejercicio 5 , se debe aprovechar
las respuestas de los niños y las niñas que escribie-
ron no sólo los números continuos (por ejemplo, 52, 53,
54,....) sino que también los separados (por ejemplo, 52, 55, 58,
60,...) para cultivar un mejor entendimiento sobre los números que es-
tán entre dos números dados. En este grado solo nos referimos a nú-
meros naturales.
(M) recta numérica
[Hasta aquí 3/5]
[Desde aquí 4/5~5/5]
18 dieciocho
C1 La mamá de Pedro tiene más de 30 años y menos de 32 años.
¿Cuántos años tiene la mamá de Pedro?
2 Piense si 330 está entre 280 y 410.
5 Escriba en la línea todos los números que están entre los dos números dados.
6 Escriba en la línea 5 números que están entre los dos números dados.
(1) 45 y 54 _______________________________________________________
(2) 113 y 119 _______________________________________________________
(3) 417 y 421 _______________________________________________________
(4) 398 y 403 _______________________________________________________
(1) 51 y 64 _______________________________________________________
(2) 442 y 465 _______________________________________________________
(3) 190 y 203 _______________________________________________________
(4) 674 y 833 _______________________________________________________
D1 ¿Cuál número queda más cerca de 32; 30 ó 40?
30 queda más cerca a 32 que 40.
30 es la decena próxima a 32.
30 < 31 31 < 32
30 < 31 < 32
y
31 está entre 30 y 32. Ella tiene 31 años.
29 30 31 32 33 3428
280 330 410
330 está entre 280 y 410.
280 290 330 340 420270 310 320 360 370350 380 400 410390300
30
32
40
(3/5)
(4/5 ~ 5/5)
399, 400, 401, 402
418, 419, 420
114, 115, 116, 117, 118
46, 47, 48, 49, 50, 51, 52, 53
Se omite la solución (puede haber varias respuestas)

42. Guía para maestros/as - Matemática 20
Grado 23
… viene de la página anterior
2. Encontrar cuál es más cerca a
32, 30 ó 40. [D1]
M: Las habichuelas son 32. ¿Aproxi-
madamente cuántas decenas de
habichuelas tengo? ¿Por qué?
Que capten que 32 es casi 3 de-
cenas porque 32 es más cerca a
30 que 40.
* Explicar el término “la decena próxi-
ma” (el múltiplo de 1 decena que
está más cerca al número dado).
3. Encontrar la decena próxima
de 37. [D2]
M: Si tengo 37 habichuelas, ¿cuál es
la decena próxima, 30 ó 40? ¿Por
qué?
4. Confirmar las aproximaciones
de las decenas próximas a los
números de 30 a 40.
* Concluir que tomando 35 como el
criterio, se separan en dos grupos
de números que toman 30 como la
decena próxima y otros que toman
40 (y 35 pertenece a este grupo
superior).
5. Resolver el ejercicio 7 .
Comparemos números
• Conocer el concepto de la decena próxima y de la
centena próxima y encontrarlas.
Lección 4:
(4/5~5/5)
Objetivo:
Materiales: (M) habichuelas, recta numérica
[Hasta aquí 4/5]
[Desde aquí 5/5]
2 ¿Cuál es la decena próxima a 37, 30 ó 40?
40 queda más cerca a 37 que 30.
La decena próxima a 37 es 40.
7 Encuentre la decena próxima para cada número siguiente.
E1 ¿Cuál número queda más cerca de 215, 200 ó 300?
19diecinueve
200 queda más cerca a 215 que 300.
200 es la centena próxima a 215.
2 ¿Cuál es la centena próxima a 260, 200 ó 300?
300 queda más cerca a 260 que 200. La centena próxima a 260 es 300.
8 Encuentre la centena próxima para cada número siguiente.
30 40
37
(1) 23 (2) 25 (3) 28 (4) 52 (5) 55
(6) 56 (7) 80 (8) 85 (9) 89 (10) 40
190 200 210 220 230 240 250 270 280 290 300 310260
260
(1) 120 (2) 149 (3) 150 (4) 247 (5) 251
(6) 399 (7) 400 (8) 473 (9) 601 (10) 750
28 29 30 31 32 33 34
decena próxima
35 36 37 38 39 40 41
250 está en medio de 200 y 300. En caso de
250 se toma el 300 como la centena próxima.
215
190 200 210 220 230 240 250 270 280 290 300 310260
190 200 210 220 230 240 250 270 280 290 300 310260
centena próxima
35 está en medio de 30 y 40. En caso de 35
se toma el 40 como la decena próxima.
20 30 30 50 60
60 80 90 90 40
100 100 200 200 300
400 400 500 600 800
* Continuar con las centenas próxi-
mas utilizando el mismo proceso
de la clase anterior.
1. Captar la diferencia de la recta
numérica.
2. Encontrar cuál es más cerca a
215, 200 ó 300. [E1]
M: ¿Aproximadamente cuántas cen-
tenas son el número 215? ¿Por
qué?
* Concluir y explicar el término “la
centena próxima” (el múltiplo de
1 centena que está más cerca al
número dado).
3. Encontrar la centena próxima
de 260. [E2]
4. Confirmar las aproximaciones
de las centenas próximas a los
números de 200 a 300.
5. Resolver el ejercicio 8 .

43. Unidad 2 - Números ordinales24
1
• Usan números ordinales para describir situaciones de su vida cotidiana.
Números ordinales
Expectativas de logro
(2 horas)Unidad
22
Números hasta 999
• Concepto de «centena».
• Leer, escribir y construir
el significado de los
números hasta 999.
• Composición y descom-
posición de números de
tres dígitos.
• Representar números
de tres dígitos en la
recta numérica.
• Orden de números de
tres dígitos.
• Comparar números de
tres dígitos.
Números hasta 9,999
• Concepto de «unidad
de mil».
• Leer, escribir y construir
el significado de los
números hasta 9,999.
• Composición y descom-
posición de números de
cuatro dígitos.
• Representar números
de cuatro dígitos en la
recta numérica.
• Orden de números de
cuatro dígitos.
• Comparar números de
cuatro dígitos.
Números hasta 1,000,000
• Concepto de «decena
de mil», «centena de
mil».
• Leer, escribir y construir
el significado de los nú-
meros hasta 1,000,000.
• Composición y descom-
posición de números
hasta 1,000,000.
• Representar números
hasta 1,000,000 en la
recta numérica.
• Orden de números
hasta 1,000,000.
• Comparar números
hasta 1,000,000.
• Redondeo de números.
• Numeración romana.
Relación de objetos y
elementos
Grupos de objetos y
elementos
Relación y desarrollo2
Números hasta 9
• Leer, escribir y construir
el significado de los
números del 1 al 9.
• Concepto del cero (0).
• Orden de números del
cero al 9.
• Composición y descom-
posición de números
entre 1 y 9.
Números ordinales
• Números ordinales
hasta 20º.
Números hasta 19
• Concepto de «unidad» y
«decena».
• Composición y descom-
posición del número 10.
• Leer, escribir y construir
el significado de los
números hasta 19.
• Representar números
hasta 19 en la recta
numérica.
Números ordinales
• Números ordinales
hasta 10º.
• Orden y posición de
números.
• Concepto de número
cardinal y ordinal.

44. Guía para maestros/as - Matemáticas 2o
grado 25
Puntos de lección
• Lección 1: Conozcamos sobre los
números ordinales
En esta unidad se aprende el nombre y los
símbolos de los números ordinales hasta 20º
(vigésimo). Es bastante difícil que en una o
dos clases los niños y las niñas logren memo-
rizar los números ordinales, por eso es muy
importante que el maestro o la maestra pon-
ga mucha atención en su enseñanza y para
alcanzar el aprendizaje se sugiere pegar los
números en la pared, utilizarlos en diferentes
ocasiones como en el juego, al hacer la fila, al
terminar la tarea, etc., y en los grados supe-
riores ampliar su conocimiento.
4
3 Plan de estudio (2 horas)
1/2~2/21. Conozcamos sobre los
números ordinales (2 horas)
• Los números ordinales del 11º hasta 20º
Los números ordinales del 21o
hasta el 100o
son:
21
O
22
O
23
O
24
O
25
O
26
O
27
O
28
O
29
O
Vigésimo Primero
Vigésimo Segundo
Vigésimo Tercero
Vigésimo Cuarto
Vigésimo Quinto
Vigésimo Sexto
Vigésimo Séptimo
Vigésimo Octavo
Vigésimo Noveno
30
O
31
O
32
O
33
O
34
O
35
O
36
O
37
O
38
O
39
O
Trigésimo
Trigésimo Primero
Trigésimo Segundo
Trigésimo Tercero
Trigésimo Cuarto
Trigésimo Quinto
Trigésimo Sexto
Trigésimo Séptimo
Trigésimo Octavo
Trigésimo Noveno
40
O
41
O
42
O
43
O
44
O
45
O
46
O
47
O
48
O
49
O
Cuadragésimo
Cuadragésimo Primero
Cuadragésimo Segundo
Cuadragésimo Tercero
Cuadragésimo Cuarto
Cuadragésimo Quinto
Cuadragésimo Sexto
Cuadragésimo Séptimo
Cuadragésimo Octavo
Cuadragésimo Noveno
50
O
80
O
Quincuagésimo
Octogésimo
60
O
90
O
Sexagésimo
Nonagésimo
70
O
100
O
Septuagésimo
Centésimo
Columnas
Números hasta 99
• Leer, escribir y construir
el significado de los
números hasta 99.
• Orden de números
hasta 99.
• Contar en grupo de 2, 5
y 10.

45. Unidad 2 - Números ordinales26
Conozcamos sobre los números
ordinales
Lección 1:
(1/2~2/2)
• Expresar el orden de los números ordinales desde 1º
a 20º.
Objetivo:
Materiales:
1. Captar el tema . [A]
M: ¿Qué están haciendo las per-
sonas?
RP: Una competencia de carrera.
2. Comentar el orden de la com-
petencia con los números or-
dinales.
M: Ana está en el décimo lugar.
¿Quiénes siguen?
* Hacer que escriban el nombre
de las personas en la pizarra,
según el orden de llegada, si
es posible.
* Indicar que escriban los nú-
meros ordinales bajo cada
nombre según corresponda,
para confirmar el orden.
3. Leer en orden los números
ordinales de décimo a vigé-
simo. [A1]
4. Expresar el orden, aclarar la
posición del punto de refe-
rencia y la dirección del or-
denamiento.
M: Desde adelante, ¿en qué posi-
ción se encuentra Delmy?
* Indicar que utilicen los núme-
ros ordinales (décimo a vigé-
simo) señalando las posicio-
nes en el LE.
M: Desde atrás, ¿en qué posi-
ción se encuentra Delmy?
* Informar que se cambió el
punto de referencia (desde el
final hacia el frente).
* Pedir a los niños y a las niñas
que identifiquen en qué posi-
ción están las otras personas.
Continúa en la siguiente página… [Sobreponiendo las manos contando hasta vigésimo]
Un niño o niña coloca la mano y dice primero, después
otro niño o niña coloca la mano y dice segundo, después
coloca la otra mano y dice tercero, luego cuarto hasta llegar a
vigésimo; quien coloque la mano en el vigésimo lugar es el ganador;
el maestro o la maestra puede decidir el premio.
(Primero dos niños o niñas, después tres, etc.) 1º 2º
Lección 1: Conozcamos sobre los números ordinales
A Observe y comente.
Ana
Luis
Soledad
Delmy
Roberto
Nely
Moisés
Beatriz
Gloria
Julio
Owen
1 Aprenda los números ordinales hasta 20O
.
Decimocuarto
Vigésimo
Décimo
Décimoprimero
Décimosegundo
Decimotercero
Decimoquinto
Decimosexto
Decimoséptimo
Decimoctavo
Decimonoveno
20
o
19
o
18
o
17
o
16
o
15
o
14
o
13
o
12
o
11
o
10
o
10o
20 veinte
Unidad 2 Números ordinales
Leo y escribo los números ordinales que faltan.
Recordemos
1
o
, 2
o
, , 4
o
, 5
o
, 6
o
, , 8
o
, y .
(1/2~2/2)
3
o
7
o
9
o
5 Desarrollo de
clases

46. Guía para maestros/as - Matemáticas 2o
grado 27
Lección 1:
(1/2~2/2)
Conozcamos sobre los números
ordinales
… viene de la página anterior
5. Jugar usando los números
ordinales.
* En parejas que realicen al-
gunos juegos o actividades
usando los números ordina-
les (veáse Notas).
* Orientar para que inventen otros
juegos y que los practiquen.
6. Afianzar el conocimiento de los
números ordinales de 1º a 20º.
M: Desde el frente, ¿qué animal
está en el décimoprimer lugar?
M: Desde atrás, ¿qué animal está
en el décimosegundo lugar?
* Preguntar por otros lugares.
M: Desde el frente, ¿en qué po-
sición va el elefante?
M: Desde atrás, ¿en qué posi-
ción va el sapo?
* Preguntar por otros animales.
* Indicar que formen equipos o
parejas y que entre ellos hagan
preguntas como las anteriores.
7. Confirmar la diferencia en-
tre los números ordinales y
los números cardinales.
M: Mencionen el animal que está
en el décimoprimer lugar,
desde el frente.
RP: El sapo.
M: Mencionen once animales
desde el frente.
* Preguntar por otros lugares y
cantidades de animales cam-
biando la dirección.
Que se den cuenta de la di-
ferencia que existe entre un
número ordinal y un número
cardinal explicándolo con sus
propias palabras.
8. Resolver los ejercicios 1 y 2 .
[Continuación]
[Hasta aquí 1/2]
[Desde aquí 2/2]
Escribe con el número
ordinal el orden en que
va cada animal en mi tren.
1 Escriba y lea los números ordinales.
21veintiuno
2 Uno con la línea.
Décimoprimero
Decimoctavo
Vigésimo
Décimosegundo
Decimocuarto
Decimoséptimo
18
O
11
O
14O
17
O
20O
12O
2
O 3
O
4
O 5
O
6O7O8O
9O
11O
12O
13O14O
15O 16O
17
O
18O
19O

47. Unidad 3 - Suma28
3
• Aplicando el concepto de adición calculan sumas donde los sumandos son menores que 100, sin
reagrupar y reagrupando
• Resuelven problemas de la vida cotidiana que implican la adición cuyos sumandos sean menores
que 100, sin reagrupar y reagrupando.
Suma
Expectativas de logro
(18 horas)Unidad
1
3
Números hasta 999 Números hasta 9,999 Números hasta 1,000,000Números hasta 9
Relación y desarrollo2
Suma (1)
Adición cuyo total sea
menor o igual que 9
• Sentido de la suma
(“agrupación” y “agrega�
ción” o “suplemento”).
• Operación de la suma
cuyo total sea menor o
igual que 9.
• Planteamiento de la
operación.
• Procedimiento de ope�
ración.
• Operación de la suma
con 0.
Suma
Adición cuyos sumandos
sean menor que 100
• D0 +D0.
• D0 + U, U + D0.
• Procedimiento de la
adición vertical.
• DU + DU, sin reagrupar.
• DU + U, U + DU, sin
reagrupar.
• DU + DU, reagrupando
• DU + U, U + DU, re�
agrupando.
• DU + DU = CDU,
reagrupando una vez y
dos veces.
Adición
Adición con sumandos
menores que 1,000
• CDU + CDU, sin reagru�
par.
• CDU + DU, U, sin re�
agrupar.
• CDU + CDU, reagru�
pando una vez.
• CDU + DU, U, reagru�
pando una vez.
• CDU + CDU, DU, U,
reagrupando dos y tres
veces.
Adición y sustracción
Adición y sustracción con
números menor o igual
que 1,000,000
Aproximación de adición y
sustracción
Números hasta 19
Suma y resta combinada
• Suma con tres suman�
dos.
• Resta con tres sus�
traendos.
• Suma y resta combina�
das.
Operaciones combinadas
• Orden de cálculo.
• Uso de paréntesis.
• Propiedad asociativa de
la adición.
• Propiedad asociativa de
la multiplicación.Suma (2)
Adición cuyo total sea
menor que 18
• U + U reagrupando.
• Suma con tres suman�
dos.
Números hasta 99

48. Guía para maestros/as- Matemática 20
Grado 29
1/3 • Operación del tipo D0+D0
3 Plan de estudio (18 horas)
1. Sumemos (3 horas)
2. Sigamos sumando (4 horas)
2/3 • Operación del tipo D0+U
3/3 • Operación del tipo U+D0
1/4 • Operación del tipo DU+DU, sin reagrupar
2/4 • Operación del tipo D0+DU y DU+D0, sin reagrupar
3/4 • Operación del tipo DU+U, sin reagrupar
4/4 • Operación del tipo U+DU, sin reagrupar
1/1 • Aplicación y dominio de la lección 2 Ejercicios (1) (1 hora)
3. Sumemos reagrupando
(7 horas)
1/7 • Operación del tipo DU+DU, reagrupando
2/7~3/7 • Operación del tipo DU+DU=D0, reagrupando
4/7 • Operación del tipo DU+U, reagrupando
5/7 • Operación del tipo U+DU, reagrupando
6/7 • Operación del tipo DU+DU=CDU, reagrupando una vez
7/7 • Operación del tipo DU+DU=CDU, reagrupando dos veces
1/1 • Aplicación y dominio de la lección 3 Ejercicios (2) (1 hora)
1/2~2/2 • Aplicación y dominio de la unidad 3 Ejercicios (3) (2 horas)

49. Unidad 3 - Suma30
Puntos de lección
• Lección 1: Sumemos
Al iniciar esta unidad se toca el contenido de
D0+D0, D0+U y U+D0 (los casos fáciles para
el cálculo mental) en forma horizontal para
que los niños y las niñas desarrollen el cálculo
pensando la composición de los números. Se
pueden manipular los materiales semiconcre�
tos como apoyo para aclarar la construcción
de los números.
• Lección 2: Sigamos sumando
Es muy importante que los niños y las niñas
comprendan que para calcular en la forma
vertical se hace sumando los números que
se encuentran en la misma posición (unidad
con unidad y decena con decena) y que se
deben sumar primero las unidades. Además
debemos tener presente la importancia del
planteamiento de la operación con que se tra�
duce una situación o problema al lenguaje
matemático. Por otro lado, es importante que
los niños y niñas entiendan que el cálculo ver�
tical no es la operación en sí, sino una forma
auxiliar para encontrar el resultado.
• Lección 3: Sumemos reagrupando
El principal objetivo de esta unidad es el sig�
nificado y el procedimiento de la suma reagru�
pando. Es muy importante que los niños y las
niñas observen y manipulen directamente los
materiales semiconcretos para profundizar
la comprensión de dicho procedimiento. Hay
que mostrarles y hacerles entender bien por
qué al obtener 10 unidades se debe convertir
en una decena y llevarla a su lugar correspon�
diente. Para esto se debe repasar el valor de
posición.
Después que comprendan bien el significado
y el procedimiento de la suma reagrupando
se deben realizar muchos ejercicios para que
lo dominen bien.
4

50. Guía para maestros/as- Matemática 20
Grado 31
Tipos de suma
En la enseñanza de la suma DU+DU en la forma vertical se debe hacer sistemáticamente tomando
en cuenta la clasificación de los ejercicios, la cual se hace por el orden de dificultad: sin reagrupar y
reagrupando, no contiene “0” y contiene “0”.
Tomando en cuenta esta condición el maestro o la maestra puede inventar ejercicios de acuerdo al
grado de dificultad tal como se presenta a continuación.
[Clasificación de los ejercicios]
Cálculo horizontal (mental)
1) D0 + D0 (30 + 20) 2) D0 + U (40 + 6) 3) U + D0 (5 + 60)
Utilizando cálculo vertical (sin reagrupar)
1) DU + DU (31 + 21) 2) DU + D0 (31 + 20) 3) D0 + DU (30 + 21)
4) DU + U (31 + 2) 5) U + DU (3 + 21)
Utilizando cálculo vertical (reagrupando)
1) DU+DU = DU (18+24) 2) DU+DU = D0 (11+29) 3) DU+U = DU (56+5)
4) U+DU = DU (6+35) 5) DU + U = D0 (57 + 3) 6) U + DU = D0 (2 + 48)
7) DU + DU = CDU (74 + 58)
Los ejercicios clasificados se pueden aplicar en las clases para que los niños y las niñas dominen el
contenido. Además pueden usarlos en un examen para evaluar el nivel de comprensión de cada uno y
auto reflexionar sobre la forma de enseñanza. Luego, dependiendo del resultado el maestro o la maes�
tra puede organizar la clase de reforzamiento.
Unidad
Decena
Centena
D
+
U
Columnas
1
Los azulejos
Son materiales didácticos semiconcretos que se sugieren en esta Guía para la representación del
mecanismo del sistema posicional decimal sin perder la percepción de la cantidad, es decir, que man�
tienen la dimensión de la cantidad en su tamaño. Por lo tanto, son útiles en la orientación del cálculo
vertical, principalmente con los números de dos cifras. Los números mayores que mil no es recomen�
dable representarlos con los azulejos, porque es difícil de imaginar la cantidad en la mente. Además, el
propósito de usar los azulejos es relacionar el número con la cantidad real. Cuando se enseña la suma
con los números grandes, es probable que los niños y las niñas ya entiendan bien ese concepto y estos
materiales no sean necesarios. Al dibujar los azulejos es recomendable considerar la proporcionalidad
para que los niños y las niñas no se confundan y capten el concepto de cantidad claramente como lo
muestra la gráfica.
2

51. Unidad 3 - Suma32
SumemosLección 1:
(1/3)
• Realizar los cálculos del tipo D0 + D0 en forma horizontal.
(M) azulejos
(N) azulejos
Objetivo:
Materiales:
5 Desarrollo de
clases
1. Comentar la situación del
problema. [A]
* Orientar para que piensen con
cuál operación se puede en�
contrar el resultado.
2. Escribir el planteamiento
de la operación. [A1]
M: ¿Cómo será el planteamiento
de la operación? Escríbanlo
en sus cuadernos.
* No es necesario resolver en
este momento.
3. Encontrar la manera de cal-
cular. [A2]
* Indicar que utilicen los azule�
jos para resolver.
M: ¿Cómo hicieron?
RP: Representé con los azulejos
dos grupos de 10 que es la
cantidad de flores que tenía
María y otro grupo de 10 que
son las flores que su mamá
le regaló, entonces sumé 2
grupos más 1 grupo de 10 es
igual a 30.
Que se den cuenta que con�
virtiendo a las decenas se
puede encontrar la respuesta
fácilmente.
4. Confirmar la manera de cal-
cular “20 + 10”.
* Indicar que observen el LE y
analizar el proceso.
M: ¿Por qué el resultado es trein�
ta?
* Si surge en los niños y las niñas
la idea de sumar sólo los núme�
ros de las decenas y agregar
0 para encontrar el resultado,
hay que felicitarlos y se puede
concluir de esta forma.
5. Resolver el ejercicio 1 .
Para afianzar el contenido del problema principal se
puede realizar otros ejemplos del mismo tipo antes de
resolver los ejercicios del LE.
Lección 1: Sumemos
Unidad 3
A María tiene 20 flores y su mamá le regala 10 flores más.
¿Cuántas flores tiene María ahora?
22 veintidós
Suma
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
20 + 10
Planteamiento de la operación: 20 + 10 = ___
Respuesta: flores
1 Calcule las siguientes sumas.
(1) 10 + 20 = ___ (2) 30 + 10 = ___ (3) 50 + 40 = ___
(4) 20 + 50 = ___ (5) 30 + 40 = ___ (6) 20 + 60 = ___
(7) 40 + 40 = ___ (8) 70 + 10 = ___ (9) 20 + 20 = ___
(10) 80 + 10 = ___ (11) 60 + 30 = ___ (12) 30 + 30 = ___
D U
2 0
D U
1 0
D U
3 0+ =
+
tiene 20 flores le regala 10 flores más
María Mamá
30
30
30 40 90
70 70 80
80 80 40
90 90 60
(1/3)

52. Guía para maestros/as- Matemática 20
Grado 33
Lección 1:
(2/3)
Objetivo:
Materiales:
Sumemos
• Realizar los cálculos del tipo D0 + U en forma
horizontal.
(M) azulejos
(N) azulejos
1. Comentar la situación del
problema. [B]
* Orientar para que piensen con
cuál operación se puede en�
contrar el resultado.
2. Escribir el planteamiento
de la operación. [B1]
M: ¿Cómo será el planteamiento
de la operación? Escríbanlo
en sus cuadernos.
Que se den cuenta de la dife�
rencia que existe entre el tipo
anterior y éste (uno de los su�
mandos no tiene decena).
3. Encontrar la manera de cal-
cular. [B2]
* Indicar que utilicen los azule�
jos para resolver.
M: ¿Cómo hicieron?
RP: Representé con los azulejos
dos grupos de 10, que es la
cantidad de mangos que te�
nía José y otro grupo de 5,
que son los mangos que com�
pró después. Entonces tengo
2 grupos de 10 y 5 de 1, los
junté y me dio 25 mangos.
* Hacer la demostración en la
pizarra utilizando azulejos.
4. Confirmar la manera de cal-
cular “20 + 5”.
M: ¿Por qué el resultado es vein�
ticinco? ¿Por qué lo escribi�
mos así?
* Concluir que en este caso para
encontrar el resultado no se
suma el número que está en
la posición de la decena con el
número que está en la posición
de las unidades. Es necesario
colocar cada uno en su lugar
de posición correspondiente.
5. Resolver el ejercicio 2 .
Hay muchos niños y niñas que pueden decir que 20 + 5 = 25,
pero hay errores en la escritura (“20 + 5 = 205”) o se confun�
den en la casilla de la tabla de valores al colocar el número que
representa la unidad o la decena, se debe poner atención y corregir
si se presenta la equivocación.
Respuesta: José tiene ____ mangos
23veintitrés
B José tenía 20 mangos y compró 5 mangos más.
¿Cuántos mangos tiene José ahora?
2 Calcule las siguientes sumas.
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
20 + 5
Planteamiento de la operación: 20 + 5 = ____
D U
2 0
D U
5
D U
2 5+ =
José
(1) 20 + 2 = ___ (2) 30 + 1 = ___ (3) 40 + 8 = ___
(4) 60 + 5 = ___ (5) 40 + 4 = ___ (6) 50 + 3 = ___
(7) 70 + 6 = ___ (8) 10 + 8 = ___ (9) 80 + 8 = ___
(10) 20 + 3 = ___ (11) 50 + 7 = ___ (12) 90 + 2 = ___
25
25
(2/3)
22 31 48
65 44 53
76 18 88
23 57 92

53. Unidad 3 - Suma34
SumemosLección 1:
(3/3)
Objetivo:
Materiales:
• Realizar los cálculos del tipo U + D0.
(M) azulejos
(N) azulejos
1. Comentar la situación del
problema. [C]
* Orientar para que piensen con
cuál operación se puede en�
contrar el resultado.
2. Escribir el planteamiento
de la operación. [C1]
M: ¿Cómo será el planteamiento
de la operación? Escríbanlo
en sus cuadernos.
Que se den cuenta que este caso
es muy parecido al anterior. La
diferencia es que aquí el primer
sumando que no tiene decena.
3. Encontrar la manera de cal-
cular. [C2]
* Indicar que utilicen los azule�
jos para resolver.
M: ¿Cómo hicieron?
RP: Representé con los azulejos
1 grupo de 7, que es la canti�
dad de naranjas que tenía Ra�
món y 2 grupos de 10, que son
las naranjas que compró des�
pués. Entonces tengo 1 grupo
de 7 y 2 grupos de 10, los jun�
té y me dio 27 naranjas.
4. Confirmar la manera de cal-
cular “7 + 20”.
M: ¿Por qué el resultado es vein�
tisiete? ¿Por qué lo escribi�
mos así?
* Concluir que en este caso,
para encontrar el resultado, se
procede igual que en el caso
anterior. Es necesario colocar
cada número en su lugar de
posición correspondiente.
* Resolver otros ejemplos para
afianzar el conocimiento.
5. Resolver el ejercicio 3 .
24 veinticuatro
C Ramón tiene 7 naranjas y compró 20 naranjas más.
¿Cuántas naranjas tiene Ramón ahora?
1 Escriba el planteamiento de la operación
2 Encuentre la respuesta.
3 Invente un problema usando 7 + 20.
7 + 20
D U
7
D U
2 0
D U
2 7+ =
3 Haga las siguientes sumas.
Tenía 7 naranjas Compró 20 naranjas más
Planteamiento de la operación: 7 + 20 = ____
naranjasRespuesta:
(1) 5 + 60 = ___ (2) 1 + 40 = ___ (3) 6 + 80 = ___
(4) 4 + 90 = ___ (5) 2 + 50 = ___ (6) 7 + 10 = ___
(7) 9 + 50 = ___ (8) 3 + 30 = ___ (9) 9 + 90 = ___
(10) 8 + 20 = ___ (11) 6 + 10 = ___ (12) 4 + 20 = ___
(3/3)
27
27
65 41 86
94 52 17
59 33 99
28 16 24

54. Guía para maestros/as- Matemática 20
Grado 35
Lección 2:
(1/4)
Objetivo:
Materiales:
Sigamos sumando
• Resolver en la forma vertical DU + DU sin reagrupar.
(M) azulejos
(N) azulejos
1. Comentar la situación del
problema. [A]
* Orientar para que piensen
con cuál operación se puede
encontrar el resultado.
2. Escribir el planteamiento
de la operación. [A1]
M: ¿Cómo será el planteamiento
de la operación? Escríbanlo
en sus cuadernos.
3. Encontrar la manera de cal-
cular. [A2]
M: Piensen en la manera de cal�
cular.
* Indicar que utilicen los azule�
jos para resolver.
* Dar el tiempo para la solución
individual.
* Indicar que presenten las opi�
niones.
Que se den cuenta que se
puede sumar por la posición.
4. Calcular en forma vertical.
* Escuchar las opiniones de los
niños y niñas.
* Si no surge la forma vertical,
presentarla.
* Concluir que para sumar en
forma vertical primero se su�
man las unidades y después
las decenas.
M: ¿Qué les parece esta forma?
Que se den cuenta que la for�
ma vertical facilita el cálculo
por la ubicación de los núme�
ros dependiendo del valor.
* Resolver otros ejemplos de�
sarrollando bien el proceso
del cálculo vertical por medio
de los azulejos.
5. Resolver el ejercicio 1 .
Es recomendable que los niños y las niñas usen un cua�
derno cuadriculado cuando hagan ejercicios adicionales,
para que no confundan las cifras de las D y las U al mo�
mento de escribir los números.
En este tipo de cálculo de la suma los niños y las niñas pueden encontrar
el resultado iniciando desde las decenas o calculando mentalmente por
que no se tiene que reagrupar, pero es recomendable que el maestro o la
maestra aclare el proceso desde donde se empieza a sumar (unidades).
25veinticinco
A Julia tenía 24 lápices y compró 15 lápices más.
¿Cuántos lápices tiene Julia ahora?
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
Tenía 24 lápices Compró 15 lápices más
D U
2 4
3 9
1 5
1.
2.
3.
(Cálculo)
24
15
39
+
1 Calcule cambiando a la forma vertical.
Lección 2: Sigamos sumando
24 + 15
Colocar los números en forma
vertical. Unidad debajo de unidad
y decena debajo de decena.
Se suman las unidades (U).
Se suman las decenas (D).
Planteamiento de la operación: 24 + 15 =
lápicesRespuesta: Julia tiene
(1) 13 + 21 = ___ (2) 25 + 53 = ___ (3) 18 + 31 = ___ (4) 61 + 24 = ___
(5) 72 + 21 = ___ (6) 54 + 23 = ___ (7) 44 + 25 = ___ (8) 21 + 17 = ___
D U D U D U D U
D U D U D U D U
39
(1/4)
39
34 78 49 85
93 77 69 38
1 3
2 1
3 4
2 5
5 3
7 8
1 8
3 1
4 9
6 1
2 4
8 5
7 2
2 1
9 3
5 4
2 3
7 7
4 4
2 5
6 9
2 1
1 7
3 8

55. Unidad 3 - Suma36
Sigamos sumandoLección 2:
(2/4)
• Resolver los cálculos operativos de D0 + DU y
DU + D0 sin reagrupar.
(M) azulejos
(N) azulejos
Objetivo:
Materiales:
1. Comentar la situación del
problema. [B]
* Orientar para que piensen
con cuál operación se puede
encontrar el resultado.
2. Escribir el planteamiento de
la operación. [B1]
* Indicar que escriban el plan�
teamiento de la operación en
sus cuadernos.
3. Calcular en forma vertical.
[B2]
M: Resuelvan de manera indivi�
dual utilizando los azulejos.
* Dar el tiempo suficiente has�
ta que todos los niños y niñas
terminen.
* Indicar que presenten sus tra�
bajos (incluyendo los errores
si los hay).
* En caso de que no salga una
buena justificación, el maes�
tro o la maestra podrá expli�
car usando los azulejos.
Que se den cuenta que para
el cálculo vertical es muy im�
portante la ubicación de los
números. (unidad debajo de
unidad y decena debajo de
decena)
4. Resolver el ejercicio 2 .
Aunque ya los niños y las niñas han aprendido la suma
con cero, es posible que cometan errores, por lo que se
debe prestar atención a este punto
B Carlos tiene 30 naranjas y compró 20 naranjas más.
¿Cuántas naranjas tiene Carlos en total?
26 veintiséis
RD
Tenía 30 naranjas Compró 24 naranjas más
Carlos
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
D U
3 0
5 4
2 4
Cálculo 30
24
54
+
2 Calcule cambiando a la forma vertical.
30 + 24
Planteamiento de la operación: 30 + 24 =
naranjasRespuesta:
(1) 13 + 40 = ___ (2) 50 + 18 = ___ (3) 20 + 57 = ___ (4) 60 + 29 = ___
(5) 76 + 20 = ___ (6) 59 + 40 = ___ (7) 40 + 25 = ___ (8) 30 + 51 = ___
D U D U D U D U
D U D U D U D U
54
(2/4)
54
53 68 77 89
96 99 65 81
1 3
4 0
5 3
5 0
1 8
6 8
2 0
5 7
7 7
6 0
2 9
8 9
7 6
2 0
9 6
5 9
4 0
9 9
4 0
2 5
6 5
3 0
5 1
8 1

56. Guía para maestros/as- Matemática 20
Grado 37
Sigamos sumandoLección 2:
(3/4)
• Resolver los cálculos operativos de DU + U sin reagrupar.
(M) azulejos
(N) azulejos
Objetivo:
Materiales:
1. Comentar la situación del
problema. [C]
* Orientar para que piensen
con cuál operación se puede
encontrar el resultado.
2. Escribir el planteamiento de
la operación. [C1]
* Indicar que escriban el plan�
teamiento de la operación en
sus cuadernos.
3. Calcular en forma vertical.
[C2]
M: Resuelvan de manera indivi�
dual utilizando los azulejos.
* Dar el tiempo suficiente has�
ta que todos los niños y niñas
terminen.
* Indicar que presenten sus tra�
bajos (incluyendo los errores
si los hay).
* En caso de que no salga una
buena justificación, el maes�
tro o la maestra podrá expli�
car usando los azulejos.
Que se den cuenta que este
tipo tiene alguna diferencia
con el anterior, ya que un
sumando no tiene decenas,
pero para resolver en forma
vertical se debe respetar la
misma regla para la ubica�
ción de los números. (unidad
debajo de unidad y decena
debajo de decena). (Véase
Notas)
4. Resolver el ejercicio 3 .
Es probable que algunos niños y niñas se equivoquen
colocando los números de esta manera:
En este caso, el maestro o la maestra deberá aclarar junto con los ni�
ños y niñas, usando los azulejos, haciendo preguntas, etc. hasta llegar
a la fórmula correcta.
14
+ 4
H
Rep. Dom.
H
H
Rep.Dom.
EL DEPORTE ES SALUD
Hay 14 niños en la cancha. Llegan 4 niños más.
H
C Hay 14 niños en la cancha y llegaron 4 niños más. ¿Cuántos niños hay en total?
27veintisiete
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
D U
1 4
1 8
4
Cálculo 14
4
18
+
3 Calcule cambiando a la forma vertical.
14 + 4
Planteamiento de la operación: 14 + 4 =
niñosRespuesta:
(1) 33 + 2 = ___ (2) 41 + 8 = ___ (3) 72 + 5 = ___ (4) 47 + 1 = ___
(5) 16 + 3 = ___ (6) 24 + 5 = ___ (7) 41 + 6 = ___ (8) 36 + 2 = ___
D U D U D U D U
D U D U D U D U
18
18
35 49 77 48
19 29 47 38
3 3
2
3 5
4 1
8
4 9
7 2
5
7 7
4 7
1
4 8
1 6
3
1 9
2 4
5
2 9
4 1
6
4 7
3 6
2
3 8
(3/4)

57. Unidad 3 - Suma38
Sigamos sumandoLección 2:
(4/4)
Es probable que algunos niños y niñas se equivoquen
colocando los números de esta manera:
Si esto ocurre, se debe aclarar junto con los niños y niñas, usando los
azulejos haciendo preguntas hasta llegar a la forma correcta.
3
+ 24
• Resolver los cálculos operativos de U + DU sin reagrupar.
(M) azulejos
(N) azulejos
Objetivo:
Materiales:
1. Comentar la situación del
problema. [D]
* Orientar para que piensen
con cuál operación se puede
encontrar el resultado.
2. Escribir el planteamiento de
la operación. [D1]
* Indicar que escriban el plan�
teamiento de la operación en
sus cuadernos.
3. Calcular en forma vertical.
[D2]
M: Resuelvan de manera indivi�
dual utilizando los azulejos.
* Dar el tiempo suficiente has�
ta que todos los niños y niñas
terminen.
* Indicar que presenten sus tra�
bajos (incluyendo los errores
si los hay).
* En caso de que no salga una
buena justificación, el maes�
tro o la maestra podrá expli�
car usando los azulejos.
Que se den cuenta que este
tipo de sumas es semejante
al de la clase anterior y se
deben tener en cuenta las
mismas observaciones para
la ubicación de los números.
(unidad debajo de unidad y
decena debajo de decena)
4. Resolver el ejercicio 4 .
28 veintiocho
D Hay 3 patitos en el lago y están llegando 24 más. ¿Cuántos patitos hay en total?
Están llegando 24 patitos másHay 3 patitos en el lago
4 Calcula cambiando a la forma vertical.
(1) 8 + 21 = ___ (2) 4 + 63 = ___ (3) 7 + 41 = ___ (4) 3 + 35 = ___
(5) 3 + 52 = ___ (6) 2 + 94 = ___ (7) 5 + 82 = ___ (8) 8 + 31 = ___
D U D U D U D U
D U D U D U D U
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
3 Invente otro problema utilizando 3 + 24.
Cálculo
3
24
27
+
3 + 24
Planteamiento de la operación: 3 + 24 =
patitosRespuesta:
D U
3
2 7
2 4
29 67 48 38
55 96 87 39
8
2 1
2 9
4
6 3
6 7
7
4 1
4 8
3
3 5
3 8
3
5 2
5 5
2
9 4
9 6
5
8 2
8 7
8
3 1
3 9
27
27
(4/4)

58. Guía para maestros/as- Matemática 20
Grado 39
Ejercicios (1)Unidad 3:
(1/1)
• Confirmar lo aprendido en la lección 2.Objetivo:
Materiales:
Los ejercicios tratan sobre:
1 Ejercicios del cálculo verti�
cal sin reagrupar.
2 Ejercicios para confirmar
el valor posicional.
3 Problemas de aplicación.
4 Construcción de problemas
donde se aplique la suma.
Ejercicios (1)
1 Calcule las siguientes sumas.
2 Calcule las siguientes sumas.
3 Resuelva.
(1) Pablo tenía 25 bellugas y Angel le regaló 24 más.
¿Cuántas bellugas tiene ahora Pablo?
Cálculo
En un jardín hay 44 rosas rojas y 3 rosas amarillas.
¿Cuántas rosas hay en total en el jardín?
4 Invente problemas de los siguientes planteamientos y resuélvalos.
(1) 23 + 51 (2) 60 + 9
(3) 3 + 25 (4) 42 + 7
6
+ 27
Planteamiento de la operación:___________________
Respuesta: ______ bellugas.
21
55+
64
35+
53
4+
72
6+
29veintinueve
(1) 21 + 55 = ___ (2) 64 + 35 = ___ (3) 53 + 4 = ___ (4) 72 + 6 = ___
(1) 42 + 46 = ___ (2) 30 + 55 = ___ (3) 10 + 48 = ___ (4) 54 + 20 = ___
(5) 56 + 1 = ___ (6) 61 + 8 = ___ (7) 4 + 62 = ___ (8) 14 + 3 = ___
(2)
Cálculo
Planteamiento de la operación:___________________
Respuesta: ______ rosas en total.
76 99 57 78
(1/1)
76 99 57 78
42
88
46+
30
85
55+
10
58
48+
54
74
20+
88 85 58 74
56
57
1+
61
69
8+
4
66
62+
14
17
3+
57
25 + 24 = 49
69 66 17
25
49
49 24+
44 + 3 = 47
44
47
47
Se omite la solución
3+

59. Unidad 3 - Suma40
Sumemos reagrupandoLección 3:
(1/7)
• Resolver los cálculos operativos de DU + DU reagrupando.
(M) azulejos
(N) azulejos
Objetivo:
Materiales:
1. Comentar la situación del
problema. [A]
M: ¿Cómo se puede resolver el
problema?
2. Escribir el planteamiento de
la operación. [A1]
* Indicar a los niños y a las niñas
que escriban el planteamiento
de la operación.
3. Encontrar la manera de cal-
cular. [A2]
* Indicar que calculen individual�
mente utilizando los azulejos.
* Orientar a los niños y a las ni�
ñas que tienen problemas, para
que piensen sobre el cálculo de
“8+4”.
* Indicar que presenten las opi�
niones.
RP: Primero sumé las unidades, me
dio 12. Como en 12 hay una de�
cena y dos unidades entonces,
pasé la decena a su posición
y me quedó 2 unidades; luego
sumé 2 decenas que hay, más
1 decena que pasé. Son 3 de�
cenas. El resultado es 3 dece�
nas y 2 unidades, que es igual
a 32 unidades.
* Si no sale la respuesta espe�
rada el maestro o la maestra
puede inducirlos.
4. Confirmar la manera del cál-
culo vertical con los núme-
ros.
* Escribir en la pizarra en la for�
ma vertical “18+14”.
* Explicar la importancia del nú�
mero auxiliar (véase notas).
* Indicar que hagan el cálculo
siguiendo el proceso que rea�
lizaron con los azulejos.
* Concluir aclarando los pasos
que se siguen para calcular
reagrupando a la decena.
5. Resolver el ejercicio 1 .
El número que se reagrupa en las decenas es un núme�
ro cuya escritura es opcional ya que muchos niños/as
no nececitarán escribirlo. Sin embargo, hay otros niños
a los que se les dificulta, por lo que éstos lo escriben.
A Dany tiene 18 mentas y Angela tiene 14 mentas ¿Cuántas mentas tienen entre los dos?
Lección 3: Sumemos reagrupando
1 Escriba el planteamiento de la operación.
2 Encuentre la manera de resolver.
1 Resuelva los siguientes ejercicios.
Plateamiento de la operación: 18 + 14 =
Respuesta: Tienen mentas.
1
2
3
Colocar los números ordenada-
mente (en cada posición).
Se suman las unidades:
8 + 4 = 12, hay 12 unidades, 10
de ellas forman 1 decena. Ahora
hay 1 decena y 2 unidades, se
traslada la decena a la posición
de las decenas (D), quedan 2
unidades (U).
Se suman las decenas:
1 + 1 + 1 = 3, el resultado es 32.
18 + 14
30 treinta
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
O
NFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
O
NFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
O
NFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
FRE
SA
C
ONFITES
C
O
NFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
Dany tiene 18 mentas Angela tiene 14 mentas
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
C
ONFITES
Lim
on
28
13+
57
26+
34
17+
24
39+
(1) 28 + 13 = ___ (2) 57 + 26 = ___ (3) 34 + 17 = ___ (4) 24 + 39 = ___
39
24+
53
38+
25
57+
26
46+
(5) 39 + 24 = ___ (6) 53 + 38 = ___ (7) 25 + 57 = ___ (8) 26 + 46 = ___
D U
1 8
1 4
D U
1 8
1 4
2
D U
1 8
1 4
23
1
1
18
14+
18
14
32
+
1
18
14
2
+
1
2
2
1
2
3
32
32
(1/7)
41 83 51 63
41 83 51 63
63 91 82 72
63 91 82 72
1 1 1 1
1 1 1 1

60. Guía para maestros/as- Matemática 20
Grado 41
Sumemos reagrupandoLección 3:
(2/7~3/7)
• Resolver los cálculos operativos de DU+DU=D0
reagrupando y practicar el cálculo del tipo DU+DU.
Objetivo:
Materiales:
1. Comentar la situación del
problema. [B]
M: ¿Cómo se puede resolver la
situación que presenta el pro�
blema?
2. Escribir el planteamiento de
la operación. [B1]
M: ¿Cómo se plantea la opera�
ción? Escríbanlo en sus cua�
dernos.
3. Calcular en forma vertical.
[B2]
* Indicar que escriban la ope�
ración en forma vertical y que
resuelvan individualmente.
* Garantizar el tiempo suficien�
te para que todos y todas ter�
minen.
* Si ya los niños y niñas pueden
hacer los cálculos sin necesi�
dad de los azulejos, entonces
no hay que utilizarlos.
4. Explicar la manera de resol-
ver.
* Indicar que presenten su tra�
bajo en la pizarra y que expli�
quen paso a paso.
* Hacer las explicaciones y acla�
raciones necesarias.
* Confirmar que se escribe el nú�
mero que se reagrupa encima
de las decenas.
* Realizar otros ejercicios.
5. Resolver el ejercicio 2 .
(M) azulejos
(N) azulejos
B El lunes, Kike cortó 37 sandías y el martes 43.
¿Cuántas sandías cortó en los dos días?
1 Escriba el planteamiento de la operación:
2 Encuentre la respuesta
Planteamiento de la
operación: 37 + 43 =
37 + 43
Cálculo
37
43+
1
2 Calcule las siguientes sumas.
31treinta y uno
D U
3 7
4 3
D U
3 7
4 3
0
D U
3 7
4 3
08
1
1
3 7
4 3+
37
43
80
+
1
37
43
0
+
1
Respuesta: sandías.
18
42+
54
26+
69
11+
31
29+
(1) 18 + 42 = ___ (2) 54 + 26 = ___ (3) 69 + 11 = ___ (4) 31 + 29 = ___
33
37+
65
25+
12
18+
26
34+
(5) 33 + 37 = ___ (6) 65 + 25 = ___ (7) 12 + 18 = ___ (8) 26 + 34 = ___
LUNES MARTES
Cortó 37 sandías. Cortó 43 sandías.
80
(2/7~3/7)
80
80
60 80 80 60
60 80 80 60
70 90 30 60
70 90 30 60
1 1 1 1
1 1 1 1
[Hasta aquí 2/7]
[Desde aquí 3/7]

61. Unidad 3 - Suma42
Sumemos reagrupandoLección 3:
(2/7~3/7)
6. Resolver los ejercicios 3 ,
4 y 5 .
* Estos ejercicios son para
afianzar el cálculo y la aplica�
ción de la suma reagrupando
antes de trabajar con los tipos
de DU+U y U+DU.
* Se puede repasar el proceso
de cálculo de la suma �������reagru�
pando�����������������������desarrollando un ejem�
plo antes de hacer los ejerci�
cios.
Los ejercicios tratan sobre:
3 Ejercicios del cálculo de la
suma reagrupando (DU+DU,
DU+DU=D0)
4 Problemas de aplicación
5 Construcción de pro�
blemas donde se aplique la
suma reagrupando.
[Continuación]
4 Resuelva los siguientes problemas.
5 Invente problemas de los siguientes planteamientos y resuélvalos.
(1) Tomás tiene 43 postalitas y Elvis le regala 28 postalitas más.
¿Cuántas postalitas tiene Tomás en total?
(2) En el primer viaje una guagua transportó 34 pasajeros y en el
segundo viaje transportó 36 pasajeros. ¿Cuántos pasajeros
transportó en total?
Planteamiento de la operación:___________________
Respuesta: postalitas.
Planteamiento de la operación:___________________
Respuesta: pasajeros.
Cálculo
Cálculo
32 treinta y dos
(1) 25 + 26 (2) 28 + 39 (3) 53 + 17
3 Haga los cálculos de las siguientes sumas.
28
55+
(1) 28 + 55 = ___ (2) 36 + 48 = ___ (3) 29 + 44 = ___ (4) 27 + 63 = ___
(5) 78 + 15 = ___ (6) 61 + 19 = ___ (7) 38 + 59 = ___ (8) 24 + 36 = ___
(9) 47 + 27 = ___ (10) 62 + 28 = ___ (11) 33 + 39 = ___ (12) 55 + 25 = ___
4 3
+ 2 8
7 1
1
3 4
+ 3 6
7 0
1
43 + 28 = 71
71
34 + 36 = 70
70
Se omite la solución
83
36
84
48+
29
73
44+
27
90
63+
83 84 73 90
78
93
15+
61
80
19+
38
97
59+
24
60
36+
93 80 97 60
1 1 1 1
1 1 1 1
47
74
27+
62
90
28+
33
72
39+
55
80
25+
74 90 72 80
1 1 1 1

62. Guía para maestros/as- Matemática 20
Grado 43
Sumemos reagrupandoLección 3:
(4/7)
• Resolver cálculos operativos del tipo DU+U reagrupando.Objetivo:
Materiales:
1. Comentar la situación del
problema. [C]
M: ¿Con cuál operación pode�
mos encontrar el resultado?
2. Escribir el planteamiento de
la operación. [C1]
* Indicar que escriban el plan�
teamiento de la operación.
3. Encontrar la manera de cal-
cular. [C2]
* Indicar que resuelvan indivi�
dualmente.
M: ¿Qué cuidado se debe tener
al escribir en forma vertical?
RP: Colocar bien los números.
(unidades debajo de las unida�
des y decenas debajo de las
decenas)
* Informar que el número 1 que
se reagrupa, en caso de se
escriba debe ser en la parte
superior de los números que
están en la siguiente posición.
* Pedirles que presenten sus
resultados.
* Hacer las aclaraciones y ex�
plicaciones necesarias.
* Desarrollar otros ejemplos para
afianzar los conocimientos.
4. Resolver los ejercicios 6 y 7 .
* Indicar que resuelvan sólo con
los números en caso de que
haya dificultad puede usar los
azulejos y/o auxiliarse de la ta�
bla de valores.
C ¿Cuántos libros hay en total?
1 Escriba el planteamiento de la operación:
2 Encuentre la respuesta.
27 + 7
Librero No 1 Librero No 2
En este librero
hay 27 libros.
En este librero
hay 7 libros.
6 Calcule las siguientes sumas.
7 Calcule cambiando a la forma vertical.
33treinta y tres
Planteamiento de la
operación: 27 + 7 =
Cálculo
27
7
34
+
1
Respuesta: libros.
35
9+
16
5+
26
4+
42
8+
(1) 35 + 9 = ___ (2) 16 + 5 = ___ (3) 26 + 4 = ___ (4) 42 + 8 = ___
(1) 63 + 8 = ___ (2) 54 + 9 = ___ (3) 35 + 5 = ___ (4) 27 + 6 = ___
(5) 49 + 6 = ___ (6) 64 + 7 = ___ (7) 73 + 8 = ___ (8) 26 + 4 = ___
44 21 30 50
44 21 30 50
1 1 1 1
63
71
8+
54
63
9+
35
40
5+
27
33
6+
71 63 40 33
1 1 1 1
49
55
6+
64
71
7+
73
81
8+
26
30
4+
55 71 81 30
1 1 1 1
(4/7)
34
34

63. Unidad 3 - Suma44
Sumemos reagrupandoLección 3:
(5/7)
• Resolver cálculos operativos del tipo U+DU reagrupando.Objetivo:
Materiales:
1. Comentar la situación del
problema. [D]
M: ¿Cómo se puede resolver el
problema?
2. Escribir el planteamiento de
la operación. [D1]
* Indicar que escriban el plan�
teamiento de la operación.
3. Encontrar la manera de cal-
cular. [D2]
* Indicar que resuelvan indivi�
dualmente.
* Recordar los puntos que se de�
ben tener presentes para escribir
y calcular en la forma vertical.
* Desarrollar otros ejemplos para
afianzar los conocimientos.
4. Resolver los ejercicios 8 y 9 .
D Hay 8 pollitos en el estanque y 14 pollitos están llegando.
¿Cuántos pollitos hay en total?
1 Escriba el planteamiento de la operación:
2 Encuentre la respuesta.
8 + 14
Hay 8 pollitos en el estanque. 14 pollitos están llegando al estanque.
34 treinta y cuatro
Planteamiento de la
operación: 8 + 14 =
Cálculo
8
14
22
+
1
Respuesta: pollitos.
8 Calcule las siguientes sumas.
9 Calcule las siguientes sumas.
8
85+
6
29+
2
38+
4
87+
(1) 8 + 85 = ___ (2) 6 + 29 = ___ (3) 2 + 38 = ___ (4) 4 + 87 = ___
(1) 3 + 58 = ___ (2) 8 + 36 = ___ (3) 5 + 55 = ___ (4) 9 + 39 = ___
(5) 4 + 36 = ___ (6) 9 + 37 = ___ (7) 7 + 18 = ___ (8) 2 + 48 = ___
(5/7)
22
22
93 35 40 91
93 35 40 91
1 1 1 1
3
61
58+
8
44
36+
5
60
55+
9
48
39+
71 44 60 48
1 1 1 1
4
40
36+
9
46
37+
7
25
18+
2
50
48+
40 46 25 50
1 1 1 1

64. Guía para maestros/as- Matemática 20
Grado 45
Sumemos reagrupandoLección 3:
(6/7)
• Resolver cálculos operativos del tipo DU+DU=CDU
reagrupando una vez.
Objetivo:
Materiales: (M) azulejos
(N) azulejos
1. Comentar la situación del
problema. [E]
M: ¿Cómo se puede resolver el
problema?
2. Escribir el planteamiento de
la operación. [E1]
* Indicar a los niños y a las niñas
que escriban el planteamiento
de la operación.
3. Encontrar la manera de cal-
cular. [E2]
* Indicar que calculen individual�
mente utilizando los azulejos.
Que se den cuenta que al su�
mar las decenas el resultado es
11 por lo que hay que convertir
10 decenas a una centena.
* Indicar que presenten sus
opiniones.
RP: Primero sumé las unidades
me dio 9, Luego sumé las
decenas, pero como me dió
11 decenas, entonces debo
cambiar 10 decena por una
centena y me queda 1 dece�
na, por último bajé la centena
y el resultado es 1 centena, 1
decena y 9 unidades; es decir,
119 unidades.
* Si no sale la respuesta espe�
rada el maestro o la maestra
puede inducirlas.
4. Confirmar la manera del cálcu-
lo vertical con los números.
* Escribir en la pizarra en la for�
ma vertical “65+54”.
* Confirmar en la pizarra el pro�
ceso seguido, utilizando los
azulejos.
* Hacer los cálculos siguiendo
el proceso que realizaron con
los azulejos.
* Concluir aclarando los pasos
que se siguen para calcular
reagrupando a la centena.
5. Resolver el ejercicio 10 .
E Tenía 65 huevos y compró 54 huevos. ¿Cuántos huevos tiene Pedro ahora?
Tenía 65 huevos Compró 54 huevos más
HuevosHuevos
Dominicanos
10 Resuelva los siguientes ejercicios.
treinta y cinco 35
1
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
65 + 54
Planteamiento de la operación: 65 + 54 =
huevosRespuesta:
DC U
5
11 9
5
6
4
Cálculo
65
54+
65
54
9
+
65
54
119
+
1
(1) 84 + 63 = ___ (2) 71 + 46 = ___ (3) 93 + 52 = ___ (4) 95 + 81 = ___
84
63+
71
46+
93
52+
95
81+
(5) 40 + 63 = ___ (6) 59 + 60 = ___ (7) 42 + 91 = ___ (8) 55 + 53 = ___
40
63+
59
60+
42
91+
55
53+
119
(6/7)
119
147 117 145 176
147
1
117
1
145
1
176
1
103 119 133 108
103
1
119
1
133
1
108
1

65. Unidad 3 - Suma46
Sumemos reagrupandoLección 3:
(7/7)
• Resolver cálculos operativos del tipo DU+DU=CDU
reagrupando dos veces.
Objetivo:
Materiales:
1. Comentar la situación del
problema. [F]
M: ¿Con cuál operación encon�
tramos el resultado?
2. Escribir el planteamiento de
la operación. [F1]
* Indicar que escriban el plan�
teamiento de la operación.
3. Encontrar la manera de cal-
cular. [F2]
* Indicar que resuelvan indivi�
dualmente.
M: ¿Qué cuidado se debe tener
al escribir en forma vertical?
RP: Colocar bien los números. (uni�
dades debajo de las unidades y
decenas debajo de las decenas)
Que se den cuenta que en este
caso deben reagrupar dos veces.
* Recordar que deben colocar
bien el número que se reagru�
pa y que se debe sumar en la
siguiente posición.
* Pedirles que presenten sus
resultados.
* Hacer las aclaraciones y ex�
plicaciones necesarias.
* Desarrollarotrosejemplospara
afianzar los conocimientos.
4. Resolver los ejercicios 11 y 12 . (10) 44 + 68 = ___ (11) 29 + 71 = ___ (12) 55 + 47 = ___
12 Resuelva el siguiente problema.
Planteamiento la operación:___________________
Respuesta: estudiantes.
F Karina tiene 74 guineos y Zulema tiene 69.
¿Cuántos guineos tienen Karina y Zulema en total?
1 Escriba el planteamiento de la operación
2 Encuentre la respuesta.
74 + 69
36 treinta y seis
(1) En la escuela hay 87 varones y 65 hembras.
¿Cuántos estudiantes hay en total?
Cálculo
74
69+
Planteamiento de la operación: 74 + 69 =
Respuesta: guineos.
11 Resuelva los siguientes ejercicios.
(1) 49 + 82 = ___ (2) 59 + 71 = ___ (3) 68 + 74 = ___ (4) 77 + 83 = ___
49
82+
(5) 58 + 64 = ___ (6) 79 + 45 = ___ (7) 39 + 64 = ___ (8) 81 + 99 = ___
Cálculo
ZulemaKarina
Karina tiene 74 guineos Zulema tiene 69 guineos
(9) 37 + 68 = ___
143
11
143
143
(7/7)
131 130 142 160
131
1 1
122 124 103 180
59
130
71+
1 1
68
142
74+
1 1
77
160
83+
1 1
58
122
64+
1 1
79
124
45+
1 1
39
103
64+
1 1
81
180
99+
1 1
87 + 65 = 152
152
87
152
65+
1 1
105 112 100 102
37
105
68+
1 1
44
112
68+
1 1
29
100
71+
1 1
55
102
47+
1 1

66. Guía para maestros/as- Matemática 20
Grado 47
Ejercicios (2)Unidad 3:
(1/1)
• Confirmar lo aprendido en la lección 3.Objetivo:
Materiales:
Los ejercicios tratan sobre:
1 Cálculo de la suma re�
agrupando.
2 Problemas de aplicación.
Ejercicios (2)
1 Resuelva las siguientes sumas cambiando a la forma vertical.
2 Resuelva los siguientes problemas.
treinta y siete 37
(10) 34 + 9 = ___ (11) 26 + 93 = ___ (12) 75 + 39 = ___
(1) 34 + 18 = ___ (2) 55 + 37 = ___ (3) 29 + 34 = ___ (4) 48 + 22 = ___
34
18+
(5) 35 + 16 = ___ (6) 6 + 37 = ___ (7) 26 + 4 = ___ (8) 8 + 87 = ___
(9) 37 + 29 = ___
Planteamiento la operación:_______________
Respuesta: bolas.
(1) En una canasta hay 27 bolas rojas y 25 azules.
¿Cuántas bolas hay en total?
Cálculo
Planteamiento la operación:_______________
Respuesta: pesos.
(2) Julia tiene 48 pesos y su tío le regala 85 pesos más.
¿Cuántos pesos tiene Julia en total?
Cálculo
Planteamiento la operación:_______________
Respuesta: peces.
(3) Mi hermano y yo fuimos de pesca. Mi hermano pescó
8 peces y yo 17 peces. ¿Cuántos peces pescamos
entre los dos? Cálculo
27
52
25+
1
48
133
85+
11
8
25
17+
1
27 + 25 = 52
52
48 + 85 = 133
133
8 + 17 = 25
25
66 43 119 114
37
66
29+
1
34
43
9+
1
26
119
93+
1 1
75
114
39+
1 1
51 43 30 95
35
51
16+
1
6
43
37+
1
26
30
4+
1
8
95
87+
1
(1/1)
52 92 63 70
52
1
55
92
37+
1
29
63
34+
1
48
70
22+
1

67. Unidad 3 - Suma48
Ejercicios (3)Unidad 3:
(1/2~2/2)
• Confirmar lo aprendido en toda la unidad.Objetivo:
Materiales:
Los ejercicios tratan sobre:
1 Ejercicios de cálculos de
todos los tipos; reagrupar y
reagrupando
2 Ejercicios de dominio y
comprensión
3 Problemas de aplicación
Continúa en la siguiente página…
2 Encuentre el número que falta en cada suma.
(1) 4 6
3 2
7
+
(5) 5
2 6
8 2
+
(2) 1 5
9
4
+
(6)
+
(3) 3 8
8
8 6
+
(7) 1
2 4
4 2
+
(4)
3 6
3 9
+
(8) 3
8
8 1
+
Ejercicios (3)
38 treinta y ocho
7
3
6 0
1 Calcule las siguientes sumas.
(10) 8 + 88 = ___ (11) 44 + 26 = ___ (12) 45 + 66 = ___
(1) 12 + 19 = ___ (2) 27 + 3 = ___ (3) 26 + 42 = ___ (4) 17 + 33 = ___
(5) 1 + 69 = ___ (6) 57 + 6 = ___ (7) 29 + 36 = ___ (8) 8 + 22 = ___
(9) 43 + 51 = ___
3 Resuelva los siguientes problemas.
Planteamiento la operación:_______________
Respuesta: páginas.
(1) María leyó 38 páginas de un libro ayer, y hoy leyó 50
páginas más. ¿Cuántas páginas leyó durante los dos días?
Cálculo
Planteamiento la operación:_______________
Respuesta: pesos.
(2) José pagó 35 pesos por un cuaderno y 8 por un lápiz.
¿Cuántas pesos gastó José en total?
Cálculo
35
43
8+
1
6
8 2
5
4
8
3
7
(1/2 ~2/2)
31 30 68 50
12
31
19+
1
70 63 65 30
27
30
3+
1
26
48
42+
17
50
33+
1
1
70
69+
1
57
63
6+
1
29
65
36+
1
8
30
22+
1
94 43 70 111
43
94
51+
8
96
88+
1
44
70
26+
1
45
111
66+
1 1
38 + 50 = 88
88
38
52
50+
35 + 8 = 43
43
[Hasta aquí 1/2]
[Desde aquí 2/2]

68. Guía para maestros/as- Matemática 20
Grado 49
[Continuación]
Ejercicios (3)Unidad 3:
(1/2~2/2)
...viene de la página anterior.
Los ejercicios tratan sobre:
4 Ejercicios de cálculos de
todos los tipos: sin reagrupar y
reagrupando.
5 Ejercicios de dominio y
comprensión.
6 Problemas de aplicación.
treinta y nueve 39
4 Calcule las siguientes operaciones.
6(7)
2
3 8
+
6(3)
3
5
8 9
+
3(8)
4 8
8 3
+
7
(4)
3
4 1
+
32(6)
3
6 0
+
1(2)
9
2
6 0
+
6
5(5)
3+
(1)
8
4
8
7
+
Resuelva los siguientes problemas.6
5 Encuentre el número que falta en cada suma.
(10) 30 + 62 = ___ (11) 47 + 33 = ___ (12) 7 + 68 = ___
(1) 26 + 45 = ___ (2) 71 + 13 = ___ (3) 61 + 9 = ___ (4) 15 + 47 = ___
(5) 19 + 39 = ___ (6) 53 + 8 = ___ (7) 73 + 62 = ___ (8) 64 + 20 = ___
(9) 44 + 55 = ___
Planteamiento la operación:_______________
Respuesta: lápices.
(1) Laura tenía 24 lápices y su padre le regaló 18 lápices más
¿Cuántos lápices tiene ahora Laura en total?
Cálculo
Planteamiento la operación:_______________
Respuesta: vehículos.
(2) En el parqueo del supermercado hay 37 carros y 9
camionetas. ¿Cuántos vehículos hay en total en el
parqueo?
Cálculo
71 84 70 62
26
71
45+
1
71
84
13+
61
70
9+
15
62
47+
11
58 61 135 84
19
58
39+
1
53
61
8+
1
73
135
62+
1
64
84
20+
99 92 80 75
44
99
55+
30
92
62+
47
80
33+
1
7
75
68+
1
2
1
3
5
4
7
3
1
4
8
0
24 + 18 = 42
42
24
42
18+
37 + 9 = 46
46
37
46
9+
1
1

69. Unidad 4 - Resta50
• Realizan sustracciones donde el minuendo es menor que 100.
• Resuelven problemas de la vida cotidiana aplicando resta con minuendo menor que 100, sin reagru-
par y reagrupando.
Resta
Expectativas de logro
(15 horas)Unidad
1
44
Números hasta 999 Números hasta 9,999 Números hasta 1,000,000Números hasta 9
Relación y desarrollo2
Resta (1)
Sustracción cuyo minuen-
do sea menor o igual
que 9 y mayor o igual al
sustraendo
• Sentido de la resta
(“quitar” y “diferencia”)
• Operación de la resta
cuyo minuendo sea
menor o igual que 9 y
mayor o igual al sus-
traendo.
• Planteamiento de la
operación.
• Procedimiento de ope-
ración.
Resta
Sustracción cuyo minuen-
do sea menor que 100
• DU – DU, U, sin
reagrupar(todos los
casos).
• Procedimiento de la
adición vertical.
• DU – DU, U,
reagrupando(todos los
casos).
Sustracción
Sustracción con minuen-
dos menores que 1,000
• CDU – CDU, DU, U,
sin reagrupar (todos los
casos).
• CDU – CDU, DU, U,
reagrupando de las de-
cenas (todos los casos).
• CDU – CDU, DU,
reagrupando de las cen-
tenas (todos los casos).
• CDU – CDU, DU, U,
reagrupando dos veces
de las centenas y de
las centenas (todos los
casos).
Adición y sustracción
Adición y sustracción con
números menor o igual
que 1,000,000
Aproximación de adición y
sustracción
Números hasta 19
Suma y resta combinada
• Suma con tres suman-
dos.
• Resta con tres sus-
traendos.
• Suma y resta combina-
das. Operaciones combinadas
• Orden de cálculo.
• Uso de paréntesis.
• Propiedad asociativa de
la adición.
• Propiedad asociativa de
la multiplicación.
Resta (2)
Sustracción cuyo minuen-
do sea menor o igual que
18 y mayor al sustraendo
• (10 hasta 18) - U re-
agrupando.
Números hasta 99

70. Guía para maestros/as - Matemática 20
Grado 51
Puntos de lección
• Lección 1: Restemos
Se introduce la resta en forma horizontal para
que los niños y las niñas desarrollen el cálculo
mental imaginando la construcción de núme-
ros con las operaciones fáciles.
Lección 2: Sigamos Restando
En esta lección se pretende que los niños y
las niñas comprendan la forma operativa ver-
tical de DU – DU sin reagrupar. Que capten
la construcción de números de DU (con “can-
tidades” en las posiciones de las decenas y
de las unidades) haciendo énfasis en la nece-
sidad de pensar sobre la forma operativa de
realizar el cálculo.
• Lección 3: Restemos reagrupando
En el 1er grado los niños y las niñas apren-
dieron la sustracción del tipo DU – U reagru-
pando. Aplicando este aprendizaje deberán
resolver DU – DU reagrupando. Hay que ejer-
citarlos con suficientes ejemplos tomando en
cuenta los diferentes tipos de cálculos. Este
mecanismo es la base del cálculo de la resta
reagrupando.
4
1/4~2/4 • Operación del tipo D0–D0=D0
3 Plan de estudio (15 horas)
1. Restemos.
(4 horas)
2. Sigamos restando
(4 horas)
3/4 • Operación del tipo DU–D0=U
4/4 • Operación del tipo DU–U=D0
1/4 • Operación del tipo DU–DU=DU sin reagrupar, forma
vertical
2/4 • Operación del tipo DU–DU=U sin reagrupar, forma
vertical
3/4
1/1 • Aplicación y dominio de la lección 2 Ejercicios (1) (1 hora)
3. Restemos reagrupando
(4 horas)
1/4 • Operación del tipo DU–DU=DU reagrupando
2/4 • Operación del tipo D0–DU=DU reagrupando
3/4 • Operación del tipo DU–DU=U y D0–DU=U
reagrupando
4/4 • Operación del tipo DU–U=DU y D0–U=DU
reagrupando
1/1 • Aplicación y dominio de la lección 3 Ejercicios (2) (1 hora)
1/1 • Ejercicios de toda la unidad Ejercicios (3) (1 hora)
4/4 • Forma de resolver problemas y su procedimiento
• Operación del tipo DU–U=DU sin reagrupar, forma
vertical

71. Unidad 4 - Resta52
El dominó como recurso didáctico
Es un material usado para el entretenimiento o juego. Con él podemos recordar y reforzar lo aprendi-
do en una lección dada, así como desarrollar actitudes de colaboración, compañerismo, honestidad,
perseverancia, participación y agilidad en el jugador, en forma divertida. También permite conectar lo
aprendido con nuevos desafíos y que el alumno/a auto evalúe su propio aprendizaje. Es un juego de
mesa que desarrolla el trabajo en equipo.
Elaboración de las fichas:
Las fichas deben ser rectangulares, divididas en dos cuadrados. En cada una de las partes se indican
valores o expresiones según los fines del mismo. Las fichas deben mantener algunas características
comunes entre ellas, como son: Igual color, forma, tamaño, texturas,... de ese modo evitamos que las
mismas sean conocidas previamente por los jugadores. La cantidad de fichas a elaborar dependerá del
tiempo que se estime invertir en dicho juego. Un juego de dominó puede ser elaborado con 3, 6, 10,
15, 21, 28, 36... fichas. Sólo se trata de descubrir la regla que se esconde. Más abajo colocaremos un
gráfico explicativo.
Elaboración de las combinaciones en el contenido de las fichas:
Los contenidos de las fichas varían según la intensión del juego. En este caso particular relacionare-
mos los que se usan en los juegos de dominó tradicionales usando números del 0 al 6 y el cálculo de
la resta con algunos de sus resultados. Sin embargo, después de aprender a construirlo pueden abor-
darse temas diversos.
Reagrupar
DU–DU=DU (31–14=17)
DU–DU=U (25–17=8)
DU–U=DU (22–5=17)
Tipos de la resta en el cálculo vertical
Los maestros y las maestras deben estar conscientes de la clasificación al elaborar los ejercicios que
presentarán a los niños y niñas. Se deben inventar los ejercicios de los diferentes tipos, fijándose en
los ejemplos que están entre los paréntesis.
DU–DU=DU (36–13=23)
DU–D0=DU (27–10=17)
DU–DU=U (23–21=2)
DU–D0=U (39–30=9)
DU–U=DU (62–1=61)
DU–0=DU (32–0=32)
DU–DU=D0 (23–13=10)
D0–D0=D0 (30–20=10)
DU–DU=0 (36–36=0)
D0–D0=0 (30–30=0)
DU–U=D0 (38–8=30)
D0–0=D0 (20–0=20)
D0–DU=DU (30–14=16)
D0–DU=U (20–14=6)
D0–U=DU (20–9=11)
Sin reagrupar
2)
4)
6)
8)
10)
12)
1)
3)
5)
7)
9)
11)
2)
4)
6)
1)
2)
3)
Columnas
1
2
A
B

72. Guía para maestros/as - Matemática 20
Grado 53
Cómo se juega dominó
1. Las fichas tienen dos caras, algunas caras son iguales, semejantes o equi-
valentes (estas son fichas llamadas Dobles). Otras son de caras diferentes,
conocidas como fichas de dos caras fraccionarias.
2. El esquema de la izquierda muestra un triángulo rectángulo con fichas or-
denadas con la características de que las caras que forman la base del
triángulo son de igual valor o equivalente y cada cara superior colocada en
las columnas son iguales y entre una y otra forman secuencia.
1. Antes de emprezar, las fichas se colocan boca abajo sobre la mesa y se
revuelven (barajan) para que luego, los jugadores escojan 7 fichas al azar,
según el juego tradicional. Si sólo juegan dos personas las fichas restantes,
igualmente boca abajo, se colocarán en un lateral para usarlas más tarde.
2. Empieza a jugar, el jugador que tiene el doble más grande. Y continúa el ju-
gador situado a su derecha. Esta condición puede variar según la intención
del juego.
3. En las siguientes rondas, empezará el jugador que primero logró colocar
sus 7 fichas en la ronda anterior y podrá tirar cualquier ficha, no tiene por
qué ser doble. Seguirán el juego tal como lo hicieron en la primera ronda.
4. En caso de cierre, es decir, cuando, a pesar de quedar fichas en juego en
manos de los jugadores, estos no pueden jugarlas. En este caso, ganará el
jugador cuyas fichas sumen menos puntos.
5. Normalmente se juega varias rondas. El jugador que gana una ronda, suma
los puntos de las fichas de sus adversarios y/o pareja. El primer jugador o
pareja que alcanza la puntuación acordada, gana.
Dobles o fichas
de caras iguales.
Modelo de dominó
tradicional.
Modelo de dominó como
estrategia para la ense-
ñanza de la matemática.
Fichas fraccionarias o
fichas de caras diferentes.
9 11-2 8 5-3
Observa y analiza las combinaciones que presenta el juego de dominó tradicional y algunas explicacio-
nes que pueden ayudar:
C

73. Unidad 4 - Resta54
RestemosLección 1:
(1/4~2/4)
• Realizar los cálculos del tipo D0–D0.Objetivo:
Materiales:
5 Desarrollo de clases
1. Repasar lo aprendido en
Primer Grado jugando do-
minó (Véase columnas)
* Formar grupos de 4 alumnos/
as en una mesa y entrega un
juego de dominó a cada grupo.
* Oriéntar para la colocación de
las fichas y dejar que jueguen
durante unos minutos libre-
mente.
* Motívar a participar en una
competencia de dominó con
sus compañeros y compañe-
ras ofreciendo, si es posible
una medalla al ganador.
2. Invítar a observar el dominó
que aparece en su Libro de
Estudiantes, comentar.
(M) azulejos.
(N) azulejos.
Lección 1: Restemos
Unidad 4
1 ¿Cuántos repollos quedaron en
el huerto?
40 cuarenta
Resta
2 Escriba el planteamiento de
la operación.
30 - 10
1 Calcule las siguientes restas.
(1) 40 - 20 = (2) 50 - 10 = (3) 90 - 10 = (4) 60 - 10 =
(5) 70 - 50 = (6) 80 - 60 = (7) 30 - 20 = (8) 40 - 10 =
(9) 20 - 10 = (10) 50 - 20 = (11) 60 - 30 = (12) 70 - 20 =
3 Encuentre la respuesta.
Planteamiento de la operación: 30 - 10 = 20
Respuesta: 20 repollos
A Observa y contesta.
Recordemos
Inicio
9-5 4-2
6-2
7-3
9-2
8-1
10-2
12-4
8-39-3
7-1
11-59-1
9-415-6
9-0
17-8 14-9
8-4
10-1
10-6
Habían
30 repollos
Cortó
10 repollos
20 40 80 50
20 20 10 30
10 30 30 50
(1/4~2/4)
4
77
5
6
8
5
5
4
1. Comenta la situación del
problema [A]
M: ¿Con cuál operación se pue-
de encontrar el resultado?
2. Escribir el PO. [A1]
M: ¿Cómo será el PO? Escríban-
lo en sus cuadernos.
* No es necesario resolver en
este momento.
3. Encontrar el resultado. [A2]
* Indicar que en forma indivi-
dual encuentren el resultado,
si es necesario pueden usar
los azulejos.
* Informar que cuando se usan
los azulejos o los objetos se-
miconcretos para encontrar el
resultado, sólo se representa
el minuendo, el sustraendo es
la parte que se quita.
4. Presentar lo encontrado.
M: ¿Cómo encontraron el resultado?
RP: Coloqué 3 azulejos de 10
que equivalen a los 30 repo-
llos que habían en el huerto
Continúa en la siguiente página…
[Hasta aquí 1/4]
[Desde aquí 2/4]

74. Guía para maestros/as - Matemática 20
Grado 55
Lección 1:
(3/4)
Objetivo:
Materiales:
Restemos
• Realizar los cálculos del tipo DU–D0=U.
(M) azulejos.
(N) azulejos.
1. Comentar la situación del
problema. [B]
* Orientar para que piensen
con cuál operación se puede
encontrar el resultado.
Que digan la razón de aplicar
la resta a este problema.
2. Escribir el PO. [B1]
M: ¿Cómo será el PO? Escrí-
banlo en el cuaderno.
3. Encontrar el resultado. [B2]
M: Resuelvan en forma individual,
pueden usar los azulejos.
4. Presentar lo encontrado.
M: ¿Cómo resolvieron?
RP: Coloqué 3 azulejos de 10 y 9
de 1, quité 3 de 10 y me que-
daron los 9 de 1.
Que se den cuenta que para
calcular este tipo, sólo se res-
tan las decenas y el resultado
son las unidades.
* Si no sale una buena opinión
el maestro o la maestra pue-
de inducirla.
5. Resolver los ejercicios 2 y 3 .
41cuarenta y uno
B Resuelva.
2 Calcule las siguientes restas.
3 Complete el juego de dominó.
Inicio Final
1. Hay 39 manzanas.
2. 30 manzanas son rojas.
3. ¿Cuántas manzanas verdes hay?
(1) 29 - 20 = (2) 46 - 40 = (3) 24 - 20 = (4) 67 - 60 =
(5) 99 - 90 = (6) 53 - 50 = (7) 78 - 70 = (8) 15 - 10 =
2 Encuentre la respuesta.
Planteamiento de la operación: 39 - 30 = 9
Respuesta: 9 manzanas verdes
1 Escriba el planteamiento de la operación.
39 - 30
88-40
78-7063-60
73-70
3 3
36-30
16-10
9 6 4 7
9 3 8 5
(3/4)
8
8486
… viene de la página anterior
y después quité 1 azulejo que
equivale a los 10 repollos que
se cortaron, sobró 2 azulejos
que equivalen a 20 unidades.
* Si surge la idea en los niños
y niñas de restar los números
de las decenas y agregar el
cero para encontrar el resul-
tado, hay que felicitarles y se
debe concluir de esta forma.
* Orientar que escriban la respues-
ta en el cuaderno (R: 20 repollos)
5. Resolver el ejercicio 1 .
[Hasta aquí 2/4]
[Desde aquí 3/4]

75. Unidad 4 - Resta56
1. Comentar la situación del
problema. [C]
2. Escribir el PO. [C1]
3. Encontrar el resultado. [C2]
Que se den cuenta que en
este tipo el resultado se en-
cuentra sólo copiando la
decena y restando las uni-
dades.
4. Resolver el ejercicio 3 .
42 cuarenta y dos
C ¿Cuántos peluches más que carros hay?
1 Escriba el planteamiento de la operación.
27 - 7
3 Calcule las siguientes restas.
(1) 49 - 9 = (2) 63 - 3 = (3) 84 - 4 = (4) 37 - 7 =
(5) 56 - 6 = (6) 48 - 8 = (7) 16 - 6 = (8) 35 - 5 =
María tiene 27 peluches. Alberto tiene 7 carros.
2 Encuentre la respuesta.
Planteamiento de la operación: 27 - 7 = 20
Resultado: 20 peluches
40 60 80 30
50 40 10 30
(4/4)
Lección 1:
(4/4)
Objetivo:
Materiales:
Restemos
• Realizar los cálculos del tipo DU–U=D0.
(M) azulejos.
(N) azulejos.

76. Guía para maestros/as - Matemática 20
Grado 57
Lección 2:
(1/4)
Objetivo:
Materiales:
Sigamos restando
• Resolver los cálculos operativos de DU–DU (sin y
con 0) sin reagrupar, introduciendo el algoritmo (for-
ma vertical).
1. Comentar la situación del
problema. [A]
* Orientar para que piensen
con cuál operación se puede
encontrar el resultado.
2. Escribir el PO. [A1]
M: ¿Cómo será el PO? Escríban-
lo en su cuaderno.
* Orientar sobre la forma verti-
cal de expresar el PO.
3. Indicar el proceso para ob-
tener el resultado. [A2]
M: Vamos a pensar en forma in-
dividual cómo calcular.
* Indicar que si tienen dificultad
utilicen los azulejos.
* Indicar que presenten las opi-
niones.
* Si no surge la forma vertical,
presentarla.
Que se den cuenta que se pue-
de restar por la posición, es de-
cir, unidad con unidad y decena
con decena.
4. Calcular en forma vertical.
* Aprovechando las opiniones
presentadas, explicar el pro-
ceso del cálculo vertical.
M: ¿Qué les parece ésta forma?
Que se den cuenta que la forma
vertical facilita el cálculo por la
ubicación de los números. Aun-
que pueden usar la forma hori-
zontal cuando les resulte fácil.
5. Resolver el ejercicio 1 .
* Las operaciones del (6) al (10)
son del mismo tipo pero contie-
nen “0”.
En este tipo de cálculo de la resta los niños y las niñas
pueden encontrar el resultado iniciando desde las de-
cenas o calculando mentalmente por que no se tiene
que reagrupar, es recomendable que el maestro o la maestra
aclare el proceso desde donde se empieza a restar (unidades) para
que en los cálculos siguientes no vayan a tener dificultades.
(M) azulejos.
(N) azulejos.
43cuarenta y tres
A Habían 35 guineos y se comió 21 guineos. ¿Cuántos guineos sobraron?
1 Calcule las siguientes restas.
Lección 2: Sigamos restando
Dominicana
limpia
2 Encuentre la manera de resolver.
Planteamiento de la operación: 35 - 21 = 14
Respuesta: 14 guineos
1 Colocar los números
unidad debajo de unidad,
decena debajo de decena
2 Restar las unidades:
5 - 1 = 4
3 Restar las decenas:
3 - 2 = 1
4 35 - 21 = 14
D U
3 5
2 1-
3 5
2 1-
4
3 5
2 1-
41
3 5
2 1-
41
1 Escriba el planteamiento de la operación. 35 - 21
(2) 36 - 13 = (3) 29 - 15 = (4) 23 - 11 =
(7) 27 - 17 = (8) 47 - 20 = (9) 50 - 30 =
(1) 47 - 25 =
47
25
(6) 72 - 42 =
72
42
36
13
29
15
23
11
27
17
47
20
50
30
(5) 78 - 46 =
(10) 63 - 40 =
78
46
63
40
22 23 14 12 32
23 14 12
10 27 20
22
30
32
23
(1/4)
30 10 27 20 23

77. Unidad 4 - Resta58
1. Comentar la situación del
problema. [B]
M: ¿Con cuál operación se pue-
de encontrar el resultado?
2. Escribir el PO. [B1]
M: ¿Cómo será el PO? Escríban-
lo en su cuaderno.
3. Calcular la resta. [B2]
* Indicar que resuelvan indivi-
dualmente.
* Indicar que presenten su tra-
bajo (incluyendo los errores).
* Indicar que tengan cuidado
cuando resten con “0”.
4. Resolver los ejercicios 2 y 3 .
* Los ejercicios de 3 son del
mismo tipo pero contienen “0”.
Lección 2:
(2/4)
Objetivo:
Materiales:
Sigamos restando
• Resolver los cálculos de la operación del tipo
DU–DU=U (sin y con 0) sin reagrupar.
El maestro o la maestra debe estar pendiente de los
ejercicios que contienen cero, porque los niños y las
niñas se confunden con facilidad. Algunos niños y niñas
contestan así: 24 - 22 = 02. Es importante hacerles saber que este
cero se puede eliminar siempre que esté a la izquierda y el resultado
no cambia, por lo que se debe escribir así: 24 - 22 = 2.
(M) láminas con cara de gatos.
B Hay 28 gatos de los cuáles 22 gatos son blancos.
¿Cuántos gatos negros hay?
2 Realice las siguientes restas.
3 Reste.
44 cuarenta y cuatro
D U(1)
-
3 4
3 1
D U(2)
7 8
7 5-
D U(3)
5 6
5 2-
D U(4)
4 9
4 3-
D U(5)
9 7
9 6-
(2) 48 - 48 = (3) 65 - 65 = (4) 59 - 50 =
(6) 80 - 80 = (7) 61 - 61 = (8) 34 - 30 =
2 Encuentre el resultado.
Planteamiento
de la operación: 28 - 22 = 6
Respuesta: 6 gatos negros
2 8
2 2
0 6
(1) 27 - 27 = 0
27
27
Ejemplo
0
(5) 70 - 70 =
70
70
48
48
65
60
59
50
80
80
61
61
34
30
1 Escriba el planteamiento de la operación. 28 - 22
D U
2 8
0 6
2 2
0 5 9
0 0 40
0 3 0 3 0 4 0 6 0 1
0
0 5 9
0 0 4
(2/4)

78. Guía para maestros/as - Matemática 20
Grado 59
Lección 2:
(3/4)
1. Comentar la situación del
problema. [C]
2. Escribir el PO en forma ho-
rizontal y vertical. [C1]
* Informarles que hay que tener
cuidado al colocar los números
para restar en la forma vertical.
3. Calcular resta tanto hori-
zontal como vertical. [C2]
* Indicar que presenten su traba-
jo y examinar cada caso, inclu-
yendo los cálculos erróneos.
4. Resolver los ejercicios 4 y 5 .
* El ejercicio 5 corresponde a
los tipos DU–U=D0, DU–0 y
D0–0.
* Si no hay suficiente tiempo
para desarrollar los ejercicios
en la clase se pueden dejar
de tarea.
C Habían 37 peces y pescaron 5 peces.
¿Cuántos peces quedaron en el estanque?
4 Calcule las siguientes restas.
5 Calcule las siguientes restas.
45cuarenta y cinco
2 Encuentre el resultado en forma vertical.
Planteamiento
de la operación: 37 - 5 = 32
Respuesta: 32 peces
3 7
3 2
5
(1) 44
2
(2) 83
1
(3) 57
5
(4) 34
3
(5) 69
6
(6) 92
1
(7) 56
4
(8) 25
2
D U
(1) 82 - 2 =
-
D U
(2) 43 - 3 =
-
D U
(3) 36 - 6 =
-
D U
(4) 57 - 7 =
-
(6) 19 - 0 =
19
0
(7) 20 - 0 =
20
0
(8) 70 - 0 =
70
0
1 Escriba el planteamiento de la operación. 37 - 5
D U
3 7
3 2
5
(5) 61 - 0 =
61
0
80 40 30 50
19 20 7061
8 2
8 0
2
4 3
4 0
3
3 6
3 0
6
5 7
5 0
7
42 82 52 31
63 91 52 23
19 20 70
(3/4)
61
Objetivo:
Materiales:
Sigamos restando
• Resolver los cálculos de la operación del tipo
DU–U=DU (sin y con 0).
(M) láminas.

79. Unidad 4 - Resta60
Lección 2:
(4/4)
Objetivo:
Materiales:
Sigamos restando
• Resolver problemas del tipo DU-U y DU-DU aplican-
do el algoritmo de la resta.
1. Comentar la situación del
problema. [D]
2. Presentar la solución.
3. Confirmar el proceso.
M: ¿Qué pasos siguieron para
resolver el problema?
RP: 1) Buscar las palabras cla-
ves.
2) Pensar con qué operación
se puede resolver.
3) Escribir el PO.
4) Desarrollar el cálculo y en-
contrar el resultado.
5) Escribir la respuesta de
acuerdo a la pregunta.
4. Resolver el ejercicio 6 .
D Omery tiene 27 barquillas y Carlos tiene 14 fresas.
¿Cuántas barquillas hay más que fresas?
6 Resuelva los siguientes problemas.
Planteamiento
de la operación:
Respuesta: __________________________
Planteamiento
de la operación:
Respuesta: __________________________
Planteamiento
de la operación:
Respuesta: __________________________
46 cuarenta y seis
Mmmm.
(1) Mi mamá tenía 48 gallinas y vendió 15 gallinas.
¿Cuántas gallinas le quedaron?
En segundo grado hay 45 alumnos y hoy faltaron
3 alumnos. ¿Cuántos alumnos llegaron hoy?
(3) Rita hizo 29 pasteles y vendió 7 pasteles.
¿Cuántos pasteles le quedaron?
Omery Carlos
__________________________
__________________________
Cálculo
Cálculo
Cálculo
__________________________
27
14
13
2 Encuentre el resultado.
3 Invente un problema usando 27 - 4.
Planteamiento
de la operación: 27 - 14 = 13
Respuesta: 13 barquillas
1 Escriba el planteamiento de la operación. 27 - 14
(2)
(4/4)
48 - 15 = 33
33 gallinas
45 - 3 = 42
42 alumnos
48
15
33
45
3
42
29
7
22
29 - 7 = 22
22 pasteles

80. Guía para maestros/as - Matemática 20
Grado 61
• Confirmar lo aprendido en la lección 2.
• Reforzar el cálculo de operaciones del tipo DU - DU
(sin y con cero).
1 Ejercicios del cálculo verti-
cal sin reagrupar.
2 Ejercicios para la confir-
mación del valor posicional.
3 Problemas de aplicación.
4 Construcción de los pro-
blemas de la resta.
2 Resuelva cambiando a la forma vertical.
3 Desarrolle los siguientes problemas.
47cuarenta y siete
(1) En el patio estaban jugando 38 niños y luego se fueron 12 niños.
¿Cuántos niños quedaron jugando en el patio?
(2) Hay 77 guineos y 40 piñas. ¿Cuántos guineos hay más
que piñas?
1 Calcule las siguientes restas.
(2) (3) (4)(1)
(5)
35
12
54
3
(6)
53
20
67
7
(7)
69
69
24
0
(8)
90
60
38
34
(2) 79 - 36 = (3) 63 - 40 = (4) 80 - 70 =(1) 43 - 13 =
(5) 37 - 3 =
Cálculo
Planteamiento de la operación:___________________
Respuesta:___________________
4 Invente problemas con los siguientes planteamientos de la operación y resuelva.
(1) 68 - 21 = (2) 50 - 20 = (3) 47 - 27 =
(5) 86 - 6 = (6) 10 - 0 =
(6) 98 - 6 = (7) 45 - 5 = (8) 72 - 0 =
Hay 47 rosas entre rojas y blancas. Si 5 rosas son blancas,
¿cuántas rosas rojas hay?
(3)
(4) 79 - 5 =
Planteamiento de la operación:___________________
Respuesta:___________________
Cálculo
Planteamiento de la operación:___________________
Respuesta:___________________
Cálculo
Ejercicios (1)
43 23 1030
34
47 30 20
80 10
92 40 72
74
42
47
5
37
77
40
26
38
12
23
51
33
60
0
24
30
4
43
79
36
23
63
40
10
80
70
30
43
13
92
98
6
40
45
5
72
72
0
34
37
3
47 - 5 = 42
42 rosas rojas
Se omite la solución
(1/1)
77 - 40 = 37
37 guineos
38 - 12 = 26
26 niños
Unidad 4:
(1/1)
Objetivo:
Materiales:
Ejercicios (1)

81. Unidad 4 - Resta62
Lección 3:
(1/4)
Objetivo:
Materiales:
Restemos reagrupando
• Resolver los cálculos operativos de
DU – DU = DU reagrupando.
(M) azulejos.
(N) azulejos.
1. Comentar la situación del
problema. [A]
M: ¿Cómo se puede resolver el
problema?
2. Escribir el PO. [A1]
* Indicar a los niños y niñas que
escriban el PO.
3. Encontrar la manera de re-
solver. [A2]
* Indicar que resuelvan individual-
mente utilizando los azulejos.
* Orientar a los niños y a las ni-
ñas que tienen dificultad.
RP: No se puede restar 7 de 2.
M: Entonces, piensen cómo se
puede restar.
RP: Ya recordé, en 1er grado aprendí
esta manera.
* Indicar que presenten sus
ideas.
* Si no sale la respuesta espe-
rada el maestro o la maestra
puede inducirla.
Que capten que si no se puede
restar en una posición se utiliza-
rá un grupo de 10 de la posición
inmediata superior (de la izquier-
da) para tener la cantidad sufi-
ciente y poder restar.
4. Pensar la forma de hacer el
cálculo vertical con los nú-
meros.
* Escribir “32–17” en forma verti-
cal en la pizarra.
* Indicar que hagan el cálculo si-
guiendo el proceso que realiza-
ron con los azulejos.
* Explicar la importancia de es-
cribir los números auxiliares y
tachar los números.
* Concluir aclarando los pasos que
se siguen para calcular la resta
reagrupando.
* Indicar que escriban la respuesta
(R: 15 piñas verdes).
5. Resolver el ejercicio 1 .
Es recomendable que los niños y las niñas escriban los
números reagrupados y que tachen los números que se
sustituyeron para evitar errores en el cálculo.
48 cuarenta y ocho
A Hay 32 piñas verdes y maduras, 17 están maduras.
¿Cuántas piñas verdes hay?
Lección 3: Restemos reagrupando
1 Escriba el planteamiento de la operación.
2 Encuentre la manera de resolver.
32 - 17
D U
3 2
1 7
1 Haga las siguientes restas.
Planteamiento
de la operación: 32 - 17 = 15
Respuesta: 15 piñas verdes
_
3 2
1 7
2
_
3 2
1 7
2
_
5
3 2
1 7
2
_
1 5
1
2
1 7
2
_
1 5
1
D U(1)
-
7 2
3 5
D U(2)
3 1
-
D U(3)
5 3
2 6-
D U(4)
4 7
1 8-1 7
1 Colocar los números ordenadamente
(en cada posición).
2 Restar las unidades:
12 - 7 = 5
No se puede restar 7 de 2.
Pedir prestada 1 decena.
El 3 de las decenas ya es 2
porque prestó 1 a las unidades.
(tachar 3 y escribir 2)
3 Restar las decenas:
como ya prestó 1, quedó 2.
2 - 1 = 1
4 32 - 17 = 15
1
1
Dominicana
limpia
3 7
1
1 4
1
2 7
1
2 9
1
6
(1/4)
2 4 3

82. Guía para maestros/as - Matemática 20
Grado 63
Lección 3:
(2/4)
Objetivo:
Materiales:
Restemos reagrupando
• Resolver los cálculos operativos de
D0 – DU = DU reagrupando.
1. Comentar la situación del
problema. [B]
M: ¿Cómo se puede resolver el
problema?
2. Escribir el PO. [B1]
M: ¿Cómo será el PO? Escríban-
lo en sus cuadernos.
3. Calcular. [B2]
* Indicar que resuelvan indivi-
dualmente.
* Informar que no es necesario la
tabla de valores ni el uso de los
azulejos. Estos recursos deben
usarlos solamente los niños y
niñas que tengan dificultad.
* Garantizar el tiempo suficien-
te para que todos terminen.
4. Explicar la manera de resolver.
* Indicar que presenten su tra-
bajo en la pizarra y que expli-
quen paso a paso.
* Confirmar que se escriben los
números reagrupados, arriba de
las unidades y decenas del mi-
nuendo, y se tacha el número de
la decena.
* Realizar otros ejercicios.
5. Resolver los ejercicios 2 y 3 .
(M) materiales del medio.
B Habían 30 zanahorias y se comió 18.
¿Cuántas zanahorias quedaron?
1 Escriba el planteamiento de la operación.
2 Encuentre el resultado en forma vertical.
30 - 18
2 Calcule las siguientes restas.
3 Resuelva cambiando el planteamiento de la operación a la forma vertical.
49cuarenta y nueve
(1) 7 0
1 6
(2) 5 0
2 7
(3) 6 0
3 9
(4) 4 0
1 8
(1) 90 - 62 = (2) 80 - 25 = (3) 70 - 26 =
(4) 60 - 39 = (5) 50 - 14 = (6) 40 - 23 =
Planteamiento
de la operación: 30 - 18 = 12
Respuesta: 12 zanahorias
D U
3 0
1 2
1 8
2
1
3 0
1 8
1 2
2
1
Cuando se pasa 1
decena a las unidades
es igual a...
28 55 44
21 36 17
1 1 1 1
6 4 5 3
5 4 2 3 2 1 2 2
9 0
6 2
2 8
8
1 8 0
2 5
5 5
7
1 7 0
2 6
4 4
6
1
4 0
2 3
1 7
3
15 0
1 4
3 6
4
16 0
3 9
2 1
5
1
(2/4)

83. Unidad 4 - Resta64
Lección 3:
(3/4)
Objetivo:
Materiales:
Restemos reagrupando
• Resolver los cálculos operativos de DU–DU=U y D0–
DU=U reagrupando.
1. Comentar la situación del
problema. [C]
M: ¿Cómo se puede resolver el
problema?
2. Escribir el PO. [C1]
3. Calcular. [C2]
Que se den cuenta que de la
diferencia entre los ejercicios
anteriores y éste, consiste en
que en las decenas no que-
dan cantidades.
4. Explicar la manera de resol-
ver.
* Indicar que presenten su tra-
bajo en la pizarra y que expli-
quen paso a paso.
* Confirmar que se escriben los
números reagrupados, arriba de
las unidades y decenas y que se
tacha el número de la decena.
* Indicar que no es necesario es-
cribir el 0 en la respuesta, sin
embargo en la primera etapa
(cálculo) se puede aceptar su
escritura y tacharlo.
5. Resolver los ejercicios 4 y
5 .
* El ejercicio 5 corresponde al
tipo D0–DU=U.
C Hay 37 pájaros de los cuales 28 son amarillos.
¿Cuántos pájaros azules hay?
1 Escriba el planteamiento de la operación.
2 Encuentre el resultado.
37 - 28
4 Calcule las siguientes restas.
5 Calcule las siguientes restas.
50 cincuenta
(1) 45 - 37 = (2) 52 - 49 = (3) 45 - 36 = (4) 23 - 15 =
Planteamiento
de la operación: 37 - 28 = 9
Respuesta: 9 pájaros azules
D U
3 7
0 9
2 8
2
1
3 7
2 8
0 9
2
1
4 5
3 7
5 2
4 9
4 5
3 6
2 3
1 5
(1) 20 - 14 =
(5) 70 - 62 =
(2) 50 - 43 =
(6) 90 - 89 =
(3) 60 - 58 =
(7) 30 - 21 =
(4) 80 - 75 =
(8) 40 - 36 =
8 3 9 8
6
8
7
1
2
9
5
4
3 4 3 1
1 1 1 1
(3/4)
0 8 0 3 0 9 0 8
2 0
1 4
6
1
1
7 0
6 2
8
6
1 9 0
8 9
1
8
1
5 0
4 3
7
4
1
3 0
2 1
9
2
1
6 0
5 8
2
5
1
4 0
3 6
4
3
1
8 0
7 5
5
7
1

84. Guía para maestros/as - Matemática 20
Grado 65
Lección 3:
(4/4)
Objetivo:
Materiales:
Restemos reagrupando
• Resolver cálculos operativos del tipo DU–U=DU y
D0–U=DU reagrupando.
1. Comentar la situación del
problema. [D]
M: ¿Cómo se puede resolver el
problema?
2. Escribir el PO. [D1]
* Indicar a los niños y a las ni-
ñas que escriban el PO.
3. Calcular. [D2]
* Indicar que primero resuelvan in-
dividualmente en sus cuadernos.
* Orientar a los niños y niñas
que tienen dificultad que el
cálculo es parecido a los que
aprendieron anteriormente.
* Indicar que coloquen los núme-
ros de las unidades y las dece-
nas en la misma columna.
Que se den cuenta que en la
posición de las decenas, en
el sustraendo no hay ningún
dígito, por lo tanto la cantidad
que queda en el minuendo
sólo se baja y es la respuesta
de las decenas.
4. Resolver los ejercicios 6 y 7 .
* El ejercicio 7 corresponde al
tipo de D0–U=DU.
* Indicar que resuelvan sólo con
los números y en caso de que
haya dificultad pueden usar los
azulejos y/o auxiliarse de la ta-
bla de valores.
Es recomendable dar a los niños y a las niñas suficien-
te tiempo hasta que dominen el método de la resta re-
agrupando usando los números de dos cifras, para que
cuando tengan que operar la resta con los números de tres o
más cifras no tengan mucha dificultad.
D Don Pedro tenía 46 huevos y regaló 8.
¿Cuántos huevos le quedaron?
1 Escriba el planteamiento de la operación.
2 Encuentre la respuesta.
46 - 8
6 Calcule las siguientes restas.
7 Calcule las siguientes restas.
51cincuenta y uno
(2) 4 3
7
(3) 5 1
5
(1) 3 8
9
(4) 6 2
7
(5) 9 6
8
(6) 7 5
9
(2) 6 0
6
(6) 9 0
4
(3) 7 0
9
(7) 3 0
5
(1) 4 0
8
3 2
1
3
(5) 8 0
3
(4) 5 0
2
(8) 2 0
7
Huevos
D U
4 6
3 8
8
3
1
4 6
8
3 8
3
1
Planteamiento
de la operación: 46 - 8 = 38
Respuesta: 38 huevos
2 3 4
5 8 6
5 6 4
7 8 2 1
1 1 1
1 1 1
1 1 1
1 1 1 1
(4/4)
2 9 3 6 4 6
5 5 8 8 6 6
5 4 6 1 4 8
7 7 8 6 2 5 1 3

85. Unidad 4 - Resta66
Los ejercicios tratan sobre:
1 Cálculo vertical DU – DU
reagrupando.
2 Cálculo vertical D0 – DU
y DU – DU = U reagrupando.
3 Ejercicios para la confir-
mación del valor posicional.
Continúa en la siguiente página…
52 cincuenta y dos
1 Calcule las siguientes restas.
2 Calcule las siguientes restas.
3 Resuelva.
(1) 3 1
1 9
(1) 47 - 19 =
(1) 8 0
2 4
(2) 6 0
1 8
(4) 6 2
5 9
(5) 7 6
6 8
(2) 6 4
2 8
(4) 8 2
1 7
(5) 8 8
2 9
(2) 50 - 25 = (3) 38 - 29 =
(3) 7 0
6
(3) 9 3
4 6
(4) 53 - 7 = (5) 30 - 3 =
Ejercicios (2)
28 25 9
46 27
1
1 1
1 1
1
1 1
1
1
2
7 5
5 6
5
7 7
6
8
(1/1)
1 2
5 6 4 2
3 8
3 6
6 5 5 9
4 7
1 9
2 8
3
1 5 0
2 5
2 5
4
1
6 4
4 7
3 8
2 9
9
2
1
5 3
7
4 6
4
1 3 0
3
2 7
2
1
• Resolver cálculos operativos del tipo DU–U=DU y
D0–U=DU reagrupando.
Unidad 4:
(1/1)
Objetivo:
Materiales:
Ejercicios (2)

86. Guía para maestros/as - Matemática 20
Grado 67
Planteamiento de la operación:___________________
Planteamiento de la operación:___________________
Respuesta:___________________
Respuesta:___________________
53cincuenta y tres
4 Desarrolle los siguientes problemas.
Rosita tiene 24 libros y su hermano tiene 19 libros.
¿Cuántos libros más tiene Rosita que su hermano?
El papá de Juan tenía 64 vacas y vendió 35 vacas.
¿Cuántas vacas le quedaron?
En el jardín hay 70 flores rojas y blancas, 36 son rojas.
¿Cuántas flores blancas hay en el jardín?
(1)
Cálculo
Cálculo
Planteamiento de la operación:___________________
Respuesta:___________________
Cálculo
(2)
(3)
5 Invente problemas con los siguientes planteamientos de la operación.
(1) 63 - 46 =
(2) 70 - 54 =
(3) 42 - 38 =
(4) 26 - 9 =
17
16
4
17
64 - 35 = 29
29 vacas
6 4
3 5
2 9
5
1
24 - 19 = 5
5 libros
2 4
1 9
5
1
1
70 - 36 = 34
34 flores blancas
7 0
3 6
3 4
6
1
Se omite la solución
(1/1)
[Continuación]
… viene de la página anterior
4 Problemas de aplicación.
5 Construcción de problemas.
Unidad 4:
(1/1)
Ejercicios (2)

87. Unidad 4 - Resta68
• Confirmar lo aprendido en toda la unidad.
Los ejercicios tratan sobre:
1 Ejercicios de todos los ti-
pos de cálculos de resta sin
reagrupar y reagrupando.
2 Problemas de aplicación.
Continúa en la siguiente página…
1 Calcule las siguientes restas.
Ejercicios (3)
54 cincuenta y cuatro
2 Desarrolle los siguientes problemas.
En la laguna habían 23 patos, se fueron 19 patos.
¿Cuántos patos quedaron?
___________________________
___________________________
Cálculo
(1)
En la sección "A" de segundo grado hay 26 niñas y 15 niños.
¿Cuántas niñas más que niños hay?
(2)
___________________________
___________________________
Cálculo
(2) 54 - 19 =
(6) 46 - 38 =
(3) 40 - 20 =
(7) 80 - 3 =
(1) 67 - 24 =
(5) 29 - 20 =
(4) 80 - 34 =
(8) 34 - 9 =
(10) 62 - 46 = (11) 30 - 7 =(9) 98 - 24 = (12) 42 - 39 =
Planteamiento
de la operación:
Respuesta:
Planteamiento
de la operación:
Respuesta:
35
8
20
77
43
9
46
25
16 2374 3
4 7
5 2 3
(1/1)
23 - 19 = 4
4 patos
2 3
1 9
4
1
1
26 - 15 = 11
11 niñas
2 6
1 5
1 1
5 4
1 9
4 6
3 8
4 0
2 0
8 0
3
6 7
2 4
4 3
2 9
2 0
8 0
3 4
3 4
9
3 5
1
2 0 4 6
1
9 8
3
1
7 7
7
1
2 5
2
1
6 2
4 6
3 0
7
9 8
2 4
4 2
3 9
7 4 1 6
1
2 3
1
3
1
Unidad 4:
(1/1)
Objetivo:
Materiales:
Ejercicios (3)

88. Guía para maestros/as - Matemática 20
Grado 69
4 Coloca los números que faltan en el juego de dominó.
Inicio
Final
60-58
6-5
22-20
14-12
36-11
22-1724-20 6-1
10-6
45-38
20-711-5
33-21
31-19
60-48
24-19
53-48
34-31 73-25
53-50
40-2080-60
55cincuenta y cinco
3 Invente problemas y resuélvalos.
(1)
(2)
(3)
(4)
30 - 10 =
24 - 12 =
43 - 18 =
74 - 9 =
Hay 35 niños y 8 pasteles.
¿Cuántos niños hay más que pasteles?
(3)
___________________________
___________________________
Cálculo
Planteamiento
de la operación:
Respuesta:
20
12
25
65
2
25
13
7
6
12
48
20
35 - 8 = 27
27 niños
3 5
8
2 7
2
1
(1/1)
Se omite la solución
… viene de la página anterior
3 Elaboración de problemas
de la resta.
4 Juego de dominó.[Continuación]
Unidad 4:
(1/1)
Ejercicios (3)

89. Unidad 5 - Suma y resta combinadas70
• Resuelven situaciones de la vida cotidiana que implican adiciones y sustracciones combinadas.
Expectativas de logro1
Números hasta 999 Números hasta 9,999 Números hasta 1,000,000Números hasta 9
Relación y desarrollo2
Adición y sustracción
Adición y sustracción con
números menor o igual
que 1,000,000
Aproximación de adición y
sustracción
Números hasta 19
Suma y resta combinada
• Suma con tres suman-
dos.
• Resta con tres sus-
traendos.
• Suma y resta combina-
das.
Operaciones combinadas
• Orden de cálculo.
• Uso de paréntesis.
• Propiedad asociativa de
la adición.
• Propiedad asociativa de
la multiplicación.
Resta (2)
Sustracción cuyo minuen-
do sea menor o igual que
18 y mayor al sustraendo
Números hasta 99
Suma (1)
Adición cuyo total sea
menor o igual que 9
Suma
Adición cuyos sumandos
sean menor que 100
Adición
Adición con sumandos
menores que 1,000
Suma (2)
Adición cuyo total sea
menor que 18
Sustracción
Sustracción con minuen-
dos menores que 1,000
Resta
Sustracción cuyo minuen-
do sea menor que 100
Resta (1)
Sustracción cuyo minuen-
do sea menor o igual
que 9 y mayor o igual al
sustraendo
Suma y resta combinadas (6 horas)Unidad
55

90. Guía para maestros/as- Matemática 20
Grado 71
Puntos de lección
• Lección 1: Sumemos y restemos
Para la resolución de problemas, es funda-
mental captar cuál es la operación que se
debe utilizar. Si los niños y niñas no logran
hacer esa distinción, aunque sepan sumar y
restar, no podrán aplicar lo aprendido para re-
solver situaciones de la vida diaria. Por otra
parte, mediante la expresión de la operación
planteada se conduce al desarrollo de un pen-
samiento matemático más elevado, por lo que
hay que darle importancia, no sólo al nivel de
cálculo para resolver el problema donde apa-
recen tres números sino que también al pro-
ceso del planteamiento de la operación.
En esta unidad vamos a desarrollar en los
niños y las niñas la habilidad para identificar
la operación adecuada para plantear una si-
tuación dada y hacer los cálculos de sumas y
restas sucesivas y combinadas correctamen-
te. Al hacer los cálculos es importante que no-
ten la diferencia entre la suma y la resta. En
el caso de la suma, como es una operación
asociativa, no importa cuales números sume-
mos primero. En el caso de la resta sucesiva
el orden es de izquierda a derecha. Se deben
analizar varios ejemplos para que capten bien
esa situación. En este momento no hay que
mencionar la propiedad asociativa, solo que
capten la idea.
4
1/4~2/4 • Planteamiento de la operación y cálculo de sumas
sucesivas
3 Plan de estudio (6 horas)
1. Sumemos y restemos
(4 horas)
3/4 • Planteamiento de la operación y cálculo de restas
sucesivas
4/4 • Planteamiento de la operación y cálculo de sumas y
restas combinadas
1/2~2/2 Ejercicios
(2 horas)
• Ejercicios

91. Unidad 5 - Suma y resta combinadas72
Sumemos y restemosLección 1:
(1/4~2/4)
• Resolver situaciones utilizando el planteamiento y
cálculo de sumas sucesivas.
Objetivo:
Materiales:
5 Desarrollo de
clases
1. Comentar la situación del
problema. [A]
M: ¿Con cuál operación se en-
cuentra el resultado?
2. Escribir el Planteamiento
de la Operación. [A1]
M: ¿Cómo será el Planteamiento
de la Operación? Escríbanlo
en sus cuadernos.
3. Encontrar la manera de cal�
cular. [A2]
M: ¿Cómo encontraron el resul-
tado? ¿Cómo hicieron?
* Pedir que presenten sus opi-
niones en la pizarra.
RP: (A) 5 + 6 = 11, 11 + 4 = 15
(B) 11 + 4 = 15
(C) 5 + 6 + 4 = 15
* Analizar cada Planteamiento de
la Operación conjuntamente y
concluir que el (C) tiene mayor
ventaja porque se puede repre-
sentar la suma sucesiva en sólo
un planteamiento.
4. Confirmar la diferencia en la
forma de cálculo de Dilenia
y Paola .
* (Escribir en la pizarra el mismo
contenido del LE sin escribir los
números en el cuadro) e indicar
a los niños y niñas que lo re-
suelvan llenando los espacios
en blanco y siguiendo el proce-
dimiento empleado por Dilenia
y luego por Paola.
Que se den cuenta que aunque
se haya seguido un proceso di-
ferente el resultado es el mismo.
Continúa en la siguiente página…
Lección 1: Sumemos y restemos
Unidad 5
A Observe el dibujo y diga, ¿cuántos niños y niñas hay en total?
56 cincuenta y seis
Suma y resta combinadas
1 Escriba el planteamiento de la operación:
2 Encuentre la manera de resolver.
5 + 6 + 4
3
5 + 6 + 4 = 15
11 + 4
15
1
2
3
+
Voy a sumar primero
los niños y niñas que están
jugando y luego las niñas que
están llegando
Yo voy a sumar
primero las niñas que
están jugando y las que están
llegando y luego los niños
5 + 6 + 4 = 15
5 + 10
15
1
2
3
Dilenia Paola
Planteamiento
de la operación: 5 + 6 + 4 = ___
Respuesta: niños y niñas
Planteamiento
de la operación: 5 +6 + 4 = ___
1 Haga las siguientes sumas sucesivas.
2 + 8 + 4 = 5 + 3 + 7 =(1) (2) 7 + 1 + 9 =(3)
Respuesta: niños y niñas
Para calcular sumas sucesivas se puede hacer en
cualquier orden y el resultado es el mismo.
15
(1/4~2/4)
15
14 15 17
1515

92. Guía para maestros/as- Matemática 20
Grado 73
Lección 1:
(1/2)
Sumemos y restemos
[Continuación]
… viene de la página anterior
* Confirmar que para calcular
sumas sucesivas se puede
hacer en cualquier orden.
* Resolver otros ejemplos para
que se entienda bien el proceso.
5. Resolver el ejercicio 1 .
6. Repasar la clase anterior:
* Presentar una situación donde
haya que plantear una suma
sucesiva y recordar el proceso
que se sigue para el cálculo.
7. Resolver los ejercicios 2 y 3 .
[Hasta aquí 1/4]
[Desde aquí 2/4]
3 Resuelva los siguientes problemas.
(1) Mi mamá tenía 7 mangos, compró 6 mangos
en el mercado y su vecino le regaló 5 mangos más.
¿Cuántos mangos tiene ahora mi mamá?
Planteamiento de la operación: ________________
Respuesta: ___ mangos.
Cálculo
2 Calcule las siguientes sumas.
(2) Andrea tiene 3 lápices rojos, 5 lápices verdes
y 9 lápices azules.¿Cuántos lápices tiene
Andrea en total?
Planteamiento de la operación: ________________
Respuesta: ___ lápices.
57cincuenta y siete
(3) Andrea tiene 21 pesos, su madre le regaló 16 pesos
y su padre le regaló 24 pesos. ¿Cuántos pesos tiene
Andrea en total?
Planteamiento de la operación: ________________
Respuesta: ___ pesos.
9 + 2 + 8 = 4 + 6 + 8 = 4 + 7 + 2 =(1) (2) (3)
5 + 5 + 8 = 3 + 2 + 8 = 7 + 5 + 3 =(4) (5) (6)
13 + 40 + 27 = 21 + 39 + 7 = 8 + 14 + 36 =(7) (8) (9)
Cálculo
Cálculo
7 + 6 + 5 = 18
18
19 18
18
80
13
67
13
15
58
7 + 6 + 5 = 18
13 + 5
18
3 + 5 + 9 = 17
8 + 9
17
3 + 5 + 9 = 17
17
21 + 16 + 24 = 61
37 + 24
61
21 + 16 + 24 = 61
61

93. Unidad 5 - Suma y resta combinadas74
Lección 1:
(3/4)
Sumemos y restemos1. ������������������������������Comentar la situación del pro�
blema. [B]
M: ¿Con cuál operación se encuentra
el resultado?
Que capten que se tiene que en-
contrar la cantidad que queda.
2. Escribir el Planteamiento
de la Operación. [B1]
M: ¿Cómo será el Planteamiento
de la Operación? Escríbanlo
en sus cuadernos.
* Indicar que utilicen un sólo Plan-
teamiento de la Operación para
expresar la resta sucesiva.
3. Encontrar la manera de cal�
cular. [B2]
M: ¿Cómo encontraron el resul-
tado? ¿Cómo hicieron?
* Pedir que presenten en la pi-
zarra lo que hicieron.
4. Confirmar la forma del cálculo.
* Escribir en la pizarra el mismo
contenido del LE sin los núme-
ros en el cuadro e indicar a los
niños y niñas que lo resuelvan
llenando los espacios en blanco.
* Confirmar que el orden del cál-
culo es de izquierda a derecha.
* Resolver otros ejemplos para
entender bien el proceso.
5. Resolver los ejercicios 4 ,
5 y 6 .
* Si no hay tiempo suficiente
pueden dejar alguno de tarea
para la casa.
• Resolver situaciones utilizando el planteamiento y
cálculo de restas sucesivas.
Objetivo:
Materiales:
B Observe el dibujo y diga, ¿cuántos patos quedaron?
4 Calcule las siguientes
restas sucesivas.
1 Escriba el planteamiento de la operación:
2 Encuentre la manera de resolver.
14 - 3 - 2
Habían 14 patos.
Primero se fueron 3 patos.
Después se fueron 2 patos.
14 - 3 - 2 = 9
11 - 2
9
Planteamiento de la operación: 14 - 3 - 2 = ___
Respuesta: Quedaron ___ patos
1
2
3
58 cincuenta y ocho
6 Resuelva el siguiente problema.
1
2
3
Para calcular restas
sucesivas se hace de
izquierda a derecha.
Restar 14 - 3 = 11
Restar 11 - 2 = 9
14 - 3 - 2 = 9
14 - 9 - 2 =(1)
12 - 3 - 5 =(2)
5 Reste haciendo el proceso.
16 - 5 - 3 =(1) 14 - 9 - 2 =(2)
73 - 26 - 12 =(3)
Cálculo
Planteamiento de la operación: ______________
(1)
Respuesta: ___ caramelos.
Susana tenía 11 caramelos. En la calle perdió 4
caramelos y luego su hermana le comió 5 caramelos.
¿Cuántos caramelos le quedaron a Susana?
9
9
(3/4)
5 - 2
3
3
9 - 5
4
4
11 - 3
8
8
5 - 2
3
3
47 - 12
35
35
11 - 4 - 5 = 2
7 - 5
2
11 - 4 - 5 = 2
2

94. Guía para maestros/as- Matemática 20
Grado 75
Sumemos y restemosLección 1:
(4/4)
Objetivo:
Materiales:
1. Comentar la situación del pro�
blema. [C]
* Orientar para que piensen de
qué manera se puede encon-
trar el resultado.
Que capten que se tiene que
encontrar la cantidad que fi-
nalmente quedan.
2. Escribir el PO. [C1]
M: ¿CómoseráelPOenestecaso?
Escríbanlo en sus cuadernos.
* indicar que apliquen lo apren-
dido en la clase anterior.
3. Encontrar la manera de cal�
cular. [C2]
M: ¿Cómo encontraron el resul-
tado? ¿Cómo hicieron?
RP: Utilicé la forma del cálculo,
paso a paso de la misma ma-
nera que la clase anterior.
* Si hay niños y niñas que se
desorientan al sumar y restar
con los cambios en la situación
del problema, se puede utilizar
los materiales concretos o se-
miconcretos para encontrar la
respuesta, manejándolos de
manera que corresponda con
el desarrollo vertical que escri-
ben en sus cuadernos.
4. Confirmar la forma del cálculo.
* Designar a algunos niños y
niñas para que resuelvan el
problema en la pizarra.
* Confirmar que también en el
caso de operaciones combina-
das de suma y resta el orden
del cálculo es de izquierda a
derecha.
5. Resolver los ejercicios 7 ,
8 y 9 .
* Si no hay tiempo suficiente se
puede dejar alguno de tarea
para la casa.
• Resolver situaciones utilizando el planteamiento y
cálculo de sumas y restas combinadas.
C ¿Cuántas aves quedaron al final en la casita?
Habían 6 aves.
Llegaron 5 aves.
Se fueron 4 aves.
59cincuenta y nueve
7 Calcule las siguientes operaciones.
1 Escriba el planteamiento de la operación:
2 Encuentre la manera de resolver.
6 + 5 - 4
6 + 5 - 4 = 7
11 - 4
7
Planteamiento de la operación: 6 + 5 - 4 = ___
Respuesta: Quedaron ___ aves
1
2
3
9 Resuelva el siguiente problema.
1
2
3
Para calcular sumas y restas
(restas y sumas) combinadas
se hace de izquierda a derecha.
Sumar 6 + 5 = 11
Restar 11 - 4 = 7
6 + 5 - 4 = 7
12 + 3 - 6 =(1)
-
17 - 8 + 5 =(2)
+
36 + 17 - 28 =(3)
8 Calcule haciendo el proceso.
11 - 4 + 2 =(2)6 + 7 - 2 =(1)
5 + 9 - 8 =(3) 49 - 26 + 18 =(4)
Cálculo
Planteamiento de la operación: ______________
(1)
Respuesta: ___ pesos.
Sandra tiene 9 pesos y su madre le regala
4 pesos más, luego ella gasta 5 pesos.
¿Cuántos pesos le quedaron a Sandra?
(4/4)
7
7
615
9
9
9 5
14
14
53 - 28
25
25
7 + 2
9
9
13 - 2
11
11
14 - 8
6
6
23 + 18
41
41
9 + 4 - 5 = 8
13 - 5
2
9 + 4 - 5 = 8
8

95. Unidad 5 - Suma y resta combinadas76
Unidad 5:
(1/2~2/2)
Objetivo:
Materiales:
Ejercicios
• Confirmar lo aprendido en toda la unidad.
Los ejercicios tratan sobre:
1 Cálculos de sumas y res-
tas sucesivas
2 Cálculos de sumas y res-
tas combinadas
3 Problemas de aplicación
4 Construcción de problemas Ejercicios
1 Calcule las siguientes sumas y restas sucesivas.
2 Calcule las siguientes operaciones combinadas.
3 Res3 Resuelva los siguientes problemas.
4 Invente problemas con los siguientes planteamientos y resuélvalos.
60 sesenta
(1) 6 + 3 - 2 (2) 5 - 2 + 4 (3) 9 + 2 - 3 (4) 6 - 4 + 7
8 + 3 + 4 =(1) 9 - 2 - 2 =(2) 9 + 4 + 5 =(3)
7 - 1 - 3 =(4) 3 + 7 + 4 =(5) 8 - 5 - 1 =(6)
9 + 8 - 5 =(1) 8 - 4 + 6 =(2) 8 + 9 - 9 =(3)
7 - 5 + 2 =(4) 8 + 5 - 7 =(5) 8 - 5 + 1 =(6)
Cálculo
Planteamiento de la operación: ______________
(1)
Respuesta: ___ niñas.
En la cancha están jugando 8 niñas, después
llegaron 3 niñas y luego 5 niñas más.
¿Cuántas niñas están jugando ahora en la cancha?
Cálculo
Planteamiento de la operación: ______________
(2)
Respuesta: ___ piñatas.
María tenía 16 piñatas. El lunes vendió 4 piñatas
y el martes vendió 6 piñatas.
¿Cuántas piñatas le quedaron a María?
Cálculo
Planteamiento de la operación: ______________
(3)
Respuesta: ___ caballos.
En una finca habían 9 caballos. Vendieron 5 caballos
y después compraron 6 caballos.
¿Cuántos caballos hay ahora?
8 + 3 + 5 = 16
11 + 5
16
16 - 4 - 6 = 6
12 - 6
6
9 - 5 + 6 = 10
4 + 6
10
Se omite la solución
(1/2~2/2)
15 5 18
3 14 2
12 10 8
4 6 4
8 + 3 + 5 = 16
16
16 - 4 - 6 = 6
6
9 - 5 + 6 = 10
10
[Hasta aquí 1/2]

96. Guía para maestros/as- Matemática 20
Grado 77
Unidad 5:
(1/2~2/2)
Ejercicios
[Continuación]
Los ejercicios tratan sobre:
5 Cálculos de sumas y res-
tas sucesivas
6 Cálculos de sumas y res-
tas combinadas
7 Problemas de aplicación
5 Calcule las siguientes sumas y restas sucesivas.
6 Calcule las siguientes operaciones combinadas.
3 Res7 Resuelva los siguientes problemas.
18 + 33 + 44 =(1) 69 - 42 - 27 =(2) 19 + 47 + 5 =(3)
77 - 11 - 33 =(4) 30 + 7 + 41 =(5) 38 - 25 - 10 =(6)
39 + 8 - 25 =(1) 18 - 14 + 16 =(2) 27 + 9 - 19 =(3)
37 - 15 + 52 =(4) 63 + 20 - 47 =(5) 17 - 5 - 9 =(6)
Cálculo
Plateamiento de la operación: __________________
(1)
Respuesta: ____ pesos.
Luis vende periódicos, el lunes se ganó 38 pesos.
el martes ganó 35 pesos y el miércoles ganó 24 pesos.
¿Cuántos pesos ganó en total los tres días?
Cálculo
Plateamiento de la operación: __________________
(2)
Respuesta: ____ pollitos.
Había 27 pollitos en una granja, se murieron 14 pollitos
y luego nacieron 23, ¿Cuántos pollitos hay ahora en la
granja?
Cálculo
Plateamiento de la operación: __________________
(3)
Respuesta: ____ pesos.
Ana tiene 80 pesos, si gasta 35 pesos y luego gasta
30 pesos más, ¿cuántos pesos le quedan?
61sesenta y uno
38 + 35 + 24 = 97
73 + 24
97
27 - 14 + 23 = 36
13 + 23
36
80 - 35 - 30 = 15
45 - 30
15
95 0 71
33 78 3
22 20 17
74 36 3
38 + 35 + 24 = 97
97
27 - 14 + 23 = 36
36
80 - 35 - 30 = 15
15
[Desde aquí 2/2]

97. Unidad 6 - Figuras geométricas78
Líneas perpendiculares
y paralelas
• Intersección de líneas.
• Fundamento sobre el
ángulo recto.
• Líneas paralelas y per-
pendiculares.
• Uso de regla, escuadra
y transportador para
dibujar líneas paralelas
y perpendiculares.
Ángulos
• Concepto de ángulo.
• Elementos de ángulo.
• Ángulo recto.
• Unidad oficial de medi-
da de ángulo: el grado.
• Clasificación de los
ángulos: ángulo recto,
agudo, llano y obtuso.
• Forma de medir y
dibujar ángulos usando
transportador.
Figuras geométricas
• Línea recta.
• Concepto de triángulo y
cuadrilátero.
• Construcción de trián-
gulos y cuadriláteros.
• Elementos de triángulo
y cuadrilátero: vértice y
lado.
Formas de objetos
• Clasificación de objetos
por su forma.
• Superficies planas y
curvas.
• Identificación de figuras
planas.
• Fundamentos de com-
posición y descomposi-
ción de figuras planas.
Triángulos
• Clasificación de trián-
gulos por medida de
sus lados: triángulo
equilátero, isósceles y
escaleno.
• Características de los
ángulos de los trián-
gulos equiláteros y
isósceles.
• Construcción de trián-
gulos equiláteros y isós-
celes usando compás.
• Concepto de perímetro-
Forma de calcular perí-
metros de triángulos y
cuadriláteros.
Círculos y esferas
• Concepto de circunfe-
rencia y círculo.
• Elementos de círculo:
centro, radio y diámetro.
• Construcción de círculo
usando compás.
• Concepto de esfera.
• Elementos de esfera:
centro, radio y diámetro.
Figuras geométricas
• Concepto de rectángulo
y cuadrado.
• Concepto de triángulo
rectángulo.
• Construcción de rec-
tángulos, cuadrados y
triángulos rectángulos.
1
6
• Identifican el concepto de triánglo y cuadrilátero.
Figuras geométricas
Expectativas de logro
(4 horas)Unidad
6
Relación y desarrollo2

98. Guía para maestros/as - Matemática 20
Grado 79
Simetría
• Concepto de figuras
simétricas.
• Eje de simetría.
• Características de figu-
ras simétricas.
• Construcción de figuras
simétricas.
Puntos de lección
• Lección 1: Formemos figuras planas
En primer grado los niños y las niñas tuvieron
la oportunidad de observar diferentes figuras
a través de dibujar las superficies planas de
los objetos. En esta unidad van a aprender el
concepto de triángulo y cuadrilátero como la
figura plana formada por tres y cuatro líneas
rectas respectivamente. Por lo tanto, se hace
necesario introducir la idea de línea recta.
Es imprescindible el uso de reglas para el tra-
zado de las líneas rectas. En caso de no tener
reglas nos podemos auxiliar de objetos que
tengan el borde recto.
Hasta aquí los niños y las niñas pueden pen-
sar que figuras como estas son triángulos.
4
1/4 • Concepto de línea recta
3 Plan de estudio (4 horas)
1. Formemos figuras planas
(4 horas)
2/4~3/4 • Concepto de triángulo y cuadrilátero
• Construcción de triángulos y cuadriláteros
Luego de estudiar esta unidad deben ser ca-
paces de establecer la diferencia entre las
figuras que son triángulos o cuadriláteros y
las que no lo son. Se introducen, además, los
términos de vértice y lado como elementos de
estas figuras.
Uso de la regla para trazar las líneas.
La forma de trazar la línea.
Normalmente las personas diestras trazan la línea hori-
zontal de izquierda a derecha y trazan la línea vertical
de arriba hacia abajo.
Las personas zurdas trazan la línea horizontal de dere-
cha a izquierda y trazan la línea vertical de arriba hacia
abajo. Cuando se tracen las líneas sin necesidad de
medida, es mejor utilizar el lado de la regla que no tiene
las marcas para que no se estropee la escala.
Columnas
4/4 • Lados y vértices del triángulo y el cuadrilátero

99. Unidad 6 - Figuras geométricas80
Formemos figuras planasLección 1:
(1/4)
• Identificar y trazar líneas rectas.
(M) reglas, cuerdas.
(N) reglas.
Objetivo:
Materiales:
5 Desarrollo de
clases
1. Observar el dibujo y comen-
tar. [A1]~[A3]
* Indicar que observen el dibujo
y comenten.
M: ¿Qué diferencia hay entre las
dos cuerdas?
RP: La de María y Luis está más
estirada.
* Aceptar todas las ideas.
M: Vamos a utilizar la regla para
dibujar una línea.
M: ¿Cuál de las cuerdas tiene
una forma parecida a la línea
que dibujaron?
RP: La de María y Luis.
* Explicar que este tipo de lí-
neas se llaman líneas rectas.
2. Encontrar líneas rectas en
su entorno.
M: Vamos a buscar algunas for-
mas que parezcan línea rec-
ta. Pensemos también en las
que hay en nuestras casas,
en las calles, etc.
Que puedan identificar la línea
recta en diferentes objetos,
como el borde de la pizarra,
del LE, los cables del teléfo-
no, de la electricidad, etc.
3. Resolver los ejercicios 1 y 2 .
Se puede hacer la demostración con las cuerdas en el
aula para que los niños y las niñas capten más fácil-
mente la idea de la línea recta.
Lección 1: Formemos figuras planas
Unidad 6
A Conozcamos la línea recta.
62 sesenta y dos
Figuras geométricas
1 Observe y comente acerca de la diferencia entre la forma de las dos cuerdas.
2 Traze una línea utilizando su regla.
3 Compare la línea trazada con las cuerdas.
¿A cuál cuerda se parece la línea trazada?.
4 Encuentre en su entorno formas que parezcan líneas rectas.
María Luis Ana Pedro
La línea que es como la cuerda de María y Luis y la trazada con la
regla se llama “línea recta”.
A la cuerda de María y Luis
1 Dibuje varias líneas rectas utilizando la regla.
2 Una estos punto con una línea recta.
Se omite la solución
(1/4)

100. Guía para maestros/as - Matemática 20
Grado 81
1. Captar el tema de la clase.
[B1]
* Indicar que encierren cada
uno de estos animales. Para
ello deben unir los puntos con
líneas rectas, pero tratando
de utilizar la menor cantidad
de puntos posible.
* Se puede mostrar uno como
ejemplo.
2. Clasificar los animales de
acuerdo al número de lí-
neas que trazaron para en-
cerrarlo. [B2]
M: ¿Cuántas líneas rectas traza-
ron para encerrar al Canguro
y a la Jirafa?
RP: Tres líneas rectas.
M: ¿Cuántas líneas rectas traza-
ron para encerrar al Elefante,
al Hipopótamo y al Rinoce-
ronte?
RP: Cuatro líneas rectas.
3. Definir triángulo y cuadrilá-
tero.
M: ¿Conocen los nombres de
estas figuras que hemos for-
mado para encerrar los ani-
males?
* Muchos niños y niñas, de se-
guro, pueden decir el nombre
del triángulo, pero en caso
del cuadrilátero pueden pen-
sar en rectángulo. Entonces
aprovechamos para introducir
los conceptos.
Continúa en la siguiente página…
63sesenta y tres
B1 Encierre cada uno de los animales trazando líneas rectas uniendo la
menor cantidad de puntos posibles.
La figura cerrada que se forma con tres líneas rectas se llama
“triángulo”.
La figura cerrada que se forma con cuatro líneas rectas se llama
“cuadrilátero”.
¿Cuántas líneas rectas se trazaron para encerrar al Canguro y a la Jirafa?
Tres líneas rectas.
¿Cuántas líneas rectas se trazaron para encerrar al Elefante, al Hipopótamo y
al Rinoceronte?
Cuatro líneas rectas.
2 Divida los animales de acuerdo a las líneas rectas utilizadas para encerrarlos.
El Canguro y la Jirafa
están encerrados con 3
líneas rectas.
El Elefante, el Hipopótamo
y el Rinoceronte están
encerrados con 4
líneas rectas.
(2/4~3/4)
Formemos figuras planasLección 1:
(2/4~3/4)
• Identificar triángulos y cuadriláteros.
(M) reglas.
(N) reglas.
Objetivo:
Materiales:

101. Unidad 6 - Figuras geométricas82
5. Resolver los ejercicios 4 y 5 .
* En el ejercicio 5 , es impor-
tante que los niños y las niñas
se den cuenta que en el caso
de B, D y K no tienen todos
sus puntos conectados, es
decir, la figura no es cerrada
y que en el caso de F, H y J
hay líneas que no son rectas
por eso no son triángulos o
cuadriláteros.
Triángulos ( ) Cuadriláteros ( )
64 sesenta y cuatro
4 De las siguientes figuras cuáles son triángulos y cuáles son cuadriláteros.
3 Complete con la palabra que falta.
Soy una figura cerrada.
Estoy formado por
tres líneas rectas,
mi nombre es _______________
Soy una figura cerrada.
Estoy formado por
cuatro líneas rectas,
mi nombre es _______________
A
B
C
D
E
F
G I
H
J
K
L
M
5 Observe las figuras que no son triángulos ni cuadriláteros.
Piense la razón por la que no lo son y comente con sus compañeros.
C, E, L
Se omite la solución
Triángulo Cuadrilátero
A, G, I, M
Formemos figuras planasLección 1:
(2/4~3/4)
[Desde aquí 3/4]
[Hasta aquí 2/4]
… viene de la página anterior
4. Resolver el ejercicio 3 .
[Continuación]

102. Guía para maestros/as - Matemática 20
Grado 83
6. Resolver el ejercicio 6 y 7 .
* Hacer que los niños y las ni-
ñas recuerden que tener trián-
gulos necesita unir 3 puntos y
para cuadriláteros 4 puntos.
* Es mejor que los niños y las
niñas hagan 2 de cada figura
(de 6 y 7) y si el tiempo no da
se deja de tarea.
Continúa en la siguiente página…
65sesenta y cinco
6 Dibuje varios triángulos conectando puntos con líneas rectas.
Se omite la solución
Formemos figuras planasLección 1:
(2/4~3/4)
[Continuación]

103. Unidad 6 - Figuras geométricas84
7 Dibuje varios cuadriláteros conectando puntos con líneas rectas.
66 sesenta y seis
Se omite la solución
(2/4~3/4)
Formemos figuras planasLección 1:
(2/4~3/4)
… viene de la página anterior
[Continuación]

104. Guía para maestros/as - Matemática 20
Grado 85
67sesenta y siete
C Tracemos líneas rectas para conectar los puntos y formar un triángulo
y un cuadrilátero.
1 ¿Cuántas líneas rectas trazó para formar el triángulo?
3 líneas rectas
2 ¿Cuántos puntos conectó?
3 puntos
(1) (2)
3 ¿Cuántas líneas rectas trazó para formar el cuadrilátero?
4 líneas rectas
4 ¿Cuántos puntos conectó?
4 puntos
Cada línea recta que forma
un triángulo o un cuadrilátero
se llama lado.
Cada punto de la esquina se
llama vértice.
Un triángulo tiene
3 lados y 3 vértices
Un cuadrilátero tiene
4 lados y 4 vértices
lado lado
lado
vértice
vértice vértice lado
lado
lado lado
vértice vértice
vértice
vértice
t
u
w
v
P Q
RS
A
d
e
f
B C
8 Observe las figuras y escriba las letras que corresponden a los lados y a los vértices.
Lados ( )
Vértices ( )
Lados ( )
Vértices ( )
Pueden haber diferentes resultados
(4/4)
d, e, f
A, B, C
P, Q, R, S
t, u, v, w
1. Dibujar un triángulo y un
cuadrilátero. [C]
* Pedirles que tracen líneas
rectas para conectar los pun-
tos y formar un triángulo y un
cuadrilátero.
M: ¿Cuántas líneas rectas traza-
ron y cuántos puntos conecta-
ron para dibujar cada figura.
RP: Tres líneas rectas y tres pun-
tos para dibujar el triángulo.
Cuatro líneas rectas y cuatro
puntos para el cuadrilátero.
2. Conocer los nombres de
vértices y lados.
* Verificar si algún niño o niña
sabe los nombres de lados y
vértices, de ser así aprove-
char sus ideas para hacer la
explicación. De lo contrario
presentarlos haciendo la ex-
plicación necesaria.
3. Resolver el ejercicio 8 .
Formemos figuras planasLección 1:
(4/4)
• Identificar vértices y lados de triángulos y cuadriláteros.
(M) reglas.
(N) reglas.
Objetivo:
Materiales:

105. Unidad 7 - Multiplicación86
7
• Construyen el concepto de multiplicación como abreviación de la adición de sumandos iguales.
• Desarrollan las tablas de la multiplicación del 1 al 9.
• Resuelven problemas de la vida real aplicando la multiplicación.
Multiplicación
Expectativas de logro
(35 horas)Unidad
1
7
Multiplicación
Multiplicación cuyo
producto sea menor que
1,000,000
• U x UMCDU, sin reagru-
par.
• U x DMUMCDU, sin re-
agrupar y reagrupando
(todos los casos).
• DU x DU, sin reagrupar
y reagrupando (todos
los casos).
• DU x CDU, UMCDU, sin
reagrupar y reagrupan-
do (todos los casos).
Multiplicación
Multiplicación cuyos facto-
res sean menores que 10
• Sentido de la multiplica-
ción.
• Tabla de multiplicación
de 2 y 5.
• Tabla de multiplicación
de 3, 4, 6, 7, 8, 9.
• Tabla de multiplicación
de 1.
• Propiedad conmutativa
de la multiplicación.
Multiplicación
Multiplicación cuyo
producto sea menor que
10,000
• Tabla de multiplicación
de 0.
• U x D0, C00, sin reagru-
par.
• U x DU, sin reagrupar
• U x DU, reagrupando
una y dos veces, a la
centena, a la decena y
a ambas.
• U x CDU, reagrupando
una, dos y tres veces.
División
División cuyo dividendo
sea menor que 10,000
y cuyo divisor sea de un
dígito
• Sentidos de la división
“equivalente” e “inclui-
da”.
• DU / U = U, sin y con
residuo.
• DU / U = DU, sin y con
residuo.
• CDU / U = CDU, DU, sin
y con residuo.
• UMCDU / U = UMCDU,
CDU, DU, sin y con
residuo.
Operaciones combinadas
• Orden de cálculo.
• Uso de paréntesis.
• Propiedad asociativa de
la adición.
• Propiedad asociativa de
la multiplicación.
División
División cuyo dividendo
sea menor que 10,000
• UMCDU / U.
• DMUMCDU / U.
• Formas de encontrar el
número para probar.
• DU / DU, sin y con resi-
duo.
• UMCDU, CDU / DU, sin
y con residuo.

106. Guía para maestros/as- Matemática 20
Grado 87
1/3~2/3 • Sentido de la multiplicación
3 Plan de estudio (35 horas)
1. Sumemos y multipliquemos
(3 horas) • Escritura del signo de la multiplicación
• Planteamiento de la operación de la multiplicación
1/122. Multipliquemos
(12 horas)
• Construcción de la tabla del 2
2/12~3/12 • Memorización y aplicación de la tabla del 2
4/12 • Construcción de la tabla del 5
3/3 • Cálculo del producto utilizando adiciones sucesivas
• Términos “factores” “producto”
5/12~6/12 • Memorización y aplicación de la tabla del 5
7/12 • Construcción de la tabla del 3
8/12~9/12 • Memorización y aplicación de la tabla del 3
10/12 • Construcción de la tabla del 4
11/12~12/12 • Memorización y aplicación de la tabla del 4
1/1 • Práctica y dominio de las tablas del 2 al 5 Ejercicios (1) (1 hora)
1/123. Sigamos multiplicando
(12 horas)
• Construcción de la tabla del 6
2/12~3/12 • Memorización y aplicación de la tabla del 6
4/12 • Construcción de la tabla del 7
5/12~6/12 • Memorización y aplicación de la tabla del 7
7/12 • Construcción de la tabla del 8
8/12~9/12 • Memorización y aplicación de la tabla del 8
10/12 • Construcción de la tabla del 9
11/12~12/12 • Memorización y aplicación de la tabla del 9
1/1 Ejercicios (2) (1 hora) • Práctica y dominio de las tablas del 6 al 9
1/14. Multipliquemos con 1
(1 hora)
• Construcción y memorización de la tabla del 1
1/35. Tabla de la multiplicación
(3 horas)
• Construcción y lectura de la tabla de la multipli-
cación de dos dimensiones
2/3 • Regla entre el segundo factor y el producto
3/3 • Propiedad conmutativa de la multiplicación
1/2~2/2 Ejercicios (3) (2 horas) • Práctica y dominio de todas las tablas

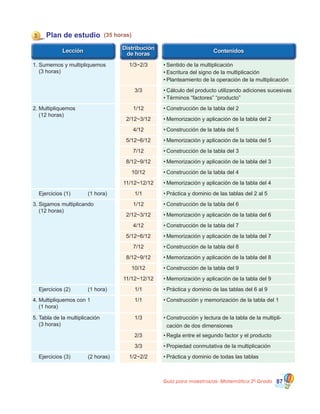
107. Unidad 7 - Multiplicación88
Puntos de lección
• Lección 1: Sumemos y multiplique-
mos
En 1er grado los niños y las niñas realizaron
la actividad de encontrar la cantidad total con-
tando los elementos de los grupos, por ejem-
plo “6 grupos de 10 son 60” relacionándolo
con la comprensión del concepto de núme-
ro. Al desarrollar nuevamente esta actividad,
se orienta a los niños y a las niñas para que
comprendan que, cuando las cantidades de
cada grupo son iguales, la cantidad total del
conjunto de grupos se encuentra utilizando la
multiplicación. Es decir, orientar que cuando
la situación es sobre la adición repetida del
mismo número se utiliza la multiplicación.
En cuanto al sentido de la multiplicación (véa-
se Columnas) es importante que los niños y
las niñas capten la cantidad total como “tan-
tos grupos de tantos”, aclarando los siguien-
tes dos puntos:
1: ¿Cuál es el número que representa la can-
tidad en cada grupo?
2: ¿Cuántos grupos de ese número hay?
Por eso se debe presentar las situaciones don-
de las cantidades en cada grupo sean iguales
y las cantidades en cada grupo sean distintas
para que se den cuenta de la diferencia que
existe entre ambas situaciones y comprendan
cuándo se puede utilizar la multiplicación.
También es muy importante que los niños y
las niñas imaginen claramente la situación del
problema. O sea que no hagan el PO sólo con
observar los números que aparecen en el pro-
blema sin importar el significado de cada uno
de ellos. Por lo tanto para lograr que tengan
conciencia de la cantidad en cada grupo y la
cantidad de grupos se puede hacer que utili-
cen los materiales concretos.
Se introduce esta lección con cantidades
discretas pero después de entender el sen-
tido de la multiplicación se utilizan tambien
las cantidades continuas (véase Columnas),
pensando que aunque no se ha tocado toda-
vía las unidades oficiales de las magnitudes
como son el peso, la longitud etc., éstas se
usan frecuentemente en la vida cotidiana de
los niños y las niñas.
• Lección 2: Multipliquemos
En esta GM, que tiene por regla de apegar-
se a los contenidos del currículo nacional, se
pone como base el método
[8 x 2; 8 por 2 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2]
Por lo tanto, en la construcción de la tabla
de multiplicación, para encontrar la respues-
ta, que los niños y las niñas calculen de la
siguiente manera:
2 x 1 = 1 + 1; 2 x 2 = 2 + 2; 2 x 3 = 3 + 3;...
Además, es efectivo introducir primero la
construcción de la tabla del 2 y del 5 porque
así ellos pueden encontrar la respuesta de
cada multiplicación rápidamente aplicando su
experiencia de contar de 2 en 2 y de 5 en 5,
que ya han aprendido.
En la construcción de la tabla de la multipli-
cación se orienta a los niños y a las niñas te-
niendo en cuenta los siguientes puntos:
1: Que capten el sentido de la multiplicación
asociándolo con el uso de materiales con-
cretos.
2: Que capten que se puede encontrar la
cantidad total sumando sucesivamente la
cantidad en cada grupo tantas veces como
la cantidad de grupos existentes.
3: Que comprendan la forma de la construc-
ción de la tabla de la multiplicación, es de-
cir, si el segundo factor aumenta en 1, el
resultado aumenta en la cantidad del pri-
mer factor [Ejemplo: como 2 x 3 = 6, 2 x 4
= 6 + 2 = 8] y que pueden construir la tabla
fácilmente por sí mismos en caso de que
la olviden. Al mismo tiempo, que sientan la
conveniencia y la rapidez del cálculo si se
memoriza la tabla.
Con el método de construcción de la tabla de
la multiplicación se hace énfasis en el sentido
de la multiplicación y la utilidad de la tabla tan-
to como en la memorización de la misma.
En la tabla del 2 y del 5, el estudio puede ser
conducido por el maestro o la maestra, pero
es mejor planificar el proceso del estudio de la
tabla del 3 y del 4 de manera que los niños y
las niñas al manejar los materiales concretos,
sean quienes construyan esas tablas apli-
4

108. Guía para maestros/as- Matemática 20
Grado 89
cando lo aprendido (véase Columnas) bajo
la perspectiva de que se puede encontrar el
producto¹ sumando el primer factor² una
vez más al producto anterior de la tabla. Es
decir, que no es necesario empezar a sumar
desde el principio sino que cuando aumenta
en 1 el segundo factor³, el producto aumenta
una vez más la cantidad del primer factor.
Durante toda la unidad se utiliza la colección
de pelotas, las tarjetas de la multiplicación y
la hoja de la memorización como un medio
para la construcción, práctica y memorización
de las tablas.
• Lección 3: Sigamos multiplicando
Siguiendo los contenidos de la lección 2, el
punto de esta lección es que los niños y las
niñas construyan por sí mismos las tablas de
multiplicación aplicando el método de la cons-
trucción de la tabla de multiplicar. A partir de
la construcción de la tabla del 6 se utiliza el
dibujo de la colección de pelotas (véase Co-
lumnas) para que ellos se alejen poco a poco
de los materiales concretos y puedan pensar
con los dibujos abstractos, en las tablas del 8
y del 9 los niños y las niñas construirán las ta-
blas observando la relación entre el segundo
factor y el producto.
• Lección 4: Multipliquemos con 1
La tabla del 1, cuyo primer factor es 1, es don-
de los niños y las niñas tienen la dificultad de
sentir la necesidad de multiplicar. Se enseña
teniendo conciencia del sentido de la multipli-
cación, es decir que “cuántas veces tiene 1”,
asociando con ejemplos de la vida cotidiana.
También es importante que los niños y las ni-
ñas capten que cuando se multiplica cualquier
número por 1, siempre el producto será igual
al primer factor.
• Lección 5: Tabla de la multiplicación
Esta lección trata de la característica o regla
de la multiplicación (propiedad conmutativa
de la multiplicación). Generalmente en este
punto, sobre la propiedad conmutativa de la
multiplicación, al estudiar la tabla de la mul-
tiplicación en 2do grado, los maestros y las
maestras lo explican diciendo a los niños y a
las niñas cosas como por ejemplo “2 x 3 y 3 x
2 da lo mismo”, etc.; por la conveniencia de la
dirección. Sin embargo esta manera no cultiva
el placer de aprender en los niños y las niñas,
es mejor utilizar la actividad de formar la tabla
de dos dimensiones para que descubran por
su propio esfuerzo que cuando el segundo
factor aumenta en 1, el producto aumenta en
1 vez la cantidad del primer factor y aunque
cambian el primer factor y el segundo factor el
producto no cambia. Además se espera culti-
var el sentido o la percepción de los números
observando toda la tabla de multiplicación de
dos dimensiones, por ejemplo, hay números
que aparecen muchas veces (16, 24, etc.)
hay números que aparecen solamente una
vez (49, 81, etc.) y hay una regla interesante
para la colocación de 16 ó 24, etc.
¹ El producto, es el resultado de la operación de la multiplicación, que representa el resultado del cálculo de la multiplicación.
² El primer factor es el elemento del planteamiento de la operación de la multiplicación, que representa a la cantidad de grupos. (Las
veces que se hace la adición sucesiva.)
³ El segundo factor es el elemento del planteamiento de la operación de la multiplicación, que representa a la cantidad de grupos.
(Lo que se suma sucesivamente.)

109. Unidad 7 - Multiplicación90
Hay dos maneras de hacer el planteamiento de la operación.
Situación: Hay 3 platos y dos manzanas en cada plato.
PO:
A) 3 x 2 = 6 (Se lee “tres veces dos es igual a seis”). En este caso, 3 x 2 quiere decir 2 + 2 + 2.
B) 2 x 3 = 6 (Se lee “dos veces tres es igual a seis”). En este caso, 2 x 3 quiere decir 3 + 3.
El CNB ha adoptado la forma (A), por lo tanto esta es la forma que usaremos en esta GM.
Las cantidades discretas y las cantidades continuas
Las cantidades discretas: son las cantidades que representan a las cantidades enteras de objetos.
Para ello se utiliza al conjunto de los números naturales {1, 2, 3, 4, 5, etc.}.
(Ejemplo: 1 vaca. En este caso no se puede cambiar la unidad ni expresar con diferente número. Una
vaca es siempre una vaca.)
Las cantidades continuas: son aquellas que, cuando se decide alguna unidad, el número que las repre-
senta puede ser cualquiera del conjunto de los números reales {0, 1/2, 0.25, 3.1415924..., 4, etc.}. Entre
los ejemplos de las cantidades continuas se tiene la longitud, el peso, la capacidad, etc. A diferencia
de las cantidades discretas, los números continuos representan a las características cuantitativas de
sustancias que no necesariamente son enteras, pero que no cambian en su esencia.
(Ejemplo: 1 litro de leche. Si se decide como la unidad el mililitro, el número se convierte a 1,000 milili-
tros aunque sea la misma cantidad.)
Aplicación de lo aprendido
Es necesario idear la mejor manera para que los niños y las niñas puedan adelantar el estudio por sí
mismos aplicando lo aprendido. Para eso, es mejor pegar en la pared del aula láminas con contenidos
relacionados sobre lo aprendido o que muestren ordenadamente o insinúen la ventaja de cada forma
de razonar para que lo utilicen según la necesidad.
También es importante que los niños y las niñas tengan conciencia de la ventaja de estudiar “aplicando
lo aprendido” mediante actividades donde necesitan recordar lo aprendido o darse cuenta de la ventaja
de ese método dentro del desarrollo de la clase. Así los niños y las niñas aprenderán no solamente los
contenidos sino también “como estudiar para (aprender)”.
Ejemplo de la orientación general para la memorización de las tablas
Se presenta un ejemplo con la tabla del 2.
1: Hacer que los niños y las niñas repitan unas dos veces, desde “2x1” hasta “2x9”, observando la tabla.
2: Cubrir el producto de “2x1” (cubrir el producto con un papelito del mismo tamaño de la letra del produc-
to. Es mejor pegar con masking-tape solamente en la parte superior de manera que se pueda levantar el
papel para ver el producto.
3: Preguntar a los niños y a las niñas: “¿Dos por uno es?”, y que contesten: “Dos”. Repetir algunas veces
para que memoricen.
4: Hacer que los niños y las niñas digan desde “2x1” hasta “2x9”, dejando el producto de “2x1” cubierto.
5: Cubrir el producto de “2x2” con otro papelito.
El sentido de los factores en la multiplicación
Columnas
1
2
3
4

110. Guía para maestros/as- Matemática 20
Grado 91
6: Preguntar a los niños y las niñas: “¿Dos por dos es?”, y que contesten: “Cuatro”. Repetir algunas veces
para que memoricen.
7: Dejando el producto de “2x1” y “2x2” cubiertos, hacer que los niños y las niñas digan la tabla desde
“2x1” hasta “2x9”.
8: Repitiendo de la misma manera, finalmente, los niños y las niñas podrán decir la tabla con todos los
productos cubiertos.
* Pegando en la pared del aula la lámina de la tabla con los productos que fueron cubiertos, los niños y las
niñas podrán practicar la memorización de la tabla libremente con la alegría de confirmar sus respuestas
al abrir los papelitos.
[Variación de la práctica de la tabla]
En el caso de la orientación grupal es mejor cambiar la forma de decir la tabla para que aumente el
entusiasmo en los niños y las niñas.
Todos juntos Fila por fila Los niños y las niñas alternadamente Uno por uno en orden
Uno por uno al azar etc.
De 2x1 hasta 2x9 seguida Un niño o una niña o un grupo dice 2x1, después otro niño o niña o
grupo dice 2x2, y así cambiando el turno etc.
La práctica de la tabla de la multiplicación
En la práctica de cada tabla de multiplicación están los pasos siguientes:
1: Decir la tabla correctamente observando el P.O. u observando la colección de pelotas.
2: Decir desde 2x1 hasta 2x9 en orden.
3: Decir desde 2x9 a 2x1 (de abajo para arriba, y al revés)
4: Decir al azar.
En esta GM se planea dos horas para cada tabla como el tiempo de memorización y aplicación de la
misma. En estas horas sería mejor orientar mediante las formas 1 y 2 principalmente, y que las formas
3 y 4 las desarrollen de ahora en adelante para que memoricen la tabla con solidez. Para eso, es mejor
que todos los días ellos/as practiquen las tablas, más o menos 5 minutos al día (por ejemplo: decir la
tabla cada uno, inmediatamente después de llegar a la escuela, antes de entrar a clase, antes de salir
al recreo, antes de salir de la escuela para la casa, etc.). Que los niños y las niñas memoricen las tablas
apropiadamente para que puedan tener la base de poder comprender los estudios del 3er grado en
adelante sin problema.
El uso de la colección de pelotas
La colección de pelotas se cubre con una hoja de papel (o con la mano). Es muy ilustrativo usarla en
el paso de la construcción de las tablas y además en la práctica de las tablas. Como se utiliza durante
la unidad, sería mejor dibujar en una lámina las pelotas para la tabla del 9 y cada vez se puede utilizar
doblada de modo que muestre solamente la parte que representa la tabla necesaria.
1: La cantidad de pelotas verticales representan la cantidad en cada grupo, es decir es el número que
se repite. La cantidad de las pelotas verticales representan la cantidad de grupos, es decir, es el nú-
mero de veces.
2: Se puede presentar la situación y el producto de la multiplicación moviendo horizontalmente el papel
que cubre los grupos.
3: Los niños y las niñas pueden construir las tablas con la ayuda de la colección de pelotas y también
pueden decir la tabla percibiendo visualmente la dimensión de la cantidad.
5
6

111. Unidad 7 - Multiplicación92
(Ejemplo de la tabla del 2)
El uso de las tarjetas de la multiplicación
La manera fundamental de practicar las tablas de la multiplicación usando las tarjetas de la multiplicación es
la siguiente. Es recomendable que inventen cualquier otra manera con las ideas del maestro o la maestra y
de los niños y las niñas y que las utilicen pensando en la situación actual de los niños y las niñas.
El maestro o la maestra puede preparar las tarjetas del tamaño ampliado y usarlas para la práctica de la
memorización.
Es recomendable tomar los primeros 3~5 minutos de cada hora de clase para practicar todos juntos ya
que la clave de la memorización es practicar todo los días.
[Uso individual]
A: Colocar las tarjetas en orden y al azar, y decir los productos del reverso observando el PO de la
cara. (Se puede hacer que los niños y las niñas coloquen alguna marca en las tarjetas con las que se
equivocaron y que practiquen principalmente con ellas.)
B: Colocar las tarjetas en orden y al azar, y decir el PO de la cara observando los productos del reverso.
C: Realizar las prácticas de (A) o (B), con varias tablas de la multiplicación.
[Uso en pareja]
A: Un niño o niña muestra la cara de la tarjeta y el otro u otra contesta el producto observando esa
tarjeta. Repetir esta actividad alternativamente. (O también hasta cuando un participante conteste co-
rrectamente cambiar los papeles o se puede hacer la competencia de contestar correctamente 5 veces
por cada participante.)
B: Cada uno de los niños o niñas prepara al azar las tarjetas de la misma tabla (es mejor que preparen
las tarjetas de sólo una o dos tablas). Poner una tarjeta en el pupitre al mismo tiempo con la cara hacia
arriba, leer el PO y contestar observando su tarjeta. El o la que tenga el producto mayor gana.
C: Colocar en el pupitre las tarjetas con la cara hacia arriba, un niño o niña escoge una, lee el PO y
contesta el producto. Mirar el producto del reverso y si contestó correctamente toma esa tarjeta y puede
continuar con otra tarjeta. Si se equivoca pierde su turno y no puede tomar la tarjeta. El que consiga
más tarjetas gana. (Se puede hacer que cambien el turno alternadamente.)
[Uso en pareja o en grupo]
A: Colocar las tarjetas en el pupitre con el reverso (el producto) hacia arriba. Un niño o niña preguntará
a sus compañeros y compañeras diciendo el PO de las tablas que están en el pupitre. Los demás bus-
carán el producto de esa pregunta y tomarán una de las tarjetas que tiene ese producto. El que consiga
más tarjetas gana.
B: Colocar las tarjetas en el pupitre con la cara (el PO) hacia arriba y un niño o niña preguntará diciendo
el producto al PO de las tablas que están en el pupitre. Los demás buscarán el PO de esa pregunta y
tomarán una de las tarjetas que tiene ese PO. El que consiga más tarjetas gana.
7

112. Guía para maestros/as- Matemática 20
Grado 93
El uso de la hoja de memorización
Esta hoja es para elevar el entusiasmo de la memorización de la tabla en los niños y las niñas y para
confirmar el progreso o avance. Hay que tener cuidado de no provocar la caída del entusiasmo de la
memorización al apresurarlos demasiado. El uso de la hoja también se puede cambiar según las cir-
cunstancias y situaciones de los niños y las niñas de la clase.
1) Hay tres formas de memorizar las tablas que son: “en orden”, “de abajo para arriba” y “en desorden”.
Los niños y las niñas las practican para que puedan decir las tablas de cualquier manera.
2) Los niños y las niñas pueden practicar y desafiar primero en cualquier tabla aprendida y de cualquier
manera.
3) Cuando tengan confianza de la memorización, los niños y las niñas buscarán el tiempo libre (en
el receso, antes de empezar la primera clase, después de terminar la clase) para que el maestro o la
maestra escuche la memorización de ellos. Cuando pueda decir la tabla completa de una manera, re-
cibirá la firma del maestro o la maestra.
4) Los que recibieron la firma del maestro o la maestra pueden ser los “estudiantes monitores”. Y po-
drán escuchar el desafío de sus compañeros y compañeras en lugar del maestro o la maestra. Des-
pués de aprobar el nivel de la memorización de los compañeros y compañeras que desafiaron pueden
darle su firma.
5) El “estudiante monitor” puede escuchar el desafío de sus compañeros y compañeras solamente para
las tablas y las maneras en las que recibió la firma del maestro o la maestra. Por lo tanto, los demás
buscarán al compañero o compañera monitor que tenga la firma del maestro o la maestra en la casilla
que ellos quieran desafiar.
6) Cuando tengan las firmas del maestro o la maestra, o del estudiante monitor, en todas las casillas,
pueden recibir el diploma. Si se cometen errores en la memorización, después de practicar nuevamen-
te, se puede desafiar muchas veces más hasta que venza el desafío.
* Se adopta la manera en que los estudiantes monitores también firman a otros compañeros o compa-
ñeras para que los niños y las niñas se apoyen y colaboren mutuamente, y también para utilizar el tiem-
po efectivamente. En este caso es mejor que el maestro o la maestra confirme el nivel de la memoriza-
ción aprobado por el estudiante monitor, llamándoles según la necesidad. Cuando ellos puedan decir
correctamente la tabla es mejor que les felicite, a ese niño o niña y al estudiante monitor que firmó a su
compañero o compañera. A través de la felicitación los estudiantes monitores tendrán más entusiasmo
de aprobar a su compañero o compañera en la memorización con responsabilidad y juicio justo.
* Se puede decidir sobre cuál práctica hay que hacer como mínimo antes de desafiar nuevamente
cuando fracasen al desafío. (Por ejemplo: decir más de 5 veces el PO. donde se equivocó y decir toda
la tabla más de 2 veces antes de desafiar de nuevo, etc.)
* El maestro o la maestra debe recoger las hojas frecuentemente para chequear el progreso de los
niños y las niñas y también deben tener en cuenta la motivación y orientación individual para los niños
y niñas con dificultad para avanzar.
8

113. Unidad 7 - Multiplicación94
Sumemos y multipliquemosLección 1:
(1/3~2/3)
• Conocer el sentido de la multiplicación y expresar la
situación de ésta en el PO con el signo “x”.
(M) habichuelas, tapitas, piedrecitas.
(N) habichuelas, tapitas, piedrecitas.
Objetivo:
Materiales:
5 Desarrollo de
clases
1. Comentar lo observado en el
dibujo y captar el tema. [A]
M: ¿Que observan en el dibujo?
Vamos a encontrar la cantidad
total de cada fruta.
2. Encontrar la cantidad de
guineos. [A1]
M: Primero, ¿cuántos guineos hay
en total?
Que encuentren ya sea con-
tando, sumando, o como ellos
quieran, sustituyendo los gui-
neos por los materiales.
3. Pensar en la forma de encon-
trar la cantidad de manzanas.
[A2]
M: Vamos a colocar las habichue-
las, tapitas o piedrecitas del
mismo modo que las manza-
nas.
* Se puede confirmar la forma de
colocar las habichuelas, tapitas o
piedrecitas (3 grupos de 5) en pa-
reja.
M: ¿Cuántas manzanas hay en
total? ¿Cómo hicieron?
* Después de aceptar todas las
ideas, concluir con la adición
sucesiva.
M: ¿Cuántas canastas hay?
¿Cuántas manzanas hay en
cada canasta? ¿Cuántas
manzanas hay en total?
* Confirmar la relación entre las
cantidades “3 canastas y 5
manzanas en cada canasta.
Son 15 manzanas en total”.
4. Pensar la diferencia entre las
formas en que se metieron
los guineos y las manzanas.
[A3]
Continúa en la siguiente página…
Es difícil sumar sucesivamente y escribir el PO cuando
los factores son números grandes como el caso de los
mangos (8 mangos en cada una de las 9 canastas). A
través de esta experiencia, que los niños y las niñas vean la
conveniencia y la ventaja de utilizar la multiplicación y que despier-
ten el entusiasmo para aprender las matemáticas. Este tipo de pensa-
miento o actitud de buscar la facilidad, la conveniencia o la rapidez es
un fundamento para desarrollar las habilidades matemáticas.
Planteamiento de la operación: ____________________ Respuesta: _____________
Lección 1: Sumemos y multipliquemos
Unidad 7
A Encuentre la cantidad de frutas.
68 sesenta y ocho
Multiplicación
1 ¿Cuántos guineos hay en total?
2 ¿Cuántas manzanas hay en total?
+
3 ¿Qué diferencia hay entre los guineos y las manzanas por la forma en que están metidos
en la canastas?
4 Encuentre la cantidad total de las otras frutas con la suma.
12 guineos
Respuesta: 15 manzanas
Planteamiento de la operación: ____________________
Hay canastas y manzanas en cada canasta. Son manzanas en total.3 5 15
Hay canastas y naranjas en cada canasta. Son naranjas en total.
Hay canastas y piñas en cada canasta. Son piñas en total.
Hay canastas y mangos en cada canasta. Son mangos en total.
Planteamiento de la operación: 5 + 5 + 5 = 15
Respuesta: _____________
Planteamiento de la operación: ____________________ Respuesta: _____________
3 + 3 + 3 + 3 = 12 12 naranjas
(1/3 ~ 2/3)
La cantidad de manzanas
que hay en cada canasta
es la misma.
La cantidad de guineos
que hay en cada canasta
no es la misma. (es diferente)
4 3 12
5 2 10
9 8 72
2 + 2 + 2 + 2 + 2 = 10 10 piñas
8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 72 72 mangos

114. Guía para maestros/as- Matemática 20
Grado 95
Lección 1:
(1/3~2/3)
Sumemos y multipliquemos
[Continuación]
… viene de la página anterior
5. Encontrar la cantidad total de
otras frutas. [A4]
* Indicar que coloquen las habi-
chuelas u otro material del mismo
modo que las frutas y que confirmen
que en cada canasta hay la misma
cantidad de frutas y luego que en-
cuentren el total con la suma.
Que sientan la inconveniencia de
sumar muchas veces (véase Notas).
6. Expresar la cantidad total de man-
zanas con el PO y conocer su lec-
tura y el término “multiplicación”.
M: Hay una forma mucho más fácil
que la suma para escribir esta
situación en el PO.
* Explicar que se puede escribir la situ-
ación de “3 canastas y 5 manzanas
en cada canasta, son 15 manzanas”
con el PO “3 x 5 = 15” y a esta oper-
ación se le llama “la multiplicación”.
Que capten que el PO de la mul-
tiplicación es la representación
de la relación de “cantidad de ca-
nasta por la cantidad”.
M: ¿Se puede escribir la cantidad to-
tal de los guineos también con la
multiplicación? ¿Por qué?
Que confirmen que no se puede
por no tener la misma cantidad
en cada canasta y que capten el
sentido de la multiplicación.
7. Representar la cantidad total
de otras frutas con la multipli-
cación. [A5]
Que sientan la facilidad de escri-
bir el PO con la multiplicación que
con la suma sucesiva.
* Darotrosejerciciosparaconfirmar
el concepto de la multiplicación,
por ejemplo, escribir en la pizarra
“4 x 6” e indicar que coloquen las
habichuelas, tapitas o piedrecitas
representando la situación, etc.
8. Resolver los ejercicios 1 y 2 .
[Hasta aquí 1/3]
[Desde aquí 2/3]
Planteamiento
de la operación: ___________
Planteamiento
de la operación: ___________
Planteamiento
de la operación: ___________
Planteamiento
de la operación: ___________
69sesenta y nueve
1 Escriba el planteamiento de la operación de la multiplicación para encontrar la
cantidad total de cada tipo de verduras.
5 Represente la cantidad total de cada fruta de la página anterior en el planteamiento
de la operación de la multiplicación.
Se puede representar esta situación con el planteamiento de la operación.
Cantidad
de canastas
Cantidad en
cada canasta
Cantidad
total
Este tipo de operación se llama multiplicación.
Es el cálculo para encontrar la cantidad total cuando los grupos tienen la misma
cantidad.
X
2 1
2 Dibuje los círculos de modo que represente los siguientes planteamientos de la operación
(1) 2 x 4 (2) 4 x 2 (3) 4 x 3
X
X
X
3 x 5 = 1 5
manzanas.15manzanas en cada canasta, son5canastas y3
¡Que fácil!
No se necesita repetir
escribiendo la suma
muchas veces,
¿verdad?
Cada grupo se puede encerrar con el otro círculo o con la otra figura.
Lo importante es representar correctamente 2 grupos de 4.
6 x 5
2 x 8
3 x 2
5 x 4
9 8
5 2
4 3

115. Unidad 7 - Multiplicación96
Sumemos y multipliquemosLección 1:
(3/3)
• Calcular el producto sumando sucesivamente la can-
tidad del multiplicando tantas veces como se indica
en la cantidad del multiplicador.
(M) habichuelas, tapitas, piedrecitas.
(N) habichuelas, tapitas, piedrecitas.
Objetivo:
Materiales:
1. Leer el problema y captar
su situación. [B]
M: ¿Con qué operación se puede
encontrar cuántos huevos hay
en total? ¿Por qué?
Que capten que se puede usar
la suma y también la multiplica-
ción por haber la misma canti-
dad de huevos en cada nido.
2. Escribir el PO. [B1]
3. Pensar en la forma de encon-
trar el resultado de “4 x 5”.
[B2]
M: ¿Cómo encontramos el resul-
tado de “4 x 5”?
* Concluir que se puede encon-
trar con la adición sucesiva.
* Se puede hacer que los niños y
las niñas usen las habichuelas, ta-
pitas o piedrecitas para confirmar
la cantidad en cada nido y la canti-
dad de nidos.
4. Encontrar la respuesta. [B3]
* Fijar que después de encon-
trar el resultado del cálculo,
hay que escribir la respuesta
con las unidades relacionan-
do con la pregunta.
5. Conocer los términos “fac-
tores” y “producto” y su
sentido.
* Confirmar que el 4 es la canti-
dad de grupos (nidos) que re-
presentan el número de veces
que se repite y que el 5 es la
cantidad (de huevos) en cada
grupo (nido) que representa el
número que se repite (para su-
mar) relacionando con el dibujo
y el PO de la suma sucesiva.
6. Resolver el ejercicio 3 .
(Véase Notas)
Si hay niños y niñas que tienen dificultades, se puede
hacer que piensen en el PO después de captar bien la
situación de “cuántos en cada grupo” y “cuántos grupos”,
colocando las habichuelas, tapitas o piedrecitas, correspon-
diendo al problema y su ilustración. Después, que ellos encuentren
el producto utilizando la forma de la adición sucesiva observando el PO
o la colocación de las habichuelas, tapitas o piedrecitas.
70 setenta
B Hay 4 nidos, si hay 5 huevos en cada
nido. ¿Cuántos huevos hay en total?
2 Piense en la forma de encontrar la
respuesta de la operación.
3 Resuelva los siguientes problemas.
El producto de "4 x 5" se puede
encontrar con la suma sucesiva
de "5 + 5 + 5 + 5".
3 ¿Cuántos huevos hay en total?
Planteamiento
de la operación: 4 x 5 = 20
Respuesta: 20 huevos.
Hay 4 jaulas, si hay 3 conejos en cada jaula. ¿Cuántos conejos hay en total?
(Ejemplo)
Forma de encontrar el producto
3 + 3 + 3 + 3
Planteamiento
de la operación: 4 x 3 = 12
Respuesta: 12 conejos
(1) Hay 6 motos, si cada moto tiene 2 llantas. ¿Cuántas llantas hay en total?
Forma de encontrar el producto
(2) Hay 3 cajas, si en cada caja hay 8 pelotas. ¿Cuántas pelotas hay en total?
Forma de encontrar el producto
PELOTAS PELOTAS PELOTAS
(3) Hay 5 platos, si hay 4 pasteles en cada plato. ¿Cuántos pasteles hay en total?
Forma de encontrar el producto
Producto1er factor
Cantidad
de grupos
(Número de veces
que se repite)
Cantidad
total
2do factor
Cantidad en
cada grupo
(Cantidad que
se repite)
4 x 5 = 20
1 Escriba el planteamiento de la
operación de la multiplicación.
4 x 5
Planteamiento
de la operación:
Respuesta:
Planteamiento
de la operación:
Respuesta:
Planteamiento
de la operación:
Respuesta:
2 + 2 + 2 + 2 + 2 + 2 12 llantas
6 x 2 = 12
8 + 8 + 8 24 pelotas
3 x 8 = 24
20 pasteles
5 x 4 = 20
4 + 4 + 4 + 4 + 4
(3/3)

116. Guía para maestros/as- Matemática 20
Grado 97
Lección 2:
(1/12)
Objetivo:
Materiales:
Multipliquemos
• Construir la tabla del 2.
(M) habichuelas, tapitas, piedrecitas.
(N) habichuelas, tapitas, piedrecitas.
1. Leer el problema y captar
su sentido. [A]
M: Cuántos árboles hay. Cuántos
mangos hay en cada árbol.
Que capten que la cantidad
de grupo es 2 (árboles) y en
cada grupo es 4 (mangos) y
la cantidad.
* Para los niños y las niñas que
tienen dificultades para ima-
ginar la situación, se puede
preguntar cuál es el número
que se suma repetidamente y
cuántas veces.
2. Escribir el PO. [A1]
3. Encontrar la cantidad total
de los mangos hasta el caso
de 4 mangos en cada árbol,
paso a paso. [A2]
* Indicar que escriban el PO y
la forma de encontrar el pro-
ducto (la suma sucesiva) y el
producto hasta para el caso
de 4 árboles, consultando la
ilustración y el ejemplo del
caso de “2 x 1”.
* Se puede hacer que utilicen las ha-
bichuelas, tapitas o piedrecitas.
4. Expresar el resultado y confir-
mar la respuesta del problema.
5. Analizar la forma en que au-
menta el producto. [A3]
M: ¿Pueden adivinar cuál es el
producto de 2 x 5? ¿Por qué?
Que se den cuenta que se au-
menta de 2 en 2.
M: ¿Por qué los productos au-
mentan de 2 en 2?
RP: Porque hay 2 árboles y cada
árbol aumenta un mango en
cada fila.
6. Encontrar los productos has-
ta “2 x 9”. [A4]
* Después de escuchar los re-
sultados, concluir la caracte-
rística de la tabla del 2.
7. Leer la tabla del 2. [A5]
(Véase Notas.)
En este caso, es mejor que lo lean de manera formal,
como por ejemplo, “dos por uno es igual a dos”. En el
paso de la memorización, se puede practicar diciendo,
por ejemplo, “dos por uno, dos”.
Orientar que pueden tratar de memorizarla en la casa. Pero, no es
necesario obligarles todavía ya que el proceso de memorización lleva
tiempo.
71setenta y uno
A Si hay 2 árboles y cada uno tiene 4 mangos, ¿cuántos mangos hay en total?
1 Escriba el planteamiento de la operación.
2 Encuentre el total de mangos paso a paso hasta el caso de 4 mangos
en cada árbol.
Lección 2: Multipliquemos
2 x 4
Respuesta: 8 mangos
(1) ¿Cuál es el producto de 2 x 5? ¿Por qué?
El producto de 2 x 5 es 10. Porque los productos aumentan de 2 en 2.
(2) Confirme el producto de 2 x 5 llenando la tabla.
Forma de encontrar el producto Producto
2 x 1 1 + 1 2
2 x 2 2 + 2
3 Observe los productos de 2 x 1 a 2 x 4 y piense.
4 Encuentre los productos de
2 x 6 a 2 x 9 llenando la tabla.
5 Lea la tabla del 2.
Los productos de la tabla del 2
aumentan de 2 en 2.
Se pueden encontrar sumando
2 al producto anterior.
2 x 1 = 2
Dos por uno es igual a dos.
2 x 2 = 4
Dos por dos es igual a cuatro.
Planteamiento de la operación: 2 x 4 = 8
4
Planteamiento
de la operación
2 x 3 3 + 3 6
2 x 4 4 + 4 8
2 x 5 5 + 5 10
2 x 6 6 + 6 12
2 x 7 7 + 7 14
2 x 8 8 + 8 16
2 x 9 9 + 9 18
(1/12)

117. Unidad 7 - Multiplicación98
MultipliquemosLección 2:
(2/12~3/12)
• Memorizar y aplicar la tabla del 2.
(M) tarjetas de la multiplicación.
(N) tijeras, clip, sobre.
Objetivo:
Materiales:
1. Captar el tema. [B]
2. Escribir la tabla del 2 y leer-
la. [B1]
* Puede leer en la forma prácti-
ca, “dos por uno, dos”.
* Se puede aprovechar el tiem-
po, elaborando la tabla en la
lámina para la pizarra junto
con los niños y las niñas.
* Dar la orientación general para
la memorización usando la ta-
bla escrita en la lámina (véase
Columnas).
3. Decir la tabla del 2 observan-
do la colección de pelotas.
[B2]
* Explicar el uso de la colección
de pelotas (véase Columnas).
4. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [B3]
* Indicar que esta vez practiquen
individualmente con el uso más
básico (véase Columnas). Ex-
plicar el procedimiento de prác-
tica usando las tarjetas prepara-
da por el maestro o la maestra.
5. Seguir practicando la tabla de
modo que logre memorizar.
B Vamos a practicar la tabla del 2.
72 setenta y dos
1 Escriba la tabla del 2
y léala en orden.
2 Diga la tabla del 2 en orden
observando la colección de pelotas.
Tabla del 2
2 x 1 = 2
3 Haga las tarjetas de la multiplicación y practique con ellas.
(Se puede usar las páginas para recortar.)
4 Escriba su nombre en la hoja de memorización de la tabla de
multiplicación (páginas para recortar) y pídale al maestro o la
maestra la firma cuando pueda memorizar la tabla.
1 Resuelva los siguientes ejercicios.
(1) 2 x 8 = (2) 2 x 2 = (3) 2 x 5 = (4) 2 x 9 = (5) 2 x 3 =
(6) 2 x 6 = (7) 2 x 7 = (8) 2 x 4 = (9) 2 x 1 =
2 Resuelva los siguientes problemas.
Planteamiento de la operación: ______________ Respuesta: ___________
Planteamiento de la operación: ______________ Respuesta: ___________
Planteamiento de la operación: ______________ Respuesta: ___________
(1)
(2)
(3)
Hay 2 llaveros y cada llavero tiene 6 llaves, ¿cuántas llaves hay en total?
Hay 2 niños y cada niño tiene 8 mentas, ¿cuántas mentas hay en total?
María compró 2 cajas y hay 1 pastel en cada caja. ¿Cuántos pasteles tiene María?
Cara Reves
2 x 2
!Correcto!
6
Dos por
tres, seis.
Debes agrupar
las tarjetas en que te
equivocaste y practícalas
muchas veces.
Vamos a decir la
tabla del 2 cubriendo la
parte que no se necesita de
la colección depelotas.
16 4 10 18 6
12 14 8 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 6 = 12
2 x 8 = 16
2 x 1 = 2
16 mentas
2 pasteles
12 llaves
(2/12 ~ 3/12)
2 x 9 = 18
6. Conocer el uso de la hoja de
la memorización de la tabla
de la multiplicación. [B4]
* Explicareluso(véaseColumnas)
y motivar que la utilicen buscan-
do cualquier espacio del tiempo.
7. Confirmar el estado de la me-
morización de la tabla del 2.
* Dar el tiempo para desafiar la
memorización.
8. Resolver los ejercicios 1 y 2 .
[Hasta aquí clase]

118. Guía para maestros/as- Matemática 20
Grado 99
Lección 2:
(4/12)
Objetivo:
Materiales:
Multipliquemos
• Construir la tabla del 5.
(N) habichuelas, tapitas, piedrecitas.
1. Leer el problema y captar
su sentido. [C]
M: ¿Cuál es la cantidad de gru-
pos y cuál es la cantidad en
cada grupo?
2. Escribir el PO. [C1]
3. Encontrar la cantidad total
de los tomates hasta el caso
de 4 canastas. [C2]
Que encuentren los productos
utilizando la adición sucesiva,
pero aprovechando el estudio
de la clase anterior, es decir,
que ellos se den cuenta de que
pueden encontrar el producto
sumando 5 al producto anterior.
* Se puede hacer que utilicen las
habichuelas, tapitas o piedreci-
tas para la confirmación.
4. Expresar el resultado y con-
firmar la respuesta del pro-
blema.
5. Analizar la forma en que au-
menta el producto. [C3]
M: Para llegar al producto de 5 x 5,
¿cuánto se necesita sumar al
producto de 5 x 4? ¿Por qué?
Que se den cuenta que se au-
menta de 5 en 5.
M: ¿Por qué los productos au-
mentan de 5 en 5?
RP: Porque hay 5 canastas y
cada canasta aumenta un
tomate en cada fila.
6. Encontrar los productos
hasta “5 x 9”. [C4]
* Después de escuchar los resul-
tados, concluir la característica
de la tabla del 5 (véase Notas).
7. Leer la tabla del 5. [C5]
Si hay niños y niñas que se dieron cuenta de otras ca-
racterísticas o formas de expresión, por ejemplo, “se
está haciendo en la forma de contar de 5 en 5”, “los nú-
meros de las unidades son 5, 0, 5, 0, ...”, felicitarles diciendo
que “están observando muy bien los números”, “descubrieron algo
muy interesante” etc. y hacer que los demás lo noten también.
C Hay 5 canastas, y hay 4 tomates en cada canasta.
¿Cuántos tomates hay en total?
1 Escriba el planteamiento de la operación.
2 Encuentre el total de tomates, paso a paso, hasta el caso de 4 tomates en cada
canasta.
5 x 4
73setenta y tres
3 Observe los productos de 5 x 1 a 5 x 4 y piense.
Planteamiento de la operación: 5 x 4 = 20 Respuesta: 20 tomates
5 x 1 1 + 1 + 1 + 1 + 1 5
(1)
Se necesita sumar 5. Porque los productos aumentan de 5 en 5.
(2)
Para llegar al producto de 5 x 5, ¿cuánto se necesita sumar al producto de
5 x 4? ¿Por qué?
Confirme el producto de 5 x 5 llenando la tabla.
4 Encuentre los productos de 5 x 6 a 5 x 9 llenando la tabla.
Los productos de la tabla del 5 aumentan de 5 en 5.
Se pueden encontrar sumando 5 al producto anterior.
5 Lea la tabla del 5.
Forma de encontrar el producto ProductoPlanteamiento
de la operación
5 x 2 2 + 2 + 2 + 2 + 2 10
5 x 3 3 + 3 + 3 + 3 + 3 15
5 x 4 20
(4/12)
4 + 4 + 4 + 4 + 4
5 x 5 255 + 5 + 5 + 5 + 5
5 x 6 306 + 6 + 6 + 6 + 6
5 x 7 357 + 7 + 7 + 7 + 7
5 x 8 408 + 8 + 8 + 8 + 8
5 x 9 459 + 9 + 9 + 9 + 9

119. Unidad 7 - Multiplicación100
MultipliquemosLección 2:
(5/12~6/12)
• Memorizar y aplicar la tabla del 5.
(M) tarjetas de la multiplicación
(N) tijeras, clip, sobre
Objetivo:
Materiales:
1. Captar el tema. [D]
2. Escribir la tabla del 5 y leer-
la. [D1]
* Dar la orientación general para
la memorización usando la ta-
bla escrita en la lámina.
3. Decir la tabla del 5 observan-
do la colección de pelotas.
[D2]
4. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [D3]
* Explicar el procedimiento nue-
vo de práctica (en pareja).
5. Seguir practicando la tabla de
modo que logre memorizar.
* Variar la forma de práctica de
modo que no se aburran.
6. Confirmar el estado de la me-
morización de la tabla del 5.
* Dar el tiempo para desafiar la
memorización.
7. Resolver los ejercicios del
3 al 5 .
La base del desarrollo de las clases de ahora en adelante es igual que las clases desarrolladas
con la tabla del 2. Por lo tanto se omiten algunas instrucciones para los maestros y las maestras,
por ejemplo, “se puede aprovechar el tiempo preparando la lámina de la tabla junto con los niños y
las niñas”, etc. Se debe seguir haciéndolo aunque no aparezca escrito para el mejor entendimiento en
los niños y las niñas.
En el LE se explican 2 ejemplos para la práctica con las tarjetas de la multiplicación. De ahora en adelante el maes-
tro o la maestra debe ir usando varias maneras para la práctica como se presenta en Columnas.
Planteamiento de la operación: ____________
D Vamos a practicar la tabla del 5.
3 Resuelva los siguientes ejercicios.
74 setenta y cuatro
1 Escriba la tabla del 5
y léala en orden.
2 Diga la tabla del 5 en orden observando la
colección de pelotas.
Tabla del 5
5 x 1 = 5
3 Haga las tarjetas de la multiplicación
y practique con ellas.
(1) (2) (3) (4) (5)
(6) (7) (8) (9)
5 x 3 = 5 x 6 = 5 x 4 = 5 x 9 = 5 x 7 =
5 x 2 = 5 x 1 = 5 x 5 = 5 x 8 =
4 Resuelva los siguientes problemas
(1) Hay 5 bolsas y en cada bolsa hay 4 naranjas. ¿Cuántas naranjas hay por todo?
(2) Hay 5 maestros. Cada maestro tiene 9 cuadernos. ¿Cuántos cuadernos hay por todo?
(3) Hay 5 flores con 6 pétalos cada una. ¿Cuántos pétalos hay en total?
En parejaIndividualmente
¡Cinco por
dos, diez!
¡Cinco por
cuatro, veinte!
Planteamiento de la operación: ____________
Planteamiento de la operación: ____________
Respuesta: ____________
Respuesta: ____________
5 Invente un problema de la multiplicación cuyo
planteamiento de la operación sea 5 x 3 y resuélvalo.
Dibuja la
situación del
problema.
Ya sabes cómo se
cubre la colección de
pelotas ¿verdad?
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
15 30 20 45 35
10 5 25 40
(5/12 ~ 6/12)
5 x 9 = 45
5 x 4 = 20 20 naranjas
5 x 9 = 45 45 cuadernos
5 x 6 = 30
Se omite la solución
Respuesta: ____________30 pétalos

120. Guía para maestros/as- Matemática 20
Grado 101
Lección 2:
(7/12)
Objetivo:
Materiales:
Multipliquemos
• Construir la tabla del 3.
(N) habichuelas, tapitas, piedrecitas.
1. Leer el problema y captar su
sentido. [E]
M: ¿Cuál es la cantidad de grupos y
cuál es la cantidad en cada grupo?
Que capten que la cantidad de
grupo es 3 (árboles) y la canti-
dad en cada grupo es 5 (aves).
* En este problema aparecen nú-
meros en el orden diferente que
el PO para que piensen bien en la
situación del problema. Hay que
orientar tomando en cuenta esta
dificultad.
2. Escribir el PO. [E1]
3. Encontrar la cantidad total
de aves hasta el caso de 5
aves en cada árbol. [E2]
Que encuentren los productos utili-
zando la adición sucesiva, pero apro-
vechando el estudio de la clase ante-
rior, es decir, que ellos se den cuenta
de que pueden encontrar el producto
sumando 3 al producto anterior.
* Se puede hacer que utilicen las
habichuelas, tapitas o piedrecitas
para la confirmación.
4. Expresar el resultado y confir-
mar la respuesta del problema.
5. Analizar la forma en que au-
menta el producto. [E3]
M: ¿Cómo se puede encontrar el
producto de 3 x 6 usando el
producto de 3 x 5? ¿Por qué?
Quesedencuentaquesepuede
encontrar sumando 3 porque los
productos aumentan de 3 en 3.
M: ¿Por qué los productos aumentan
de 3 en 3?
RP: Porque hay 3 árboles y cada ár-
bol aumenta un ave en cada fila.
6. Encontrar los productos has-
ta “3 x 9”. [E4]
* Después de escuchar los re-
sultados, concluir con la carac-
terística de la tabla del 3.
7. Leer la tabla del 3. [E5]
Cuando el estudio se continúa en la misma manera tras
largo tiempo, los niños y las niñas suelen volverse difíci-
les, al grado de aburrirse aunque estén jugando. Por lo
tanto es mejor variar la forma del ejercicio observando siem-
pre las circunstancias de los niños y las niñas para que puedan
mantenerse motivados.
75setenta y cinco
E Hay 3 árboles y hay 5 aves en cada árbol. ¿Cuántas aves hay en total?
1 Escriba el planteamiento de la operación.
2 Encuentre el total de aves paso a paso hasta el caso de 5 aves en cada árbol.
3 x 5
3 Encuentre el producto de 3 x 6 usando el producto de 3 x 5.
Planteamiento de la operación: 3 x 5 = 15 Respuesta: 15 aves
Planteamiento de la operación: 15 + 3 = 18 Respuesta: 18
4 Encuentre los productos de 3 x 6 a 3 x 9 llenando la tabla.
Los productos de la tabla del 3 aumentan de 3 en 3.
Se pueden encontrar sumando 3 al producto anterior.
5 Lea la tabla del 3.
Forma de encontrar el producto ProductoPlanteamiento
de la operación
(7/12)
3 x 1 1 + 1 + 1 3
3 x 2 2 + 2 + 2 6
3 x 3 3 + 3 + 3 9
3 x 4 124 + 4 + 4
3 x 5 155 + 5 + 5
3 x 6 186 + 6 + 6
3 x 7 217 + 7 + 7
3 x 8 248 + 8 + 8
3 x 9 279 + 9 + 9

121. Unidad 7 - Multiplicación102
MultipliquemosLección 2:
(8/12~9/12)
• Memorizar y aplicar la tabla del 3.
(M) tarjetas de la multiplicación
(N) tijeras, clip, sobre
Objetivo:
Materiales:
1. Captar el tema. [F]
2. Escribir la tabla del 3 y leer-
la. [F1]
* Dar la orientación general para
la memorización usando la ta-
bla escrita en la lámina.
3. Decir la tabla del 3 observan-
do la colección de pelotas.
[F2]
4. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [F3]
* Explicar el procedimiento nue-
vo de práctica.
5. Seguir practicando la tabla de
modo que logre memorizar.
* Variar la forma de práctica de
modo que no se aburran.
6. Confirmar el estado de la me-
morización de la tabla del 3.
* Dar el tiempo para desafiar la
memorización.
8. Resolver los ejercicios del
6 al 8 .
[Juego del Distraído]
1. El maestro o la maestra tendrá el papel de hacer las preguntas. Viendo al lado derecho dará
unas palmadas y después viendo al lado izquierdo dará otras palmadas.
2. Los niños y las niñas escucharán con concentración la cantidad de las palmadas. Y todos juntos darán las
palmadas de la cantidad del producto de la multiplicación de las palmadas dadas del lado derecho y del lado
izquierdo. (Por ejemplo, cuando el maestro o la maestra dé 3 palmadas al lado derecho y 4 al izquierdo, ellos
responderán con 12 palmadas.)
Continúa en la siguiente página…
76 setenta y seis
F Vamos a practicar la tabla del 3.
1 Escriba la tabla del 3
y léala en orden
2 Diga la tabla del 3 en orden
observando la colección de pelotas.
Tabla del 3
3 x 1 = 3
3 Haga las tarjetas de la multiplicación
y practique con ellas
6 Resuelva los siguientes ejercicios.
7 Resuelva los siguientes problemas.
8 Invente un problema cuyo planteamiento de la
operación sea 3 x 4 y resuélvalo.
(1) (2) (3) (4) (5)
(6) (7) (8) (9)
3 x 8 = 3 x 5 = 3 x 1 = 3 x 3 = 3 x 6 =
3 x 7 = 3 x 2 = 3 x 4 = 3 x 9 =
Sólo una tabla
Junto con las
tablas aprendidas
3 x 1
3 x 3
3 x 2
5 x 1 3 x 2
2 x 9
5 x 7
(1)
Planteamiento de la operación: ______________
(2)
Planteamiento de la operación: ______________
(3)
Si hay 3 bolsas y 5 galletas en cada bolsa. ¿Cuántas galletas hay por todo?
Hay 3 barcas y en cada barca hay 7 niños. ¿Cuántos niños hay en total?
Hay 3 niños y cada niño tiene 2 pesos. ¿Cuántos pesos tienen por todo?
Planteamiento de la operación: ______________
Respuesta: ____________
Respuesta: ____________
Respuesta: ____________
Representa la
situación del problema
con el dibujo.
Tres por tres,
nueve....
24 15 3 9 18
21 6 12 27
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
(8/12 ~ 9/12)
3 x 9 = 27
3 x 5 = 15
3 x 7 = 21
3 x 2 = 6
15 galletas
21 niños
6 centavos
Se omite la solución

122. Guía para maestros/as- Matemática 20
Grado 103
Lección 2:
(10/12)
Objetivo:
Materiales:
Multipliquemos
• Construir la tabla del 4.
(N) habichuelas, tapitas, piedrecitas.
1. Leer el problema y captar
su sentido. [G]
M: ¿Cuál es la cantidad de gru-
pos y cuál es la cantidad en
cada grupo?
Que capten que la cantidad de
grupo es 4 (cajas) y la cantidad
en cada grupo es 5 (pelotas).
2. Escribir el PO. [G1]
3. Encontrar la cantidad total de
las pelotas hasta el caso de 5
pelotas en cada caja. [G2]
Que encuentren los productos
utilizando la adición sucesiva,
pero aprovechando el estudio
de la clase anterior, es decir,
que ellos se den cuenta de
que pueden encontrar el pro-
ducto sumando 4 al producto
anterior.
* Se puede hacer que utilicen
los materiales concretos para
la confirmación.
4. Expresar el resultado y confir-
mar la respuesta del problema.
5. Analizar la forma en que au-
menta el producto. [G3]
M: ¿Cómo se puede encontrar el
producto de 4 x 6 usando el
producto de 4 x 5? ¿Por qué?
Quesedencuentaquesepuede
encontrar sumando 4 porque los
productos aumentan de 4 en 4.
M: ¿Por qué los productos au-
mentan de 4 en 4?
RP: Porque hay 4 cajas y cada caja
aumenta una pelota en cada fila.
6. Encontrar los productos has-
ta “4 x 9”. [G4]
* Después de escuchar los re-
sultados, concluir con la carac-
terística de la tabla del 4.
7. Leer la tabla del 4. [G5]
… viene de la página anterior
3. El niño o niña que dé la cantidad de palmadas distraídamente, tendrá
el papel de preguntar la siguiente vez.
4. Es mejor que la persona que hace la pregunta dé una señal para que
todos puedan dar las palmadas juntos.
* Los niños y las niñas estarán muy nerviosos por hacer dos cosas, escu-
char la cantidad de las palmadas y multiplicarlas. Por lo tanto hay que tener
cuidado de no continuar dando las preguntas con los números mayores.
G Hay 4 cajas que tienen 5 pelotas cada una.
¿Cuántas pelotas hay en total?
1 Escriba el planteamiento de la operación.
77setenta y siete
4 x 5
2 Encuentre el total de pelotas, paso a paso, hasta el caso de 5 pelotas en cada caja.
3 Encuentre el producto de 4 x 6 usando el producto de 4 x 5.
Planteamiento de la operación: 4 x 5 = 20 Respuesta: 20 pelotas.
Planteamiento de la operación: 20 + 4 = 24 Respuesta: 24
Los productos de la tabla del 4 aumentan de 4 en 4.
Se pueden encontrar sumando 4 al producto anterior.
4 Encuentre los productos de 4 x 6 a 4 x 9 llenando la tabla.
5 Lea la tabla del 5.
Forma de encontrar el producto ProductoPlanteamiento
de la operación
(10/12)
4 x 1 41 + 1 + 1 + 1
4 x 2 82 + 2 + 2 + 2
4 x 3 123 + 3 + 3 + 3
4 x 4 164 + 4 + 4 + 4
4 x 5 205 + 5 + 5 + 5
4 x 6 246 + 6 + 6 + 6
4 x 7 287 + 7 + 7 + 7
4 x 8 328 + 8 + 8 + 8
4 x 9 369 + 9 + 9 + 9

123. Unidad 7 - Multiplicación104
MultipliquemosLección 2:
(11/12~12/12)
• Memorizar y aplicar la tabla del 4.
(M) tarjetas de la multiplicación
(N) tijeras, clip, sobre
Objetivo:
Materiales:
1. Captar el tema. [H]
2. Escribir la tabla del 4 y leer-
la. [H1]
* Dar la orientación general para
la memorización usando la ta-
bla escrita en la lámina.
3. Decir la tabla del 4 observan-
do la colección de pelotas.
[H2]
4. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [H3]
* Explicar el procedimiento nue-
vo de práctica.
5. Seguir practicando la tabla de
modo que logre memorizar.
* Variar la forma de práctica de
modo que no se aburran.
6. Confirmar el estado de la me-
morización de la tabla del 4.
* Dar el tiempo para desafiar la
memorización.
7. Resolver los ejercicios del
9 al 11. Respuesta: ______________
Respuesta: ______________
Respuesta: ______________
H Vamos a practicar la tabla del 4.
78 setenta y ocho
1 Escriba la tabla del 4
y léala en orden.
2 Diga la tabla del 4 en orden
observando la colección de pelotas.
Tabla del 4
4 x 1 = 4
Planteamiento de la operación: ____________
Planteamiento de la operación: ____________
Planteamiento de la operación: ____________
3 Haga las tarjetas de la multiplicación
y practique con ellas.
9 Resuelva los siguientes ejercicios.
10 Resuelva los siguientes problemas.
(1)
(6)
(2) (3) (4) (5)
(7) (8) (9)
4 x 2 =
4 x 5 =
4 x 6 = 4 x 4 = 4 x 1 = 4 x 9 =
4 x 3 = 4 x 7 = 4 x 8 =
(1) Hay 4 gatos y cada gato tiene 2 orejas. ¿Cuántas orejas hay en total?
(2) Hay 4 cajas y en cada caja hay 5 camisetas. ¿Cuántas camisetas hay por todo?
(3) Compro 4 borradores que valen 8 pesos cada uno. ¿Cuánto cuestan en total?
1 Invente un problema cuyo planteamiento de la operación
sea uno de la tabla del 4 y resuélvalo
1
Voy a inventar usando
"4x6". ¿Y tú?
En equipo
¡12!
4x2 = 8
¡2x6 =12!
4x3 =12
..
.
8
20
24 16 4 36
12 28 32
4 x 2 = 8
4 x 2 = 8
4 x 5 = 20
4 x 8 = 32
4 x 3 = 12
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
8 orejas
20 camisetas
32 pesos
(11/12 ~ 12/12)
4 x 9 = 36
Se omite la solución

124. Guía para maestros/as- Matemática 20
Grado 105
Unidad 7:
(1/1)
Objetivo:
Materiales:
Ejercicios (1)
• Resolver los ejercicios y problemas de la aplicación
de las tablas del 2, 5, 3 y 4.
Los ejercicios tratan sobre:
1 Las tablas del 2, 5, 3 y 4
2 El sentido de la multiplica-
ción y la forma de hacer el
PO
* En el caso del inciso (1) no
se puede aplicar la multiplica-
ción. Hay que usar la suma.
3 Las multiplicaciones que
tienen el mismo producto
4 Problemas de aplicación
* Si hay niños y niñas que tie-
nen dificultades por no poder
entender la situación del pro-
blema o que no han podido
decir la tabla correctamente,
aconsejar que utilicen la co-
lección de pelotas o las habi-
chuelas, tapitas o piedrecitas
para que resuelvan los proble-
mas confirmando el sentido de
la multiplicación.
Es mejor empezar la clase con la práctica de las tablas
(por ejemplo, 3 minutos todos juntos y 10 minutos indi-
vidualmente) para recordarlas. Se puede aprovechar las
clases de los ejercicios para confirmar el estado de la memo-
rización de las tablas llamando a los niños y a las niñas uno por uno y
escuchando su desafío mientras los demás resuelven los ejercicios. En
ese caso, no hay que olvidar recorrer el aula para detectar las deficien-
cias y dar la orientación individual en la resolución de los ejercicios.
Respuesta: ________________
Respuesta: ________________
Respuesta: _____________
Planteamiento de la
operación: _____________
Respuesta: ____________
79setenta y nueve
Ejercicios (1)
1 Resuelva los siguientes ejercicios.
(1) 5 x 8 =
(5) 3 x 8 =
(9) 2 x 7 =
(13) 5 x 9 =
(17) 4 x 5 =
(2) 3 x 9 =
(6) 5 x 6 =
(10) 3 x 7 =
(14) 2 x 8 =
(18) 5 x 7 =
(3) 4 x 6 =
(7) 2 x 9 =
(11) 4 x 9 =
(15) 3 x 6 =
(19) 2 x 6 =
(4) 2 x 5 =
(8) 4 x 7 =
(12) 5 x 5 =
(16) 4 x 8 =
(20) 3 x 5 =
2 Resuelva cuántos objetos o elementos hay en cada caso
3 Una con la línea las tarjetas que tienen el mismo producto.
Planteamiento de la
operación: ____________
4 x 5
3 x 8
3 x 6 2 x 8 4 x 6 2 x 6
4 x 4 5 x 4 2 x 9 4 x 3
4 Resuelva los siguientes problemas.
Quiero comprar 2 galletas y una galleta cuesta 7 pesos. ¿Cuántos pesos necesito?
Están pasando 3 camiones. En cada camión van 5 barriles de agua. ¿Cuántos
barriles de agua van por todo?
Hay 5 bancas que caben 8 personas en cada una. ¿Cuántas personas pueden
sentarse en total?
(1) (2)
ROBOT
ROBOT
ROBOT
Respuesta: ___________
Planteamiento de la
operación: ___________
(3)
Respuesta: ________________Planteamiento de la operación: ____________
Planteamiento de la operación: ____________
Planteamiento de la operación: ____________
Compro 4 fundas y cada funda tiene 6 tortillas. ¿Cuántas tortillas tendré en total?
Respuesta: ________________Planteamiento de la operación: ____________
(1)
(2)
(3)
(4)
40
24
14
45
20
27
30
21
16
35
24
18
36
18
12
10
28
25
32
15
(1/1)
5 x 3 = 15
15 uvas9 robots
3 x 5 = 15
15 pescados
2 + 3 + 4 = 9
14 pesos2 x 7 = 14
40 personas5 x 8 = 40
15 barriles de agua3 x 5 = 15
24 tortillas4 x 6 = 24

125. Unidad 7 - Multiplicación106
Nos divertimosUnidad 7:
(No hay distribución de horas.)
[Nos divertirnos]
* Con esta actividad, se puede
profundizar en qué situación
se utiliza la multiplicación.
Motivar a los niños y las niñas
que busquen las circunstan-
cias donde se puede aplicar
la multiplicación en la vida co-
tidiana.
* En la ilustración aparecen las
situaciones donde se pueden
aplicar diferentes PO en la
misma situación, por ejemplo,
la cantidad de las botellas de
leche, se puede decir que es
3 x 4 y también 4 x 3. Mencio-
nar que hay casos como éste
donde el PO cambia depen-
diendo de cómo observa la
situación, o sea, dependiendo
de la agrupación (cuál es la
cantidad en cada grupo y cuál
es la cantidad de grupos).
3934450
3934450
Leche
Leche
Leche
Leche
Leche
Leche
Leche
Leche
Leche
Leche
Leche
Leche
80 ochenta
¿Donde está escondida la multiplicación?
Nos divertimos

126. Guía para maestros/as- Matemática 20
Grado 107
Lección 3:
(1/12)
Objetivo:
Materiales:
Sigamos multiplicando
• Construir la tabla del 6.
(N) habichuelas, tapitas, piedrecitas.
1. Leer el problema y captar
su sentido. [A]
M: ¿Cuál es la cantidad de grupos y
cuál es la cantidad en cada grupo?
Que capten que la cantidad de
grupos es 6 (platos) y la cantidad
en cada grupo es 4 (pasteles)
2. Escribir el PO. [A1]
3. Construir la tabla del 6. [A2]
Que encuentren los productos
sumando 6 al producto anterior.
* Se puede hacer que escriban
la forma de encontrar el pro-
ducto no de forma “6 + 6 + 6”
sino de “12 + 6” utilizando el
producto anterior dependien-
do de la situación de los niños
y las niñas.
* Se puede hacer que utilicen las
habichuelas, tapitas o piedrecitas
para la confirmación.
4. Encontrar la respuesta del
problema. [A3]
5. Analizar la forma en que au-
menta el producto. [A4]
M: Cuando se aumenta en 1 el
2do factor, ¿cuánto aumenta
el producto?
Que se den cuenta que cada
vez que el �����������������2do factor�������se au-
menta en 1, el producto au-
menta 6 (véase Notas).
* Concluir con la característica
de la tabla del 6.
6. Leer la tabla del 6. [A5]
Hasta ahora, los niños y las niñas analizaron la caracte-
rística de cada tabla desde el punto de vista “para llegar
al siguiente producto ¿cuánto se necesita sumar?”. En
esta clase, que ellos analicen desde el punto de vista de la
relación entre el 2do factor y el producto.
ochenta y uno 81
Lección 3: Sigamos Multiplicando
A Hay 6 platos y cada uno tiene 4 pasteles. ¿Cuántos pasteles hay en total?
1 Escriba el planteamiento de la operación.
6 x 4
4 Cuando se aumenta en 1 el 2do factor, ¿cuánto aumenta el producto?
5 Lea la tabla del 6.
En la tabla del 6, cuando el 2do factor
se aumenta en 1, el producto aumenta 6.
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
aumenta 6
aumenta 6aumenta 1
aumenta 1
2 Construya la tabla del 6 con la ayuda de la colección de pelotas.
3 Encuentre la respuesta.
Planteamiento
de la operación: 6 x 4 = 24
Respuesta: 24 pasteles
Forma de encontrar el producto ProductoPlanteamiento
de la operación
Se puede permitir que
escriban 12 + 6, 18 + 6,... etc.,
usando el producto anterior.
(1/12)
6 x 1 61 + 1 + 1 + 1 + 1 + 1
6 x 2 122 + 2 + 2 + 2 + 2 + 2
6 x 3 183 + 3 + 3 + 3 + 3 + 3
6 x 4 244 + 4 + 4 + 4 + 4 + 4
6 x 5 305 + 5 + 5 + 5 + 5 + 5
6 x 6 366 + 6 + 6 + 6 + 6 + 6
6 x 7 427 + 7 + 7 + 7 + 7 + 7
6 x 8 488 + 8 + 8 + 8 + 8 + 8
6 x 9 549 + 9 + 9 + 9 + 9 + 9

127. Unidad 7 - Multiplicación108
Sigamos multiplicando
• Memorizar y aplicar la tabla del 6.
(M) tarjetas de la multiplicación.
(N) tijeras, clip, sobre.
Objetivo:
Materiales:
1. Captar el tema. [B]
2. Escribir la tabla del 6 y leer-
la. [B1]
* Dar la orientación general para
la memorización usando la ta-
bla escrita en la lámina.
3. Decir la tabla del 6 observan-
do la colección de pelotas.
[B2]
4. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [B3]
5. Seguir practicando la tabla de
modo que logre memorizar.
* Variar la forma de práctica de
modo que no se aburran.
6. Confirmar el estado de la me-
morización de la tabla del 6.
* Dar el tiempo para desafiar la
memorización.
7. Resolver los ejercicios del
1 al 3 .
Lección 3:
(2/12~3/12)
82 ochenta y dos
B Vamos a practicar la tabla del 6.
1 Escriba la tabla del 6
y léala en orden.
2 Diga la tabla del 6 en orden
observando la colección de pelotas.
Tabla del 6
6 x 1 = 6
1 Resuelva los siguientes ejercicios.
2 Resuelva los siguientes problemas.
(1) 6 x 1 = (2) 6 x 3 = (3) 6 x 5 = (4) 6 x 7 =
(6) 6 x 9 = (7) 6 x 6 = (8) 6 x 4 = (9) 6 x 8 =
(5) 6 x 2 =
3 Invente un problema cuyo planteamiento de la operación sea uno de la tabla
del 6 y resuélvalo.
3 Haga las tarjetas de la multiplicación
y practique con ellas.
Hay 6 cajas. En cada caja hay 3 mangos. ¿Cuántos mangos hay en total?
Planteamiento de la operación: _____________
Una libra de sal cuesta 7 pesos. ¿Cuántos pesos necesito para comprar 6 libras?
En cada minibús van 8 personas. ¿Cuántas personas van en 6 minibuses?
Hay 6 escritorios con 4 gavetas cada uno. ¿Cuántas gavetas hay en total?
Respuesta: ______________
Planteamiento de la operación: _____________ Respuesta: ______________
Planteamiento de la operación: _____________ Respuesta: ______________
Planteamiento de la operación: _____________ Respuesta: ______________
(1)
(2)
(3)
(4)
6 x 8
6 x 4 6 x 2
6 x 9
6 x 5
6 x 7
6 x 1
6 x 3
No te olvides de practicar
más las tarjetas
en que te equivocaste.
6 x 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 18 30 42
54 36 24 48
12
(2/12 ~ 3/12)
6 x 9 = 54
Se omite la solución
6 x 3 = 18 18 mangos
6 x 7 = 42 42 pesos
6 x 8 = 48 48 personas
6 x 4 = 24 24 gavetas

128. Guía para maestros/as- Matemática 20
Grado 109
Lección 3:
(4/12)
Objetivo:
Materiales:
Sigamos multiplicando
• Construir la tabla del 7.
(N) habichuelas, tapitas, piedrecitas.
1. Leer el problema y captar su
sentido. [C]
M: ¿Cuál es la cantidad de gru-
pos y cuál es la cantidad en
cada grupo?
Que capten que la cantidad
de grupos es 7 (canastas) y la
cantidad en cada grupo es 5
(pelotas).
2. Escribir el PO. [C1]
3. Construir la tabla del 7. [C2]
Que encuentren los productos su-
mando 7 al producto anterior.
* Se puede hacer que escriban
la forma de encontrar el pro-
ducto no de forma “7 + 7 + 7”
sino de “14 + 7” utilizando el
producto anterior dependien-
do de la situación de los niños
y las niñas.
* Se puede hacer que utilicen las
habichuelas, piedrecitas o tapi-
tas para la confirmación.
4. Encontrar la respuesta del
problema. [C3]
5. Analizar la forma en que au-
menta el producto. [C4]
M: Cuando se aumenta en 1 el
2do factor, ¿cuánto aumenta
el producto?
Que se den cuenta que cada
vez que el 2do factor se aumen-
ta en 1, el producto aumenta 7.
* Concluir con la característica
de la tabla del 7.
6. Leer la tabla del 7. [C5]ochenta y tres 83
C Hay 7 canastas con 5 pelotas cada una. ¿Cuántas pelotas hay en total?
1 Escriba el planteamiento de la operación.
7 x 5
2 Construya la tabla del 7 con la ayuda de la colección de pelotas.
3 Encuentre la respuesta.
Planteamiento de la
operación: 7 x 5 = 35
Respuesta: 35 pelotas
4 Cuando se aumenta en 1 el 2do factor, ¿cuánto aumenta el producto?
En la tabla del 7, cuando
el 2do factor se aumenta
en 1, el producto aumenta 7.
5 Lea la tabla del .7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
aumenta 7
aumenta 7aumenta 1
aumenta 1
ProductoForma de encontrar el producto
Planteamiento
de la operación
(4/12)
7 x 1 71 + 1 + 1 + 1 + 1 + 1 + 1
7 x 2 142 + 2 + 2 + 2 + 2 + 2 + 2
7 x 3 213 + 3 + 3 + 3 + 3 + 3 + 3
7 x 4 284 + 4 + 4 + 4 + 4 + 4 + 4
7 x 5 355 + 5 + 5 + 5 + 5 + 5 + 5
7 x 6 426 + 6 + 6 + 6 + 6 + 6 + 6
7 x 7 497 + 7 + 7 + 7 + 7 + 7 + 7
7 x 8 568 + 8 + 8 + 8 + 8 + 8 + 8
7 x 9 639 + 9 + 9 + 9 + 9 + 9 + 9
Se puede permitir que
escriban 14 + 7, 21 + 7,... etc.,
usando el producto anterior.

129. Unidad 7 - Multiplicación110
Sigamos multiplicando
• Memorizar y aplicar la tabla del 7.
(M) tarjetas de la multiplicación
(N) tijeras, clip, sobre
Objetivo:
Materiales:
1. Captar el tema. [D]
2. Escribir la tabla del 7 y leer-
la. [D1]
* Dar la orientación general para
la memorización usando la ta-
bla escrita en la lámina.
3. Decir la tabla del 7 observan-
do la colección de pelotas.
[D2]
4. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [D3]
5. Seguir practicando la tabla
de modo que logre memori-
zar.
* Variar la forma de práctica de
modo que no se aburran.
6. Confirmar el estado de la me-
morización de la tabla del 7.
* Dar el tiempo para desafiar la
memorización.
7. Resolver los ejercicios del
4 al 6 .
De ahora en adelante aparece en los problemas las
cantidades continuas, por ejemplo, libras y pulgadas. Si
hay niños y niñas que demuestran dificultades en el uso
de estas unidades de magnitudes, dar la orientación indivi-
dual o grupal demostrando la situación del problema con los objetos
concretos para que ellos capten que si se puede aplicar la multiplica-
ción en cada situación respectiva.
Lección 3:
(5/12~6/12)
84 ochenta y cuatro
D Vamos a practicar la tabla del 7.
1 Escriba la tabla del 7
y léala en orden.
2 Diga la tabla del 7 en orden
observando la colección de pelotas.
3 Haga las tarjetas de la multiplicación
y practique con ellas.
3 x 7
4 x 9
2 x 6
7 x 2
Tabla del 7
7 x 1 = 7
4 Resuelva los siguientes ejercicios.
5 Resuelva los siguientes problemas.
(1) 7 x 4 = (2) 7 x 7 = (3) 7 x 9 = (4) 7 x 1 =
(6) 7 x 3 = (7) 7 x 5 = (8) 7 x 8 = (9) 7 x 6 =
(5) 7 x 2 =
Un borrador cuesta 4 pesos. ¿Cuántos pesos se necesita para comprar 7 borradores?
Planteamiento de la operación: _____________
Hay 7 manzanas y cada manzana cuesta 9 pesos ¿cuántos pesos necesito
para comprar las 7 manzanas?
Hay 7 niños y cada niño tiene 6 pelotas. ¿Cuántas pelotas hay en total?
Hay 7 cajas con 8 latas de jalea cada una. ¿Cuántas latas de jalea hay en total?
6 Invente un problema cuyo planteamiento de la operación sea uno de la tabla del 7 y resuélvalo.
Respuesta: ______________
Planteamiento de la operación: _____________ Respuesta: ______________
Planteamiento de la operación: _____________ Respuesta: ______________
Planteamiento de la operación: _____________ Respuesta: ______________
(1)
(2)
(3)
(4)
2 x 2
5 x 3
5 x 4
7 x 4
Ya tengo varias
tarjetas
(5/12 ~ 6/12)
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
28 49 63 7
21 35 56 42
14
7 x 4 = 28 28 pesos
7 x 9 = 63 63 pesos
7 x 6 = 48 42 pelotas
7 x 8 = 56 42 latas de jalea
Se omite la solución

130. Guía para maestros/as- Matemática 20
Grado 111
Lección 3:
(7/12)
Objetivo:
Materiales:
Sigamos multiplicando
• Construir la tabla del 8.
(N) habichuelas, tapitas, piedrecitas.
1. Leer el problema y captar
su sentido. [E]
M: ¿Cuál es la cantidad de gru-
pos y cuál es la cantidad en
cada grupo?
Que capten que la cantidad
de grupos es 8 (bancas) y la
cantidad en cada grupo es 4
(niños).
2. Escribir el PO. [E1]
3. Pensar en la característica
de la tabla del 8. [E2]
M: Cuando se aumenta en 1 el
2do factor, ¿cuánto aumenta
el producto?
Que se den cuenta que cada
vez que el ��������������������2do factor����������se aumen-
ta en 1, el producto aumenta 8.
* Concluir con la característica
de la tabla del 8.
4. Construir la tabla del 8. [E3]
Que encuentren los productos
sumando 8 al producto ante-
rior (véase Notas).
* Se puede hacer que utilicen las
habichuelas, tapitas o piedrecitas
para la confirmación.
5. Encontrar la respuesta del
problema. [E4]
6. Leer la tabla del 8. [E5]
Durante esta actividad, que los niños y las niñas sientan
la ventaja o la conveniencia, por ejemplo: se puede cal-
cular fácilmente o se puede encontrar el producto fácil-
mente, etc., a través de notar la forma característica en que
aumentan ordenadamente, siguiendo la regla.
ochenta y cinco 85
E 4 niños pueden sentarse en cada banca.
Si hay 8 bancas, ¿cuántos niños pueden sentarse en total?
1 Escriba el planteamiento de la operación. 8 x 4
2 Cuando se aumenta en 1 el 2do factor, ¿cuánto aumentará el producto en la
tabla del 8?
En la tabla del 6. se aumenta 6.
En la del 7, se aumenta 7.
Entonces en la tabla del 8,
se aumentará 8.
3 Construya la tabla del 8 usando lo descubierto y confirme
el producto con la ayuda de la colección de pelotas.
4 Encuentre la respuesta.
Planteamiento de la
operación: 8 x 4 = 32
Respuesta: 32 niños
8 x 2 = 16
8 x 3 = 24
aumenta 1 aumenta 8
5 Lea la tabla del 8.
1 2 3 41 2 3 4
1 2 3 41 2 3 4
1 2 3 41 2 3 4
1 2 3 41 2 3 4
Forma de encontrar el producto
8 x 1
Producto
881 + 1 + 1 + 1 + 1 + 1 + 1 + 1
Planteamiento
de la operación
(7/12)
8 x 2
8 x 3
8 x 4
8 x 5
8 x 6
8 x 7
8 x 8
8 x 9
16
24
32
40
48
56
64
72
2 + 2 + 2 + 2 + 2 + 2 + 2 + 2
3 + 3 + 3 + 3 + 3 + 3 + 3 + 3
4 + 4 + 4 + 4 + 4 + 4 + 4 + 4
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5
6 + 6 + 6 + 6 + 6 + 6 + 6 + 6
7 + 7 + 7 + 7 + 7 + 7 + 7 + 7
8 + 8 + 8 + 8 + 8 + 8 + 8 + 8
9 + 9 + 9 + 9 + 9 + 9 + 9 + 9
8 + 8
16 + 8
24 + 8
32 + 8
40 + 8
48 + 8
56 + 8
64 + 8

131. Unidad 7 - Multiplicación112
Sigamos multiplicando
• Memorizar y aplicar la tabla del 8.
(M) tarjetas de la multiplicación
(N) tijeras, clip, sobre
Objetivo:
Materiales:
1. Captar el tema. [F]
2. Escribir la tabla del 8 y leer-
la. [F1]
* Dar la orientación general para
la memorización usando la ta-
bla escrita en la lámina.
3. Decir la tabla del 8 observan-
do la colección de pelotas.
[F2]
4. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [F3]
5. Seguir practicando la tabla de
modo que logre memorizar.
* Variar la forma de práctica de
modo que no se aburran.
6. Confirmar el estado de la me-
morización de la tabla del 8.
* Dar el tiempo para desafiar la
memorización.
7. Resolver los ejercicios del
7 al 9 .
Lección 3:
(8/12~9/12)
F Vamos a practicar la tabla del 8.
Tabla del 8
8 x 1 = 8
1 Escriba la tabla del 8
y léala en orden.
2 Diga la tabla del 8 en orden
observando la colección de pelotas.
86 ochenta y seis
3 Haga las tarjetas de la multiplicación y
practique con ellas.
7 Resuelva los siguientes ejercicios.
8 Resuelva los siguientes problemas.
(1) 8 x 5 = (2) 8 x 4 = (3) 8 x 3 = (4) 8 x 7 =
(6) 8 x 1 = (7) 8 x 2 = (8) 8 x 6 = (9) 8 x 8 =
(5) 8 x 9 =
A cada persona se le entrega 5 pulgadas de cinta. ¿Cuántas pulgadas de cinta
necesita para 8 personas?
Planteamiento de la operación: _____________
Hay 8 fundas con 7 galletas cada una. ¿Cuántas galletas hay en total?
De un papel se hacen 9 tarjetas para la invitación de cumpleaños. ¿Cuántas
tarjetas se pueden hacer con 8 papeles?
Se forman grupos con 6 niños y niñas cada uno y quieren formar 8 grupos.
¿Cuántos niños y niñas se necesitan?
9 Invente un problema cuyo planteamiento de la operación sea uno de la tabla
del 8 y resuélvalo.
Respuesta: _______________
Planteamiento de la operación: _____________ Respuesta: _______________
Planteamiento de la operación: _____________ Respuesta: _______________
Planteamiento de la operación: _____________ Respuesta: _______________
(1)
(2)
(3)
(4)
¿Te ha ido bien
en la memorización
de la tabla de la
multiplicación?
40 32 24 56
8 16 48 64
72
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40
8 x 6 = 48
8 x 7 = 56
8 x 8 = 64
8 x 9 = 72
(8/12 ~ 9/12)
8 x 5 = 40 40 pulgadas de cinta
8 x 7 = 56 56 galletas
8 x 9 = 72 72 tarjetas
8 x 6 = 48 48 niños y niñas
Se omite la solución

132. Guía para maestros/as- Matemática 20
Grado 113
Lección 3:
(10/12)
Objetivo:
Materiales:
Sigamos multiplicando
• Construir la tabla del 9.
(N) habichuelas, tapitas, piedrecitas.
1. Leer el problema y captar
su sentido. [G]
M: ¿Cuál es la cantidad de gru-
pos y cuál es la cantidad en
cada grupo?
Que capten que cantidad de
grupos es 9 (hojas) �����������y ���������la canti-
dad en cada grupo es 5 (calco-
manías).
2. Escribir el PO. [G1]
3. Pensar en la característica
de la tabla del 9. [G2]
M: Cuando se aumenta en 1 el
2do factor, ¿cuánto aumenta
el producto?
Que se den cuenta que cada
vez que el �����������������2do factor�������se au-
menta en 1, el producto aumen-
ta 9.
* Concluir con la característica
de la tabla del 9.
4. Construir la tabla del 9. [G3]
Que encuentren los productos
sumando 9 al producto anterior.
* Se puede hacer que utilicen las
habichuelas, tapitas o piedrecitas
para la confirmación.
5. Encontrar la respuesta del
problema. [G4]
6. Leer la tabla del 9. [G5]
Al observar los productos de la tabla del 9 (9, 18, 27,
36,...), los dígitos de las unidades disminuyen de 1 en
1, en cambio los dígitos de las decenas aumenta de 1 en
1. También, la suma de los dos dígitos es 9. Si hay niños o
niñas que se dieron cuenta de estas características, felicitarles por
su actitud de estudiar con mucho interés. (En cuanto a este contenido
se tratará en la lección 5.)
G Compré 9 hojas de calcomanías. Cada hoja lleva 5 calcomanías.
¿Cuántas calcomanías tengo en total?
1 Escriba el planteamiento de la operación.
2 Cuando se aumenta en 1 el 2do factor, ¿cuánto aumentará el producto en la
tabla del 9?
9 x 5
Se aumentará 9
3 Construya la tabla del 9 usando lo descubierto y confirme el producto con
la ayuda de la colección de pelotas.
4 Encuentre la respuesta
Planteamiento de la
operación: 9 x 5 = 45
9 x 1 9 9
Respuesta: 45 calcomanías
5 Lea la tabla del 9.
ochenta y siete 87
¡Qué fácil es encontrar
el producto con
esta característica de
la tabla de la multiplicación!
9 x 1 = 9
9 x 2 = 18
aumenta 9aumenta 1
Forma de encontrar el producto ProductoPlanteamiento
de la operación
9 x 2 9 + 9 18
9 x 3 18 + 9 27
9 x 4 27 + 9 36
9 x 5 36 + 9 45
9 x 6 45 + 9 54
9 x 7 54 + 9 63
9 x 8 63 + 9 72
9 x 9 72 + 9 81
(10/12)

133. Unidad 7 - Multiplicación114
Sigamos multiplicandoLección 3:
(11/12~12/12)
• Memorizar y aplicar la tabla del 9.
(M) tarjetas de la multiplicación
(N) tijeras, clip, sobre
Objetivo:
Materiales:
1. Captar el tema. [H]
2. Escribir la tabla del 9 y leer-
la. [H1]
* Dar la orientación general para
la memorización usando la ta-
bla escrita en la lámina.
3. Decir la tabla del 9 observan-
do la colección de pelotas.
[H2]
4. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [H3]
5. Seguir practicando la tabla
de modo que logre memori-
zar.
* Variar la forma de práctica de
modo que no se aburran.
6. Confirmar el estado de la me-
morización de la tabla del 9.
* Dar el tiempo para desafiar la
memorización.
7. Resolver los ejercicios del
10 al 12.
88 ochenta y ocho
H Vamos a practicar la tabla del 9.
1 Escriba la tabla del 9
y léala en orden.
2 Diga la tabla del 9 en orden
observando la colección de pelotas.
Tabla del 9
9 x 1 = 9
3 Haga las tarjetas de la multiplicación
y practique con ellas.
9
x
2
9 x 5
9 x 8
63
81
10 Resuelva los siguientes ejercicios.
11 Resuelva los siguientes problemas.
(1) 9 x 4 = (2) 9 x 7 = (3) 9 x 9 = (4) 9 x 8 =
(6) 9 x 3 = (7) 9 x 6 = (8) 9 x 2 = (9) 9 x 5 =
(5) 9 x 1 =
12 Invente un problema cuyo planteamiento de la operación sea uno de la tabla del 9 y resuélvalo.
Cada caja pesa 6 libras. Si hay 9 cajas, ¿cuántas libras pesan en total?
Planteamiento de la operación: _____________
Leo 4 páginas de un libro cada día. ¿Cuántas páginas leo en 9 días?
Respuesta: ______________
Planteamiento de la operación: _____________ Respuesta: ______________
(1)
(2)
(3)
(4)
Quiero comprar 9 bolígrafos. Cada bolígrafo vale 7 pesos. ¿Cuántos pesos necesito?
Hay 9 niños y niñas. Si se reparten 8 mentas a cada uno, ¿cuántas mentas se
necesitan por todo?
Planteamiento de la operación: _____________ Respuesta: ______________
Planteamiento de la operación: _____________ Respuesta: ______________
36 63 81 72
27 54 18 45
9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
(11/12 ~ 12/12)
9 x 9 = 81
9 x 6 = 54 54 libras
9 x 4 = 36 36 páginas
Se omite la solución
9 x 7 = 63 63 pesos
9 x 8 = 72 72 mentas

134. Guía para maestros/as- Matemática 20
Grado 115
Unidad 7:
(1/1)
Objetivo:
Materiales:
Ejercicios (2)
• Resolver los ejercicios y problemas de la aplicación
de las tablas del 6 al 9.
Los ejercicios tratan sobre:
1 Las tablas del 6 al 9
2 Encontrar el PO conocien-
do el producto de las ta-
blas del 6 al 9
3 El sentido de la multiplica-
ción y la forma de hacer el
PO
4 Problemas de aplicación
* Los incisos (3) y (4) son los
problemas donde los núme-
ros aparecen en el diferente
orden que el PO.
* Si hay niños y niñas que tie-
nen dificultades por no poder
entender la situación del pro-
blema o que no han podido
decir la tabla correctamente,
aconsejar que utilicen la co-
lección de pelotas o las habi-
chuelas, tapitas o piedrecitas
para que resuelvan los pro-
blemas confirmando el senti-
do de la multiplicación.
Planteamiento de
la operación: ____________
Respuesta: ____________Respuesta: ____________
Planteamiento de
la operación: ____________
Respuesta: ____________
ochenta y nueve 89
1 Resuelva los siguientes ejercicios.
Ejercicios (2)
(1) 6 x 6 = (2) 7 x 9 = (3) 9 x 5 = (4) 8 x 8 =
(5) 7 x 7 = (6) 6 x 8 = (7) 9 x 7 = (8) 8 x 9 =
(9) 8 x 7 = (10) 7 x 5 = (11) 6 x 7 = (12) 9 x 6 =
(13) 6 x 5 = (14) 8 x 6 = (15) 7 x 6 = (16) 9 x 9 =
(17) 9 x 8 = (18) 7 x 8 = (19) 8 x 5 = (20) 6 x 9 =
2 Encuentre con qué multiplicación resulta el producto indicado en cada tabla.
(1) Tabla del 6 (2) Tabla del 7 (3) Tabla del 8 (4) Tabla del 9
24 ( 21 ( 72 ( 63 (
54 ( 56 ( 32 ( 36 (
42 ( 28 ( 48 ( 45 (
x x x x
x x x x
x x x x
) ) ) )
) ) ) )
) ) ) )
3 Cuántos objetos hay en cada caso.
4 Resuelva los siguientes problemas.
Planteamiento de la operación: _____________ Respuesta: _____________
Planteamiento de la operación: _____________ Respuesta: _____________
Hay 6 jaibas en cada funda. Si hay 7 fundas, ¿cuántas jaibas hay en total?
Se venden papas a 8 pesos la libra. ¿Cuántos pesos cuestan 7 libras?
Planteamiento de la operación: _____________ Respuesta: _____________
Planteamiento de la operación: _____________ Respuesta: _____________
Necesito 9 alambres que midan 7 pulgadas cada uno. ¿Cuántas pulgadas de
alambre necesito en total?
Durante 8 semanas, he ahorrado 7 pesos por semana. ¿Cuántos pesos tengo en ahorro?
(1)
(1)
(2)
(3)
(4)
Planteamiento de
la operación: ____________
(2) (3)
9 colores9 colores 9 colores9 colores 9 colores9 colores 9 colores9 colores
9 colores9 colores 9 colores9 colores 9 colores9 colores 9 colores9 colores
36 63 45 64
49 48 63 72
56 35 42 54
30 48 42 81
72 56 40 54
6 7 8 9
6 7 8 9
6 7 8 9
4 3 9 7
9 8 4 4
7 4 6 5
6 x 6 = 36 8 x 9 = 72
36 estampillas 72 lápices
7 x 6 = 42 42 jaibas
7 x 8 = 56 56 pesos
9 x 7 = 63 63 pulgadas
8 x 7 = 56 56 pesos
7 x 5 = 35
35 manzanas
(1/1)

135. Unidad 7 - Multiplicación116
Multipliquemos con 1
• Construir y memorizar la tabla del 1.Objetivo:
Materiales:
1. Leer el problema y captar su
sentido. [A]
M: ¿Cuántas pelotas hay en cada
caja y cuántos cajas hay?
2. Encontrar la respuesta
pensando paso a paso des-
de el caso que hay más de
una caja. [A1]
M: ¿Cómo sería el PO si hay 3
cajas? ¿Si hay 2 cajas?
M: En este problema, ¿cuál es la
cantidad de grupos y cuál es
la cantidad en cada grupo?
Que se den cuenta que se pue-
de usar la multiplicación aun-
que la cantidad de grupo es 1.
3. Construir la tabla del 1 y pen-
sar en su característica. [A2]
M: Cuando se aumenta en 1 el
2do factor, ¿cuánto aumenta
el producto?
M: ¿Hay algo que notaron obser-
vando el 2do factor y el pro-
ducto?
Que se den cuenta que los pro-
ductos son iguales a los facto-
res, como diferencia particular
con las otras tablas.
4. Investigar los productos de
la multiplicación con 1. [A3]
M: ¿Hay algo que notaron obser-
vando los productos de la mul-
tiplicación con 1?
RP: El producto es igual al primer
factor.
* Concluir con la característica
de la multiplicación con 1.
5. Hacer las tarjetas de la mul-
tiplicación y practicar con
ellas. [A4]
6. Resolver los ejercicios 1 y 2 .
En la vida cotidiana es raro encontrar la situación de usar
la tabla del 1 (se usa cuando se multiplican los números de
2 cifras, por ejemplo, 28 x 31).
Lección 4:
(1/1)
Planteamiento de la operación: ____________ Respuesta: ___________
Planteamiento de la operación: ____________ Respuesta: ___________
Lección 4: Multipliquemos con 1
90 noventa
A Hay 4 pelotas en cada caja. Si hay 1 caja, ¿cuántas pelotas hay en total?
1 Piense paso a paso desde el caso que hay más de una caja.
Planteamiento de la
operación: 1 x 4 = 4
Respuesta: 4 pelotas
Construya la tabla del 1 con la ayuda
de la colección de pelotas.
32 Observe la tabla del 1 y la multiplica-
ción con 1 de otras tablas y piense la
característica.
2 x 1 = 2
1 x 1 = 1
3 x 1 = 3
4 x 1 = 4
5 x 1 = 5
6 x 1 = 6
7 x 1 = 7
8 x 1 = 8
9 x 1 = 9
Cualquier número multiplicado
con 1 es igual al mismo número.
4 Haga las tarjetas de la multiplicación
y practique con ellas.
1 Resuelva los siguientes ejercicios.
La cantidad de
grupos es 1
¿verdad?
2 Resuelva los siguientes problemas.
(1) 1 x 8 = (2) 1 x 2 = (3) 1 x 5 = (5) 1 x 3 =
(6) 1 x 6 = (7) 1 x 7 = (8) 1 x 4 = (9) 1 x 1 =
(1) Hay 1 funda y cada una tiene 7 sandías, ¿cuántas sandías hay en total?
(4) 1 x 9 =
(2) Cada niña tiene 8 mentas. Si hay 1 niña, ¿Cuántas mentas hay en total?
Producto
3 x 4 =
2 x 4 =
1 x 4 =
Planteamiento
de la operación
12
8
4
1 x 7 = 7 7 sandías
1 x 8 = 8 8 mentas
8 2 5 3
6 7 4 1
9
(1/1)
1 x 2
1 x 1
1 x 4
1 x 3
1 x 6
1 x 5
1 x 8
1 x 9
1 x 7
2
1
4
3
6
5
8
9
7

136. Guía para maestros/as- Matemática 20
Grado 117
Lección 5:
(1/3)
Objetivo:
Tabla de la multiplicación
• Construir y leer la tabla de dos dimensiones (doble
entrada) para la multiplicación.
1. Captar el tema. [A]
2. Observar la tabla y pensar
en la forma de construir lle-
nando las casillas de la ta-
bla del 2. [A1]
M: ¿Qué observan en esta tabla?
Que se den cuenta que hay
casillas del 1er factor y del
2do factor.
M: ¿Dónde vamos a escribir los
productos de la tabla del 2?
Que piensen en qué lugares
escriben los productos de la ta-
bla del 2 insinuándoles con los
primeros 4 productos escritas
en el LE.
* Indicar que completen la tabla
del 2.
* Se puede confirmar la forma
de llenar usando la tabla del 3.
3. Completar la tabla. [A2]
M: Vamos a escribir todos los pro-
ductos diciendo cada tabla.
* Se puede hacer que consulten
a las tablas del LE si no han
podido memorizarlas todavía.
4. Practicar la manera de leer
a tabla. [A3]
M: ¿Dónde está el producto de 5
x 4? Indiquen con el dedo.
* Hacer que practiquen pregun-
tando alternadamente en pa-
reja.
5. Encontrar los secretos de
la tabla. [A4]
M: ¿Hay algo que descubrieron
observando los productos de
la tabla?
Que se den cuenta de varias
reglas o secretos en la tabla
(véase Notas).
Se puede preguntar las reglas descubiertas durante la cons-
trucción de las tablas del 1 al 9, por ejemplo, en la tabla del
6 el producto aumenta de 6 en 6, etc. para confirmarlo en esta
tabla. También preguntando otras observaciones, los niños y las ni-
ñas descubrirán más, por ejemplo, hay productos que aparecen sólo 1 vez
y hay otros que aparecen 2 o más veces, las unidades del producto de la tabla
del 5 repiten 5, 0, 5, 0..., los productos se ven como la simetría por el eje incli-
nado, etc. Así se puede cultivar no sólo la habilidad sobre la tabla de la multipli-
cación sino también se puede enriquecer la percepción para los números.
Materiales: (M) 1 cartel de tabla para una pizarra, lápiz
1 2 3 4
2 2 4 6 8
1
3
5
Casillas del multiplica
Casillasdelmultiplicando
Por
X
1 2 3 4
3 6 9
5 1 20
4 4
noventa y uno 91
Lección 5: Tabla de la multiplicación
A Vamos a construir otro tipo de tabla de la multiplicación.
1 Observe la tabla y complete las casillas de la tabla del 2.
2 Complete todas las casillas de las otras tablas.
1 2 3 4 5 6 7 8 9
2 4 6 82
1
3
5
6
7
8
9
Casillas del segundo factor
Casillasdelprimerfactor
Por
3 Practique en pareja cómo leer la tabla señalando el producto con el dedo.
4 Encuentre varios secretos interesantes observando esta tabla.
¡Ocho!
Aqui está.¿4 x 2?
4
1 2 3 4 5 6 7 8 9
10 12 14 16 18
3 6 9 12 15 18 21 24 27
4 8 12 16 20 24 28 32 36
5 10 15 20 25 30 35 40 45
6 12 18 24 30 36 42 48 54
7 14 21 28 35 42 49 56 63
8 16 24 32 40 48 56 64 72
9 18 27 36 45 54 63 72 81
(1/3)

137. Unidad 7 - Multiplicación118
Tabla de la multiplicación
• Descubrir la relación entre el segundo factor y el pro-
ducto como la característica de la multiplicación.
Objetivo:
1. Captar el tema. [B]
2. Observar la tabla del 3 y pen-
sar en la forma de aumentar
el producto. [B1]
* Hacer que digan la tabla del 3.
M: Cuando aumenta en 1 el 2do
factor, ¿cuánto aumenta el
producto?
RP: Aumenta en 3.
M: ¿Por qué el producto aumenta
en 3 cuando el 2do factor au-
menta en 1?
* Indicar que expliquen la razón
con sus propias palabras.
3. Observar la tabla del 8 y pen-
sar en la forma de aumentar
el producto. [B2]
* Seguir el mismo procedimien-
to que la actividad anterior.
4. Investigar en las otras tablas.
[B3]
* Indicar que escojan las tablas
para investigar.
* Resumir el resultado de la in-
vestigación escuchando los
niños y las niñas.
5. Concluir con la característi-
ca de la multiplicación.
* Concluir que en la multiplica-
ción cuando se aumenta 1 al
2do factor en el producto au-
menta una vez la cantidad del
1er factor.
6. Resolver el ejercicio 1 .
Lección 5:
(2/3)
B Vamos a investigar con la tabla.
1 Observe la tabla del 3.
Cuando el 2do factor se aumenta en 1, ¿cuánto aumenta el producto?
3 6 9 12 15 18 21 24 27
2 Observe la tabla del 8.
Cuando el 2do factor se aumenta en 1, ¿cuánto aumenta el producto?
Aumenta en 3
Aumenta en 8
3 Investigue en las otras tablas también.
En la multiplicación, cuando se aumenta 1 al 2do factor,
en el producto aumenta 1 vez la cantidad del 1er factor.
1 Escriba en las casillas los números que corresponde.
92 noventa y dos
¡Qué interesante
la tabla de la
multiplicación!
3
(1)
.
(2) .
más que 3 x 7.(3)
(4) es 9 más que 9 x 3.
(5)
(6)
En la tabla del 7, cuando el 2do factor se aumenta en 1,
el producto aumenta en
La tabla cuyos productos aumentan de 5 en 5 es la tabla del
3 x 8 es
9 x
6 x 3 es 6 menos que 6 x
4 menos que 4 x 3 es x 2.
.
3 3 3 3 3 3 3 3
(2/3)
7
5
3
4
4
4
Materiales: (M) tirillas, carteles

138. Guía para maestros/as- Matemática 20
Grado 119
Lección 5:
(3/3)
Objetivo:
Materiales:
Tabla de la multiplicación
• Descubrir que da el mismo resultado al cambiar el
orden de los factores en una multiplicación.
• Descubrir la propiedad conmutativa de la multipli-
cación como una regla.
1. Captar el tema. [C]
2. Encontrar la multiplicación
que tiene el mismo produc-
to. [C1]
M: Vamos a encontrar la multipli-
cación donde el producto es
15 (21, 30).
Que encuentren observando
la tabla de dos dimensiones.
3. Analizar la razón por la que
el producto es lo mismo.
M: ¿Por qué el producto entre 3
x 5 y 5 x 3 es lo mismo?
* Indicar que utilicen las habi-
chuelas, tapitas, piedrecitas,
la colección de pelotas o la
tabla de la multiplicación se-
gún la necesidad.
* Asignar niños y niñas para que
expresen sus opiniones.
* Explicar que desde otro punto
de vista, el mismo grupo de
objetos de 3 x 5 puede ser la
representación del sentido de
5 x 3.
* Concluir con el uso de la regla
de la propiedad conmutativa
de la multiplicación sin usar el
término.
4. Encontrar las multiplicacio-
nes cuyo producto sea 24.
[C2]
Que se den cuenta que aun-
que sea un solo producto se
puede descomponer en va-
rios tipos de multiplicación.
5. Encontrar otras multiplica-
ciones que tienen el mismo
producto. [C3]
* Los productos se pueden des-
componer en 1 tipo, 2 tipos, 3
tipos o 4 tipos de multiplica-
ción. Se puede profundizar la
actividad buscando cada tipo
de producto.
6. Resolver los ejercicios 2 y 3 .
[Actividad suplementaria]
Rompecabezas de la tabla de la multiplicación
1. Agrupar y encerrar hasta 5 productos de la tabla de la
multiplicación de modo que sean las mismas piezas.
2. Recortar cada pieza.
3. Reconstruir la tabla colocando las piezas correctamente. (Se puede
jugar intercambiando con el compañero o la compañera.)
(N) habichuelas, tapitas, piedrecitas.
noventa y tres 93
C Vamos a investigar más con la tabla.
1 Encuentre la multiplicación que da el mismo producto que las siguientes
multiplicaciones.
(1) 3 x 5 = 15
= 15
(2) 3 x 7 = 21 (3) 5 x 6 = 30
5 x 3 = 15 7 x 3 = 21 6 x 5 = 30
5 x 3 = 3 x 5 7 x 3 = 3 x 7 6 x 5 = 5 x 6
En la multiplicación, aunque cambie la posición de los factores
se tiene el mismo resultado.
2 Encuentre las multiplicaciones cuyo producto sea 24.
3 x 8, 8 x 3, 4 x 6, 6 x 4
3 Encuentre otras multiplicaciones cuyo producto sea igual.
2 Una con la línea las multiplicaciones que tienen el mismo producto.
3 Escriba las multiplicaciones cuyos productos sean los siguientes.
(1) 12 ( )
(2) 16 ( )
3 x 5 5 x 4 7 x 9 2 x 7 8 x 6 4 x 8
6 x 89 x 78 x 45 x 37 x 24 x 5
Hay 4 tipos de multiplicación
que da el mismo producto 24.
¡Qué interesante!
= 21x x x = 303 3 55 7 6
2 x 6, 3 x 4, 4 x 3, 6 x 2
2 x 8, 4 x 4, 8 x 2
(3/3)

139. Unidad 7 - Multiplicación120
Ejercicios (3)
• Resolver los ejercicios y problemas de la aplicación
de la multiplicación.
Objetivo:
Materiales:
Los ejercicios tratan sobre:
1 Ejercicios de las tablas de
la multiplicación
2 Las características y las
reglas de la multiplicación
3 El sentido y la forma de
hacer el PO de la multipli-
cación
4 Problemas de aplicación
Continúa en la siguiente página…
Unidad 7:
(1/2~2/2)
(N) lápices de color, tarjetas numerales
Respuesta: ____________Planteamiento de la operación: ____________
Respuesta: ____________Planteamiento de la operación: ____________
Respuesta: ____________Planteamiento de la operación: ____________
Respuesta: ____________Planteamiento de la operación: ____________
Planteamiento
de la operación: ____________
Respuesta: ____________
94 noventa y cuatro
Ejercicios (3)
1 Resuelva los siguientes ejercicios.
(3) 3 x 4 = (4) 5 x 7 =
(8) 6 x 2 = (9) 4 x 4 =
(13) 1 x 7 = (14) 4 x 3 =
(1) 1 x 4 =
(6) 9 x 4 =
(11) 5 x 3 =
(16) 3 x 8 =
(2) 7 x 8 =
(7) 2 x 7 =
(12) 6 x 9 =
(17) 9 x 7 = (18) 8 x 6 = (19) 2 x 9 =
(5) 6 x 4 =
(10) 8 x 9 =
(15) 7 x 6 =
(20) 4 x 8 =
2 Escriba en los cuadros el número que corresponde.
(1) 8 x 6 es más que 8 x 5.
(2) En la tabla del los productos aumentan de 4 en 4.
(3) 9 x 3 = x
(4) 1 x 8, , yx x x dan el mismo producto 8.
3 Encuentre cuántos guineos hay.
4 Resuelva los siguientes problemas.
(1) En una bolsa hay 7 mentas. Si hay 6 bolsas, ¿cuántos mentas hay en total?
(2) Tengo en las manos 2 diccionarios que pesan 4 libras cada uno.
¿Cuántas libras pesan en total?
(3) Si en cada mesa hay 8 invitados, ¿cuántos invitados hay en 3 mesas?
(4) A 5 hermanos les regalaron 7 pelotas a cada uno.
¿Cuántas pelotas les regalaron en total?
12 35
12 16
7 12
4
36
15
24
56
14
54
63 48 18
24
72
42
32
8
4
3 9
(1/2 ~ 2/2)
2 4 84 2 1
4 x 6 = 24
6 x 7 = 42 42 mentas
2 x 4 = 8 8 libras
3 x 8 = 24 24 invitados
5 x 7 = 35 35 pelotas
24 guineos

140. Guía para maestros/as- Matemática 20
Grado 121
Unidad 7:
(1/2~2/2)
Ejercicios (3) … viene de la página anterior
5 Construcción del problema
de la multiplicación
6 Ejercicios de las tablas de
la multiplicación
* Se puede hacer que inventen
el mismo tipo de ejercicio.
[Instrucciones (para la prácti-
ca de la tabla del 2)]
1. Dibujar la figura preferida.
2. Escribir en cada espacio los
productos de la tabla del 2.
3. Agregar más líneas de modo
que no se capten qué es el di-
bujo.
4. Escribir en otros espacios
los números que no son los
productos de la tabla del 2.
Continúa en la siguiente página…
[Continuación]
noventa y cinco 95
5 Invente un problema de la multiplicación.
Dibuje la situación del problema y resuélvalo.
Planteamiento de la operación:
Respuesta:
8x1
1x86x2
8x6
4x6
6x6
6x8
3x8
2x4
4x2 2x6
6x4
8x6
3x8
9x4
6x8
4x9
3x7
9x1
7x7
7x9
5x6
1x1
9x7
5x5
5x8
8x8 5x82x3
3x1 5x5
8 12 24 36 48
6 Pinte el siguiente dibujo con el color indicado según el producto.
Problema
Dibujo
rojo azul amarillo verde morado
Producto
Se omite la solución
Se omite la
solución

141. Unidad 7 - Multiplicación122
Ejercicios (3)Unidad 7:
(1/2~2/2)
… viene de la página anterior
7 Ejercicios de las tablas de
la multiplicación (del 7 al
9)
8 Ejercicios de las tablas de
la multiplicación
[Continuación]
96 noventa y seis
7 Haga el siguiente ejercicio siguiendo las instrucciones.
1.
2.
3.
4.
Escriba los productos de cada multiplicación.
Busque el número en el cuadro que es igual al producto de cada inciso.
Trace la línea uniendo los puntos que corresponde al producto siguiendo el orden
de cada inciso.
Pinte el dibujo formado por la línea con sus colores preferidos.
(2) (3) (4)
(6) (7) (8)
(10) 8 x 6 = (11) (12)
(1)
(5)
(9)
(13) (14) (15) (16)
8 x 9 = 8 x 2 = 7 x 3 = 7 x 4 =
9 x 7 = 9 x 4 = 8 x 7 = 9 x 6 =
8 x 3 = 7 x 2 = 7 x 6 =
9 x 5 = 7 x 5 = 9 x 3 = 9 x 8 =
8 Juegue en pareja.
1.
2.
3.
4.
5.
6.
Preparar las tarjetas numerales
(de 1 a 9, son 9 tarjetas).
Mezclar bien las tarjetas y
colocarlas con la cara hacia abajo.
Sacar dos tarjetas en orden
del grupo de tarjetas.
Multiplicar los dos números que
salieron.
El que tiene el producto mayor
recibe las tarjetas.
El que tiene más tarjetas gana.
17
14
48
40
25
24
54
49
42
56
71
33
37
36
63
28
29
21 23
14
16
72
41
45 44
35
34
27
22
16
21
!Gane!
<Instrucciones del juego>
Salida
72 16 21 28
63 36 56 54
24 48 14 42
45 35 27 72

142. Guía para maestros/as- Matemática 20
Grado 123
Unidad 7: Nos divertimos
(No hay distribución de horas)
[Nos divertimos]
* Se presenta un juego para
desarrollar el ejercicio de las
tablas de la multiplicación.
[Variedad del desarrollo del
juego del Bingo]
A: Escribir en las casillas co-
rrespondientes 9 productos
escogidos entre 2 tablas de la
multiplicación y que pregun-
ten también dentro de esas 2
tablas.
B: Escribir en las casillas los
PO y que pregunten dicien-
do los productos para que
encuentren el PO correspon-
diente al producto dicho.
C: Aumentar la cantidad de
las casillas hasta 16, o sea 4
columnas y 4 filas y realizar el
juego con la combinación de
2 tablas de la multiplicación.
[Intentémoslo]
(No hay distribución de horas)
* Esta actividad sirve para en-
contrar la característica de los
números del producto de cada
tabla. También se puede diver-
tir con la figura que se forma
por las líneas trazadas.
noventa y siete 97
1. En pareja decidir con qué tabla se
jugará.
2. Preparar las tarjetas de multiplicación
de la tabla decidida y dibujar en el
cuaderno 9 casillas.
3. Escribir los productos de la tabla
decidida en cada casilla que le guste
diciendo esa tabla.
4. Escoger alternadamente una tarjeta
con los ojos cerrados.
5. Decir el PO y el producto de la
tarjeta escogida y encerrar
el producto escrito en la casilla.
6. Repetir esta actividad y cuando
tengan 3 círculos en la forma
vertical, horizontal o inclinada,
decir "¡Bingo!" y gana.
28
7
21 14
35 49 28
63 7 56
144221
7 49 63
42 14 21
562835
35 49 28
63 7 56
144221
7 49 63
42 14 21
562835
¡BINGO!¡BINGO!
Yo
primero
Intentémoslo
Vamos a unir con la línea los número
que aparecen en la posición de las
unidades de cada producto de la tabla
del 7.
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
Hagámoslo en las otras tablas.
Nos divertimos
Juego del bingo de la multiplicación
Vamos a jugar
con la tabla del 7.
7 x 8
0
1
4
5
3
2
6
7
8
9
1
0
1
4
5
3
2
6
7
8
9
2
0
1
4
5
3
2
6
7
8
9
3
0
1
4
5
3
2
6
7
8
9
4
0
1
4
5
3
2
6
7
8
9
5
0
1
4
5
3
2
6
7
8
9
6
0
1
4
5
3
2
6
7
8
9
0
1
4
5
3
2
6
7
8
9
8
0
1
4
5
3
2
6
7
8
9
97
Primero pon tu lápiz en
el 0 y empieza a trazar
la línea. Al final, termina
regresando al 0.
No hay distribución de horas

143. Unidad 8 - Longitud124
8
• Aplican las unidades de centímetro, decímetro y metro del sistema métrico decimal en la medición de longitudes.
• Miden la longitud de objetos de su entorno con una regla graduada y cinta métrica.
• Estiman longitudes usando las unidades de metro, decímetro y centímetro.
Longitud
Expectativas de logro
(8 horas)Unidad
1
8
1/6 • Necesidad y utilidad de las unidades oficiales
3 Plan de estudio (8 horas)
1. Midamos en metros, decíme
tros y centímetros
(6 horas) 2/6 • Construcción de la regla de 1 metro
• Unidad oficial del sistema métrico decimal “el metro”
• Medición de la longitud usando “el metro”
3/6 • Unidades oficiales del sistema métrico decimal “el
centímetro” y “el decímetro”
• Relación entre las unidades oficiales (1 dm = 10 cm)
4/6 • Medición de la longitud usando “el centímetro”
5/6 • Uso de la medición para trazar línea recta
• Relación entre las unidades oficiales
(1 m = 10 dm, 1 m = 100 cm)
Longitud
• Unidad oficial del siste-
ma métrico: “km”.
• Medición de distancias
usando “km”.
• Relación entre las
unidades oficiales de
longitud: “km” y ”m”.
• Forma de escribir
longitud con notación
decimal.
• Adición y sustracción de
valores de longitud.
• Cálculo vertical de
valores de longitud con
notación decimal.
• Unidades oficiales de
longitud del sistema
inglés: “pulgada”, ”pié” y
”yarda”.
• Medición de longitudes
usando unidades oficia-
les del sistema inglés.
Longitud
• Unidades oficiales de
longitud del sistema mé-
trico: “m”, “dm” y “cm”.
• Medición de longitudes
usando unidades oficia-
les.
• Relación entre las
unidades oficiales de
longitud: “m”, “dm” y
“cm”.
• Estimación de longitu-
des.
Longitud
• Unidad oficial de longi-
tud del sistema métrico:
“mm”.
• Medición de longitudes
usando unidad oficial
“mm”.
• Relación entre las
unidades oficiales de
longitud: “m”, ”dm”, ”cm”
y ”mm”.
Longitud
• Comparación de longi-
tudes en forma directa.
• Comparación de longitu-
des en forma indirecta.
• Comparación de
longitudes utilizando
unidades arbitrarias.
Relación y desarrollo2

144. Guía para maestros/as- Matemática 20
Grado 125
Puntos de lección
• Lección 1: Midamos en metros, de-
címetros y centímetros
En 1er grado los niños y las niñas aprendie-
ron a medir utilizando las unidades de medida
arbitraria (corporales) después de tener la ex-
periencia de comparar la longitud de los ob-
jetos directa e indirectamente. De acuerdo a
esto, que los niños y las niñas se den cuenta
que, al utilizar las unidades de medida arbi-
traria (corporales), el tamaño de la unidad no
está bien definido pues ese tamaño depende
de las personas y se obtienen diferentes re-
sultados de la medición.
Así basándose en la necesidad de tener una
unidad fija, se introducen las unidades oficia-
les el “metro (m)”, el “centímetro (cm)” y el
“decímetro (dm)”. Los niños y las niñas harán
una cinta cuya longitud es de un metro, 10
grupos de 10 centímetros para que puedan
comprender la relación de “1 m = 10 dm = 100
cm” a través de la actividad de medir con la
cinta la longitud de los objetos concretos.
Las unidades de longitud se utilizan también
para expresar la distancia. Es muy probable
que en la actividad de medición surja la situa-
ción donde los niños y las niñas miden la dis-
tancia. Por lo tanto se puede usar el término
“distancia” pero dando más importancia a “la
longitud” para que los niños y las niñas capten
bien el sentido de la longitud.
En la unidad 6 “Figuras geométricas”, los ni-
ños y las niñas aprendieron el uso de la regla
pero sin medición. Aquí se explica su uso con
medición.
• Lección 2: Estimemos longitud
Aquí es que los niños pueden afianzar la uni-
dad de medida a utilizar de acuerdo a la longi-
tud a medir, para que se fije en ellos el tama-
ño del metro, del decímetro y del centímetro;
que comprendan la relación que existe entre
el tamaño de la longitud a medir y la unidad a
utilizar en la medición.
4
Hay que ubicar la regla justo en la parte inferior de la línea u objeto que
se quiere medir. Es importante alinear la marca del “0” de la escala de la
regla con el extremo de la línea y objeto. (Dibujo A)
No es necesario colocar siempre la marca del “0” al extremo de la línea u
objeto, sino que se puede empezar a medir desde cualquier marca pre-
ferida de la regla. Para este caso es necesario contar las marcas de la
escala de la regla de un extremo al otro de la línea u objeto, o calcular la
medición, como por ejemplo 9 – 2 = 7 centímetros. (Dibujo B)
Como este último procedimiento es más complicado, es recomendable,
para los niños y las niñas, empezar a medir desde la marca del “0” en el
extremo de la línea u objeto. Pero es mejor que se acostumbren poco a
poco a medir desde cualquier marca.
La forma de medir con la regla
6/6 • Escritura de la longitud usando la tabla de posición
de unidades (m, dm y cm)
• Medición de la longitud con las unidades oficiales
1/12. Estimemos longitud
(1 hora)
• Estimación de la longitud usando el metro, decí-
metro y centímetro
1/1 Ejercicios (1 hora) • Ejercicios
B
A
Columnas

145. Unidad 8 - Longitud126
Midamos en metros, decímetros y
centímetros
Lección 1:
(1/6)
• Conocer la unidad de medida oficial “el metro”.
(M) regla de 1 m
Objetivo:
Materiales:
5 Desarrollo de
clases
1. Captar el tema. [A]
* Explicar que la medida de
abrir los brazos se llama bra-
zada.
2. Pensar en el resultado de la
comparación. [A1]
M: ¿La pizarra B es más larga
que A? ¿Por qué?
Que capten que no se puede
concluir, porque la brazada en-
tre ellos puede ser diferente.
3. Medir la longitud de pizarra
con la brazada.
* Asignar niños y niñas para
que midan la pizarra con la
brazada de modo que salga
varios resultados.
4. Comparar la longitud de la
brazada. [A2]
* Concluir que la longitud de la
unidad de medida corporal cam-
bia según la persona que mide.
* Se puede confirmar con otras
unidades corporales (cuarta,
paso, etc.)
Que sientan la necesidad de
utilizar las unidades oficiales.
5. Conocer la unidad oficial
“el metro”.
M: ¿Cómo se puede llegar al
mismo resultado? ¿Qué ne-
cesitamos?
* Mostrar la regla de 1 m e infor-
mar que una unidad oficial es
“el metro” y se escribe “m”.
6. Conocer que 3 veces 1 me-
tro es 3 metros. [A3]
* Medir realmente la pizarra
con la regla de 1 m (véase
Notas) y confirmar que cual-
quiera puede llegar al mismo
resultado.
7. Resolver el ejercicio 1 .
[Importancia de la estimación]
En el estudio de la medida y la medición, uno de los ob-
jetos es que los niños y las niñas tengan la percepción de
la cantidad. Para eso es importante que estimen la cantidad antes
de medir. Es recomendable preguntar cuántos metros medirá más o
menos antes de cada medición.
Lección 1: Midamos en metros, decímetros y centímetros
Unidad 8
A Juan y Cintia midieron la longitud de las pizarras A y B .
98 noventa y ocho
Longitud
1 ¿Se puede decir que la pizarra B es más larga que A ? ¿Por qué?
3 La pizarra A mide 3 veces 1 metro. ¿Cómo se dice esta longitud?
Recordemos
1. ¿Cuál es más largo? 2. Una con la línea la unidad corporal y su nombre.
A
B
cuartapie pulgada
A Juan B Cintia
2 brazadas 2 brazadas y un poco más
2 Compare la longitud de una brazada entre compañeros y compañeras.
No. Porque la brazada de Juan y Cintia pueden ser diferentes.
Mi brazada es
más larga que
la tuya.
Es necesario
que todos usen algo
que tiene la misma
medida ¿verdad?
1 Escriba las siguientes longitudes con el número y el símbolo.
(1) Un metro (2) Dos metros (3) Catorce metros (4) Veinte metros
Una de las unidades oficiales para medir la longitud se llama metro.
El metro se escribe "m".
Juan
3 veces 1 metro se dice tres metros (3 m).
(1/6)
1 m 2 m 14 m 20 m

146. Guía para maestros/as- Matemática 20
Grado 127
Lección 1:
(2/6)
Objetivo:
Materiales:
• Construir una cinta de un metro y medir los objetos
del entorno con ella.
(M) regla de 1 m
(N) tijeras, pegamento
[Sabías que...]
La información suplementaria del metro
* Es recomendable preparar anticipadamente varios ti-
pos de metros para mostrarlos.
* Solicitar traer los recortes para cons-
truir el metro.
1. Captar el tema. [B]
M: Vamos a hacer la cinta de 1 m.
2. Construir la cinta de 1 m.
* Dirigir las tarjetas recortadas para
formar el metro.
* Comparar con la regla de 1 m y con-
firmar que la cinta construida mide 1
m.
3. Captar la longitud aproximada de 1
m.
M: ¿Qué tamaño tiene 1 m más o me-
nos?
* Hacer que abran los brazos de modo
que sea 1 m comparando con la cin-
ta. (aquí se puede hacer con un jue-
go del que estime mejor), se llaman
a 5 niños(as) para que pongan su
marca estimada de 1 metro y el que
esté más cerca es el ganador.
M: Vamos a trazar en la pizarra la línea
que mida más o menos 1 m.
* Asignar a algunos niños y niñas que
trace la línea en la pizarra y después
comparar con la cinta.
M: ¿Qué cosas podemos medir con “el
metro”?
Que se den cuenta que se usa para
medir la longitud larga.
4. Medir los objetos del entorno con
la cinta de 1 m.
M: Vamos a buscar si hay algo que mida
1 m en el alrededor.
* Indicar que estimen la longitud del
objeto antes de medir.
* Es mejor hacer que registren en el
cuaderno lo que midieron. Se pue-
de decir la parte que no llega a 1 m
como “un poco más” etc.
* Se puede hacer que trabajen en pa-
reja o equipo.
5. Expresar lo encontrado.
* Aprovechar las expresiones para
que los niños y las niñas sientan la
necesidad de tener otra unidad para
expresar la parte que no llega a 1 m.
99noventa y nueve
B Vamos a hacer una cinta de 1 m y midamos con ella.
Unirlas con el pegamento.
Recortar 10 tarjetas (pegadas de 2 en 2) de la página para recortar.
1 m
Registra en tu
cuaderno el objeto
y su longitud que
mediste.
¿Podrás encontrar
algo que mida 1 m?
Sabías que...
Al instrumento que se utiliza para medir también se le llama "metro".
Hay varias representaciones del metro:
Metro utilizado en las tiendas
Metro utilizado por el carpintero
Metro utilizado por el albañil
Metro utilizado por la costurera
1 m y un
poco más. Falta un
poco para
1 m.
1
2
(2/6)
Midamos en metros, decímetros y
centímetros

147. Unidad 8 - Longitud128
Lección 1:
(3/6)
• Conocer la unidad de medida oficial “el centímetro” y
el “decímetro”.
(M) regla, dibujo de mayor escala de la regla
Objetivo:
Materiales:
1. Captar el tema. [C]
* Recordar la actividad de me-
dir con la cinta de 1 m.
2. Conocer la unidad oficial
“el centímetro”. [C1]
M: ¿Qué necesita para saber la
longitud de “un poco más”?
* Mostrar una regla e informar
sobre “el centímetro” y su
símbolo.
M: ¿Qué parte del cuerpo tiene
más o menos 1 cm?
* Hacer que comparen la an-
chura del dedo etc. con 1 cm
representada en el LE para
que capten la longitud aproxi-
mada de 1 cm.
M: ¿Qué cosas podemos medir
con el centímetro?
Quecaptenqueseusaparame-
dir las longitudes no tan largas.
3. Conocer la forma de medir
con la regla usando el cen-
tímetro. [C2]
* Mostrar en la pizarra el dibujo
de mayor escala de la regla con
las medidas en centímetros y
explicar que la longitud “de 0 a
1”, “de 1 a 2”... se llama “1 cm”.
M: ¿Cuántas veces de 1 cm hay
en la cinta verde?
M: ¿Cómo diríamos esta longitud?
* Presentar otros ejercicios de
leer la regla usando el dibujo
de mayor escala de la regla.
4. Conocer la unidad oficial
“el decímetro”. [C3]
* Explicar sobre “el decímetro”,
su símbolo y la relación de “1
dm = 10 cm” (véase Notas).
M: ¿Qué parte del cuerpo tiene
más o menos 1 dm?
Que capten la longitud aproxi-
mada de 1 dm.
5. Resolver el ejercicio 2 .
Normalmente cuando se miden los objetos no se usa
la unidad decímetro sino que metro y centímetro. Para
evitar la confusión de los niños y las niñas, aquí se trata
el decímetro brevemente.
Midamos en metros, decímetros y
centímetros
100 cien
C La pizarra de la clase de Jacinto midió 2 m y un poco más.
1 m 1 m
1 ¿Qué necesita para medir la longitud que es menos que 1 m?
2 La longitud se puede medir con la regla.
Necesita la unidad más pequeña que 1 m.
Una unidad oficial de longitud que es menor que
1m se llama centímetro. El centímetro se escribe "cm".
¿Cuántos centímetros mide la cinta verde?
Cuando hay 10 cm, a esta longitud se le llama decímetro.
El decímetro se escribe "dm". 1 dm = 10 cm
La cinta tiene 6 veces 1 cm. Mide 6 cm.
10 cm
2 Escriba en la línea el número que corresponde.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
(cm)
3 ¿Cuántos centímetros mide la cinta azul?
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
(cm)
(1) La longitud que es 7 veces 1 cm es cm.
(2) 1 dm equivale a cm.
(3) La cinta rosada mide cm.
(4) La cinta amarilla mide cm.
(cm)0 1 2 3 4 5 6 7 8
(cm)
1 cm
7
10
2
8
(3/6)

148. Guía para maestros/as- Matemática 20
Grado 129
Lección 1:
(4/6)
Objetivo:
Materiales:
• Medir la longitud de los objetos del entorno usando la
regla y trazar líneas rectas con medición.
(M) regla
(N) regla, tijeras
1. Captar el tema. [D]
2. Hacer la regla en centíme-
tro. [D1]
* Si los niños y las niñas tienen
la regla, puede usarla sin ne-
cesidad de recortar la página
para recortar.
3. Medir con la regla los obje-
tos del entorno. [D2]
M: Vamos a medir la longitud del
ancho del LE. ¿Cómo hay
que colocar la regla?
Que capten que hay que co-
locar la regla justo abajo de la
parte que se quiere medir.
* Explicar la forma de medir la
longitud (véase Columnas).
* Si surgen longitudes menores
que 1 cm, expresar como “un
poco más” etc.
* Confirmar que cuando se usa
la unidad oficial resulta lo mis-
mo sin importar quien mida.
M: Vamos a medir las cosas del
entorno con la regla.
* Es mejor indicar que midan a
partir de la escala de 0 de la re-
gla para facilitar la medición.
4. Trazar la línea de 5 cm. [E]
* Explicar la forma de trazar la
línea con medición siguiendo
las instrucciones del LE.
* Se puede hacer que dividan en
centímetros la línea trazada.
* Indicar que practiquen trazar
las líneas de cierta longitud
dada aprovechando las líneas
trazadas en el cuaderno.
5. Resolver los ejercicios 3 y 4 .Cuando se miden los objetos que no se puede colocar
la regla bien pegada desde un extremo hasta otro extre-
mo, como por ejemplo, los lápices, sirve trazar la línea
auxiliar. Aunque es difícil trazarla correctamente para los ni-
ños y las niñas, se puede informar la utilidad de ella.
línea auxiliar
Midamos en metros, decímetros y
centímetros
D Vamos a medir la longitud usando centímetros.
1 Recorte la regla en centímetro de la página para recortar.
2 Mida la longitud de los objetos con ella.
4 Trace la línea de las siguientes longitudes.
E Vamos a trazar la línea de 5 cm con la regla.
1 Poner el punto inicial.
2 Contar 5 cm desde el
punto inicial y poner el
punto del otro extremo.
3 Unir dos puntos con la línea.
101ciento uno
(1) 3 cm
(2) 6 cm
(3) 11 cm
(4) 14 cm
Línea de 5 cm
(Punto inicial)
Tiene que colocar
bien la regla
3 Mida la longitud.
(1)
(2)
(3)
(4)
3 Mida la longitud.
CHICLECHICLE
(5)
(6)
Borrador
Se representa el punto inicial
(final) con el tamaño grande
para la mejor visualización.
En realidad
puede ser
más
pequeño
Si hay parte que es menor que 1 cm, se puede decir
como “un poco más” etc.
(4/6)
6 cm
8 cm
10 cm
12 cm
Se omite la solución
Se omite la solución
3 cm
4 cm

149. Unidad 8 - Longitud130
Lección 1:
(5/6)
• Conocer la relación entre las unidades de medida “1
m = 10 dm” y “1 m = 100 cm” y representar la longitud
en la tabla de posición de unidades (cm, dm, m).
(M) regla, dibujo de mayor escala de la regla
(N) cinta de 1 m, regla
Objetivo:
Materiales:
1. Captar el tema. [F]
M: ¿Cuántos centímetros medi-
rá una pizarra de 3 m 40 cm?
¿Qué necesita saber?
RP: Necesita saber cuántos centí-
metros mide 1 m.
2. Medir la cinta de 1 m y cono-
cer la relación entre m, dm y
cm. [F1]
M: Vamos a investigar cuántos cen-
tímetros mide la cinta de 1 m.
* Después de dar el tiempo para
la investigación individual, es-
cuchar el resultado.
RP: Midiendo toda la cinta con la
regla, sabemos que mide 100
cm. 1 tarjeta mide 10 cm y tiene
10 tarjetas, entonces contando
de 10 en 10 sabemos que mide
100 cm.
* Aprovechando las expresiones
de los niños y las niñas, concluir
la relación de “1 m = 100 cm” y
“1 m = 10 dm”.
3. Confirmar que 1 m equivale a
100 cm haciendo las marcas
de centímetros en la cinta. [F2]
4, Convertir metros en centíme-
tros y viceversa. [F3]
M: Entonces, ¿a cuántos centí-
metros equivale 3 m 40 cm?
RP: 3 m es igual a 300 cm, y 40 cm
más. 340 cm.
M: Se puede usar la tabla de las
unidades (m, dm y cm) para
representar la longitud y para
saber la equivalencia.
* Explicar la forma de escribir la
longitud en la tabla y la forma
de leer con diferentes unidades,
usando metros y centímetros, o
usando solamente centímetros
(véase Notas). En este caso, se
puede leer “tres metros cuaren-
ta centímetros” y también “tres-
cientos cuarenta centímetros”.
5. Resolver el ejercicio 5 .
Continúa en la siguiente página…
Generalmente, para decir la longitud de algún objeto,
no se usa la unidad “decímetro”. Por lo tanto, aquí se
orienta la lectura de la longitud escrita en la tabla, usan-
do solamente las unidades “m” y “cm”. Por la misma razón,
y también para evitar la confusión de los niños y las niñas, en la
tabla se escribe “dm” entre paréntesis y se usa el color diferente entre
m y cm para facilitar la lectura. La conversión entre dm y m se trata
brevemente.
Midamos en metros, decímetros y
centímetros
102 ciento dos
F Una pizarra mide 3 m 40 cm. ¿Cuánto mide si se usan centímetros?
1 Mida una tarjeta de la cinta de 1 m y piense cuántos centímetros hay en 1 m.
1 m equivale a 10 tarjetas de 10 cm (1 dm). 1 m = 10 dm
1 m = 100 cm
cm
cm
2 Haga las marcas de centímetros en la cinta de 1m y confirme si hay 100 cm.
3 ¿A cuántos centímetros equivale 3 m 40 cm?
3 m equivale a 300 cm.
Entonces 3 m 40 cm equivale a 340 cm.
Se puede usar la tabla de las unidades (m, dm y cm) para representar la longitud y
para saber la equivalencia.
3 m 40 cm
metros (decímetros) centímetros
Representa que es 340cm
Se parece a la
tabla de valores.
5 Escriba en la línea el número que corresponde.
(1) 1 m = ________dm (2) 1 m = ________cm (3) 4 m = ________dm
(4) 3 m = ________cm (5) 50 dm = ________m (6) 700 cm = ________m
Representa que es 2 m 5 cm
205 cm
1 m equivale a 100 cm.
3 4 0
2 0 5
10
300
100
5
40
7
(5/6)

150. Guía para maestros/as- Matemática 20
Grado 131
[Hasta aquí 5/6]
[Desde aquí 6/6]
Lección 1:
(6/6)
Objetivo:
Materiales:
• Medir los objetos del entorno usando metros y centí-
metros.
(N) cinta de 1 m, regla
… viene de la página anterior
6. Resolver el ejercicio 6 .
1. Captar el tema. [G]
M: Vamos a medir la longitud de
varios objetos del entorno.
2. Medir la longitud de los ob-
jetos del entorno.
* Indicar que estimen la longi-
tud antes de medir y registren
el resultado en el cuaderno.
* Se puede hacer que trabajen
en pareja o en equipo y tam-
bién se puede realizar esta
actividad fuera del aula.
* Es importante que ellos usen
el instrumento adecuado para
la medición, el metro o el cen-
tímetro, dependiendo del ob-
jeto que miden.
3. Expresar el resultado.
* Pedir varias experiencias para
medir correctamente, no sólo
las ideas buenas sino las difi-
cultades o problemas encon-
trados durante la actividad para
que tengan ganas de aprove-
char las experiencias de sus
compañeros y compañeras y
para que tengan interés por la
medición.
4. Resolver el ejercicio 7 .
Midamos en metros, decímetros y
centímetros
= ___________cm = ___________cm = ___________cm
Objetos
Longitud
1. El largo de la pizarra
2. El ancho del pupitre
3 m 48 cm
50 cm
103ciento tres
6 Represente las siguientes longitudes en la tabla de las unidades (m, dm, cm) y
escriba en la línea el número que corresponde.
(1) 2 m 15 cm (2) 9 m 30 cm (3) 6 m 8 cm
(4) 472 cm (5) 510 cm (6) 703 cm
= m cm = m cm = m cm
G Vamos a medir la longitud usando
metros y centímetros. Estima la longitud
antes de medir y registra
el resultado en tu cuaderno.
7 Escriba en el cuadro la unidad adecuada (cm o m).
(1) (2) (3)
(4) (5) (6)
3
15
3
8
50
27
2 1
215 930 608
5 9 3 0 6 0 8
4 7 2 5 1 0 7 0 3
cm
cm
cm
m
m
m
(6/6)
4 72 5 10 7 3

151. Unidad 8 - Longitud132
Estimemos longitudLección 2:
(1/1)
• Estimar longitud usando el metro, decímetro y centí-
metro.
Objetivo:
Materiales:
1. Leer el problema y captar
su sentido. [A]
* Presentar la situación del pro-
blema señalando dónde se va a
estimar.
M: Observar el largo de la piza-
rra y estimar su longitud.
Que se den cuenta que pue-
den usar la observación para
estimar su longitud y con qué
unidad de medida conviene
hacer la estimación.
2. Estimar la longitud.
3. Medir cada longitud usando
la unidad de medida corres-
pondiente y comparar los
resultados con la estima-
ción hecha.
* Dar tiempo para que encuen-
tren su solución (grupal o indi-
vidual).
4. Resolver el ejercicio 1 .
La estimación facilita que el niño y la niña tengan una
idea preliminar de la longitud de la cinta y esto le permite
a ellos saber la unidad de medida a usar cuando miden
longitud. Por otro lado, esta actividad se puede realizar como
un juego, poniendo a un grupo de estudiantes a que hagan sus esti-
maciones y que luego gane el que esté más cerca de las medidas reales,
es decir, el que haga las mejores estimaciones (También se puede hacer
el juego en grupo de 3 ó 4 niños y niñas).
(N) cinta de diferentes longitudes, metro, regla. (Pue-
den ser construídos con cartulina)
104 ciento cuatro
Lección 2: Estimemos longitud
A Estima cada una de las longitudes indicadas a continuación y luego
comprueba realizando la medición con la unidad adecuada.
1 Estimar la longitud de otros objetos del entorno como: el largo y el ancho
de la puerta del aula, el largo y el ancho de la cancha de baloncesto y
volibol, si hay; el largo del más alto del curso y del más bajo. Luego tomar
sus medidas y compararlas con las estimaciones.
Estimación Medida correcta
(1)
(2)
(3)
(4)
Largo de la pizarra
Ancho del CT
Longitud de un lápiz
Largo del aula
____________ ____________
____________ ____________
____________ ____________
____________ ____________
Estimar la longitud es tener el tamaño
aproximado metalmente sin medir.
Como...
dos metros
(1/1)
Se omite la solución

152. Guía para maestros/as- Matemática 20
Grado 133
Los ejercicios tratan sobre:
1 La relación entre las unida-
des oficiales de la longitud
2 La medición de la longitud
con la regla
3 El trazo de la línea recta
cuya medida dada
4 La selección de las unida-
des apropiadas
Continúa en la siguiente página…
EjerciciosUnidad 8:
(1/1)
• Resolver los ejercicios y problemas de aplicación con
las unidades de longitud.
Objetivo:
Materiales: (N) regla
( ) ( )
( )
(1) 300cm = m (2) 263cm = m cm
(3) 4m = cm (4) 1m 23cm = cm
(5) 2dm = cm (6) 50cm = dm
(7) 3m = dm (8) 70dm = m
1 Escriba en el cuadro el número que corresponde.
2 Mida la longitud de cada cinta.
3 Trace la línea de las siguientes longitudes.
4 Escriba en el cuadro la unidad adecuada (cm o m).
Ejercicios
(1)
(2)
(1) 8 cm
(2) 13 cm
(3) 4 cm
(1) (2) (3)
15
2
30
(3)
105ciento cinco
3
400
20 5
30
12 cm
9 cm
5 cm
cm
m
cm
Se omite la solución
7
123
2 63
(1/1)

153. Unidad 9 - Estadística134
Puntos de lección
• Lección 1: Recoleccionemos y organi-
cemos datos en tablas
En esta lección se expresa la colección, orga-
nización, distribución e interpretación de datos
en forma de tablas sencillas, arreglándolos y
clasificándolos para facilitar su lectura o inter-
pretación. Para ello el maestro o la maestra
debe usar los objetos o las situaciones que
están en el ambiente y en la vida cotidiana de
los niños y de las niñas haciéndoles sentir que
• Recopilan y clasifican datos proporcionados previamente.
• Organizan y distribuyen datos estadísticos en tablas o cuadros.
• Interpretan pictogramas.
Expectativas de logro
al expresarlos en la tabla se facilita captar la
característica general de los datos y la relación
entre las cantidades, por ejemplo la diferencia.
• Lección 2: Interpretemos pictogramas
En esta lección lo importante es la expresión de
datos usando gráficas y la pictografía es una
gráfica con coloridos que va a comparar datos
e informaciones usando símbolos y dibujos.
1
4
9
Estadística (2 horas)Unidad
9
1/1 • Recolección de datos
3 Plan de estudio (2 horas)
1. Recoleccionemos y organice
mos datos en tablas
(1 hora)
1/12. Interpretemos pictogramas
(1 hora)
• Interpretación de pictogramas
• Clasificación, conteo y organización de datos
• Distribución de datos en una tabla
Gráficas de barras
• Construcción e inter-
pretación de gráfica de
barras.
• Elaboración e interpre-
tación de tabla de dos
dimensiones.
Estadística
• Recolección, organi-
zación distribución e
interpretación de datos
en tablas.
• Interpretación de picto-
grama.
Tablas y gráficos esta-
dísticos
• Elaboración de pictogra-
ma.
• Elaboración e interpre-
tación de tabla de dos
dimensiones.
Relación y desarrollo2

154. Guía para maestros/as- Matemática 20
Grado 135
Forma de contar correctamente la cantidad de los elementos dibujados
A: Usando habichuelas, tapitas o piedrecitas (u otros objetos concretos).
1. Colocar una habichuela uno por uno encima de cada pollito.
2. Después de colocar las habichuelas, tapitas o piedrecitas en todos los pollitos, los quitan, los
cuentan y los tabulan.
B: Tachando o encerrando el dibujo uno por uno cada vez que cuente
Las formas dichas son para contar según la clasificación de elementos. O sea, primero cuentan los
pollitos, después cuentan los perros, luego cuentan los gatos, así de este modo.
Hay otra forma que es contar sin importar la clasificación de elementos.
C: Escribiendo las rayitas.
1. Tachar el dibujo de cualquiera de los animales.
2. Escribir una rayita en el lugar correspondiente de ese animal en la tabla.
3. Tachar cualquier otro dibujo de los animales.
4. Hacer una rayita en el lugar correspondiente de ese animal en la tabla.
5. Seguir haciendo rayitas al contar los objetos.
Si se hacen las rayitas en grupo de 5, se pueden contar de 5 en 5. Esta forma sirve mucho en el caso
de recopilar los datos, por ejemplo, para la encuesta.
Procesos principales para el estudio de la estadística
Para desarrollar el estudio de la estadística, generalmente se toman las siguientes 5 etapas.
1. Captar el problema o el tema como su propio problema y tener el objetivo de la investigación.
2. Recopilar los datos según el objetivo de la investigación.
3. Clasificar y organizar los datos con el criterio adecuado para lograr el objetivo.
4. Expresar o representar los datos en la forma de las tablas o gráficas adecuadas para que sean com-
prensible.
5. Analizar el resultado en las tablas o gráficas y captar las características y/o la tendencia de los acon-
tecimientos.
Es necesario dar la importancia en la primera etapa para que los niños y las niñas puedan desarrollar
las siguientes etapas con su propia iniciativa.
Columnas
1
2

155. Unidad 9 - Estadística136
Recoleccionemos y organicemos
datos en tablas
Lección 1:
(1/1)
• Recolectar, clasificar, organizar, distribuir e interpre-
tar datos en la tabla.
Objetivo:
5 Desarrollo de
clases
(M) tapitas, papel, lápices de colores.
(N) habichuelas.
Materiales:
Unidad 9 Estadística
106 ciento seis
Lección 1: Recoleccionemos y organicemos datos en tablas
A Vamos a realizar una encuesta para decidir qué alimento llevar al paseo.
1 Escriba un palito por cada alimento nombrado.
2 ¿Cuál es el alimento que más gusta?
Pizza
Alimentos CantidadConteo
Palitos de queso
Sandwich
Frutas
5| | | | |
10| | | | | | | | | |
6| | | | | |
9| | | | | | | | |
(1/1)
Los palitos de queso.
1. Observar la ilustración y
captar el tema. [A]
M: ¿Cuáles alimentos observan
en la ilustración?
RP: Pizzas, frutas, sandwiches,
palitos de queso.
M: ¿Cómo podemos contar los
alimentos nombrados?
RP: Juntándolos todos y contán-
dolos.
RP: Agrupándolos por tipo de ali-
mentos.
2. Contar el número de ali-
mentos. [A1]
* Enfatizar que por cada ali-
mento nombrado se hace una
marca ( | ).
* Orientar el conteo de las mar-
cas que representan a cada
alimento nombrado.
* Confirmar el número de mar-
cas por cada alimento.
M: ¿Cuántas marcas hay por
cada alimento?
3. Interpretar datos en forma
de tablas. [A2]
M: ¿Cuál es el alimento que más
gusta?
RP: Los palitos de queso.
Continúa en la siguiente página…

156. Guía para maestros/as- Matemática 20
Grado 137
[Continuación]
Recoleccionemos y organicemos
datos en tablas
Lección 1:
(1/1)
… viene de la página anterior
4. Observar el dibujo y captar
el tema. [B]
M: ¿Qué observan en el dibujo?
* Confirmar que hay varios tipos
y cantidades de animales.
* Sería mejor preparar los dibujos
para presentar en la pizarra.
M: ¿Cuál animal hay más?
RP: Tal vez los perros. No sé, hay
que contarlo.
Que sientan la necesidad de
organizar los datos.
5. Contar el número de polli-
tos. [B1]
M: Vamos a contar los pollitos.
M: ¿En qué tuvieron cuidado al
contar?
Que se den cuenta de los puntos
importantesparalarecopilacióny
el conteo de los datos como ser
quenosecuente2veces,queno
se queden cosas sin contar.
* Demostrar la forma de contar
confirmando el número de po-
llitos (véase Columnas).
6. Organizar los datos en la ta-
bla. [B2]
M: Vamos a escribir el número de
cada animal en la tabla.
Continúa en la siguiente página…
1 Cuente cuántos pollitos hay.
2 Escriba en la tabla el número que representa la cantidad de cada animal.
Animal
Número
La tabla sirve para organizar los datos.
[Número de animales]
4 pollitos
B Vamos a investigar el número de los animales.
ciento siete 107
4 5 7 2 6 4

157. Unidad 9 - Estadística138
El objetivo del arreglo estadístico es aclarar la caracterís-
tica de un conjunto o grupo de datos. Representar en la
tabla o en la gráfica no es el objetivo sino el medio. Por
lo tanto, es importante desarrollar la clase con un objetivo de
aclarar la característica de un conjunto a través de usar la tabla.
[Continuación]
Recoleccionemos y organicemos
datos en tablas
Lección 1:
(1/1)
… viene de la página anterior
7. Resolver los ejercicios 1 y 2 .
1 Manuel y Guadalupe hicieron una investigación para saber cuál es la fruta
que más gusta entre sus compañeros y compañeras.
(1) Exprese el resultado en la tabla.
108 ciento ocho
Fruta Número
La fruta que les gusta
2 Los compañeros y compañeras de Leysi hicieron una encuesta para saber cuál
es el deporte que más les gusta.
(1) Exprese el resultado en la tabla.
Deporte Número
El deporte que les gusta
Tenis de mesa
Béisbol
Atletismo
Ciclismo
Baloncesto
2
5
7
3
3
1
4
1
2
2

158. Guía para maestros/as- Matemática 20
Grado 139
Interpretemos pictogramasLección 2:
(1/1)
• Interpretar pictogramas.Objetivo:
1. Observar la ilustración y
captar el tema. [A]
M: ¿Qué observan el patrón que
llevan los helados?
M: Vamos a contar los helados
que comió Luis.
RP: Luis comió 9 helados.
2. Contar el número de helados.
M: Vamos a contar los helados.
3. Resolver el ejercicio 1 .
(M) cartulina, papel, lápices de colores.Materiales:
Lección 2: Interpretemos pictogramas
Vamos a leer una pictografía.
¿Cuántos helados comió Luis?
Escriba el número total de los helados.
¿Quién comió más helados, Irsi o Marcos?
A
1
4
2
3 ¿Quién fue el que comió menos helados de todos?
ciento nueve 109
La pictografía usa dibujos o símbolos para representar datos.
Luis
Marcos
Irsi
Zayuri
1 Resuelva
Respuesta:
Planteamiento de la operación:
(1) ¿Cuál operación usaría para saber
el número de helados comidos por
Irsi y Luis juntos?
(3) ¿Cuántos helados consume Irsi si
come la misma cantidad dos días
seguidos?
(2) ¿Cuántos helados comió Marcos
más que Luis?
(1/1)
12 + 6 + 9 + 3 = 30
6 helados
Marcos
Zayuri
30 Helados
Suma
18 helados
6 helados

159. Unidad 10 - Tiempo140
• Desarrollan el concepto de tiempo.
• Identifican unidades de tiempo (minuto, hora, día, semana, mes, año) en la medición de la duración
de diversos eventos, procesos o actividades.
• Leen la hora en punto y la hora y minuto en reloj de aguja y digital.
Expectativas de logro1
Tiempo (5 horas)Unidad
1010
1/2~2/2 • El mecanismo y el papel del reloj de aguja
3 Plan de estudio (5 horas)
1. Leamos el reloj
(2 horas) • Lectura y representación de la hora en punto y hora
y minutos
1/32. Midamos el tiempo
(3 horas)
• Concepto del tiempo
2/3 • Unidades oficiales de tiempo
(día, semana, mes y año)
3/3 • Determinación de la fecha y el tiempo con el
calendario
• Unidades de tiempo (minuto y hora)
Tiempo
• Concepto de tiempo.
• La hora en punto.
• Diferencia entre la hora
y el tiempo.
• Unidades de tiempo: mi-
nuto, hora, día, semana,
mes y año.
• Manejo del tiempo con
el calendario.
Tiempo
• La hora y media.
• La hora y minutos.
• Unidad de tiempo:
segundo.
• Representación de
tiempo con fracciones.
Tiempo
• Comparación de valores
relativos al tiempo: día,
semana, mes y año.
Relación y desarrollo2

160. Guía para maestros/as - Matemática 20
Grado 141
Materiales
• Cartulina o cartón
• Broche
• Marcadores
• Compás, regla
• Tape (Transparente)
Proceso
1. Hacer un círculo en cartulina o cartón con el compás, cuyo radio sea entre 14 y 15 cm.
2. Escribir los números.
Para que haya una distribución equitativa en la distancia de los números, se escriben primero
los números 12, 6, 3 y 9 en ese orden. Luego se distribuyen los demás números teniendo el
cuidado que la distancia entre dos números consecutivos sea igual. (En el reloj entre 2 núme-
ros consecutivos hay 30 grados y entre 2 divisiones cortas hay 6 grados).
3. Hacer en cartulina o cartón una aguja grande
de (7 cm) y una aguja pequeña de (5 cm)
(si se tiene masking-tape se pueden forrar)
4. Hacer un agujero en el centro del círculo y colocar el broche junto con las agujas.
Puntos de lección
• Lección 1: Leamos el reloj
Para que los niños y las niñas entiendan y
puedan utilizar la lectura de la hora en punto.
Es necesario que usando el reloj comprendan
que la aguja larga indica los minutos y la corta
indica las horas. Al dar la clase es recomen-
dable relacionar la lectura del reloj con las di-
ferentes actividades que los niños y las niñas
realizan en la vida cotidiana para que sientan
la necesidad de leer el reloj y también desa-
rrollen la cultura de la puntualidad y el buen
uso del tiempo a través del estudio.
Para que los niños y las niñas lean correc-
tamente el reloj, el maestro o la maestra de-
berán garantizar el tiempo suficiente para el
desarrollo de las actividades donde manejen
el reloj usando un modelo del mismo y que se
orienten no sólo en esta unidad sino durante
toda la vida escolar.
• Lección 2: Midamos el tiempo
Para los niños y las niñas es difícil distinguir
entre “la hora exacta” y “la duración del tiem-
po”, porque el tiempo no se puede ver, por
lo tanto, se realizan las actividades donde
ellos puedan sentir la duración del tiempo y
también se utiliza la recta para representar la
hora y tiempo para que visualicen y capten el
concepto del tiempo.
4
Elaboración del reloj
Columnas
A
1
B

161. Unidad 10 - Tiempo142
El tiempo y la hora
En la recta numérica la hora se representa con la posición de un punto y el tiempo con la longitud del
segmento. (Véase el siguiente dibujo)
Modelo final
0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12
Con la punta del triángulo se indica
la hora (las 7 de la mañana)
Con la longitud de la cinta se indica el
tiempo transcurrido (7 horas)
Explicación de los dibujos
C
2

162. Guía para maestros/as - Matemática 20
Grado 143
ENERO
FEBRERO
MARZO
JULIO
MAYO
ABRIL
JUNIO
AGOSTO
OCTUBRE
DICIEMBRE
SEPTIEMBRE
NOVIEMBRE
Forma de saber los días que tiene cada mes.
Con los puños de tus manos puedes saber los días que tiene cada mes.
• Los nudillos indican los meses que tienen
31 días.
• Los espacios entre los nudillos indican los
meses que tienen 30 días.
• El mes de febrero sólo tiene 28 ó 29 días.
3

163. Unidad 10 - Tiempo144
Leamos el relojLección 1:
(1/2~2/2)
• Leer correctamente “la hora en punto”.
(M) reloj o modelo de reloj en cartulina o cartón.
(N) reloj o modelo de reloj en cartulina o cartón.
Objetivo:
Materiales:
5 Desarrollo de
clases
1. Captar el tema. [A]
M: ¿En qué orden se realiza cada
actividad?
* En este momento sólo se di-
rigen por la imagen de cada
dibujo para el diálogo entre
maestros y maestras y los ni-
ños y las niñas.
2. Encontrar la manera de leer
la hora en punto en el reloj.
[A1]
M: Observen el dibujo (1). ¿Qué
hora es?
* Indicar que lean las horas re-
presentadas en los relojes (2),
(3) y (4).
Que se den cuenta que cuan-
do se dice la “hora en punto”
la aguja larga señala el 12 y la
aguja corta señala el número
que representa “la hora”. Mos-
trando en el reloj modelo.
3. Escribir la hora en punto con
los números. [A2]
* Orientar la forma oficial de escri-
bir la hora con los números y ex-
plicar que para separar las horas
de los minutos se utiliza (:) dos
puntos, por ejemplo: “6:00”.
* En este momento es más impor-
tante la lectura de la hora en pun-
to en el reloj, que su escritura.
4. Pensar en la función del reloj
y sus partes. [A3]
* Aprovechar la experiencia de la
elaboración del modelo del reloj
para confirmar para que sirve el
reloj, cuáles son sus partes y
sus funciones, pidiendo las opi-
niones a los niños y niñas.
* Confirmar que la aguja horario
es más corta que la aguja mi-
nutero. Aprovechar para enfati-
zar que de un número a otro en
el reloj hay 5 minutos.
5. Resolver los ejercicios 1 y 2 .
(1) Se puede utilizar una hora clase para la elaboración
de los relojes que hay en las hojas para recortar.
(2) Antes de iniciar esta clase es recomendable desarrollar
una conversación donde los niños y las niñas tengan la oportu-
nidad de recordar y expresar todas las actividades que realizan en el
día imaginando el transcurso del tiempo para despertar el interés de
aprender la hora en el reloj.
Lección 1: Leamos el reloj
Unidad 10
A Observe y diga el orden en que se realiza cada actividad.
110 ciento diez
Tiempo
1 Lea la hora que indica el reloj de la actividad (1).
1, 4, 3 y 2.
Son las 6 en punto.
2 Escriba con los números la hora que indica el reloj (1).
Cuando se representa la hora en punto en el reloj, la aguja larga señala
el número 12 y la aguja corta señala el número que representa la "hora".
6:00
(1) (2) (3) (4)
El reloj sirve para saber la hora.
Tiene 2 agujas:
La aguja corta indica las horas.
La aguja larga indica los minutos.
Para separar las horas de los minutos se usa dos puntos (:).
Igual que los
relojes digitales.
2 Escriba en el espacio la hora que marca cada reloj.
3 Piense en la función del reloj y sus partes.
(2) (3) (4)
1 Lea y escriba con los números la hora que indica el reloj (2), (3) y (4).
: : : :
: : :4 00
5 00 9 00 3 0011 00
12 00 7 00
(1/2 ~ 2/2)

164. Guía para maestros/as - Matemática 20
Grado 145
Leamos el relojLección 1:
(1/2~2/2)
[Continuación]
6. Leer la hora y minuto, y es-
cribir en el reloj. [B]
M: ¿Qué hora muestra el reloj?
(Mostrando el reloj modelo)
* Asistir y animar a las parejas
a que realicen la práctica de
señalar la hora en punto en el
reloj modelo.
* Confirmar que la aguja minu-
tero le da una vuelta completa
al reloj en una hora.
7. Resolver los ejercicios 3 y 4 .
* Indicar que en sus casas mi-
dan el tiempo de algunas acti-
vidades que tarden segundos,
minutos, horas como el anun-
cio de la TV, el juego, etc.
111ciento once
B ¿Qué hora marca cada reloj?
1 Practique en pareja la lectura de la hora y minutos usando el reloj modelo.
4 Dibuja el minutero para mostrar la hora y minutos.
3 Lea y escriba la hora de cada reloj.
:3 25
:4 00 :12 00 :11 55
Tres horas y
veinticinco minutos.
La hora que marca el reloj se escribe 3:25 y se lee
«tres horas veinticinco minutos».
:5 40 :9 20
Cinco horas y
cuarenta minutos.
Nueve horas y
veinte minutos.
:3 35 :6 05 :1 50
Tres horas y treinta
y cinco minutos.
Seis horas y
cinco minutos.
Una hora y
cincuenta minutos.

165. Unidad 10 - Tiempo146
Midamos el tiempoLección 2:
(1/3)
• Captar la diferencia entre la hora y el tiempo.
• Reconocer las unidades oficiales del tiempo (minuto
y hora).
(M) reloj o modelo de reloj.
(N) reloj o modelo de reloj.
Objetivo:
Materiales:
1. Captar el tema de la clase.
[A]
* Indicar que comenten los di-
bujos.
2. Decir la hora que marca cada
dibujo. [A1]
M: ¿A qué hora salió Ana de su
casa (pasó por la iglesia, lle-
gó a la escuela)?
3. Encontrar el tiempo. [A2]
(Véase columnas)
M: ¿Cuánto tiempo tardó Ana de
su casa a la iglesia?
RP: 20 minutos.
M: ¿Cómo lo encontraron?
M: ¿Cuánto tiempo tardó de la igle-
sia a la escuela?
* Orientar que en este caso hay
que encontrar los minutos desde
las 6 y 20 hasta las 7 en punto.
M: ¿Con qué unidad se puede me-
dir la duración del tiempo?
* Concluir que una de las uni-
dades de medida de tiempo
se llama “minuto”.
* Indicar que cierren los ojos du-
rante un minuto para que per-
ciban la duración del tiempo.
Que capten que la hora en
punto es un punto y el tiempo
es la longitud.
M: ¿Cuántos minutos tardó Ana
de su casa a la escuela?
RP: 60 minutos.
* Si hay niños y niñas que dicen
que es una hora, aprovechar
su opinión para concluir que 1
hora equivale a 60 minutos.
Que se den cuenta que al dar
una vuelta la aguja larga cuenta
60 minutos y es igual a 1 hora.
4. Resolver el ejercicio 1 .
* Indicarquehaganalgunoscuen-
tos viendo los dibujos (Véase
Notas) o imaginando las activi-
dades de ellos mismos.
[Ejemplo del cuento]
- La hora que Ana entra al recreo es a las 10 en punto.
Lección 2: Midamos el tiempo
A Observe.
1 Diga la hora en que Ana hizo cada actividad.
(1) 6 en punto.
(2)
(3)
2 Encuentre el tiempo.
20 minutos.
(2)
40 minutos.
El minuto es una unidad oficial de medida del tiempo.
(3)
60 minutos ó 1 hora.
(1)
¿A qué hora salió Ana de su casa?
¿A qué hora pasó Ana por la iglesia?
¿A qué hora llegó Ana a la escuela?
¿Cuánto tiempo tardó Ana de la iglesia a la escuela?
¿Cuánto tiempo tardó Ana de su casa a la escuela?
¿Cuánto tiempo tardó Ana de su casa a la iglesia?
60 minutos equivalen a 1 hora.
1 hora = 60 minutos
112 ciento doce
Cuando la aguja larga da
una vuelta completa es
una hora.
6 y 20 minutos.
7 en punto.
1 Haga cuentos con la hora y el tiempo, viendo los dibujos.
12 1
2
3
4
567
8
10
11
9
(1/3)
Se omite la solución

166. Guía para maestros/as - Matemática 20
Grado 147
Midamos el tiempoLección 2:
(2/3)
• Reconocer las unidades oficiales de tiempo (día, se-
mana, mes y año).
(M) calendario, reloj.
(N) calendario, reloj.
Objetivo:
Materiales:
1. Captar el tema de la clase.
[B]
* Indicar que comenten las imá-
genes del LE.
Que capten que hay unidades
de tiempo más grandes que
las horas.
2. Encontrar el tiempo equiva-
lente a un día. [B1]
M: ¿Cuánto tiempo ha pasado des-
de las 11 de la mañana de ayer
hasta las 11 de la mañana de
hoy?
RP: 1 día.
* Concluir que el día es una uni-
dad oficial de tiempo.
3. Confirmar las horas que tie-
ne un día con el reloj. [B2]
* Indicar que utilicen el reloj para
investigar la cantidad de horas
que tiene un día proponiéndo-
les una hora como referencia.
M: ¿Cuántas horas hay en un día?
RP: Hay 24 horas.
M: ¿Cómo resolvieron?
RP: Movimos las agujas del reloj
contando las horas una por una.
Nosotros pasamos dos veces
por el mismo número, diciendo
día y noche.
Que se den cuenta que se pasa
dos veces por el mismo número
porqué el día tiene la mitad luz y
la mitad noche.
4. Identificar la distribución de
las horas de un día. [B3]
* Indicar que observen la ima-
gen del LE.
M: ¿Cuántas horas están antes
del mediodía y cuántas horas
están después del mediodía?
* Explicar que se escribe “a.m.”
para las horas que estan antes
del mediodía y “p.m.” para las
horas después del mediodía.
Es probable que los niños y las niñas opinen que las horas
antes del mediodía se dividen en: madrugada y mañana y
que las horas después del mediodía se dividen en: tarde y no-
che, en este caso demostrar la división con la recta numérica, así:
B Observe y comente.
1 ¿Cuánto tiempo pasó entre A y B?
1 día
La unidad de tiempo más grande que las horas se llama día.
El día es una unidad oficial de tiempo.
2 Confirme cuantas horas tiene 1 día usando el reloj.
3 Identifique la distribución de horas de un día.
El día
tiene
24 horas
12 horas antes
del mediodía
mediodía
12 horas
pasado el
mediodía
a.m.
m.
p.m.
A B
Sábado Domingo
El día tiene mitad
luz y mitad noche.
24 horas
1 día = 24 horas
ciento trece 113
(2/3)

167. Unidad 10 - Tiempo148
Lección 2:
(2/3)
Midamos el tiempo5. Identificar otras unidades
oficiales de tiempo. [C]
M: ¿Qué otras unidades oficiales
de tiempo hay?
RP: Semana, mes y año.
6. Conocer la relación de cada
unidad.
* Indicar que observen el ca-
lendario que está en el LE y
aprovechar para establecer
la relación que hay entre las
medidas de tiempo (día, se-
mana, mes y año).
M: ¿Cuántos días tiene una se-
mana? ¿Cuántos días tiene
un mes?
M: ¿Cuántas semanas tiene un
mes?
Que se den cuenta que algu-
nos meses tienen 4 semanas y
otros tienen 5 semanas
7. Encontrar el tiempo entre
dos fechas dadas usando el
calendario. [D]
M: ¿Cómo se puede encontrar
cuántos días hay desde el
cumpleaños de Rafael al cum-
pleaños de Víctor?
RP: Contando los días. Usando el
calendario. Restando, etc.
M: Cuenten, ¿cuántos días hay?
RP: 22 días. 23 días. 21 días.
M: ¿Por qué dio diferentes resul-
tados?
* Pedir a algunos voluntarios o
voluntarias que expresen sus
ideas.
* Es mejor confirmar bien los días
que se van a contar, es decir,
desde dónde se empieza y has-
ta dónde termina.
* Aprovechando la hoja del calen-
dario dar otras fechas para que
puedan encontrar el tiempo, se
puede usar la fecha de cum-
pleaños de los niños y niñas.
8. Resolver el ejercicio 6 .
[Continuación]
ciento catorce
1 semana = 7 días
1 mes = 30 días (31 días)
1 año = 12 meses (365 días)
Día, semana, mes y año son unidades oficiales de tiempo.
C ¿Qué otras unidades de tiempo hay y cuál es su relación?
2006
Cuando el mes de
febrero tiene 29 días
se llama año bisiesto
porque tiene 366 días
y sucede cada 4 años.
Semana, mes y año.
114
D ¿Cuántos días hay desde el cumpleaños de Rafael al cumpleaños de Víctor?
22 días
Cumplió años
el 25 de febrero.
Cumplió años
el 3 de febrero.
6 Resuelva usando el calendario.
¿Cuántos días hay desde el 8 de febrero hasta el 23 de febrero?(1)
(2) ¿Cuántos días hay desde el 5 de febrero hasta el 26 de febrero?
(3) ¿Cuántos días hay desde el 11 de marzo hasta el 28 de marzo?
15 días
21 días
17 días

168. Guía para maestros/as - Matemática 20
Grado 149
Midamos el tiempoLección 2:
(3/3)
• Encontrar la fecha y el tiempo usando el calendario.
(M) calendario.
(N) calendario.
Objetivo:
Materiales:
1. Encontrar la fecha a partir de
una fecha inicial dada. [E]
Que capten que hay que en-
contrar la fecha que es 7 días
después del día 14 de julio.
M: ¿Cómo encontraron la res-
puesta?
RP: Usé el calendario y conté 7
días después del 14. A 14 le
sumé 7.
* La importancia es saber desde
donde se empieza a contar.
2. Resolver el ejercicio 7 .
3. Captar fechas en meses
usando el calendario. [F]
M: ¿Cuántos meses después es
el cumpleaños de Claudia?
M: ¿Cómo podemos averiguarlo?
RP: Contando
* Confirmar que como hay me-
ses de 30 y de 31 días es
conveniente inducir al conteo
usando el calendario.
4. Resolver el ejercicio 8 .
La dificultad en encontrar el tiempo es saber si se cuenta el
día de la primera fecha o partir del siguiente día; si se toma
en cuenta el día de la última fecha o no, para evitar la equi-
vocación primero se tiene que definir la manera de contar los
días en el calendario. Es recomendable usar las fechas que se pueden
encontrar sumando. Cuando se usa fechas que pasan de un mes a otro es
mejor usar el calendario porque hay meses que tienen 30 días y otros 31
días; y también considerar el mes de febrero como caso especial.
Julio
E Si Roberto cumple años el 14 de julio y Pedro cumple 7 días después,
¿en qué fecha cumple años Pedro?
21 de julio
7 Resuelva usando el calendario.
(1) ¿Qué fecha es 25 días después del 3 de mayo?
(2) ¿Qué fecha es 2 semanas después del 16 de junio?
(3) ¿Qué fecha es 3 meses después del 30 de agosto?
Yo encontre
la fecha sumando
14 + 7 = 21
Julio
??
Roberto Pedro
ciento quince 115
MayoMarzo 20062006
F ¿Cuántos meses hay desde el cumpleaños de José al cumpleaños de Claudia?
2 meses
(1) ¿Cuántos meses hay desde el 1 de enero hasta el 31 de enero?
(2) ¿Cuántos meses hay desde el 30 de junio hasta el 30 de septiembre?
8 Resuelva usando el calendario.
ClaudiaJosé
28 de mayo
30 de junio
30 de noviembre
(3/3)
1 mes
3 meses

169. Unidad 11 - Moneda Nacional150
• Identifican monedas y billetes de circulación nacional.
• Establecen equivalencias del peso dominicano con monedas y billetes de circulación en nacional.
• Utilizan monedas y billetes en situaciones de la vida diaria.
Expectativas de logro1
Moneda Nacional (3 horas)Unidad
1111
1/1 • Identificación de los billetes de 100, 200 y 500
pesos
3 Plan de estudio (3 horas)
1. Identifiquemos monedas y
billetes de la República Domi-
nicana
(1 hora)
1/12. Cambiemos dinero
(1 hora)
• Equivalencia entre monedas y billetes hasta 500
pesos
1/13. Aprendamos a usar el dinero
(1 hora)
• Resolución de problemas de la vida diaria usando
el dinero de circulación nacional
Moneda nacional
• Identificación de billetes
de 100, 200 y 500 pe-
sos.
• Equivalencia entre mo-
nedas y billetes menor
que 1,000.
• Utilización de monedas
y billetes menores que
1,000.
Moneda nacional
• Identificación de billetes
de 1,000 y 2,000 pesos.
• Equivalencia entre mo-
nedas y billetes.
• Utilización de monedas
y billetes.
Moneda nacional
• Identificación de mone-
das de uno, cinco, diez
y veinticinco pesos.
• Identificación de billetes
de diez, veinte y cin-
cuenta pesos.
• Equivalencia entre mo-
nedas y billetes menor
que 100.
• Utilización de monedas
y billetes menores que
100.
Relación y desarrollo2

170. Guía para maestros/as- Matemática 20
Grado 151
Puntos de lección
• Lección 1: Identifiquemos monedas y bi-
lletes de la República Dominicana
En esta lección pretendemos, recordar lo apren-
dido sobre las monedas y los billetes en el curso
anterior. O sea la identificación y uso de monedas
y billetes menores que 100. Recordarla, compa-
rarla y utilizarla, facilita el proceso de aprendizaje
de esta nueva unidad.
• Lección 2: Cambiemos dinero
A diario las personas tenemos que hacer cam-
bios de dinero para resolver situaciones que
se nos presentan. Regularmente buscamos
equivalencia entre una moneda o billete de
alto valor con otros que al juntarlos represen-
tan un mismo total. En esta lección los niños
y las niñas deberán cambiar billetes de 100,
200 y 500 por otras monedas y billetes cuyos
totales resulten equivalentes. Por ejemplo, un
4
billete de 100 pesos es equivalente a: dos de
50 pesos o por 4 monedas de 25 o por 10
billetes o monedas de 10 pesos, etc. Como
se observa, existen varias maneras de hacer
equivalencias entre las monedas y billetes de
nuestro país. Se trata de que el niño/a pueda
hacer las conversiones para responder a si-
tuaciones que se les presente en la vida.
• Lección 3: Aprendamos a usar el dinero
Aunque los niños y las niñas han hecho cambios
o equivalencias con el dinero, esto no necesaria-
mente implica usar dicho dinero en situaciones
de la vida. En esta lección tratamos de presentar
situaciones del entorno para el uso práctico de la
vida. Hacer simulaciones de ventas y compras
ligadas a la vivencia del niño y la niña contribuirá
a valorar este aprendizaje por su aplicación en
la vida.

171. Unidad 11 - Moneda Nacional152
Identifiquemos monedas y billetes
de República Dominicana
Lección 1:
(1/1)
• Identificar los billetes mayores o iguales a 100 que
circulan en la República Dominicana. (100, 200 y 500
pesos)
(M) y (N) Monedas de 1, 5, 10 y 25 pesos. Billetes de
10, 20, 50, 100, 200 y 500 pesos en carteles, copias,
láminas, etc., extraídos de las páginas de recortar.
Objetivo:
Materiales:
5 Desarrollo de
clases
1. Captar el tema y despertar
el interés de los niños y las
niñas. [A1]
* Invitar a los niños y las niñas
a observar el dibujo y luego
contestar:
M: ¿Con qué billete está pagan-
do el niño?
2. Identificar características de
los billetes mayores o igua-
les a 100 de circulación en la
República Dominicana. [A2]
M: ¿Cuáles imágenes aparecen
en los billetes de 100, 200 y
de 500?
* Invitar a socializar lo que en-
contraron.
Que conecten estas imágenes
con figuras nacionales y re-
fuercen su identidad nacional.
Continúa en la siguiente página…
Lección 1:
Unidad 11 Moneda Nacional
A1
116 ciento dieciséis
Identifiquemos monedas y billetes de la
República Dominicana
2 Observe los billetes que circulan en el
país y comente sobre sus características.
Observe y comente con qué billete
pagó el niño.
HELADERIA
Helado Helado Helado
Recordemos
1. Escriba en la línea el valor en pesos de cada moneda y billete.
_____
__________ _____
__________ _____
(1/1)
50
105 1
2020 10

172. Guía para maestros/as- Matemática 20
Grado 153
117
3 Dibuje un círculo encima de los billetes de 100, un cuadrado encima de los
billetes de 200 y un triángulo encima de billetes de 500.
ciento diecisiete
1 Escriba el valor en pesos de cada billete en la línea.
(1)
(6)
_____ __________
_____
(2) (3)
(7) (8) (9)
(4)
_____ _____
_____ _____
(5)
(10) (11) (12)
_____ _____
_____
_____
20 50 500
10 500 100
100
50 10
20200
200
[Continuación]
Lección 1:
(1/1)
… viene de la página anterior
3. Conocer las monedas y bi-
lletes de la República Domi-
nicana. [A3]
* Invitar a los niños y a las niñas a
dibujar un círculo encima de los
billetes de 100, un cuadrado en-
cima de los billetes de 200 y un
triángulo encima de los billetes
de 500.
4. Resolver el ejercicio 1 .
Identifiquemos monedas y billetes
de República Dominicana

173. Unidad 11 - Moneda Nacional154
1. Despertar el interés de los
niños/as.
* Organizar un juego donde los
niños/as tengan que cambiar
monedas y billetes ya cono-
cidas. Presentar un nuevo
desafío. “La competencia”.
(Véase notas)
2. Cambiar billetes de 100,
200 y 500 pesos por otros
de menor valor pero que al
juntarlo se obtiene el mis-
mo valor. [A1], [A2] y [A3].
M: ¿Alguno cambió el billete de
100, 200 y 500?
* Motivar para que presenten las
soluciones de cambio del bille-
te de 100, 200 y 500.
M: ¿Cómo lo hizo?
* Invitar a los niños y a las ni-
ñas a presentar varias formas
de cambiar los billetes.
* Si no salen todas las posibles
combinaciones, motivar para
que busquen otras formas.
De no llegar el niño o la niña,
debe inducirla.
Que los niños y las niñas com-
prendan que un mismo billete
de 100, 200 y 500 es equiva-
lente a varios billetes y/o mo-
nedas de menor valor.
3. Resolver los ejercicios 1 .
Lección 2:
(1/1)
Cambiemos dinero
___________________
___________________
___________________
___________________
ciento dieciocho
Cambie 100 pesos de diferentes maneras.
50 25 25,
Lección 2: Cambiemos dinero
118
1 Una con una línea, las monedas y billetes que utiliza para representar las cantidades.
(1) 125 pesos (2) 700 pesos (3) 110 pesos (4) 650 pesos (5) 200 pesos
seis billetes
de 100 y dos
monedas de 25
dos billetes
de 100 pesos
un billete de
500 pesos y un
billete de 200
un billete
de 100 y una
moneda de 25
un billete de 50,
dos monedas de 25
y un billete de 10
___________________
___________________
___________________
___________________
3 Cambie 500 pesos de diferentes maneras.
___________________
___________________
___________________
___________________
2 Cambie 200 pesos de diferentes maneras.
100 50 50
200 200 100
A1
(1/1)
Se omite la respuesta
Se omite la respuesta
Se omite la respuesta
• Realizar equivalencias entre billetes y monedas de
circulación nacional.
(M) y (N) Monedas de 1, 5, 10 y 25 pesos. Billetes de
10, 20, 50, 100, 200 y 500 pesos en carteles, copias,
láminas, etc., extraídos de las páginas de recortar.
Objetivo:
Materiales:
La competencia es un juego en el cual se forman dos
grupos. Ambos tienen unos representantes y otros par-
ticipantes con billetes enteros que hay que cambiar. So-
bre dos mesas con vigilantes existen monedas y billetes para
el cambio. Se trata de que el representante del grupo trate de hacer
cambios en los billetes del grupo contrario. Gana el que logre hacer los
cambios más rápido. Incluir billetes de 100.

174. Guía para maestros/as- Matemática 20
Grado 155
Aprendamos a usar el dineroLección 3:
(1/1)
• Resolver problemas de la vida diaria usando el dinero
de circulación nacional.
(M) y (N) Monedas de 1, 5, 10 y 25 pesos. Billetes
de 10, 20, 50, 100 y 500 pesos en carteles, copias,
láminas, etc., extraídos de las páginas de recortar.
Objetivo:
Materiales:
1. Comentar la situación del
problema. [A]
* Orientar para que piensen
con cuál operación se puede
encontrar el resultado.
2. Encontrar la respuesta. [A1]
M: ¿Cómo será el PO y su resul-
tado?
3. Calcular las posibles com-
binaciones. [A2]
M: ¿Cómo devolvió el chofer a su
pasajero?
* Invitar a presentar varias formas
de cómo pudo devolver el cho-
fer a su pasajero.
* Si no salen todas las posibles
combinaciones, motivar para
que busquen otras formas.
De no llegar el niño o la niña,
debe inducirla.
4. Identificar cuántos artículos
se pueden comprar con un
billete de 500 pesos. [A3]
M: ¿Cuáles artículos se pueden
comprar con un billete de 500
pesos?
* El niño o la niña puede esco-
ger varias combinaciones de
artículos.
ciento diecinueve
Lección 3: Aprendamos a usar el dinero
119
El pasaje cuesta 12 pesos y
un pasajero pagó con 25 pesos.
3 Observe los siguientes artículos y encierre en un círculo cuántos de
ellos puede comprar con un billete de 500 pesos.
175 95 200 250
15 8 45
1 ¿Cuántos pesos debe devolver el chofer?
2 ¿Cómo puede devolver el chofer?
(Ejemplo)
(1) (2)
(3) (4)
PIZZA
Galletas rellenas
Jugo de
Naranja
Hech
o en
Repú
blica
Dominican
a
A
Planteamiento de la operación: 25 - 12 = 13
Respuesta: 13 pesos
80
un billete de
10 pesos
tres monedas
de 1 peso
+
(1/1)
Se omite la respuesta
una moneda
de 10 pesos
tres monedas
de 1 peso
dos monedas
de 5 pesos
tres monedas
de 1 peso
una moneda
de 5 pesos
ocho monedas
de 1 peso
trece monedas
de 1 peso

176. Guía para maestros/as - Matemática 20
Grado 157

177. 158 Guía para maestros/as - Matemática 20
Grado

178. Guía para maestros/as - Matemática 20
Grado 159

179. 160 Guía para maestros/as - Matemática 20
Grado

180. Guía para maestros/as - Matemática 20
Grado 161

181. 162 Guía para maestros/as - Matemática 20
Grado

182. Guía para maestros/as - Matemática 20
Grado 163

183. 164 Guía para maestros/as - Matemática 20
Grado
1
Por haber aprobado la memorización de:
Las tablas de la multiplicación
33
678
9
2
5
4

184. Guía para maestros/as - Matemática 20
Grado 165

185. 166 Guía para maestros/as - Matemática 20
Grado

186. Guía para maestros/as - Matemática 20
Grado 167

187. 168 Guía para maestros/as - Matemática 20
Grado
Moneda nacional

188. Guía para maestros/as - Matemática 20
Grado 169

189. 170 Guía para maestros/as - Matemática 20
Grado
1 tarjeta de figura triangular
Formaron los cohetes con 9 tarjetas de la figura triangular cada uno.
Pero hay un cohete que no se puede formar con 9 tarjetas.
¿Cuál es?
Vamos a dividir la
figura de cohete en
las tarjetas triangulares
trazando líneas.
Nos divertimos
1
2
3
¡ Forme cohetes !

190. Guía para maestros/as - Matemática 20
Grado 171

191. 172 Guía para maestros/as - Matemática 20
Grado

192. Guía para maestros/as - Matemática 20
Grado 173

193. 174 Guía para maestros/as - Matemática 20
Grado

194. Guía para maestros/as - Matemática 20
Grado 175
260 cm
140 cm3 m 5 cm
1 dm 4 cm
2 m 815 cm
5 dm
350 cm 200 cm
500 cm
2 dm 6 cm
2 m 6 cm
305 cm
14 m
8 m 15 cm
5 m
C
Una con la línea los puntos que representa la misma longitud.
Aparecerán dis letras para completar un mensaje secreto.
¿Qué dice en el mensaje?
1 m 40 cm
O E E
¿?
¡Qué aparecen!

195. AGRADECIMIENTO
El Instituto Nacional de Formación y Capacitación del Magisterio (INAFOCAM),
como entidad responsable de dirigir y coordinar el proyecto “Mejoramiento de la
Calidad de Enseñanza de la Matemática” 2005-2010, JICA-MINERD, quiere expre-
sar su más sincero agradecimiento al gobierno del Japón, y de una manera muy par-
ticular, a la Agencia de Cooperación Internacional del Japón (JICA) y a la dirección
del Proyecto Regional “Me Gusta Matemática”, por el apoyo para la elaboración
e impresión del valioso material (Guía para maestros/as), como herramienta para
orientar la mejora en el aprendizaje de la matemática de los niños/as del Primer
Ciclo de Básica.
Del mismo modo, agradecemos a nuestras autoridades y funcionarios del Sistema
Educativo Nacional que pusieron su confianza y apoyo al plan de mejora desarrolla-
do. A las Regionales 03 de Azua, 05 de San Pedro de Macorís, 08 de Santiago y 15 de
Santo Domingo, así como a los Distritos 03-01, 05-02, 08-05 y 15-03 que facilitaron
en su gestión la implementación, además de disponer de recursos humanos para el
logro de los objetivos del mismo.
De manera especial queremos agradecer al Grupo Núcleo, al Grupo Operativo de
los distritos y regionales implicados, a los asesores nacionales e internacionales, a
los voluntarios japoneses, a los directores y docentes de los veinte y un centros edu-
cativos involucrados, así como al equipo administrativo (secretarias, diagramado-
res, personal de apoyo, colaboradores) que hicieron posible la edición y validación
de esta herramienta didáctica. Gracias a todos/as.

196. Guía para Maestros y Maestras
MatemáticaGuíaparaMaestrosyMaestras
Matemática
Agencia de Cooperación
Internacional del Japón
Instituto Nacional de
Formación
y
Capacitación del
Magisterio PROYECTO REGIONAL
Me gusta¡
!Matemática JAPÓNAsistencia oficial para el Desarrollo
Grado2do
Grado
2do