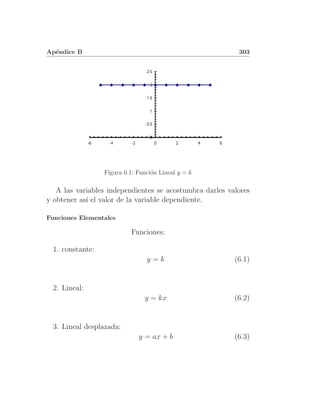
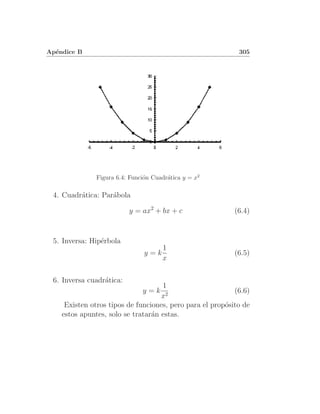
Este documento presenta apuntes de física I. Contiene tres unidades principales: introducción al conocimiento de la física, movimiento y leyes de Newton, trabajo, potencia y energía. En la primera unidad se definen conceptos básicos de física como magnitudes y sistemas de unidades. La segunda unidad cubre temas de movimiento como movimiento rectilíneo uniforme, movimiento rectilíneo uniformemente acelerado y movimiento circular. La tercera unidad explica las leyes de Newton, trabajo, potencia, energía mecánica y colision

1. APUNTES DE F´
ISICA I
———————–
Reg. No.: 03-2007-02413370900-01
Queda prohibida su reproducci´n total o parcial
o
por cualquier medio, fisico o electr´nico,
o c. Dr. Neptal´ Z´rate V´squez
ın a a
sin el el permiso de autor. Profesor de F´
ısica
Tlaxcala, Tlax., Verano 2007

2. i
Dedicatorias
Al Dios feliz y del orden; El Excelent´ısimo, El poderoso
Se˜ or de los Ej´rcitos. Le damos gracias por permitir-
n e
nos entender un poquito de la grandeza de su creaci´n o
[Jer 31:35, 33:25, Isa. 40:26, Sal. 19:7-11, 2 Tim. 3:16,
Job 26:7, 8, 10-12, 38:-41:, Ecles. 1:4-7, Am´s 5:8].
o

3. ii

4. ´
Indice general
Pr´logo
o 1
UNIDAD I Introducci´n al Conocimiento de la
o
F´ısica 6
1.1. Generalidades . . . . . . . . . . . . . . . . . . . . 8
1.1.1. La F´ ısica y su Impacto en la Ciencia y la
Tecnolog´ ıa. . . . . . . . . . . . . . . . . . 41
1.1.2. Los M´todos de Investigaci´n y su Rele-
e o
vancia en el Desarrollo de la F´ ısica. . . . . 41
1.2. Magnitudes F´ ısicas y su Medici´n. . . . . . . . . .
o 45
1.2.1. Magnitudes Fundamentales y Derivadas. . 48
1.2.2. Sistemas de Unidades CGS e Ingl´s. . . . .
e 50
1.2.3. El Sistema Internacional de Unidades, Ven-
tajas y Limitaciones. . . . . . . . . . . . . 51
1.2.4. M´todos Directos e Indirectos de Medici´n.
e o 56
1.2.5. Notaci´n en Base 10 (Prefijos). . . . . . .
o 56
1.2.6. Transformaci´n de Unidades Entre Siste-
o
mas. . . . . . . . . . . . . . . . . . . . . . 59
1.2.7. 1a Autoevaluaci´n . . . . . . . . . . . . .
o 66
1.2.8. La Precisi´n de los Instrumentos de Me-
o
dici´n, Tipos de Errores. . . . . . . . . . .
o 81
1.3. Vectores. . . . . . . . . . . . . . . . . . . . . . . . 91

5. iv ´
INDICE GENERAL
1.3.1. Diferencia Entre las Magnitudes Escalares
y Vectoriales. . . . . . . . . . . . . . . . . 91
1.3.2. Caracter´ ısticas de un Vector. . . . . . . . . 93
1.3.3. Representaci´n Gr´fica de Sistemas de Vec-
o a
tores. . . . . . . . . . . . . . . . . . . . . . 95
1.3.4. Descomposici´n y Composici´n de Vecto-
o o
res M´todos Gr´ficos y Anal´
e a ıticos. . . . . . 99
UNIDAD II MOVIMIENTO 121
2.1. Movimiento en una Dimensi´n . . . . . . . . . . . 122
o
2.1.1. Conceptos Fundamentales. . . . . . . . . . 122
2.1.2. Sistemas de Referencia (SR). . . . . . . . . 122
2.1.3. Movimiento Rectilineo Uniforme (MRU). . 129
2.1.4. 2a Autoevaluaci´n . . . . . . . . . . . . . 144
o
2.1.5. Movimiento Rectilineo Uniformemente Ace-
lerado (MRUV o MUA). . . . . . . . . . . 150
2.1.6. Caida Libre y Tiro Vertical . . . . . . . . 159
2.2. Movimiento en Dos Dimensiones. . . . . . . . . . 168
2.2.1. Tiro Parab´lico Horizontal y Oblicuo. . . . 168
o
2.2.2. Movimiento Circular. . . . . . . . . . . . . 182
UNIDAD III LEYES DE NEWTON, TRABAJO,
POTENCIA Y ENERG´ IA 200
3.1. Leyes de Newton. . . . . . . . . . . . . . . . . . . 205
3.1.1. Concepto de Fuerza • Tipos • Peso de los
Cuerpos . . . . . . . . . . . . . . . . . . . 205
3.1.2. Fuerzas de Fricci´n Est´tica y Din´mica. . 212
o a a
3.1.3. Primera Ley de Newton (• Ley de Inercia). 215
3.1.4. Segunda ley de Newton (• Ley de Fuerza). 218
3.1.5. 3a Autoevaluaci´n . . . . . . . . . . . . . 231
o

6. ´
INDICE GENERAL v
3.1.6. Tercera Ley de Newton (• Ley de Acci´n o
y Reacci´n). . . . . . . . . . . . . . . . .
o . 238
3.1.7. Ley de la Gravitaci´n Universal. . . . . .
o . 240
3.2. Trabajo, Potencia y Energ´ Mec´nica. . . . . .
ıa a . 248
3.2.1. Trabajo. . . . . . . . . . . . . . . . . . . . 249
3.2.2. Potencia. . . . . . . . . . . . . . . . . . . 250
3.2.3. Energ´ Mec´nica (Potencial y Cin´tica).
ıa a e . 254
3.2.4. Principio de Conservaci´n de la Energ´
o ıa
Mec´nica. . . . . . . . . . . . . . . . . .
a . 257
3.2.5. Impulso y Cantidad de Movimiento. . . . . 260
3.2.6. Principio de la Consevaci´n de la Canti-
o
dad de Movimiento. . . . . . . . . . . . . . 264
3.2.7. Colisiones (Choques) . . . . . . . . . . . . 266
3.2.8. Coeficiente de Restituci´n . . . . . . . .
o . 273
a
3.2.9. 4 Autoevaluaci´n . . . . . . . . . . . .
o . 283
Bibliograf´
ıa 295
Ap´ndices
e 300
6.1. Apendice A: Respuestas a Preguntas y Ejercicios 302
6.2. Apendice B: Funciones y Gr´ficas . . . . . . . . . 302
a
6.3. Apendice C: Tipos de Proporcionalidad . . . . . . 307

7. vi ´
INDICE GENERAL

8. ´
Indice de cuadros
1.5. Unidades Fundamentales en tres Sistemas de Uni-
dades. . . . . . . . . . . . . . . . . . . . . . . . . 52
1.6. Unidades Fundamentales del SI. . . . . . . . . . . 54
1.7. Equivalencia entre Sistemas de Unidades. . . . . . 55
1.8. Potencias de Base 10 . . . . . . . . . . . . . . . . 58
2.1. Tabla de datos del ejemplo: 2.1.3.1 . . . . . . . . 133
2.2. para el problema 3 . . . . . . . . . . . . . . . . . 149
2.3. Ecuaciones del MRUV. . . . . . . . . . . . . . . . 153
2.4. Ecuaciones del MCUV ´ MCUA . . . . . . . . .
o . 196
3.1. Coeficientes de Rozamiento Cin´tico para Dife-
e
rentes Materiales. . . . . . . . . . . . . . . . . . . 226
3.2. Coeficientes de Rozamiento Est´tico y Din´mico
a a
para Diferentes Materiales. . . . . . . . . . . . . . 230
3.3. Costo por kW − Hr en Tlaxcala abril 2,007 . . . 252

9. viii ´
INDICE DE CUADROS

10. ´
Indice de figuras
1.1. Sabios de la Antig¨edad. . . . . . . . . . . . . . .
u 18
1.2. Cient´ıficos de la Mec´nica Cu´ntica. . . . . . . .
a a 19
1.3. Cient´ıficos de loa Quarks. . . . . . . . . . . . . . 20
1.4. Propiedades de la Materia. . . . . . . . . . . . . . 31
1.5. Representaci´n de un Cubo de Hierro para el Ejem-
o
plo 1.1. . . . . . . . . . . . . . . . . . . . . . . . . 35
1.6. Mapa Conceptual de Fen´meno . . . . . . . . . .
o 38
1.7. Tipos de Fuerza en la Naturaleza. . . . . . . . . . 40
1.8. Componentes de la Materia . . . . . . . . . . . . 40
1.9. Diagrama de flujo del M´todo Cient´
e ıfico. . . . . . 42
1.10. Mapa Conceptual de Los Diferentes Tipos de Erro-
res. . . . . . . . . . . . . . . . . . . . . . . . . . . 85
1.11. Vector y sus Caracter´ ısticas: O: Origen, F: Senti-
do, θx : Direcci´n, X: Eje de Referencia. . . . . . .
o 94
1.12. Clasificaci´n de Vectores 1 . . . . . . . . . . . . .
o 95
1.13. Clasificaci´n de Vectores 2 . . . . . . . . . . . . .
o 96
1.14. Proceso que sufre un vector al actuar en un cuer-
po por el principio de transmisibilidad. . . . . . . 97
1.15. v 20 uv 30◦ ր. Ejemplo: 1.3.3.1 . . . . . . . . . . 98
1.16. 600 km →, figura para el ejemplo: 1.3.3.2. . . . . .
hr 99
1.17. Igualdad de Vectores. . . . . . . . . . . . . . . . . 100
1.18. Vector Negativo de A. . . . . . . . . . . . . . . . 100

11. x ´
INDICE DE FIGURAS
1.19. Suma de Vectores, indicando el N´mero del paso
u
Realizado. . . . . . . . . . . . . . . . . . . . . . . 103
1.20. Soluci´n del Ejemplo 1.3.4.1 V1 = 4 pasos V2 = 3
o
pasos, R = V1 + V2 = 7 pasos →. . . . . . . . . . 104
1.21. Soluci´n al Ejemplo 1.3.4.2 V1 = 10pasos ր,
o
V2 = 7pasos ց, R = V1 + V2 = 12,3 pasos 10◦ ր . 104
1.22. Resta de Vectores, Indicando el N´mero del paso
u
Realizado. . . . . . . . . . . . . . . . . . . . . . . 106
1.23. Suma de Vectores por el M´todo del Pol´
e ıgono . . 107
1.24. Resultante de la suma de los vectores de la figura:
1.23 por el M´todo del Pol´
e ıgono . . . . . . . . . . 108
1.25. Representaci´n de un Vector y sus Componentes
o
Rectangulares . . . . . . . . . . . . . . . . . . . . 109
` ν o` ´ν
1.26. Hipotenusa del gr. υ ιπoτ ǫηo`ςα ´ υ πoτ ǫλ`ω fijar,
sujetar fuertemente una cosa a otra . . . . . . . . 110
1.27. Figura para el Ejemplo 1.3.4.2. . . . . . . . . . . 112
2.1. Observaci´n de un Movimiento y su Vector de
o
Posici´n (r) . . . . . . . . . . . . . . . . . . . . . 124
o
2.2. Sistema de Referencia en Tres Dimensiones . . . . 125
2.3. Vectores de Posici´n (ri ) y Desplazamiento (D =
o
∆r = r2 − r1 ) . . . . . . . . . . . . . . . . . . . . 127
2.4. Figura para el problema: 2.1.2 . . . . . . . . . . . 128
2.5. Posici´n (r), Distancia (x) y Desplazamiento (d =
o
∆r = ∆x) en un Movimiento Rectilineo . . . . . . 129
2.6. Gr´fica del Movimiento Rectil´
a ıneo Uniforme (MRU).132
2.7. Gr´fica d vs t para el ejemplo: 2.1.3.1. . . . . . . 133
a
2.8. Gr´fica d vs t para el MRU . . . . . . . . . . . . 136
a
2.9. Gr´fica r vs t de la figura 2.8. . . . . . . . . . . . 137
a
2.10. Representaci´n gr´fica para el problema 2.1.3.1 . 138
o a
2.11. Representaci´n gr´fica para el problema 2.1.3.2. . 139
o a

12. ´
INDICE DE FIGURAS xi
2.12. Representaci´n gr´fica del problema 2.1.3.3. . . . 140
o a
2.13. Pr´ctica: Movimiento rectil´
a ıneo Uniforme. . . . . 142
2.14. Ejemplo 2.1.5.1 del MRUV . . . . . . . . . . . . . 154
2.15. Ejemplo 2.1.5.2 MRUV . . . . . . . . . . . . . . . 155
2.16. Ejemplo 2.1.5.3 MRUV . . . . . . . . . . . . . . . 157
2.17. Formas de Lanzar un Proyectil . . . . . . . . . . . 160
2.18. Tiro Vertical de un Proyectil, (la l´ ınea puntea-
da del color del proyectil indica la trayectoria de
bajada.) . . . . . . . . . . . . . . . . . . . . . . . 160
2.19. Ejemplo 2.1.6 Tiro Vertical . . . . . . . . . . . . . 162
2.20. Tiro Horizontal. . . . . . . . . . . . . . . . . . . . 169
2.21. Figura para el problema 2.2.1. . . . . . . . . . . . 173
2.22. Gr´fica del Movimiento Parab´lico, mostrando las
a o
velocidades en varios puntos. . . . . . . . . . . . . 174
´
2.23. Envolvente de las Trayectorias Cuyo Angulo de
Disparo est´ Entre 0 y 180o (Par´bola de Seguridad)177
a a
2.24. Ejemplo 2.2.1 Tiro Parab´lico. . . . . . . . . . . . 178
o
2.25. Gr´fica del Movimiento Circular . . . . . . . . . . 183
a
2.26. Velocidad Lineal(v) . . . . . . . . . . . . . . . . . 185
2.27. Diagrama para el ejercicio 2.2.2 . . . . . . . . . . 188
2.28. Aceleraci´n Centr´
o ıpeta . . . . . . . . . . . . . . . 192
2.29. Diagrama para el ejercicio 2.2.2 . . . . . . . . . . 194
2.30. Diagrama para el ejercicio 1 . . . . . . . . . . . . 197
2.31. Diagrama para el ejercicio 2 . . . . . . . . . . . . 198
3.1. Joseph Louis Lagrange, Jean le Rond d’Alembert
y William Rowan Hamilton. . . . . . . . . . . . . 205
3.2. Vector Fuerza . . . . . . . . . . . . . . . . . . . . 206
3.3. Fuerza Puntual . . . . . . . . . . . . . . . . . . . 207
3.4. Fuerzas Distribuidas . . . . . . . . . . . . . . . . 208
3.5. Fuerzas Por su Forma de trabajo . . . . . . . . . 209

13. 3.6. Origen del Rozamiento . . . . . . . . . . . . . . . 214
3.7. Otra Forma en que Actua el Rozamiento sobre
un Cuerpo . . . . . . . . . . . . . . . . . . . . . . 214
3.8. Fuerza Normal . . . . . . . . . . . . . . . . . . . 215
3.9. Fuerza Normal y Rozamiento en un Plano inclinado216
3.10. Diagrama Representando la Fuerza Normal (ej.
3.1.4) . . . . . . . . . . . . . . . . . . . . . . . . . 224
3.11. Diagrama Representando Plano Inclinado (ej. 3.1.4)224
3.12. Acci´n y Reacci´n de la Tercera Ley de Newton . 239
o o
3.13. Figura que muestra las tres leyes de Kepler . . . . 244
3.14. Choque de Dos Cuerpos . . . . . . . . . . . . . . 265
3.15. a.- Una bola en movimiento golpea una bola en
reposo. b.- Colisi´n frontal entre dos bolas en mo-
o
vimiento. c.- Colisi´n de dos bolas que se despla-
o
zan en la misma direcci´n. . . . . . . . . . . . . . 270
o
3.16. Sistema: Cohete y Combustible expulsado para
un intervalo determinado de tiempo. . . . . . . . 275
3.17. Forma de las alas, Cualquiera Funcionan Bien . . 277
3.18. figuras para la Construcci´n del Cohete. . . . . . 278
o
6.1. Funci´n Lineal y = k . . . . . . . . . . . . . . . . 303
o
6.2. Funci´n Lineal y = kx . . . . . . . . . . . . . . . 304
o
6.3. Funci´n Lineal y = kx + b . . . . . . . . . . . . . 304
o
6.4. Funci´n Cuadr´tica y = x2 . . . . . . . . . . . . . 305
o a
1
6.5. Funci´n Inversa y = x . . . . . . . . . . . . . . . 306
o
1
6.6. Funci´n Inversa Cuadr´tica y = x2 . . . . . . . . 306
o a

14. 2 ´
INDICE DE FIGURAS

15. Pr´logo
o
Este trabajo que se presenta, es el fruto de mas de 20 a˜os de
n
experiencia en la ense˜anza de la F´
n ısica a nivel medio superior,
es adecuado al programa de la SEP para el nivel mencionado,
´
inicia con la INTRODUCCION AL CONOCIMIENTO DE LA
F´ISICA, las GENERALIDADES, como la historia de la F´ ısica,
la cual es tan interesante como lo es la lectura de una novela
de misterio, en seguida; La F´ ısica y su Impacto en la Ciencia
y la Tecnolog´ donde se presentan las diferencias entre estos
ıa,
conceptos, luego Los M´todos de Investigaci´n y su Relevancia
e o
en el Desarrollo de la Ciencia, las Magnitudes F´ ısicas y su Medi-
ci´n, las Magnitudes Fundamentales y Derivadas, los Sistemas
o
De Unidades CGS e Ingl´s, El Sistema Internacional de Uni-
e
dades con sus Ventajas y Limitaciones asi tambi´n los M´todos
e e
Directos e Indirectos de Medici´n, la Notaci´n Cient´
o o ıfica y Prefi-
jos presentando algunas formas curiosas de ense˜anza, siguiendo
n
la Transformaci´n de Unidades de un Sistema a Otro, situaci´n
o o
necesaria para entender como se debe medir y aplicar a la vida
diaria.
Al hacer una dosificaci´n del programa, se presenta en es-
o
te punto una autoevaluaci´n par continuar con La precisi´n de
o o
Los Instrumentos en la Medici´n de Diferentes Magnitudes y
o
los tipos de errores, luego contin´a con las cantidades tan im-
u
portantes para la F´ ısica como lo constituyen los Vectores y las

16. 4 Pr´logo
o
Diferencias Entre las Magnitudes Escalares y Vectoriales, las
Caracter´ısticas de los Vectores y su Representaci´n Gr´fica de
o a
los Sistemas de Vectores tales como; Coplanares, no Coplanares,
Deslizantes, Libres Colineales y Concurrentes y su Descomposi-
ci´n y Composici´n de Vectores por M´todos Gr´ficos y Anal´
o o e a ıti-
cos.
En la UNIDAD II se presenta el MOVIMIENTO, primero en
una Dimensi´n situaci´n la cual es la mas sencilla, presentando
o o
los Conceptos de Distancia , Desplazamiento Rapidez, Veloci-
dad, y Aceleraci´n. Los Sistemas de Referencia Absoluto y Re-
o
lativo, y luego, el Movimiento Rectil´
ıneo Uniforme, presentando
en este punto la segunda autoevaluaci´n. Se sigue aqu´ con el
o ı
Movimiento Rectil´ ıneo Uniformemente Variado. la Caida Libre
y el Tiro Vertical as´ como ejemplos del MUA o MRUV Movi-
ı
miento Rectilineo Uniforme Acelerado.
Se contin´a con el MOVIMIENTO EN DOS DIMENSIO-
u
NES, como son: el Tiro Parab´lico Horizontal y Oblicuo, en
o
seguida El Movimiento Circular Uniforme y el Movimiento cir-
cular uniformemente Acelerado.
La Tercera Unidad, presenta los tema sobre las LEYES DE
NEWTON, el TRABAJO, la POTENCIA y para terminar la
ENERG´ Iniciando con las Leyes de Newton, primero con los
IA.
conceptos de FUERZA, sus Tipos y una cantidad importante de
entender y diferenciar con la masa; el Peso de los Cuerpos, luego
u ´
se contin´a con las FUERZAS DE FRICCION, tanto Est´tica a
como din´mica, se contin´a con el enunciado y descripci´n de la
a u o
Primera Ley de Newton o ley de Inercia, importante para enten-
der porque un cuerpo podr´ moverse con Movimiento Rectili-
ıa
neo Uniforme, situaci´n hipot´tica pero necesaria para entender
o e
Porque se mueven los cuerpos.

17. Pr´logo
o 5
El siguiente temas es la Segunda Ley de Newton la cual ex-
plica el porque del movimiento.
En este punto se presenta la tercera autoevaluaci´n por las
o
razones que se mencionaron anteriormente.
Se sigue con la Tercera Ley de Newton o Ley de acci´n y o
Reacci´n concepto que explica porque reacionan las cosas de la
o
manera que sabemos. Sigue con la Ley de Gravitaci´n Universal
o
la cual explica el movimiento planetario.
El Trabajo, la Potencia, y la Energ´ Mec´nica tanto la Po-
ıa a
tencial como la Cin´tica, son los conceptos que se tratan a con-
e
tinuaci´n y luego uno de los principios fundmentales de las leyes
o
de conservaci´n; la “Ley de la Conservaci´n de la Energ´ Para
o o ıa”.
finalizar, se presenta otro principio fundamental de las leyes de
conservaci´n, la “ley de la Conservaci´n del ´
o o Impetu y la Canti-
dad de Movimiento”.
Se termina con la cuarta autovaluaci´n dando fin asi con el
o
curso de “F´ ısica I”, sin dejar de mencionar que est´ en prepara-
a
ci´n el libro de “F´
o ısica II”, libro que se presentar´ en fechas no
a
muy lejanas.
Para las evaluaciones, se hatratdo de encuadrarlas dentro de
las seis categor´ de las competencias gen´ricas del perfil del
ıas e
egresado de la educaci´n medio superior.
o
Antes de dar fin a estas palabras, quiero asumir toda la res-
ponsabilidad por los errores tanto conceptuales como ortogr´fi- a
cos y de cualquier tipo que puedan ser encontrados en estas
l´
ıneas y las que siguen, agradeciendo de antemano cualquier co-
municaci´n al respecto.
o
Neptal´n Z´rate V´squez
ı a a

18. 6 Pr´logo
o

19. Introducci´n al Conocimiento
o
de la F´
ısica
“. . . ofrezco este trabajo como
los principios matem´ticos de la filosof´a,
a ı
pues la tarea mayor de la filosof´a parece consistir en esto:
ı
de los fen´menos del movimiento investigar las fuerzas
o
de la naturaleza, y entonces,
de esas fuerzas, demostrar los otros fen´menos;. . . ”
o
ISAAC NEWTON
Principos Matem´ticos de la Filosof´a Natural.
a ı
Isaac Newton (1642 − 1727) Principia Mathematica.

20. 8 Introducci´n al Conocimiento de la F´
o ısica
1.1. Generalidades
Historia de la F´
ısica.
A˜o
n Evento
624– Thales de Mileto postula que el agua es la susta
547 a. e. c. cia b´sica de la Tierra. Tambi´n estaba enterado de
a e
la fuerza de atracci´n entre imanes y del efecto
o
en el ´mbar, al frotarlo.
a
580– Pit´goras sostuvo que la Tierra era esf´rica.
a e
500 a. e. c. Busc´ una comprensi´n matem´tica del universo.
o o a
500 Anax´goras desafi´ la afirmaci´n de los griegos,
a o o
–428 a. e. c. sobre la creaci´n y destrucci´n de la materia,
o o
ense˜ando que los cambios en la materia se deben
n
a diferentes ordenamientos de part´ ıculas indivisibles
(sus ense˜anzas fueron un antecedente para la ley de
n
conservaci´n de la masa).
o
484– Emp´docles redujo estas partes indivisibles a cuatro
e
424 a. e. c. elementos: tierra, aire, fuego, y agua.
460– Dem´crito desarroll´ la teor´ que el universo est´
o o ıa a
370 a. e. c. formado por espacio vac´ y un n´mero (casi)
ıo u
infinito de part´ıculas invisibles, que se diferencian
unas de otras en su forma, posici´n, y disposici´n.
o o
Toda la materia est´ hecha de part´
a ıculas indivisibles
contin´a en la sig. pag.
u

21. 1.1 Generalidades 9
Historia de la F´
ısica. (continued )
A˜o
n Evento
llamadas ´tomos.
a
384 Arist´teles formaliz´ la recopilaci´n
o o o
–322 a. e. c. del conocimiento cient´ ıfico. Si bien es dif´ se˜alar
ıcil n
como suya una teor´ en particular, el resultado glo-
ıa
bal de esta compilaci´n de conocimientos fue proveer
o
las bases fundamentales de la ciencia por unos mil
a˜os.
n
310– Aristarchus Describe una cosmolog´ id´ntica
ıa e
230 a. e. c. a la propuesta por Cop´rnico 2, 000 a˜os m´s tarde.
e n a
Sin embargo, dado el gran prestigio de Arist´teles,
o
el modelo helioc´ntrico de Aristarchus fue rechazado
e
en favor del modelo geoc´ntrico.
e
287– Arqu´ımedes fue un gran pionero en f´ ısica te´rica.
o
212 a. e. c. Proporcion´ los fundamentos de la hidrost´tica.
o a
70– Ptolomeo de Alejandr´ recogi´ los conocimientos
ıa o
147 e. c. ´pticos de su ´poca. Tambi´n invent´ una compleja teor´
o e e o ıa
del movimiento planetario.
∼ 1000 e. c. Alhazen, ´rabe, produjo 7 libros sobre ´ptica.
a o
1214– Roger Bacon ense˜´ que para aprender los secretos de la
no
1294 e. c. naturaleza, primero debemos observar. Por lo tanto indic´ elo
m´todo con el cual la gente puede desarrollar teor´
e ıas
deductivas, usando las evidencias del mundo natural.
contin´a en la sig. pag.
u

22. 10 Introducci´n al Conocimiento de la F´
o ısica
Historia de la F´
ısica. (continued )
A˜o
n Evento
1473– Nicol´s Cop´rnico impuls´ la teor´ de que la Tierra
a e o ıa
1543 e. c. gira alrededor del sol. Este modelo helioc´ntrico
e
fue revolucionario porque desafi´ el dogma vigente,
o
a causa de la autoridad cient´ıfica de Arist´teles,
o
y caus´ una completa conmoci´n cient´
o o ıfica y filos´fica.
o
1564– es considerado por muchos como el padre
1642 de la f´
ısica moderna, por su preocupaci´n por reemplazar
o
los viejos postulados, en favor de teor´ nuevas,
ıas
deducidas cient´ıficamente. Es famoso por sus teor´ ıas
sobre la mec´nica celeste, y sus trabajos en el ´rea
a a
de la mec´nica, que le abrieron camino a Newton.
a
contin´a en la sig. pag.
u
Historia de la F´
ısica.
A˜o
n Evento
1571– Tycho Brahe y Johannes Kepler. Los datos de los movi-
1630 mientos de objetos celestes muy exactos de Brahe, le
permitieron a Kepler desarrollar su teor´ del movimiento
ıa
planetario el´
ıptico, y proporcionaron una evidencia para el
sistema Copernicano. Adem´s, Kepler escribi´ una descrip-
a o
ci´n cualitativa de la gravitaci´n.
o o
1642– Sir Isaac Newton desarroll´ las leyes de la mec´nica
o a
contin´a en la sig. pag.
u

23. 1.1 Generalidades 11
Historia de la F´
ısica. (continued )
A˜o
n Evento
1727 (la ahora llamada mec´nica cl´sica), que explican el
a a
movimiento de los objetos en forma matem´tica. a
1773– Thomas Young desarroll´ la teor´ ondulatoria de la luz
o ıa
1829 y describi´ la interferencia de la luz.
o
1791– Michael Faraday cre´ el motor el´ctrico, y fue capaz
o e
1867 de explicar la inducci´n electromagn´tica, que proporciona
o e
la primera evidencia de que la electricidad y el magnetismo
est´n relacionados. Tambi´n descubri´ la electr´lisis y descri-
a e o o
bi´ la ley de conservaci´n de la energ´
o o ıa.
1799– Las investigaciones de Joesph Henry sobre inducci´n electro-
o
1878 magn´tica, fueron realizadas al mismo tiempo que las de Fa-
e
´
raday. El construy´ el primer motor; su trabajo con el electro-
o
magnetismo condujo directamente al desarrollo del tel´grafo.e
1873 James Clerk Maxwell realiz´ investigaciones importantes en
o
tres ´reas: visi´n en color, teor´ molecular, y teor´ electro-
a o ıa ıa
magn´tica. Las ideas subyacentes en las teor´ de Maxwell
e ıas
sobre el el electromagnetismo, describen la propagaci´n o
de las ondas de luz en el vac´ ıo.
1874 George Stoney desarroll´ una teor´ del electr´n y estim´
o ıa o o
su masa.
1895 Wilhelm R¨ntgen descubri´ los rayos x.
o o
1898 Marie y Pierre Curie separaron los elementos radioactivos.
contin´a en la sig. pag.
u

24. 12 Introducci´n al Conocimiento de la F´
o ısica
Historia de la F´
ısica. (continued )
A˜o
n Evento
1898 Joseph Thompson midi´ el electr´n, y desarroll´ su modelo
o o o
“de la torta con pasas” del ´tomo - dice que el ´tomo
a a
es una esfera con carga positiva uniformemente distribuida,
con peque˜os electrones negativos como pasas adentro.
n
1900 Max Planck sugiri´ que la radiaci´n est´ cuantificada
o o a
(aparece en cantidades discretas).
1905 Albert Einstein, uno de los pocos cient´ ıficos que tom´ o
en serio las ideas de Planck; propuso un cuanto de luz
(el fot´n) que se comporta como una part´
o ıcula. Sus otras
teor´ explicaronla equivalencia entre la masa y la energ´
ıas ıa,
la dualidad part´ıcula-onda de los fotones, el principio de
equivalencia, y especialmente la relatividad del espacio tiempo.
1909 Hans Geiger y Ernest Marsden, bajo la supervisi´n de Ernest
o
Rutherford, dispersaron part´ ıculas alfa mediante una hoja de
oroy observaron grandes ´ngulos de dispersi´n; sugirieron que
a o
los ´tomos tienen un n´cleo peque˜o y denso, cargado positi-
a u n
vamente.
1911 Ernest Rutherford infiri´ la existencia del n´cleo como resulta-
o u
do de la dispersi´n de las part´
o ıculas alfa en el experimento
realizado por Hans Geiger y Ernest Marsden.
1912 Albert Einstein explic´ la curvatura del espacio-tiempo.
o
1913 Niels Bohr tuvo ´xito al construir una teor´ de la estructura
e ıa
contin´a en la sig. pag.
u

25. 1.1 Generalidades 13
Historia de la F´
ısica. (continued )
A˜o
n Evento
at´mica, bas´ndose en ideas cu´nticas.
o a a
1919 Ernest Rutherford encontr´ la primer evidencia de un prot´n.
o o
1921 James Chadwick y E.S. Bieler concluyeron que alguna fuerzas
fuertes tienen que mantener unido el n´cleo.
u
1923 Arthur Compton descubri´ la naturaleza cu´ntica (part´
o a ıcula)
de los rayos x, confirmando de este modo al fot´n o
como part´ ıcula.
1924 Louis de Broglie propuso que la materia tiene propiedades
ondulatorias.
1925 Wolfgang Pauli formul´ el principio de exclusi´n para
o o
(enero) los electrones de un ´tomo.
a
1925 Walther Bothe y Hans Geiger demostraron que la energ´ ıa
(Abril) y la masa se conservan en los procesos at´micos.
o
1926 Erwin Schr¨dinger desarroll´ la mec´nica ondulatoria, que
o o a
describe el comportamiento de sistemas cu´nticos constituidos
a
por bosones. Max Born le di´ una interpretaci´n probabil´
o o ıstica
a la mec´nica cu´ntica. G.N. Lewis propuso el nombre de
a a
“fot´n” para el cuanto de luz.
o
1927 Se observ´ que ciertos materiales emiten electrones (decai-
o
miento beta). Dado que ambos, el ´tomo y el n´cleo, tienen
a u
niveles discretos de energ´ es dif´ entender por qu´ los
ıa, ıcil e
electrones producidos en esta transici´n, pueden tener un
o
contin´a en la sig. pag.
u

26. 14 Introducci´n al Conocimiento de la F´
o ısica
Historia de la F´
ısica. (continued )
A˜o
n Evento
espectro continuo (vea 1930 para tener una respuesta).
1927 Werner Heisenberg formul´ el principio de incertidumbre:
o
cuanto m´s sabe ud. sobre la energ´ de una part´
a ıa ıcula, menos
sabr´ sobre el tiempo en el que tiene esa energ´ (y vice versa.)
a ıa
La misma incertidumbre se aplica al ´ ımpetu y la coordenada.
1928 Paul Dirac combin´ la mec´nica cu´ntica y la relatividad
o a a
especial para describir al electr´n.
o
contin´a en la sig. pag.
u
Historia de la F´
ısica.
A˜o
n Evento
1930 La mec´nica cu´ntica y la relatividad especial est´n bien
a a a
establecidas. Hay tres part´
ıculas fundamentales: protones,
electrones, y fotones. Max Born, despu´s de tomar conocimiento
e
de la ecuaci´n de Dirac, dijo, “La f´
o ısica, como la
conocemos, ser´ obsoleta en seis meses.”
a
1930 Wolfgang Pauli sugiri´ el neutrino para explicar el espectro
o
continuo de los electrones en el decaimiento beta.
1931 Paul Dirac comprendi´ que las part´
o ıculas cargadas positivamente
requeridas por su ecuaci´n eran nuevos objetos (el los llam´
o o
“positrones”). Son exactamente como electrones, pero cargados
positivamente. Este es el primer ejemplo de antipart´ ıculas.
contin´a en la sig. pag.
u

27. 1.1 Generalidades 15
Historia de la F´
ısica. (continued )
A˜o
n Evento
1931 James Chadwick descubri´ el neutr´n. Los mecanismos de las
o o
uniones nucleares y los decaimientos se convirtieron en problemas
principales.
1933– Enrico Fermi desarroll´ una teor´ del decaimiento beta, que
o ıa
e ´
1934 introdujo las interacciones d´biles. Esta es la primera teor´ ıa
que usa expl´ ıcitamente los neutrinos y los cambios de sabor
de las part´ıculas.
Hideki Yukawa combin´ la relatividad y la teor´ cu´ntica,
o ıa a
para describir las interacciones nucleares sobre la base del
intercambio, entre protones y neutrones, de nuevas part´ ıculas
(mesones llamados “piones”). A partir del tama˜o del n´cleo,
n u
Yukawa concluy´ que la masa de las supuestas part´
o ıculas (meso-
´
nes) es superior a la masa de 200 electrones. Este es el
comienzo de la teor´ mes´nica de las fuerzas nucleares.
ıa o
1937 Una part´ ıcula con una masa de 200 electrones es descubierta
en los rayos c´smicos. Mientras que al principio, los f´
o ısicos
pensaron que era el pi´n de Yukawa, se descubri´ m´s
o o a
tarde que era un mu´n.o
1938 E.C.G. Stuckelberg observ´ que los protones y
o
los neutrones no decaen hacia ninguna combinaci´n de o
electrones, neutrinos, muones, o sus antipart´ ıculas.
La estabilidad del prot´n no puede ser explicada en t´rminos
o e
contin´a en la sig. pag.
u

28. 16 Introducci´n al Conocimiento de la F´
o ısica
Historia de la F´
ısica. (continued )
A˜o
n Evento
de conservaci´n de energ´ o de carga; propuso la conservaci´n
o ıa o
independiente del n´mero de part´
u ıculas pesadas.
1941 C. M¨ller y Abraham Pais introdujeron el termino “nucle´n”
o o
como un t´rmino gen´rico para los protones y los neutrones.
e e
1946– Los f´ısicos comprendieron que la part´ ıcula del rayo c´smico,
o
1947 que se pensaba que era el mes´n de Yukawa, es en cambio un
o
“mu´n”, la primer part´
o ıcula en ser encontrada, de las
de la segunda generaci´n de part´
o ıculas materiales. Este descu-
brimiento fue completamente inesperado –I. I. Rabi coment´ o
“¿qui´n orden´ ´sto?”– El t´rmino“lept´n” se introdujo para
e oe e o
describir objetos que no interactuan demasiado fuerte
(los electrones y los muones son leptones).
1947 En los rayos c´smicos es encontrado un mes´n, que interact´a
o o u
fuertemente, y se determina que es un pi´n. o
1947 Los f´ ısicos desarrollan procedimientos para calcular las pro-
piedades electromagn´ticas de los electrones, positrones,
e
y fotones. Se introducen los diagramas de Feynman.
1948 El sincro-ciclotr´n de Berkeley produce los primeros piones
o
artificiales.
1949 Enrico Fermi y C.N. Yang sugieren que un pi´n es una estruc-
o
tura compuesta por un nucle´n y un antinucle´n. Esta idea de
o o
part´ıculas compuestas es completamente revolucionaria.
contin´a en la sig. pag.
u

29. 1.1 Generalidades 17
Historia de la F´
ısica. (continued )
A˜o
n Evento
Descubrimiento de K+ v´ sus decaimientos.
ıa
1950 Es descubierto el pi´n neutro.
o
1951 Se descubren dos nuevos tipos de part´ ıculas en los rayos c´smicos.
o
Son descubiertas mientras se observan unas trazas en forma de V;
se las descubre al reconstruir los objetos el´ctricamente neutros,
e
que ten´ que haber deca´
ıan ıdo, para producir los dos objetos carga-
dos, que dejaron las trazas. Las part´ ıculas fueron llamadas la
λ0 y la κ0 .
1952 Descubrimiento de la part´ ıcula delta: eran cuatro part´ ıculas
similares (δ++ , δ+ , δ0 , y δ− .)
1952 Donald Glaser invent´ la c´mara de burbujas. Comienza a operar
o a
el Cosmotr´n de Brookhaven, un acelerador de 1,3 GeV.
o
1953 El comienzo de la “explosi´n del n´mero de part´
o u ıculas” -una
verdadera proliferaci´n de part´
o ıculas.
1953– La dispersi´n de electrones por un n´cleo, revela una dis-
o u
1957 tribuci´n de la densidad de carga dentro de los protones, y
o
neutrones. La descripci´n de esta estructura electromagn´tica
o e
de los protones y neutrones, sugiere cierta estructura interna
en estos objetos; a pesar de eso se los sigue considerando como
part´ıculas fundamentales.
contin´a en la sig. pag.
u

30. 18 Introducci´n al Conocimiento de la F´
o ısica
Arist´teles
o Arquimedes Ticho Brahe
Jhoannes Kepler Nicol´s Copernico
a Galileo Galilei
Figura 1.1: Sabios de la Antig¨edad.
u

31. 1.1 Generalidades 19
Max Planck Niels Bohr & Alberto Einstein Louis de Broglie
Erwin Schr¨dinger
o Werner Heisenberg en 1927 Richard Feynman
Figura 1.2: Cient´
ıficos de la Mec´nica Cu´ntica.
a a

32. 20 Introducci´n al Conocimiento de la F´
o ısica
P. A. M. Dirac Enrico Fermi Abdus Salam
Sheldon Glashow Steven Weinberg Richard Feynman 1947.
Figura 1.3: Cient´
ıficos de loa Quarks.

33. 1.1 Generalidades 21
Historia de la F´
ısica.
A˜o
n Evento
1954 C.N. Yang y Robert Mills desarrollan un nuevo tipo de teor´ ıa,
llamada “teor´ de calibre (o de Gauge).” Aunque no
ıas
fueron aceptadas en ese momento, este tipo de teor´ ıas
constituyen actualmente la base del Modelo Standard.
1957 Julian Schwinger escribe un trabajo proponiendo la unificaci´n o
de las interacciones d´biles y electromagn´ticas.
e e
1957– Julian Schwinger, Sidney Bludman, y Sheldon Glashow, en
1959 trabajos separados, sugieren que todas las interacciones
d´biles son mediadas por bosones pesados cargados, m´s tarde
e a
llamados W+ y W− . Realmente, Yukawa fue el primero en suge-
rirlo (veinte a˜os antes). El hab´ propuesto al pi´n como el me-
n ıa o
diador de las fuerzas d´biles, propiciando el intercambio de bosones.
e
1961 A medida que el n´mero de part´
u ıculas conocidas se incremen-
taba, el grupo SU(3), un esquema de clasificaci´n matem´tico
o a
para organizar las part´ıculas, ayud´ a los f´
o ısicos a reconocer
patrones en los tipos de part´ıculas.
1962 Los experimentos verificaron que existen dos tipos distintos de
o o ´
neutrinos (neutrinos electr´n y neutrinos mu´n). Esto ya hab´ ıa
sido inferido, por consideraciones te´ricas.
o
1964 Murray Gell-Mann y George Zweig introdujeron la idea tentativa
de los quarks. Sugirieron que los mesones y los bariones est´n a
compuestos por quarks o antiquarks de tres tipos, llamados up,
contin´a en la sig. pag.
u

34. 22 Introducci´n al Conocimiento de la F´
o ısica
Historia de la F´
ısica. (continued )
A˜o
n Evento
down y strange (u, d, s), con spin 1 y cargas el´ctricas 3 , − 1 , − 3 ,
2 e 2
3
1
respectivamente (resulta que esta teor´ no es compl´tamente
ıa e
exacta). Ya que estas cargas nunca han sido observadas,
la introducci´n de los quarks fue tratada como una explicaci´n
o o
matem´tica de los patrones de sabor, seguidos por las masas de
a
las part´ıculas, m´s que como un postulado de existencia de
a
objetos f´ısicos reales. M´s tarde, los desarrollos te´ricos
a o
y experimentales, nos permitieron considerar a los quarks
como objetos f´ ısicos reales, aunque no puedan ser aislados.
1964 Ya que los leptones ten´ cierto patr´n, varios tra-
ıan o
bajos sugirieron la existencia de un cuarto quark, con otro
sabor, para que el patr´n de los quarks sea similar al de los
o
leptones; actualmente los sabores se llaman generaciones de
materia. Muy pocos f´ ısicos tomaron seriamente esta sugerencia en
ese momento. Sheldon Glashow y James Bjorken acu˜aron el n
t´rmino “charm” (encanto) para el cuarto (c) quark.
e
1965 O.W. Greenberg, M.Y. Han, y Yoichiro Nambu introdujeron la
propiedad de carga de color del quark. Todos los hadrones
observados son de color neutro.
1966 El modelo del quark es aceptado en forma relativamente lenta,
debido a que los quarks no han sido observados.
1967 Steven Weinberg y Abdus Salam separadamente propusieron
contin´a en la sig. pag.
u

35. 1.1 Generalidades 23
Historia de la F´
ısica. (continued )
A˜o
n Evento
una teor´ que unifica las interacciones electromagn´ticas y
ıa e
d´biles formando la interacci´n electrod´bil. Sus teor´
e o e ıas
requieren la existencia de un bos´n neutro, que interact´a
o u
en forma d´bil (ahora llamado el Z0 ) y que sea el mediador
e
de la interacci´n d´bil; ese bos´n no hab´ sido observado
o e o ıa
a´n en aquel tiempo. Ellos tambi´n predijeron la existencia
u e
de un bos´n, masivo, adicional, llamado el bos´n de Higgs que
o o
ha sido observado hasta el a˜o 1995.
n
. 1968– En el Acelerador Lineal de Stanford, en un experimento
1969 en el cual se hace que los electrones sean dispersados por
protones, los electrones parecen “rebotar”contra un peque˜o n
centro duro dentro del prot´n. James Bjorken y Richard
o
Feynman analizaron estos datos en t´rminos de un
e
modelo de part´ ıculas constituyentes dentro del prot´n (ellos no
o
usaron el nombre “quark” para los constituyentes aunque
este experimento proporcion´ evidencia para los quarks.)
o
1970 Sheldon Glashow, John Iliopoulos, y Luciano Maiani recono-
cieron la importancia cr´ ıtica de un cuarto tipo de quark en el
contexto del Modelo Standard. Un cuarto quark permite
una teor´ que tiene interacciones d´biles mediadas por un Z0 ,
ıa e
con cambio de sabor.
1973 Donald Perkins, estimulado por una predicci´n del Modelo
o
contin´a en la sig. pag.
u

36. 24 Introducci´n al Conocimiento de la F´
o ısica
Historia de la F´
ısica. (continued )
A˜o
n Evento
Standard, volvi´ a analizar algunos datos viejos del CERN y
o
encontr´ indicadores de interacciones debiles sin intercambio
o
de carga de color (debida al intercambio de un Z0 .)
1973 Fue formulada una teor´ cu´ntica de campos, para las
ıa a
interacciones fuertes. Esta teor´ de quarks y gluones (que
ıa
ahora es parte del Modelo Standard) es similar, en su estruc-
tura, a la electrodin´mica cu´ntica (QED), pero dado que las
a a
teor´ se llama interacciones fuertes act´an sobre las cargas
ıa u
de color, esta cromodin´mica cu´ntica (QCD). Los quarks est´n
a a a
destinados a ser part´ ıculas reales, con una carga de color.
Los gluones son los cuantos, sin masa, del campo de las
interacciones fuertes. Esta teor´ de interacciones fuertes fue
ıa
primero sugerida por Harald Fritzsch y Murray Gell-Mann.
1973 David Politzer, David Gross, y Frank Wilczek descu-
brieron que la teor´ de color de las interacciones fuertes
ıa
tiene una propiedad especial, hoy llamada “libertad
asint´tica.” Esta propiedad es necesaria para describir los datos
o
de 1968 − 1969 en relaci´n con el prot´n.
o o
1974 En una conferencia, John Iliopoulos present´, por primera
o
vez en un unico reporte, la visi´n de la f´
´ o ısica ahora llamada el
Modelo Standard.
1974 Burton Richter y Samuel Ting, liderando experimentos
contin´a en la sig. pag.
u

37. 1.1 Generalidades 25
Historia de la F´
ısica. (continued )
A˜o
n Evento
(Nov.) independientes, anunciaron el mismo d´ su descubrimiento
ıa
de la misma nueva part´ ıcula. Ting y sus colaboradores en
Brookhaven llamaron a esta part´ ıcula la part´
ıcula “J”,
mientras que Richter y sus colaboradores en SLAC llamaron
a esta part´
ıcula la part´ıcula ψ. Ya que los descubrimientos
tuvieron igual importancia, la part´ ıcula es conocida com´n-u
mente como la part´ ıcula J/ψ. La part´ ıcula J/ψ es
un mes´n charm-anticharm.
o
1976 Gerson Goldhaber y Francois Pierre encontraron el mes´n D0 (y o
los quarks antiup y charm). Las predicciones te´ricas concordaron
o
dram´ticamente con los resultados experimentales, ofreciendo un
a
fuerte soporte al Modelo Standard.
1976 El lept´n τ fue descubierto por Martin Perl y sus colaboradores
o
en SLAC. Ya que este lept´n es la primer part´
o ıcula registrada
de la tercera generaci´n, fue completamente inesperado.
o
1977 Leon Lederman y sus colaboradores en el Fermilab descubrieron
sin embargo otro quark (y su antiquark). Este quark fue llamado
el quark “bottom”. Ya que los f´ ısicos se imaginaban
que los quarks ven´ en pares, este descubrimiento incentiv´ la
ıan o
b´squeda del sexto quark -“top.”
u
1978 Charles Prescott y Richard Taylor observaron una interacci´n o
d´bil mediada por un Z0 , en la dispersi´n por deuterio, de
e o
contin´a en la sig. pag.
u

38. 26 Introducci´n al Conocimiento de la F´
o ısica
Historia de la F´
ısica. (continued )
A˜o
n Evento
electrones polarizados, en la que aparece una violaci´n de la
o
conservaci´n frente a paridad, como lo predijo el Modelo
o
Standard y confirmando as´ la predicci´n te´rica.
ı o o
1979 Se encuentra en PETRA una fuerte evidencia de un glu´n o
radiado por un quark o antiquark iniciales. PETRA es una
facilidad de colisi´n de haces del laboratorio DESY en Hamburgo.
o
1983 Los bosones intermediarios, Wn y el Z0 , requeridos por la teor´
˜ ıa
electrod´bil, son observados en dos experimentos que usan el
e
sincrotr´n del CERN y que emplean las t´cnicas desarrolladas por
o e
Carlo Rubbia y Simon Van der Meer para colisionar protones y
antiprotones.
1989 Los experimentos llevados a cabo en SLAC y en CERN sugirieron
fuertemente que hay tres y s´lo tres generaciones de part´
o ıculas
´
fundamentales. Esto se infiere de la observaci´n que el tiempo de
o
vida del bos´n Z0− , s´lo es consistente con la existencia de
o o
exactamente tres neutrinos muy livianos (o sin masa).
1995 Despu´s de dieciocho a˜os de b´squeda en muchos aceleradores, los
e n u
experimentos CDF y D0 en el Fermilab descubrieron el quark top
o bos´n de Higgs con una masa inesperada de 175 GeV.
o
Nadie entiende por qu´ la masa es tan diferente de la de los otros
e
cinco quarks.
1996 Se observa el 5o estado de la materia.
contin´a en la sig. pag.
u

39. 1.1 Generalidades 27
DEFINICIONES
CIENCIA.
Conjunto de conocimientos ordenados, sistema-
tizados y jerarquizados.
La parte mas importante de la ciencia, consiste en aplicar
los m´todos que se utilizan para producir conocimientos, es una
e
forma de pensar y un c´mulo de conocimientos.
u
F´
ISICA.
F´ısica (del griego ϕ`ςικ´ physike: naturaleza).
υ ε
Ciencia que se encarga del estudio de la materia,
la energ´ y las interrelaciones que suceden entre
ıa
ellas.
El significado de estudiar es; investigar, analizar
y concluir.
La propiedades se refieren a las caracter´
ısticas
que definen la energ´ y la materia.
ıa
Para un mejor entendimiento de la F´
ısica, se propone seguir
el procedimiento siguiente:

40. 28 Introducci´n al Conocimiento de la F´
o ısica
´
Paso 1. Explicar Como suceden los fen´menos. Ambito
o
Conceptual.
Paso 2. Ejemplificar la medici´n cuantitativa (ma-
o
´
tem´tica) del cuanto sucede. Ambito procedi-
a
mental.
´
Paso 3. La explicaci´n del Porque sucede. Ambito Con-
o
ceptual y procedimental.
El objeto del estudio de la F´
ısica es el de poder
comprender y explicar los fen´menos que acontecen
o
a nuestro alrededor y que todos los dias podemos
observar.
Lo anterior mediante un proceso adecuado de evaluaci´n,o
podr´ ser tomado como la evidencia de la Competencia.[1]
a
Divisi´n de la F´
o ısica para su Estudio.
Esta divisi´n consta de dos partes:
o
F´
ısica Cl´sica
a
La que a su vez se divide en:
1. Mec´nica.
a
2. termolog´
ıa.

41. 1.1 Generalidades 29
3. Ondas.
´
4. Optica.
5. Magnetismo
6. Electricidad
F´
ısica Moderna
Que consta del Estudio del:
1. N´cleo
u
´
2. Atomo
3. Mol´culas
e

42. 30 Introducci´n al Conocimiento de la F´
o ısica
Actividad. 3.1.7.1
1. Realice una investigaci´n sobre: Divisi´n de la F´
o o ısica para
su Estudio.
2. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
3. Con base en la investigaci´n realizada escriba por lo menos
o
dos de las definiciones de cada una de las partes de la F´
ısica.
4. para la evaluaci´n se tomar´ en cuenta:
o a
a) Entrega en tiempo y forma (una semana m´ximo).
a
b) Claridad en las definiciones presentadas.
c) Coherencia de lo escrito.
d) Validez y pertinencia de las ideas expuestas (que tenga
relaci´n con la situaci´n actual).
o o
e) Presentaci´n.
o
f ) Profundidad del escrito.
5. Escriba en los espacios correspondientes de este libro, las
definiciones mas adecuadas para las diferentes partes de la
f´
ısica.
Materia Estado y Propiedades.
Materia: Todo lo existente en la naturaleza y
ocupa un lugar en el espacio.
Estado: Forma, manera en que se encuentra la
materia.

43. 1.1 Generalidades 31
Figura 1.4: Propiedades de la Materia.

44. 32 Introducci´n al Conocimiento de la F´
o ısica
S´lido
o
L´
ıquido
Gas
Plasma
Condensado de Bose Einsten
Actividad. 1.1.2
1. Realice una investigaci´n sobre: Los Estados de la Materia.
o
2. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
3. Con base en la investigaci´n realizada escriba un ensayo so-
o
bre los estados de la materia.
4. Para la evaluaci´n de la actividad se tomar´ en cuenta:
o a
a) Entrega en tiempo y forma (una semana m´ximo).
a
b) Claridad.
c) Coherencia.
d) Validez y pertinencia de las ideas expuestas.
e) Profundidad de los conceptos.
f) Presentaci´n.
o
g) Profundidad del escrito.
5. Como colof´n, escriba en los espacios correspondientes de
o
este libro, las definiciones que resulten mas adecuadas para
los diferentes Estados de la Materia.
Propiedades: Son las Caracter´
ısticas de la ma-
teria

45. 1.1 Generalidades 33
Pueden seer: Generales y particulares.
Algunas de las generales son:
Masa: Es la cantidad de materia que contiene
un cuerpo y se mide en kilogramos [kg].
Peso: Fuerza de atracci´n que ejerce la tierra
o
sobre la materia, se mide en Newtons [N ].
Volumen: Espacio que ocupa un cuerpo, se mide
en metros c´bicos [m3 ].
u
Una propiedad que algunos autores consideran particular es
la:
Densidad: cociente entre la masa y el volumen
kg
de un cuerpo. m3 .
m kg
d=̺= (1.1)
V m3
1 litro=1000 cm3
1 ml=1 cm3

46. 34 Introducci´n al Conocimiento de la F´
o ısica
Actividad. 1.1.3
1. Realice una investigaci´n sobre: Las Propiedades de la Ma-
o
teria.
2. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
3. Con base en la investigaci´n realizada dibuje un mapa men-
o
tal personal sobre Los Estados de la Materia.
4. Reunirse en equipo y realizar un mapa conceptual grupal.
5. Analizar el mapa conceptual grupal de forma individual.
6. para la realizaci´n del mapa personal y grupal tomar en
o
cuenta:
a) ¿Cuales son los conceptos mas importantes?.
b) ¿Est´n expuestos los conceptos mas importantes en el
a
mapa?.
c) ¿Las ligas (flechas) son suficientes?
d ) ¿Existe jerarqu´ y uniones cruzadas suficientes?.
ıa
e) ¿Se encuentra actualizada la informaci´n?.o
f ) Para el nivel del curso justificar la Profundidad del ma-
pa.
7. Reunirse nuevamente, realizar un mapa mental final.

47. 1.1 Generalidades 35
Para la evaluaci´n de la actividad 1.1.3 se tomar´ en cuenta:
o a
1. Entrega en tiempo y forma (una semana m´ximo).
a
2. Claridad en los Mapas presentados.
3. Coherencia.
4. Validez y pertinencia de las ideas expuestas.
5. Profundidad de los conceptos.
6. Presentaci´n al grupo por el coordinador.
o
7. Obtenci´n de un mapa conceptual grupal final.
o
8. Una conclusi´n importante es contestar si: ¿La densidad es
o
una propiedad general o particular?
Ejemplo: 1.1 Se midi´ un cubo de hierro de 1cm de lado siendo
o
su masa de 7,8 gramos ¿cual es la densidad del hierro?, calcu-
lando su volumen.
a). Diagrama; se presenta en la fig 1.5
Figura 1.5: Representaci´n de un Cubo de Hierro para el Ejemplo 1.1.
o
b). ¿Cual es su masa (m)?
m = 7.8 g
pero esta se necesita en kilogramos (kg) por lo que hay que
realizar la conversi´n.
o

48. 36 Introducci´n al Conocimiento de la F´
o ısica
Se sabe que 1 kg = 1000 g
7,8g 1kg 7,8g kg
/ 0,0078kg
= =
1 1000g 1000g / 1
c). ¿Cual es la longitud (l) del lado del cubo?
l = 1cm
Pero en el sistema internacional, las longitudes se miden
en metros por lo que se debe realizar la conversi´n de las
o
unidades de medida; sabiendo que 1 m= 100 cm.
1cm 1m 1cm m
ր 0,01m
= = = 0,01m
1 100cm 100cm
ր 1
d). Se calcula el volumen (V )
V = l3
V = (0,01m)3
= (0,01m)(0,01m)(0,01m)
= (0,01)(0,01)(0,01)(m)(m)(m)
V = 0,000001m3
e). ¿Cual la densidad?
Mediante la relaci´n 1.1
o
m kg
D=̺=
V m3
m 0,0078kg
̺= =
V 0,000001m3
kg
̺ = 7800 3
m
kg
La densidad (̺) es 7800 m3

49. 1.1 Generalidades 37
Fen´meno F´
o ısico y Relaciones con Otros Fen´menos Naturales.
o
Fen´meno: Suceso que ocurre en la naturaleza.
o
Ejemplos.
Un eclipse de sol o luna.
Vaciar agua en un recipiente.
La lluvia, etc.
F´
ısico: sucede cuando no se alteran las propie-
dades del objeto que sufre el fen´meno.
o
Ej. Corte de papel.
Qu´ ımico: cuando existe una reacci´n qu´
o ımica
y los ´tomos y mol´culas se reacomodan.
a e
Ej. Quemar papel
Biol´gicos: cuando existe una combinaci´n de
o o
fen´menos fisicos y qu´
o ımicos.
Es decir que se afectan sus propiedades y sufre una reacci´n
o
qu´
ımica.
Ej. Crecimiento de un arbol.

50. 38 Introducci´n al Conocimiento de la F´
o ısica
Micromundo.
Se refiere a los
fen´menos f´
o ısicos que se presentan a nivel
at´mico.
o
De manera sencilla el ´tomo est´ constituido por cuarks, los
a a
cuales cuando se unen forman electrones, protones y neutrones,
los electrones tienen carga negativa, los protones carga positiva,
los neutrones sin carga, la masa es similar a la del prot´n y es
o
de aproximadamente
mn = mp = 0,00000000000000000000000000166kg = 1,66×10−27 kg
El electr´n tiene una masa de
o
me = 0,000000000000000000000000000000911kg. = 9,11×10−31 kg
Figura 1.6: Mapa Conceptual de Fen´meno
o

51. 1.1 Generalidades 39
El prot´n tiene carga positiva(+) y el electr´n tiene carga
o o
negativa (−) El valor de la carga tanto del electr´n como del
o
proton es de:
−qe = qp = 0,00000000000000000016C(oulombs) = 1,6×10−19 C
De aqu´ se observa porque se habla del Micromundo, porque
ı
los valores con que se miden sus propiedades son muy peque˜os.
n
La notaci´n que se muestra al final del valor dado, se conoce
o
como notaci´n Cient´
o ıfica, pero aqu´ se le llama notaci´n “com-
ı o
pacta”, porque es mas sencilla que el valor con varios ceros.
Macromundo.
fen´menos f´
o ısicos que se presentan a nivel mu-
cho mayor que las dimensiones at´micas.
o
El micromundo constituye al macromundo cuando forma
´tomos, mol´culas, compuestos, cuerpos, planetas, estrellas, sis-
a e
temas solares, galaxias, y el universo. p. e. La masa de la tierra
es:
mT = 5980000000000000000000000.kg = 5,98 × 1024 kg
y aqui se observa que los valores con que se miden sus propie-
dades son muy grandes, por lo que constituyen al macromundo.
Tanto el macromundo como el micromundo, est´n unidos por
a
fuerzas, las cuales rigen en ciertas condiciones; estas fuerzas son:
El ´tomo est´ unido por fuerzas el´ctricas (fuerza de Coulomb).
a a e

52. 40 Introducci´n al Conocimiento de la F´
o ısica
El universo (Macromundo), est´ unido por la fuerza gra-
a
vitacional.
La fuerza nuclear, la cual es de corto alcance, mantiene
unidos a los protones y neutrones en el n´cleo.
u
La fuerza d´bil es la responsable de la radiactividad.
e
Figura 1.7: Tipos de Fuerza en la Naturaleza.
Figura 1.8: Componentes de la Materia

53. 1.1 Generalidades 41
1.1.1. La F´ısica y su Impacto en la Ciencia y la Tec-
nolog´ıa.
El objetivo de la ciencia es:
Responder preguntas mas que nada te´ricas, pa-
o
ra que despu´s de observar hechos, fen´menos y su
e o
relaci´n con la naturaleza, expresar teor´
o ıas.
Por otra parte, la tecnolog´
ıa:
Son generalmente m´todos para resolver proble-
e
mas pr´cticos. Herramientas t´cnicas y procesos en
a e
los cuales se aplican los descubrimientos de la cien-
cia.
La uni´n de la ciencia y la tecnolog´ da como resultado be-
o ıa,
neficios para la sociedades es decir se proyecta, se dise˜a y se
n
crea.
1.1.2. Los M´todos de Investigaci´n y su Relevancia
e o
en el Desarrollo de la F´
ısica.
M´todo Cient´
e ıfico.
Para poder Investigar o crear conocimiento, hay que apli-
car un procedimiento o m´todo, el cual para la ciencia se conoce
e
como: Metodo Cient´ ıfico, este es un conjunto de pasos a seguir
para llegar a una conclusi´n sobre un fen´meno.
o o

54. 42 Introducci´n al Conocimiento de la F´
o ısica
Figura 1.9: Diagrama de flujo del M´todo Cient´
e ıfico.

55. 1.1 Generalidades 43
Procedimiento para Aplicar el Metodo Cient´
ıfico.
Paso 1. Planteamiento de un problema
Paso 2. Investigaci´n preeliminar del fen´meno. (puede
o o
ser en libros, internet, encuesta, etc.)
Paso 3. Observaci´n del fen´meno. Que sucede, como
o o
sucede, etc.
Paso 4. Hip´tesis. Posible explicaci´n del fen´meno
o o o
Paso 5. Experimentaci´n. Repetici´n del fen´meno
o o o
(cuantas veces sea necesario) en condiciones fa-
vorables.
Paso 6. Contrastar los resultados experimentales con la
hip´tesis formulada.
o
Paso 7. Si los resultados explican el fen´meno, se com-
o
prueba la hip´tesis.
o
Paso 8. Si no se comprueba la hip´tesis, esta debe re-
o
formularse (nueva hip´tesis) y repetir desde el
o
paso n´mero 3.
u
Paso 9. Si se cumple la hip´tesis y se explica el
o
fen´meno, se enuncia una ley.
o
Aqui es necesario clarificar los conceptos de ley y teor´ ya
ıa,
que estos en algunos casos, se toman como sin´nimo.
o

56. 44 Introducci´n al Conocimiento de la F´
o ısica
Ley: regla y norma constante e invariable que
rige los fen´menos de la naturaleza.[27]
o
Teor´ Serie de leyes que sirven para relacionar
ıa:
determinado orden de fen´menos.[27]
o
Por lo que hay que remarcar que una Teor´ es un conjunto
ıa
de leyes.
Actividad. 1.1.2.1
1. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
2. Democr´ticamente, escoja uno de los siguientes temas.
a
a) Autodeterminaci´n y cuidado de uno mismo.
o
b) Expresi´n y comunicaci´n.
o o
c) Aprendisaje aut´nomo.
o
d) Participaci´n en la sociedad con responsabilidad.
o
e) El trabajo en forma colaborativa.
f) Pensamiento critico y reflexivo.
3. Aplicar al tema el Metodo Cient´
ıfico.

57. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 45
Para la evaluaci´n de la actividad 1.1.2.1 se tomar´ en cuenta:
o a
1. Entrega en tiempo y forma (dos semanas m´ximo).
a
2. Claridad en las definiciones presentadas.
3. Coherencia de lo escrito.
4. Profundidad del escrito.
5. Presentaci´n ante el grupo mediante un debate.
o
6. Validez y pertinencia de las ideas expuestas (que tenga rela-
ci´n con la situaci´n actual).
o o
7. Se aplicar´ una coevaluaci´n con los integrantes de los equi-
a o
pos. Ponerse de acuerdo con el profesor.
1.2. Magnitudes F´
ısicas y su Medici´n.
o
Introducci´n
o
La existencia de gran n´mero de diversas unidades, creaba
u
dificultades en las relaciones internacionales de comercio, en el
intercambio de resultados de investigaciones cient´ ıficas, etc. Co-
mo consecuencia los cient´ ıficos de diversos pa´ intentaron es-
ıses
tablecer unidades comunes, v´lidas en todos ellos.
a
Durante la Revoluci´n Francesa se cre´ el Sistema M´tri-
o o e
co Decimal que, seg´n sus autores, deber´ servir en todos los
u ıa
tiempos, para todos los pueblos, para todos los pa´ ıses. Su ca-
racter´
ıstica principal es que las distintas unidades de una mis-
ma magnitud se relacionan entre s´ como exponentes enteros de
ı
diez.
Desde mediados del siglo XIX, el sistema m´trico comenz´ a
e o
difundirse ampliamente, fue legalizado en todos los pa´ y cons-
ıses
tituye la base de las unidades que sirven para la medici´n de o

58. 46 Introducci´n al Conocimiento de la F´
o ısica
diversas magnitudes en la F´ısica, en otras ciencias y en la inge-
nier´
ıa.
Algunos estudiantes recuerdan haber o´ a sus padres o
ıdo
abuelos acerca de las unidades propias de su lugar de origen,
pero no suelen conocer su definici´n. Mediante algunos ejemplos
o
ilustrativos se puede poner de manifiesto la necesidad de dispo-
ner de unidades de medida que tengan un ´mbito de aplicaci´n
a o
lo m´s amplio posible, dado lo anterior, los estudiantes deber´n
a a
conocer las propiedades que caracterizan a las unidades, cuales
son las magnitudes fundamentales en el Sistema Internacional de
Unidades y como se obtiene la unidad de una magnitud derivada
dada su definici´n.
o
Algunas medidas de uso com´n eran:
u
El Almud (mas conocido como almur).
La Vara.
La cuarta.
El geme.
El Kilo.
El litro.
La lata de sardina
etc.

59. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 47
Actividad. 1.2
1. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
2. En equipo dise˜e cinco preguntas adecuadas para saber so-
n
bre cada una de las medidas de uso com´n mencionadas
u
anteriormente. las preguntas deben ser del tipo:
a) Conoce o ha usted usado el . . .
b) Me podr´ usted decir que es, como es, o como hacer un
ıa
...
c) Conoce usted la equivalencia entre el . . . y el . . .
d) . . . . . .
3. Aplique la encuesta a diez personas de edad mayor (padres,
abuelos, conocidos) sobre: las medidas de uso com´n.
u
4. Con base en las respuestas obtenidas, escriba las definicio-
nes de cada una de las medidas de uso com´n mencionadas
u
anteriormente y algunas equivalencias que se conozcan entre
ellas.
5. para la evaluaci´n se tomar´ en cuenta:
o a
a) Entrega en tiempo y forma (dos semanas m´ximo).
a
b) Claridad en las definiciones presentadas.
c) Coherencia de lo escrito.
d) Validez y pertinencia de las ideas expuestas (que tenga
relaci´n con la situaci´n actual).
o o
e) Presentaci´n.
o
f ) Profundidad de las definiciones.
g) N´mero de equivalencias obtenidas.
u
6. Escriba en los espacios correspondientes de este libro, las
definiciones mas adecuadas para las medidas de uso com´n u
y las equivalencias encontradas.

60. 48 Introducci´n al Conocimiento de la F´
o ısica
1.2.1. Magnitudes Fundamentales y Derivadas.
La observaci´n de un fen´meno es en general incompleta a
o o
menos que d´ lugar a una informaci´n cuantitativa. Para obte-
e o
ner dicha informaci´n se requiere la medici´n de una propiedad
o o
f´
ısica. As´ la medici´n constituye una buena parte de la rutina
ı, o
diaria del ser humano.
La medici´n es la t´cnica por medio de la cual
o e
se asigna un n´mero a una propiedad f´
u ısica.
Medir: Es el resultado de la comparaci´n de una
o
propiedad con otra similar tomada como patr´n, la
o
cual se ha adoptado como unidad.
Es decir que Medir es comparar las dimensiones de un cuerpo
con las de otro.
Las dimensiones del cuerpo contra el que se compara se llama
patr´n de medida o unidad de medida, sin embargo al medir un
o
cuerpo se tienen errores los cuales no se pueden eliminar pues
tienen diferentes causas por lo que ninguna persona o instru-
mento har´ medidas iguales.
a
Existen magnitudes de dos tipos: Fundamentales, las cuales
se definen y a partir de estas se obtienen las derivadas.

61. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 49
Magnitudes Fundamentales.
Las Magnitudes o Cantidades Fundamen-
tales son las unidades que se definen como base
para medir los diferentes cuerpos.
Generalmente se definen tres magnitudes o cantidades funda-
mentales:
La unidad de Masa.
La unidad de Longitud.
La unidad de Tiempo.
Magnitudes derivadas.
Cuando se realizan operaciones como sumar, multiplicar, di-
vidir, etc. estas operaciones tambien las experimentan las uni-
dades de medida, por ejemplo si se requiere sumar 3 metros con
4 metros, la operaci´n que se realiza es:
o
3m + 4m = 7m
es decir que el resultado conserva las unidades caracter´
ısticas de
las cantidades que sufrieron la operaci´n.
o
Otro caso es cuando se multiplica. Por ejemplo: 3kg con 4m
(3kg)(4m) = (3)(4)(kg)(m) = 12kgm
las unidades tambi´n se multiplicaron.
e

62. 50 Introducci´n al Conocimiento de la F´
o ısica
Las unidades de las Cantidades Derivadas se ob-
tienen al realizar operaciones entre unidades, asi se
obtienen otras unidades de medida.
A estas cantidades asi obtenidas se les conoce como Can-
tidades Derivadas ya que se obtienen como resultado de la
multiplicaci´n o divisi´n entre otras cantidades fundamentales.
o o
1.2.2. Sistemas de Unidades CGS e Ingl´s.
e
Un Sistema de Unidades es aquel al que se le de-
finen sus unidades primordiales de medida y luego
se utilizan para medir.
Sistema CGS.
Por ejemplo se puede medir las longitudes en cent´ ımetros
(cm), las masas en gramos (g) y el tiempo en segundos (s).
Cuando se toman estas tres unidades como fundamentales,
el sistema de unidades se llama Sistema de Unidades CGS,
siendo las iniciales las de las unidades fundamentales.
Con estas tres unidades fundamentales, se pueden obtener to-
das las otras unidades derivando las dem´s unidades de medida
a
al realizar operaciones entre estas unidades fundamentales.

63. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 51
Sistema Ingl´s de Unidades.
e
Asi tmbi´n en E. U. e Inglaterra, las unidades que se toman
e
como fundamentales son: para la masa la libra masa (lb), para
la longitud el pie (ft) y para la fuerza la libra fuerza (pd), es
decir que ahi las cantidades fundamentales son cuatro y no tres
como para el sistema CGS.
1.2.3. El Sistema Internacional de Unidades, Ventajas
y Limitaciones.
Por legislaci´n, en M´xico se utiliza el Sistema Internacional
o e
de Unidades (S I) el cual tiene las siguientes unidades patr´n:
o
Unidad de Masa. Cantidad de materia que contiene un cuerpo.
En el Sistema Internacional de Unidades (SI), se define como:
La Masa de un cilindro de Platino e Iridio que
se conserva en la oficina internacional de pesas y
medidas en S`vres Francia.
e
Su unidad de medida es el kilogramo[kg].
Unidad de Longitud. Es el metro [m],
1
es la longitud que recorre la luz en 299,792,458 s
ex´ctamente..
a

64. 52 Introducci´n al Conocimiento de la F´
o ısica
Unidad de tiempo: En el S I es el segundo:
Es la duraci´n de 9, 192, 631, 770 ciclos de la
o
radiaci´n correspondiente a la transici´n entre los
o o
dos niveles hiperfinos del estado fundamental del
´tomo de Cesio 133 (133 Cs)
a
SI abr. CGS abr. ´
INGLES abr.
LONGITUD metro (m) cent´
ımetro (cm) pie (f t)
MASA kilogramo (kg) gramo (g) libra (pd)
TIEMPO segundo (s) segundo (s) segundo (s)
Cuadro 1.5: Unidades Fundamentales en tres Sistemas de Unidades.

65. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 53
Ventajas y Limitaciones del S. I. U.
El SI, naci´ como un deseo de uni-
o
ficar todos los sistemas de unidades co-
nocidos, todo esto como una consecuen-
cia de la Revoluci´n Francesa que en la
o
epoca de Napole´n, bajo la coordinaci´n
o o
de Joseph Louis Lagrange, se realiz´ es-
o
te intento mediante la realizaci´n de un
o
congreso internacional que se llev´ a ca-
o
bo en S`vres Francia, al cual por cierto,
e
nuestro pais envi´ como delegado a un
o
poeta, sin embargo, los paises anglosajo-
nes, aunque asistieron, por la rivalidad
cient´ıfica con Francia decidieron no aca-
tar los acuerdos y tal unificaci´n no se
o
llev´ a cabo.
o
La ventaja de tener un solo sistema de medici´n es eviden-
o
te, pues la ciencia el comercio y la legislaci´n solo tendr´ que
o ıa
utilizar este sistema para la medici´n en todo el planeta.
o
En la pr´ctica esto no result´ tan sencillo, por esto, se dan
a o
aqu´ algunos ejemplos que constituyen las deventajas del SI.
ı
En lo muy peque˜o, lo ideal ser´ que el patr´n de masa
n ıa o
fuera la masa del electr´n, sin embargo es muy peque˜a
o n
−31
(9,11 × 10 kg) dando como resultado que las dem´s me-
a
didas ser´ muy grandes, por lo que se utiliza actualmente
ıan
el mol.
En 1790, en la conferencia de S`vres, se defini´ el metro
e o
como la cuarentamillon´sima parte del meridiano terrestre
e
que pasa por S`vres, con el tiempo mediciones mas exactas
e

66. 54 Introducci´n al Conocimiento de la F´
o ısica
demostraron que por la rotaci´n de la tierra el meridiano se
o
ensancha, por lo que result´ ser de 40009.153 m. La defini-
o
ci´n de metro tuvo que modificarse sucesivamente, en 1875,
o
1959, 1960 y finalmente en 1983 donde quedo como se dijo
en el p´rrafo 1.2.3.
a
La unidad de tiempo es el segundo, inicialmente se defi-
ni´ en funci´n del a˜o solar medio de 1900, esta definici´n
o o n o
tambi´n tuvo que ser modificada porque la rotaci´n de la
e o
tierra es variable con el tiempo, quedando en 1967 como se
defini´ en 1.2.3.
o
Unidades B´sicas del SI
a
En la XIV Conferencia General de pesas y Medidas de 1971 se
seleccionaron las unidades que constituyen la base del Sistema
Internacional de Unidades, las cuales se presentan en la tabla
1.6
CANTIDAD FUNDAMENTAL UNIDAD S´
IMBOLO
longitud metro m
Masa kilogramo kg
Tiempo segundo s
Corriente El´ctrica
e ampere A
Temperatura Termodin´mica
a kelvin K
Cantidad de Sustancia mol mol
Intensidad Luminosa candela cd
Cuadro 1.6: Unidades Fundamentales del SI.

67. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 55
Actividad. 1.2.3
1. Realice una investigaci´n sobre: La definici´n de las Unida-
o o
des Fundamentales del SI.
2. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
3. Con base en la investigaci´n realizada escriba La definici´n
o o
de las Unidades Fundamentales del SI.
4. Para la evaluaci´n de la actividad se tomar´ en cuenta:
o a
a) Entrega en tiempo y forma (una semana m´ximo).
a
b) Claridad.
c) Coherencia.
d) Validez y pertinencia de las ideas expuestas.
e) Profundidad de los conceptos.
f) Presentaci´n.
o
g) Profundidad del escrito.
5. Escriba en los espacios adecuados de este libro, las defini-
ciones que resulten mas adecuadas Unidades Fundamentales
del SI.
UNIDAD SI CGS ´
INGLES
1 metro 1 m 100 cm 3,2808 pie(ft)
1 kilogramo 1 kg 1000 g 2,2075 lb(pd)
1 segundo 1 s 1 s 1 s
Cuadro 1.7: Equivalencia entre Sistemas de Unidades.

68. 56 Introducci´n al Conocimiento de la F´
o ısica
1.2.4. M´todos Directos e Indirectos de Medici´n.
e o
Medici´n Directa.
o
Se realizan cuando lo que se mide es comparable con el propio
instrumento de medida,
p. e. La medici´n de una hoja de cuaderno.
o
Medici´n Indirecta.
o
Se realizan cuando para medir es necesario valerse de otros
par´metros medibles. p. e.
a
Distancia entre la tierra y el sol.
El ´rea de un cuerpo.
a
El volumen de un cubo, etc.
1.2.5. Notaci´n en Base 10 (Prefijos).
o
Una vez establecida la unidad patr´n se acuerdan los subm´lti-
o u
plos y m´ltiplos, los cuales son cantidades menores y mayores
u
de la unidad en cuesti´n. Se emplea el sistema m´trico decimal
o e
el cual como va de diez en diez, significa que se van tomado su-
cesivamente porciones de unidad 10 veces mas chica en el caso
de los subm´ltiplos, o 10 veces mas grandes en el caso de los
u
m´ltiplos. Si se divide el metro en diez partes, cada parte se lla-
u
ma dec´ ımetro (simbolizado con dm), en consecuencia un metro
contendr´ diez dec´
a ımetros, lo cual en s´
ımbolos se escribe: 1 m =
10 dm. Si el dec´ımetro se divide en diez partes, el metro queda
dividido diez veces en diez es decir que el metro se divide en
cien partes y cada parte se llama cent´ ımetro, un metro contiene
cien cent´ımetros es decir: 1m = 100cm. La mil´sima parte del
e
metro se denomina mil´ ımetro y entonces un metro contiene mil

69. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 57
mil´
ımetros o sea: 1m = 1000mm
1m = 10dm = 100cm = 1000mm
1m = 10dm = 102 cm = 103 mm
Esto conduce a los m´ltiplos de la unidad patr´n: diez metros
u o
corresponden a un dec´metro es decir 10m = 1Dm . Cien metros
a
corresponden a un hect´metro y mil metros a un kil´metro
o o
10m = 1Dm
100m = 1hm
1000m = 1km
Se utilizan prefijos para denotar las proporciones de subm´lti-
u
plos y m´ltiplos y estos prefijos se generalizan para cualquier
u
unidad. De ah´ que, por ejemplo, a la mil´sima parte del se-
ı e
gundo se la llame milisegundo, luego, un segundo contiene mil
milisegundos es decir:
1s = 1000ms
En un esfuerzo por eliminar la necesidad de arrastrar la ca-
dena de ceros asociada con los n´meros muy peque˜os o muy
u n
grandes, se defini´ la notaci´n cient´
o o ıfica (o compacta) que apa-
rece en la tabla 1.8.
Un conteo simple a partir del punto decimal hacia la dere-
cha del n´mero 1 da la potencia apropiada de 10 si se procede
u
de izquierda a derecha se obtiene un exponente negativo, y de
derecha a izquierda un exponente positivo.

70. 58 Introducci´n al Conocimiento de la F´
o ısica
N´ mero
u Not. Base 10 Nombre Abreviatura
1, 000, 000, 000, 000, 000, 000 1018 exa E
1, 000, 000, 000, 000, 000 1015 peta P
1, 000, 000, 000, 000 1012 tera T
1, 000, 000, 000 109 giga G
1, 000, 000 106 mega M
1000 103 kilo k
100 102 Hecto H
10 101 Deca D
1 100 uno
1
10
10−1 deci d
1
100
10−2 centi c
1
1000
10−3 mili m
1
1000,000
10−6 micro µ
1
1000,000,000
10−9 nano n
1
1000,000,000,000
10−12 pico p
1
1000,000,000,000,000
10−15 femto f
1
1000,000,000,000,000,000
10−18 atto a
Cuadro 1.8: Potencias de Base 10

71. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 59
1.2.6. Transformaci´n de Unidades Entre Sistemas.
o
Cuando se habla de un microsegundo se refiere a una mi-
llon´sima de segundo es decir que 1 µs = 1×10−6 s = 0,000001s.
e
Cinco hectolitros se escribe 5 hl (l es la letra “ele”, abreviatura
de litro) que corresponde a 5 × 102 l.
Suponga que se quiere indicar el espesor de un alambre cuyo
di´metro es de 0,002 m, “cero punto, cero, cero, dos metros”
a
¿no es mas sencillo decir 2 mm o sea “dos mil´ ımetros”? Se co-
noce la distancia aproximada de D. F. a Veracruz la cual es
de aproximadamente 400 km, pero no es com´n escuchar esa
u
distancia expresada en metros.
Ahora ¿ha escuchado expresar cantidades de magnitud en
unidades diferentes a las cuales se acostumbra, como por ejem-
plo:
100 millas; 5 yardas; 120 Fahrenheit; 3 pulgadas; 8 onzas; 20
nudos, etc.?
Aqu´ se utiliza el sistema internacional de unidades pero a´n
ı u
hay naciones que emplean, sistemas basados en otros patrones
de medida, en consecuencia se tiene que encontrar el modo de
transformar esas unidades a las del SI para poder saber de que
medida se est´ hablando.
a
La manera de transformar es a trav´s de las equivalencias de
e
unidades. Por ejemplo en el sistema de medida ingl´s la unidad
e
es la pulgada, cantidad de longitud que corresponde a 0.0254 m
o 2.54 cm o 25.4 mm etc. En otro ejemplo una onza equivale a
28.34 gramo, adem´s este sistema no tiene m´ltiplos decimales:
a u
en el caso de la longitud , un m´ltiplo inmediato de la pulgada es
u
el “pie” que corresponde a 12 pulgadas, despu´s sigue la yarda
e
que corresponde a 3 pies, etc. como se ve la proporci´n no va de
o
diez en diez. En el caso de la onza, un m´ltiplo inmediato es la
u

72. 60 Introducci´n al Conocimiento de la F´
o ısica
libra que corresponde a 16 onzas
1pulgada = 2, 54cm
1onza = 28, 34g
1pie = 12pulgadas
1yarda = 3pies
1libra = 16onzas
Una transformaci´n de unidades consiste en ex-
o
presar una cierta magnitud que est´ dada en una
a
cierta unidad, en otra ya sea del mismo sistema de
medida o en otro.
Para ello es necesario conocer las equivalencias entre las uni-
dades en cuesti´n.
o
Por ejemplo; sea una cierta cantidad de longitud, por ejemplo
58 cm y se desea:
a) Expresarla en metros
b) Expresarla en pulgadas
a) Se sabe que 1m = 100cm, Si se pasa los 100 cm dividiendo
al primer miembro, nos queda
1m
=1 (1.2)
100cm
ahora escribiendo
(58cm) (1) = 58cm

73. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 61
es decir que no se alter´ el resultado, pero de (1.2) 1 =
o
1m
100cm , entonces
1m 58cm 1m
(58cm) =
100cm 1 100cm
Multiplicando numeradores y denominadores se tiene:
58cm m
ւ
(58cm) =
100cm
ւ
58m
= 0,58m
100
(58cm) = 0,58m
muchos dir´n que es mas f´cil correr el punto y ya, sin
a a
embargo se ver´ que es el unico modo de convertir unidades
a ´
mas complejas y que una vez que se aprende el mecanismo,
notar´n que es sencillo ya que consiste en un despeje, una
a
sustituci´n y una operaci´n final.
o o
b) Ahora 1pulgada = 2,54cm, Si se pasa los 2,54 cm dividiendo
al primer miembro, nos queda
1pulgada
=1 (1.3)
2,54cm
nuevamente escribiendo
(58cm) (1) = 58cm
1pulgada
de (1.3) 1 = 2,54cm , entonces
1pulgada 58cm 1pulgada
(58cm) =
2,54cm 1 2,54cm

74. 62 Introducci´n al Conocimiento de la F´
o ısica
Multiplicando numeradores y denominadores se tiene:
58cm pulgada
ւ
(58cm) =
2,54cm
ւ
58pulgada
= 22,83pulgada
2,54
⇒ (58cm) = 22,83pulgada
Mas ejemplos . . .
Se sabe que una hora contiene 60 minutos, a su vez un minuto
contiene 60 segundos, por lo que se puede afirmar que 1 h con-
tiene 60 veces 60 s , es decir 60 × 60 segundos lo que da un total
de 3600 s . Luego se puede escribir las siguientes equivalencias:
1h = 60min
1min = 60s
1h = 3600s
Se desea saber cuantos minutos corresponden a 18 s
Soluci´n
o
1) Se busca la relaci´n entre segundos y minutos
o
1min = 60s
2) como se quiere pasar de segundos a minutos despejando de
nuestra relaci´n de equivalencia pasando el 60 s dividiendo
o
queda:
1min
=1
60s
3)
18s 1min 18s min
ւ
=
1 60s 60s
ւ
⇒ 18s = 0,3min

75. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 63
Unidades Derivadas Por ejemplo la velocidad se expresa en m os
N
el peso espec´
ıfico que se expresa en m3 , etc. en estos casos resulta
mas dif´ realizar la conversi´n de unidades a subm´ltiplos o
ıcil o u
m´ltiplos de las mismas o a otro sistema de unidades, por esto
u
se justifica aplicar el siguiente procedimiento:
Procedimiento 1.2.6
Paso 1. Iniciar poniendo la cantidad a convertir, como
un cociente explicito.
Paso 2. Multiplicar por una equivalencia en forma de
cociente, de manera que al multiplicarse, las
unidades en el numerador puedan dividirse y
convertirse en la unidad (comunmente se cono-
ce como eliminaci´n de unidades).
o
Paso 3. Repetir el paso 2 hasta obtener las unidades
deseadas.
Es necesario anotar que cuando las unidades est´n
a
elevadas al cuadrado o cubo, el cociente debe tam-
bi´n elevarse a la potencia requerida.
e
Ejemplo: 1.2.6.1
m km
Expresar una velocidad de 5 s en hr
Paso 1 Paso 2 paso 3
5m 1km 3600s
· ·
1s 1000m 1hr

76. 64 Introducci´n al Conocimiento de la F´
o ısica
Multiplicando los numeradores y denominadores (culmina-
ci´n del Paso 2):
o
18000m kms
ւ ր km
= 18
1000s m hr
ր ւ hr
Ejemplo: 1.2.6.2
Una unidad astron´mica (UA) es la distancia promedio de
o
la tierra al Sol, que aproximadamente es de 1.5×108 km.
(150,000,000 km), La rapidez de la luz (c) es de alrededor
de 3,0 × 108 m . Expresar la velocidad de la luz en t´rminos
s e
de unidades astron´micas por minuto.
o
Soluci´n:
o
Si una U A = 1,5 × 108 km y c = 3,0 × 108 m ,
s
entonces la rapidez es;
m
3,0×108 ր 60s
ր 1km
ւ UA UA
c= 1
s
min 103 m 1,5×108 km
ւ = 0.12 min
UA
⇒ c =0.12 min
la distancia es:
1,5 × 108 km
ւ 103 m
= 1,5 × 1011 m
1 1km
ւ
Ejemplo: 1.2.6.3
masa
Suponer que la densidad (̺ = volumen ) del agua es exactamente
g
1 cm3 , expresar la densidad del agua en kilogramos por metro
kg
c´bico ( m3 )
u

77. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 65
Soluci´n:
o
Ya que 1kg = 1 × 103 g, entonces;
ւ
g 1kg 106 cm3
ր kg
1 = 103
cm3
ր 1 × 103ւ
g 1m3 m3
Suponer que un recipiente con 5700m3 de agua toma 10h pa-
ra drenarse ¿Cu´l es el flujo de masa en kilogramos por
a
segundo de agua del recipiente?
Soluci´n:
o
Puesto que 1m3 = 1000kg entonces;
5,700m3
ւ kg 1hr
ր kg
1000 = 158,3
10hr
ր m3
ւ 3600s s
Ejercicios
kg
1. Expresar 8000 m3 en:
kg
a) dm3
kg
Soluci´n: 8
o dm3
g
b) cm3
g
R: 8 cm3
2. Expresar 90 km en:
hr
m
a) s

78. 66 Introducci´n al Conocimiento de la F´
o ısica
m
R: 25 s
cm
b) s
cm
R: 2500 s
cm
c) min
cm
R: 150000 min
3. Expresar 2,5 gcal en
◦C
J
kg ◦ C ; (1J = 0,24 cal )
R: 10416,67 kgJ C
◦
1.2.7. 1a Autoevaluaci´n
o
Nombre del alumno ————————————– Gpo. 30———-
I.- Subraya la Respuesta Correcta a las Siguientes Preguntas
1.1 GENERALIDADES
1. Que es la ciencia?
a) el que dise˜a b) se encarga
n c) conjunto de
herramientas del estudio de conocimientos
y maquinas materia y energ´ Sistematizados.
ıa.
2. Qu´ es la tecnologia?
e
a) m´todos para
e b) se encarga c) conjunto de
resolver problemas del estudio de conocimientos
practicos materia y energ´ Sistematizados.
ıa.

79. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 67
3. Qu´ es la f´
e ısica?
a) m´todos para
e b) ciencia de c) encarga del
resolver problemas los oficios. estudio de la
pr´cticos.
a materia y energ´
ıa.
4. Con que otro nombre se le conoce a la tecnolog´
ıa?
a)El estudio b) el conocimiento c) comprensi´n
o
o la ciencia de de los m´todos.
e del entorno
los oficios. material.
5. Cu´l es la parte mas importante de la ciencia?
a
a) C´mulo de b) aplicaci´n
u o c) proyecci´n.
o
conocimientos. de los m´todos.
e
6. cuales son los resultados que dan como union la ciencia y
la tecnolog´
ıa?
Beneficios b) comprensi´n c) creaci´n de
o o
hacia la del entorno conocimientos
sociedad. Material.
7. Cu´les son los procesos que se aplican al descubrimiento de
a
la tecnolog´
ıa?
Beneficios b) comprensi´n c) creaci´n de
o o
hacia la del entorno conocimientos
sociedad. Material.
8. Fue un gran pionero de la f´
ısica proporciono los fundamen-
tos de la hidrost´tica
a
a) Arqu´
ımedes b) Einstein c) Newton

80. 68 Introducci´n al Conocimiento de la F´
o ısica
9. Postula que la sustancia b´sica es el agua
a
a) Thales de Mileto b) Arist´teles c) S´neca
o e
10. Descibe una cosmolog´ directa)
ıa
a) Copernico b) Aristarcos c) Pit´goras
a
11. Desarrollo la teor´ del universo
ıa
a) Dem´crito b) Anax´goras c) Emp´docles
o a e
12. Es considerado como el padre de la F´
ısica Moderna
a) Michael fadaray b) Tycho brahe c) Galileo Galelei
13. Creo el motor el´ctrico
e
A) Michael Faraday b) Aristarchus c) Newton
14. Desarrollo la teor´ ondulatoria de la luz y describi´ la in-
ıa o
terferencia de la luz
A) Kepler b) Thomas Young c) Democrito
15. Desarrollo la leyes de la mec´nica
a
A) Isaac Newton b) Aristarchus c) Tycho Brahe
16. Explico la curvatura del tiempo
a) Marie Curie b) Hamilton c) Einstein
17. En que a˜o se descubre la part´
n ıcula delta
a) 1872 b) 1949 c) 1875

81. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 69
1.1.1 LA F´
ISICA Y SU IMPACTO EN LA CIENCIA Y LA TEC-
NOLOG´ IA
1. Responde a preguntas mas que nada te´ricas
o
a) Ciencia b) Matem´ticas c) F´
a ısica
2. Son generalmente m´todos para resolver problemas pr´cti-
e a
cos
a) Tecnolog´ b) ciencia c) M´todo Cient´
ıa e ıfico
3. Son el resultado de beneficios para las sociedades es decir
se dise˜a, proyecta y se crea
n
a) Ciencia y Tecnolog´ b) Ciencias Naturales c) Tecnolog´
ıa ıa
y Rob´tica
o
4. Son conjuntos de conocimientos ordenados y jeraquizados
a) Matem´ticas b) Ciencia c) Tecnolog´
a ıa
5. Esta nos ayuda a tener un mejor estado social
a) Geograf´ b) Rob´tica c) Tecnolog´
ıa o ıa
6. Ellos hacen la ciencia
a) Doctores y Maestros b) Profesores c) Humanidad
7. Es un ejemplo de tecnolog´
ıa
a) Rob´tica b) Conocimiento Matem´tico c) Filosof´
o a ıa
8. Es una creaci´n innovadora del hombre
o
a) carros b) sillas c) mesa
9. Esta se crea
a) Materia b) Tecnolog´ c) Aritm´tica
ıa e

82. 70 Introducci´n al Conocimiento de la F´
o ısica
10. Es todo aquello que ocupa un lugar en el espacio
a) Masa b) Materia c) Hidrost´tica
a
1.1.2 Los M´todos de Investigaci´n y su Relevancia en el Desarrollo
e o
de la Ciencia
1. Es un m´todo indispensable para la ciencia
e
a) M´todo Cient´
e ıfico b) M´todo Matem´tico c) M´todo
e a e
Qu´ımico
2. En este paso se investiga preliminarmente al fen´meno
o
a) Ciencia b) Observaci´n c) Hip´tesis
o o
3. Repetici´n del fen´meno cuantas veces sea necesario
o o
a) Ciencia b) experimentaci´n c) Conclusi´n
o o
4. Constata los resultados
a) Experimentaci´n b) Hip´tesis c) Planteamiento
o o
5. Si se cumple la: hip´tesis se enuncia una
o
a) teor´ b) experimentaci´n c) Ley
ıa o
6. Es un conjunto de leyes
a) Teor´ b)Mapa c)Ley
ıa
7. Son resultados que explican el fen´meno
o
a) Hip´tesis b) Ley c) Ciencia
o
8. En este se observa como sucede el fen´meno
o
a) Observaci´n b) Proceso c) Funciona
o

83. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 71
9. M´todo experimental
e
a) Ciencia b) M´todo Cient´
e ıfico c)Historia
10. Ciencia que estudia la estructura y la interacci´n de la ma-
o
teria
a) Qu´
ımica. b) Matem´ticas c)F´
a ısica
1.2 Magnitudes F´
ısicas y su Medici´n
o
1. Se creo durante la Revoluci´n Francesa
o
A) SI B) CGS C) cm, m, km d) Sistema M´trico Decimal
e
2. Son las principales unidades de medida del SI
a) Metro, kilogramo y segundo b) longitud, masa y tiempo
c)metro, segundo y kilogramo
3. Significa Sistema Internacional de Unidades
a) SIU B) SI C)CGS
4. Es la t´cnica por la cual se asigna el n´mero de medida
e u
a) Medici´n b) Peso c) Tiempo
o
5. Es el resultado de la comparaci´n de un cuerpo con otro
o
a) medir b)peso c)kilogramo
6. Son las magnitudes Fundamentales
a) Longitud masa y tiempo b) kilogramo s, km c) m, kg,
Segundo,

84. 72 Introducci´n al Conocimiento de la F´
o ısica
7. Son las cantidades derivadas
a) Se obtienen a trav´s de divisi´n multiplicaci´n, etc. b)
e o o
Son lo mismo que las fundamentales c) se inventan
8. Esta es una unidad fundamental
a) Masa b)metro c)tiempo
9. Se caracteriza por la unidad de medida llamada metro
a) Longitud b) Masa C) kilogramo
10. Se obtienen de las medidas fundamentales
a) Diversas b) Derivadas c) Fundamentales
1.2.1 Magnitudes Fundamentales y Derivadas
1. Se utilizan para, medir diferentes cuerpos
a) Magnitudes Fundamentales b) Cuerpos c) Cilindros
2. Se obtienen como resultado de la multiplicaci´n o divisi´n
o o
de unidades.
a) Derivadas b) Cuanti´ c) Fundam´ntales
ıtas e
3. Existen dos tipos
a) Fundamentales y derivadas b) Cuanti´ c) Matem´ticas
ıta a
4. Es comparar las dimenciones con otro cuerpo
a) Medir b) Masa c) Tiempo

85. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 73
5. las diemsiones del cuerpo contra el que se compara se le
llama
a) Patr´n b) Medida c) Formato
o
1.2.2 Sistemas De Unidades CGS e Ingl´s
e
1. Es aquel que se define por sus unidades
a) Masa b) Sistema c) Mapa
2. Forman al Sistema CGS
a) ml y cm b) cm y kg c) cm g y s
3. Son las unidades fundamentales en Inglaterra
a) Masa, tiempo y segundo b) lb, y ft c) my s
4. Se define con las siglas CGS
A) cm, g y s b)t,g y m c)s,t y dm
5. Se obtienen de las fundamentales
a) Masa b) Tiempo c) Derivada
6. Que une al macromundo
a) conforma la tierra. b) Protones y neutrones c) Esta unido
por la fuerza Del n´cleo. Gravitacional.
u
7. Que significa micromundo
a) Propiedades muy peque˜as b) Fen´menos F´
n o ısicos que
presentan c) Constituye al universo Al nivel at´mico
o

86. 74 Introducci´n al Conocimiento de la F´
o ısica
8. Que significa volumen
a) Es aquel que se mide b) Espacio que ocupa un cuerpo
c) Cantidad de materia que contiene En cent´
ımetros. Un
cuerpo.
9. Que significa densidad
a) Cociente entre la masa y b) Fuerza de atracci´n que
o
ejerce c)Caracter´
ısticas de la materia
10. Menciona un ejemplo de fen´meno Biol´gico
o o
a) Crecimiento de un ´rbol b) Al llover b) al tirar alg´n
a u
objeto. El volumen de un cuerpo. La tierra sobre la materia.
1.2.3 El Sistema Internacional de Unidades, Ventajas y Limitacio-
nes
1. Este Sistema se Utiliza en M´xico
e
a) SI b) CGS C) ITC
2. Cantidad de materia que posee un cuerpo
a) Peso b) Unidad de masa c) Antimateria
3. Es la unidad que recorre la luz
a) Unidad de Longitud b) masa c) Luz
4. Es la duraci´n de ciclos en la radiaci´n
o o
a) Masa b) Unidad de tiempo c) peso
5. Naci´ como el deseo de unificar a todos los sistemas
o
a) SI b) tiempo c) Duraci´n
o

87. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 75
6. Que es f´
ısica
a) Ciencia que se encarga b)conjunto de conocimientos c)Todo
lo existente en la naturaleza Del estudio de la materia or-
denados
7. Que es ciencia
a) Conjunto de conocimientos b) Comprender y explicar
los c)Estudia a la naturaleza Ordenados y Jerarquizados.
Fen´menos
o
8. De cuantas divisiones consta la F´
ısica y cuales son
a) De 2 Cl´sica y moderna b) De 5 mec´nica, calor, sonido,
a a
c) 1 Cu´ntica. Luz, magnetismo.
a
9. Menciona un ejemplo de un fen´meno Qu´
o ımico
a) Al cortar un papel b) Al quemar un papel c) Al vaciar
agua a un recipiente.
10. Menciona cuatro tipos de fuerzas
a) Gravitacional, el´ctrica, nuclear b) Natural, f´
e ısica, qu´
ımi-
ca, universal. c) A´rea, territorial, acu´tica, y d´bil. Biol´gi-
e a e o
ca.
1.2.4 M´todos Directos e Indirectos de Medici´n
e o
1. Qu´ es una medida directa
e
a) Cuando lo que se mide es b )Lo que se mide c)Son me-
didas Comparable con el mismo instrumento

88. 76 Introducci´n al Conocimiento de la F´
o ısica
2. Es un ejemplo de medida directa
a) Masa b) La medici´n de una hoja de cuaderno c) La
o
masa ye l tiempo
3. Es comparable con su propio instrumento
a) Masa b)cuerpo c)Medida directa
4. Son dos tipos de m´todos
e
a) Base y metro b) Longitud y distancia c) Directos e indi-
rectos
5. Necesitan de otro patr´n para ser medidas
o
a) Mediadas indirectas b) Medidas indirectas c) Volumen
6. Se realizan para cuando para medir se necesitan de otro
par´metro
a
a) Medidas directas indirectas b) Medidas indirectas c) No-
taci´n de base
o
7. El ´rea de un cuerpo es ejemplo de
a
a) Medida directa b) Medida indirecta c) Densidad
8. La Distancia entre el sol y la tierra es ejemplo de
a) Medida b) Distancia c ) Medida indirecta
9. En que se diferencia la medida ¡directa de la indirecta
a) Que se mide con su propio patr´n y necesita de otro para
o
se¡medida b) Son iguales c)Es lo mismo
10. El volumen de un cubo es ejemplo de
a) Medida indirecta b)Medida directa c)Medida directa e
indirecta

89. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 77
1.2.5 Notaci´n Cient´
o ıfica y Prefijos
1. Son cantidades menores y mayores de¡la unidad en cuesti´n
o
a) Prefijos de 10 b) Subm´ltiplos y m´ltiplos c) Notaci´n
u u o
cient´
ıfica
2. Cu´ntos cm tiene un metro
a
a) 10 dm b) 0.0100cm c) 0100cm
3. C´mo se le denomina a la mil´sima parte metro
o e
a) Cent´
ımetro b) Millon´sima c) Mil´sima
e e
4. A cuantos metros equivale un dec´metro
a
a)10 m b)20 m c)100m
5. Se utilizan para denotar las proporciones de subm´ltiplos
u
y m´ltiplos
u
a) Prefijos b) Bases c) T´rminos
e
6. Cu´nto tiempo contiene un segundo
a
a) 60 s b) 100ms c) 300m
7. Es el nombre de algunos prefijos en base 10
a) Penta y cent´
ıgrado b) exa, peta y tera c)ms, masa y
tiempo
8. Es el valor de exa
a)1018 b) 106 c) 1012
9. Es la representaci´n del prefijo mega
o
a) Mega b) m c) M

90. 78 Introducci´n al Conocimiento de la F´
o ısica
10. Es el valor del prefijo mega
a) 108 b) 106 c) 109
1.2.6 Transformaci´n de Unidades de un Sistema a Otro
o
1. Cu´ndo se habla del micro mundo se refiere a
a
a) Una millon´sima b) Toneladas c) Montones
e
2. Cu´ntos tipos de Sistemas hay
a
a) CGS Y SIU b) TCI Y GFT C) CGS Y ST
3. Es una equivalencia de unidades de peso
a) Masa b) Tiempo c) libra fuerza
4. A cuanto equivale una pulgada en cm
a) 2,5 cm b) 2.2cm c) 2,54 cm
5. Consiste en expresar cierta magnitud que esta dada en cier-
ta unidad
a) Transformaci´n de unidades b) Masa c) Tiempo
o
6. Es el Sistema que se utiliza en todo el mundo
a) CJT b) FGT C) SIU
7. Cuanto equivale un metro en cm
a) 100ml b) 100 cm c) 1000ml
8. A cuantos minutos Equivale una hora
a) 80 min. b) 60 fines c) 60 min.

91. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 79
9. A cuanto equivale un dec´
ımetro en cm
a) 10 cm b)3 ton 4) mil´
ımetros
10. A cuanto equivale una hora en segundos
a) 800s b) 3600s c) 8400s
1a Autoevaluaci´n (continuaci´n)
o o
Nombre del alumno —————————————— Gpo. 30 ———-
I.- Escribe dentro del Par´ntesis la letra que corresponda.
e
1.- ¿Cual de los siguientes enunciados es una hip´tesis cient´
o ıfica? ( )
a) Los ´tomos son las part´
a ıculas de materia mas
peque˜as que existen
n
b) El universo est´ rodeado de otro universo el cual
a
no se detecta de ninguna manera
c) Alberto Einstein es el fisico mas grande del siglo XX
2.- Cual de las disciplinas siguientes implican grandes cantidades de ( )
pasi´n talento e inteligencia humana
o
a) Arte b) Literatura c) M´sica d) Ciencia e) Todas las anteriores
u
3.- El submultiplo llamado micro segundo se escribe: ( )
1 1
a) 100 m b) µ s c) 1000 s d) mm
4.- De los sistemas de medici´n siguientes cuales son actuales
o ( )
a) Mks, CGS y SI b) Ingl´s, Cgs y Mks c) SI, Ingl´s y CGS d) a y c
e e
5.- La F´ ısica es: ( )
a) La ciencia mas fundamental b) mejor que la literatura
c) Igual que la Qu´ımica
II.- Completa cada una de las siguientes definiciones.
1. El lenguaje cuantitativo de la f´
ısica es la: ——————–
2. La finalidad de la ciencia es crear: —————————-
3. La longitud, la masa y el tiempo son las cantidades: ————————–
4. El peso es una cantidad: ———————————–
5. Para obtener la densidad la masa y el volumen se: —————————–
III Problemas

92. 80 Introducci´n al Conocimiento de la F´
o ısica
1. Exprese con los multiplos y submultiplos de 10, (pueden resultar palabras
no ortogr´ficas):
a
a). 101 idos
b). 10−1 didos
c). 10−2 mientos
d). 10−18 micos
e). 10−12 tazos
2. Cual el n´mero de km equivalentes a 20 millas, si se sabe que : 1milla =
u
5280f t, 1f t = 12pulg.

93. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 81
Para evitar la incidencia de errores en la medici´n, el tipo de
o
errores y su tratamiento estad´ıstico se estudia en la teor´ de la
ıa
medici´n.
o
1.2.8. La Precisi´n de los Instrumentos de Medici´n,
o o
Tipos de Errores.
Error en la medida:
En una cantidad, es la diferencia entre el valor verdadero,
suponiendo que se conoce y una aproximaci´n al valor verdadero,
o
o la cantidad en que el valor obtenido en un c´lculo o en una
a
medici´n difiere del valor exacto.
o
Ea = Vv − Vc (1.4)
Ea = Error absoluto
Vv = Valor verdadero
Vc = Valor medido o calculado.
• Tipos de Error.
Sistem´tico: Se clasifican en cuatro clases: instrumentales,
a
te´ricos, ambientales y sistem´ticos. Estos se deben a cau-
o a
sas identificables.
Aleatorios: Se deben a variables no controladas.
Por defecto: Debido a equipos descalibrados o en mal esta-
do.
Observacionales: De paralaje dependen de la posici´n desde
o
donde se observe la escala de medici´n.
o
Calibraci´n: Es instrumental es un error del instrumento.
o

94. 82 Introducci´n al Conocimiento de la F´
o ısica
Escala: Es tambi´n un error instrumental.
e
Ambientales: se deben a cambios impredecibles. Por ejem-
plo variaciones de la presi´n, temperatura, la humedad, el
o
ruido electr´nico y otros factores.
o
Te´ricos: Se deben a la simplificaci´n de las teor´
o o ıas.
Errores Aleatorios, estoc´sticos o circunstanciales: Se deben
a
a variables no controladas que inciden en la estad´
ıstica, sus
causas son Observacionales y ambientales.
Observacionales: Son debidos al juicio o la reacci´n del ob-
o
servador.
Error relativo:
Es el cociente entre el error absoluto y la aproximaci´n;
o
Ea Vv − Vc
Er = = ¯ (1.5)
aprox V
El error relativo se da frecuentemente en porcentaje ( %), por lo
que se hace:
Ea
Er = × 100
aprox
n
¯ i=1 Vi
aproximaci´n = V = V =
o (1.6)
n
V1 + V2 + V3 + ...Vn
V =
n
la aproximaci´n es la suma de todos los valores medidos, divi-
o
dida por el n´mero de valores. Esta cantidad se le conoce como
u
el valor promedio, “aproximaci´n”,“valor verdadero” o “valor
o
medio”

95. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 83
Ejemplo: 1.2.8.
Se ha medido el tiempo (t) cuatro veces los resultados han
sido: 6.3 s, 6.2 s, 6.4 s y 6.2 s
Encuentre:
a). El Valor promedio (valor verdadero o aproximaci´n).
o
¯ 6,3 + 6,2 + 6,4 + 6,2
aprox = V = V =
4
¯ 25,1
V = = 6,275 ≈ 6,3
4
b). El error absoluto para cada medida.
Ea = V − Vc
Ea1 = 6,3 − 6,3 = 0,0
Ea2 = 6,3 − 6,2 = 0,1
Ea3 = 6,3 − 6,4 = −0,1
Ea4 = 6,3 − 6,2 = 0,1
c). El error relativo para cada medici´n.
o
Ea
Er =
aprox
Ea1 0
Er1 = =
V 6,3
Er1 = 0,0
Ea2 0,1
Er2 = =
V 6,3
Er2 = 0,0158

96. 84 Introducci´n al Conocimiento de la F´
o ısica
−0,1
Er3 =
6,3
Er3 = −0,0158
0,1
Er4 =
6,3
Er4 = 0,0158
d). El Error relativo en %
0,0
Er1 = × 100
6,3
Er3 = 0 %
0,1
Er2 = × 100
6,3
Er2 = 1,58 %
Er3 = − 0,0158 × 100 = −1,58 %
Er4 = 0,0158 × 100 = 1,58 %
e). El promedio del error absoluto.
Ea1 + Ea2 + Ea3 + Ea4
Ea =
4
0 + 0,1 + (−0,1) + (0,1)
Ea =
4
0,1
Ea =
4
Ea = 0,025

97. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 85
Figura 1.10: Mapa Conceptual de Los Diferentes Tipos de Errores.

98. 86 Introducci´n al Conocimiento de la F´
o ısica
Reglas Para Expresar Medidas y Su Error.
1. Todo resultado experimental debe ir acompa˜ado del valor
n
promedio del error absoluto y enseguida sus unidades de
medida.
X = 297 ± 2mm
Limsup = 299mm
Liminf = 295mm
2. Los errores se deben dar con una cifra significativa sola-
mente.
297 ± 2mm correcto
245 ± 2,98mm incorrecto
245 ± 3m correcto
3. La ultima cifra en el valor de la magnitud y su error deben
´
corresponder al mismo orden de magnitud
24000 ± 3000m
Limsup = 27000m
Liminf = 21000m
24,00 ± 0,06
Limsup = 24,06
Liminf = 23,94

99. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 87
Ejercicio 1.2.8. Se ha medido el tiempo (t) para un experimento
los resultados han sido: 5.5 s, 5.7 s, 6.2 s y 6.5 s
Encuentre:
a). El Valor promedio (valor verdadero o aproximaci´n).
o
b). El error total.
c). El valor absoluto del error total.
d). El error relativo para cada medici´n.
o
e). El Error cuadr´tico.
a
f ). Exprese cada medici´n en corcondancia con las reglas para
o
expresar la medida y su error.
Nota: si en este ejercicio existe alg´n concepto que usted no
u
conoce, debe aplicar lo que ha hecho en alguna de las acti-
vidades y aplicarlo.
Pr´ctica 1.
a
Objetivo. Aplicaci´n de los conceptos aprendidos hasta este
o
subtema.
Mediante el uso de materiales de uso com´n, realizar medi-
u
ciones directas e indirectas.
Aplicar la teor´ de errores para la expresi´n de los resultados
ıa o
y mediciones.
Experimento 1: Medici´n Directa.
o

100. 88 Introducci´n al Conocimiento de la F´
o ısica
Material.
1. Goma para borrar.
2. Una lata de chiles en vinagre.
3. Caja de medicina
4. caja de un litro de leche.
5. Una naranja o bal´n.
o
6. Regla graduada en cent´
ımetros, metro flexible y/o vernier.
´
7. Formulario para el c´lculo de Areas y volumenes.
a
Descripci´n del Procedimiento.
o Observe la forma del cuerpo a
medir, consulte el formulario para que decida que medidas reali-
zar, realicelas y anotelas, cada medida debe tener su unidad de
medida.
Dibuje o fotograf´ los pasos realizados.
ıe
calcule el volumen para cada material utilizado.
Experimento 2: C´lculo de la densidad y el volumen de un cuerpo.
a
(Medici´n Indirecta)
o
Material.
1. Taza o biber´n con unidades de medida en mililitros (aqu´ se
o ı
le llamar´ recipiente indistintamente)
a
2. Una piedra que pueda entrar en el recipiente.
3. una pelota de pl´stico.
a

101. 1.2 Magnitudes F´
ısicas y su Medici´n.
o 89
4. Una canica “tombola”.
5. Balanza granataria o b´scula electr´nica (aqu´ se le lla-
a o ı
mar´ balanza indistintamente).
a
Descripci´n del Procedimiento.
o Medir en la balanza la masa de
la piedra, anotarla. Vaciar agua en el recipiente, anotando el
valor en ml. colocar la piedra dentro del recipiente midiendo el
volumen final anotarlo.
Con ´stos datos calcular la densidad del cuerpo expresandola
e
g g kg
en ml , cm3 y m3 ..
Realice lo mismo pero ahora con la “tombola”.
Dibuje o fotograf´ los pasos realizados.
ıe

102. 90 Introducci´n al Conocimiento de la F´
o ısica
Indicaciones para el Reporte.
1. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
2. Se entregar´ un reporte por equipo.
a
3. El reporte de la pr´ctica debe contener:
a
* Presentaci´n. o
* Introducci´n. o
* Desarrollo.
* Conclusiones.
* Bibliograf´ ıa.
4. Discuta en equipo el contenido de cada uno de los puntos
que debe contener el reporte
5. Para el paso llamado desarrollo, tomar como base en la
pr´ctica personal realizada:
a
6. Reunirse en equipo e intercambiar datos y opiniones sobre
los experimentos realizados.
a) Proceder en el orden en que se enumer´ el material.
o
b) si alg´n material no tiene la misma forma o tama˜o,
u n
realizar la medici´n nuevamente, de manera que no haya
o
diferencias.
c) como son cinco integrantes deben reportarse cinco me-
diciones.
d ) Anotar la descripci´n de los pasos numer´ndolos, por
o a
ejemplo:
1.- Se observ´ que la goma es rectangular por lo que se
o
necesitan tres medidas, largo ancho y altura.
2.- La atura se midi´ con el . . . , porque;
o
3.- El ancho es: . . .
4.- . . . . . .
5.- El c´lculo del volumen es . . . porque tiene la forma:
a
....
e) Realizar un cuadro donde se presenten las mediciones y
c´lculos realizados.
a
f ) Discuta en equipo el contenido de las conclusiones y la
bibliograf´ ıa.

103. 1.3 Vectores. 91
Para la evaluaci´n de la Pr´ctica 1 se tomar´ en cuenta:
o a a
1. Entrega en tiempo y forma (dos semanas m´ximo).
a
2. Validez y pertinencia de las ideas expuestas.
3. Profundidad de los conceptos.
4. Revisi´n del contenido.
o
5. Presentaci´n al profesor por el coordinador.
o
6. habra una coevaluaci´n por lo que se debe poner de acuerdo
o
con el profesor.
7. La evaluaci´n se reportar´ en un cuadro como el siguiente:
o a
Indicador si no ponder. calif.
Present´ en tiempo y forma
o 1
El reporte contiene
Introducci´n o 1
Desarrollo 2
Conclusiones 1
bibliograf´ıa 1
existe Validez y pertinencia 1
de las ideas expuestas
Existe Claridad y coherencia 1
en el escrito.
Existe Profundidad en los 2
conceptos
1.3. Vectores.
1.3.1. Diferencia Entre las Magnitudes Escalares y Vec-
toriales.
En la vida real, existen diferentes tipos de cantidades en es-
pecial, para la f´
ısica, dos tipos son importantes.
Cantidades Escalares
Quedan totalmente especificadas si se conoce:

104. 92 Introducci´n al Conocimiento de la F´
o ısica
1. El n´mero de objetos de que se trata.
u
2. Unidad de medida de los objetos.
Ejemplo:
22 alumnos
50 butacas
20 kilogramos
3 cm3
10 · lapiceros
n´mero
u unidad
Cantidades Vectoriales
Este tipo de cantidades requieren de mayor especificaci´n, es
o
decir contestar la pregunta “hacia donde”, a esas cantidades se
les debe asignar una direcci´n y un sentido, por lo tanto pa-
o
ra que queden completamente especificadas, se necesitan cuatro
caracter´
ısticas;
1. N´mero
u
2. Unidad de medida
3. Direcci´n
o
4. Sentido

105. 1.3 Vectores. 93
Ejemplo:
Lanzar
Acelerar
Velocidad
Desplazamiento
Girar
Campo Magn´tico
e
Campo El´ctrico
e
Representaci´n de una Cantidad Vectorial.
o
Estas cantidades se representan en F´
ısica:
Por medio de l´ ıneas rectas con una punta de
flecha, a las cuales se les llama vectores.
1.3.2. Caracter´
ısticas de un Vector.
Las caracter´
ısticas de los vectores son:

106. 94 Introducci´n al Conocimiento de la F´
o ısica
a) Longitud de la l´ınea; indica magnitud
(n´mero y unidad) de la cantidad vectorial.
u
b) Inclinaci´n con respecto a la horizontal; indica
o
la direcci´n del vector y se expresa por medio
o
de un ´ngulo.
a
c) Punta de la flecha; indica el sentido del vec-
tor.
.
Figura 1.11: Vector y sus Caracter´
ısticas: O: Origen, F: Sentido, θx : Direcci´n,
o
X: Eje de Referencia.
−→
En la figura: 1.11 OF indica la Magnitud del vector.
Notaci´n.
o
Los vectores se representan con letras,
→
−
a, a, a, ab, a, A
˜ ˆ (1.7)

107. 1.3 Vectores. 95
1.3.3. Representaci´n Gr´fica de Sistemas de Vectores.
o a
En el Plano de acci´n
o
Coplanares: Vectores que act´an sobre un mismo plano, forma-
u
do por dos ejes ortogonales de coordenadas: x vs y, x vs z, y vs
z.
Vectores Coplanares Vectores No Coplanares
Vectores Concurrentes Vectores no Concurrentes
Figura 1.12: Clasificaci´n de Vectores 1
o
No coplanares: Vectores que act´an en planos distintos. Los
u
ejes de referencia ser´n los ejes de coordenadas x, y, z.
a

108. 96 Introducci´n al Conocimiento de la F´
o ısica
En Direcci´n de su Recta de Acci´n
o o
Concurrentes: Sus rectas de acci´n se cortan en alguna parte
o
en el plano
Colineales: Act´an sobre la misma recta de acci´n
u o
Vectores Colineales Vectores Paralelos
Figura 1.13: Clasificaci´n de Vectores 2
o

109. 1.3 Vectores. 97
Paralelos:Dos o m´s vectores cuyas rectas de acci´n tienen la
a o
misma direcci´n.
o
Principio de Transmisibilidad.
Basado en las condiciones de los vectores deslizantes, los cua-
les son vectores que se pueden mover sobre su l´ ınea de acci´n,
o
establece que:
El efecto externo de un vector en un cuerpo r´
ıgi-
do, es el mismo para todos los puntos de aplicaci´n,
o
a lo largo de su l´ınea de acci´n. Sin embargo, su
o
efecto interno depende directamente del punto de
aplicaci´n del vector sobre el cuerpo.
o
Figura 1.14: Proceso que sufre un vector al actuar en un cuerpo por el prin-
cipio de transmisibilidad.
Ejemplo 1.3.3.1
Dibuje un vector de 20uv a 30◦ hacia arriba a la derecha.
Utilice una escala adecuada.

110. 98 Introducci´n al Conocimiento de la F´
o ısica
Soluci´n:
o
Aplicar el siguiente procedimiento:
Procedimiento. 1.3.3
Paso 1. Se miden con el transportador los grados.
Para este caso: 30◦ .
Paso 2. Se toma una escala.
p. e. para este caso: 1cm = 4uv ⇒ 5cm =
20uv.
Paso 3. Se traza una l´ ınea recta con esta medida en
direcci´n del ´ngulo medido.
o a
Paso 4. Se dibuja la punta de flecha en el extremo de la
l´
ınea trazada, teniendo cuidado de no exceder
su medida.
Figura 1.15: v 20 uv 30◦ ր. Ejemplo: 1.3.3.1

111. 1.3 Vectores. 99
Ejemplo 1.3.3.2.
Un avi´n viaja hacia el este a 600 km . Utilice una escala ade-
o hr
cuada para dibujar el vector velocidad que lleva el avi´n.
o
Soluci´n:
o
Aplicando el procedimiento: 1.3.3
Figura 1.16: 600 km →, figura para el ejemplo: 1.3.3.2.
hr
1.3.4. Descomposici´n y Composici´n de Vectores M´to-
o o e
dos Gr´ficos y Anal´
a ıticos.
Igualdad de Vectores.
Dos vectores son iguales si y solo si:
a). Tienen la misma magnitud
b). La misma direcci´n y
o
c). El mismo sentido

112. 100 Introducci´n al Conocimiento de la F´
o ısica
Un vector que tiene la misma magnitud que otro
pero va en sentido contrario constituye el vector
negativo del primero.
Figura 1.17: Igualdad de Vectores.
Figura 1.18: Vector Negativo de A.

113. 1.3 Vectores. 101
Actividad. 1.3.4
1. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
2. Responda las siguientes preguntas:
a) Mediante un diagrama; ¿Es posible demostrar la igual-
dad de vectores?
b) ¿y que un vector sea el negativo de otro?
c) Utilice los resultados de la actividad 3.1.7.1.
3. Aplicar al tema el Metodo Cient´ ıfico.
4. para la evaluaci´n se tomar´ en cuenta:
o a
a) Entrega en tiempo y forma (una semana m´ximo).a
b) Claridad en el escrito presentado.
c) Coherencia de lo escrito con las preguntas realizadas.
d ) Argumentos de la demostraci´n. o
e) Demostraci´n de las preguntas.
o
Suma de Vectores.
Su representaci´n algebr´ica es:
o a
R=A+B (1.8)
Para realizar este proceso de forma gr´fica, se realizan los si-
a
guientes pasos:

114. 102 Introducci´n al Conocimiento de la F´
o ısica
Procedimiento: 1.3.4 Suma de Vectores
Paso 1. Dibujar los vectores de acuerdo a sus carac-
ter´
ısticas.
Paso 2. Trasladar un vector al extremo del otro.
Paso 3. Cerrar el triangulo trazando una l´ ınea. desde
el inicio del vector base hasta el extremo del
vector trasladado.
Paso 4. El vector suma o resultante est´ representado
a
por esta l´
ınea.
Paso 5. medir y expresar el valor del vector suma en
sus unidades correspondientes.
Ejemplo 1.3.4.1 Una persona se mueve 4 pasos hacia la derecha,
luego 3 pasos m´s. Utilice una escala adecuada.
a
Soluci´n
o
1. Aplicando el procedimiento 1.3.4
2. Haga un diagrama descriptivo del problema.
3. Realice las representaciones de los vectores para cada n´me-
u
ro de paso.
4. la escala es: 1cm = 1 paso.
5. El vector resultante est´ representado por la l´
a ınea trazada
desde el inicio del primer vector hasta el final del segundo.

115. 1.3 Vectores. 103
Figura 1.19: Suma de Vectores, indicando el N´mero del paso Realizado.
u
6. medir y expresar el valor del vector suma en sus unidades
correspondientes.
Ejemplo 1.3.4.2 Una persona se mueve 10 pasos hacia el nores-
te, luego 7 pasos hacia el sureste, resuelva el problema utilizando
una escala adecuada.
Soluci´n
o
1. Haga un diagrama descriptivo del problema.
2. Realice las representaciones de los vectores para cada n´me-
u
ro de pasos.
3. la escala es: 1cm = 1 paso.

116. 104 Introducci´n al Conocimiento de la F´
o ısica
Figura 1.20: Soluci´n del Ejemplo 1.3.4.1 V1 = 4 pasos V2 = 3 pasos, R =
o
V1 + V2 = 7 pasos →.
4. El vector resultante est´ representado por la l´
a ınea trazada
desde el inicio del primer vector hasta el final del segundo.
5. medir y expresar el valor del vector suma en sus unidades
correspondientes.
Figura 1.21: Soluci´n al Ejemplo 1.3.4.2 V1 = 10pasos ր, V2 = 7pasos ց,
o
R = V1 + V2 = 12,3 pasos 10◦ ր
Resta de Vectores.
Su representaci´n algebr´ica es:
o a
R=A−B (1.9)

117. 1.3 Vectores. 105
se realizan los siguientes pasos:
Procedimiento 1.3.4 Resta de vectores
Paso 1. Dibujar los vectores de acuerdo a sus carac-
ter´
ısticas.
Paso 2. Cambiar el sentido al vector a restar.
Paso 3. Trasladar un vector al extremo del otro.
Paso 4. Cerrar el triangulo trazando una l´ ınea desde
el inicio del vector base hasta el extremo del
vector trasladado.
Paso 5. El vector resta o resultante est´ representado
a
por esta l´
ınea.
Paso 6. medir y expresar el valor del vector suma en
sus unidades correspondientes.
M´todo del Pol´
e ıgono.
Se utiliza para encontrar la resultante gr´fica de m´s de dos
a a
Vectores.

118. 106 Introducci´n al Conocimiento de la F´
o ısica
Procedimiento: 1.3.4 M´todo del Pol´
e ıgono
Paso 1. Se coloca un vector a continuaci´n de otro, con-
o
servando sus caracter´ ısticas: magnitud, direc-
ci´n y sentido.
o
Paso 2. La resultante se traza del punto de aplicaci´n
o
del primer vector al extremo del ultimo traza-
´
do.
Paso 3. El sentido de la resultante ser´ desde el origen
a
del primer vector al ultimo vector trazado.
´
Figura 1.22: Resta de Vectores, Indicando el N´mero del paso Realizado.
u

119. 1.3 Vectores. 107
Figura 1.23: Suma de Vectores por el M´todo del Pol´
e ıgono

120. 108 Introducci´n al Conocimiento de la F´
o ısica
Figura 1.24: Resultante de la suma de los vectores de la figura: 1.23 por el
M´todo del Pol´
e ıgono

121. 1.3 Vectores. 109
Teorema de Pit´goras. En la Suma y Resta de Vectores Mutua-
a
mente Perpendiculares.
Un vector se puede representar como un par de n´meros en
u
el plano cartesiano, p. e. A(x, y)
Figura 1.25: Representaci´n de un Vector y sus Componentes Rectangulares
o
Como se observa en la figura 1.25, se forman dos tri´ngulos
a
los cuales tienen dos lados perpendiculares entre si, es decir for-
man 90◦ , por lo que son tri´ngulos rectangulos. Los lados que
a
◦
forman el ´ngulo de 90 se llaman catetos y la diagonal que los
a
une; hipotenusa. Los Babilonios conoc´ este triangulo y en-
ıan
contraron una relaci´n entre los lados, esta relaci´n fue hecha
o o
famosa por el griego Pit´goras de Samos por quien se conoce
a

122. 110 Introducci´n al Conocimiento de la F´
o ısica
como Teorema de Pit´goras. Establece que: La suma de los cua-
a
drados de los Catetos (del gr. κ´ τ ǫτ oς perpendicular, l´
α ınea que
cae a plomo) es igual a la hipotenusa al cuadrado
` ν o` ´ν
Figura 1.26: Hipotenusa del gr. υ ιπoτ ǫηo`ςα ´ υ πoτ ǫλ`ω fijar, sujetar fuer-
temente una cosa a otra
V 2 = Vx2 + Vy2 (1.10)
Ejemplo: 1.3.4.1 Cuanto vale el vector A si est´ representado
a
por las cordenadas A(3,2)
A2 = A2 + A2
x y
A2 = 32 + 22
A2 = 9 + 4 = 13
√ √
A2 = 13
√
A = 13

123. 1.3 Vectores. 111
el angulo que forma con el eje horizontal se encuentra mediante:
Ay
θ = tan−1 (1.11)
Ax
2
θ = tan−1
3
θ = 33o 41′
Ejemplo: 1.3.4.2Se tiene un vector A representado por el par
de n´meros A(3,4)
u
1. ¿Cual es su representaci´n?
o
2. ¿Cual es su direcci´n con el eje horizontal?
o
El angulo que forma se encuentra mediante:
Ay
θ = tan−1
Ax
4
θ = tan−1
3
θ = 53◦ 7′ 48′′
3. ¿cual es su magnitud?
A2 = A2 + A2
x y
A2 = 32 + 42
A2 = 9 + 16 = 25
√ √
A2 = 25
su magnitud es:
A=5

124. 112 Introducci´n al Conocimiento de la F´
o ısica
Figura 1.27: Figura para el Ejemplo 1.3.4.2.

125. 1.3 Vectores. 113
Suma por Vectores Unitarios.
Las cantidades vectoriales tambi´n se expresan en t´rminos
e e
de vectores unitarios.
Un vector unitario es un vector sin dimensio-
nes que tiene magnitud igual a uno. Sirven para
especificar una direcci´n determinada. Se usan los
o
s´ ı,  ˆ
ımbolos ˆ ˆ y k para representar vectores unitarios
que apuntan en las direcciones x, y y z positivas,
respectivamente.
Ahora V puede escribirse
V = Vxˆ + Vyˆ
ı  (1.12)
Si es necesario sumar el vector A = Axˆ + Ayˆ con el vector
ı 
B = Bxˆ + Byˆ, se escribe:
ı 
R = A + B = Axˆ + Ayˆ + Bxˆ + Byˆ = (Ax + Bx )ˆ + (Ay + By )ˆ
ı  ı  ı 
Las componentes de R = A + B son Rx = Ax + Bx y Ry =
Ay + By

126. 114 Introducci´n al Conocimiento de la F´
o ısica
Preguntas
tema 1.2.7.La precisi´n de los instrumentos de medici´n tipos de
o o
errores
1. ¿Qu´ es un error?
e
a) una mala determinaci´n
o b) un mal se˜alamiento
n
c) Algo improbable. d) a) y b) e) ninguna es cierta
2. ¿Cu´ntos tipos de errores hay?
a
a) 10 b) 5 c) 7 d) 20
3. Se clasifica en cuatro clases instrumentales, ambientales y
sistem´ticas.
a
a) de Calibraci´n.
o b) Sistem´ticos.
a c) de Esca-
la.
4. ¿Se deben a variables no controlados?
a) Por defecto b) Ambientales c) Aleatorias
5. ¿Es la suma de todos los valores medidos?
a) Aproximaci´n
o b) Error. c) Valor
6. ¿Como se le conoce a los valores medidos dividida por el
n´mero de valores?
u
a) Aproximaci´n verdadera o valor medio.
o b) Aproxi-
maci´n
o c) Valor.
7. ¿En donde se da el valor relativo?
a) Porcentaje. b) Medici´n
o c) Aproximaci´n
o
8. Medir es comparar ¿Como se puede hacer?
a) Directo. b) indirecto. c) Exacto

127. 1.3 Vectores. 115
9. Errores en la medici´n son constantes y se clasifican:
o
a) Por defecto o instrumentales b) Comparaci´n y me-
o
dici´n
o c) Valor o porcentaje.
10. ¿Qu´ es un error en la medida?
e
a) Una cantidad b) Valor c) Aproximaci´n.
o
1.3.1. Diferencia entre las magnitudes escalares y vectoriales.
1. ¿Para la f´
ısica cuales tipos de cantidades son importantes?
a) Cantidades escalares y vectoriales. b) N´mero y di-
u
recci´n.
o c) Correcto e incorrecto. d) Fundamenta-
les y derivadas.
2. ¿22 alumnos a que tipo de cantidad pertenece?
a) Cantidades vectoriales b) Cantidades escalares c)
Prefijo d) Coplanar.
3. ¿Como se llaman los vectores que act´an sobre un mismo
u
plano, formado por dos ejes ortogonales de coordenadas?
a) Concurrente b) No Coplanar. c) Coplanares.
d) Angulares
4. Son ejemplos de magnitudes vectoriales.
a) Masa y peso b) Longitud y peso c) Fuerza y
masa d) Desplazamiento y velocidad
5. Dos vectores son iguales cuando tienen la misma direc-
ci´n, magnitud y: a) Naturaleza
o ´
b) Area c) Senti-
do d) Principio

128. 116 Introducci´n al Conocimiento de la F´
o ısica
6. Como se llaman las cantidades que se sabe el n´mero de
u
objetos y la unidad de medida de los objetos.
a) Escalares b) Colineales c) Libres d) Cir-
cunstanciales
7. Se representan por medio de l´
ıneas con una punta de flecha,
las cuales se llaman:
a) T´rmino
e b) Principio c) Vectores d) Erro-
res
8. Son dos o m´s vectores cuyas rectas de acci´n tienen la
a o
misma direcci´n.
o
a) Paralelos b) Colineales c) Perpendicular d)
Iguales
9. Son los vectores que act´an sobre la misma recta de acci´n:
u o
a) Concurrentes b) Paralelos c) Colineales d)
Aceleraci´n
o
10. Son los vectores en los cuales sus rectas de acci´n se corta
o
en alguna parte del plano.
a) Colineales b) Coplanares c) Concurrentes d)
No coplanares
1.3.2.Caracter´
ısticas de un vector.
1. Es todo segmento de recta dirigido en el espacio:
a) Vector b) Sentido c) Origen
2. Al origen tambi´n se le denomina.
e
a) Espacio b) Vector c) Punto de aplicaci´n
o

129. 1.3 Vectores. 117
3. Viene dada por la orientaci´n de la recta que lo contiene:
o
a) M´dulo
o b) Direcci´n
o c) Origen
4. Es la longitud o tama˜o de un vector y debes medir desde
n
su origen hasta su extremo
a) M´dulo
o b) Direcci´n
o c) Sentido
5. Indica hacia qu´ lado de la l´
e ınea de acci´n se dirige el vector.
o
a) Sentido b) Origen c) M´dulo
o
6. Cuando dos vectores tienen el mismo m´dulo y la misma
o
direcci´n son:
o
a) vectores libres b) vectores iguales c) suma de
vectores
7. Que vector es caracterizado por su m´dulo direcci´n y sen-
o o
tido.
a) Vector igual b) vector libre c) vector indepen-
diente
8. Cuantas caracter´
ısticas importantes tiene un vector:
a) 3 b) 9 c) 5
9. Con el vector se forman:
a) rectas b) segmentos c) las dos anteriores
10. En que materia se utiliza el vector a) Qu´
ımica b) F´
ısica
c) Matem´ticas
a d) todas las anteriores

130. 118 Introducci´n al Conocimiento de la F´
o ısica
1.3.3.Representaci´n gr´fica de sistemas de vectores Coplanares,
o a
deslizantes, libres colineales y concurrentes.
1. ¿Qu´ son los vectores coplanares?
e
a) Son los vectores que act´an en planos distintos.
u b)
Vectores que act´an sobre un mismo plano.
u c) Son vec-
tores no tienen caracter´
ısticas.
2. ¿Qu´ son los paralelos?
e
a) Son dos o m´s vectores cuyas rectas de acci´n tienen la
a o
misma direcci´n. b) Son vectores lineales.
o c) En direc-
ci´n de su recta de acci´n.
o o
3. ¿Qu´ son los concurrentes?
e
a) Sobre la misma recta de acci´n
o b) Son vectores des-
lizantes. c) Son rectas de acci´n se cortan en alguna
o
parte del plano.
4. ¿Qu´ son los colineales?
e
a) Act´an sobre la misma recta de acci´n.
u o b) Se cor-
tan en alguna parte del plano. c) En direcci´n de su
o
recta.
5. ¿Cu´l es su efecto interno de un vector?
a
a) En un cuerpo ligero b) Depende directamente del
punto de aplicaci´n del vector sobre el cuerpo.
o c) Des-
lizante que establece el efecto.
6. ¿Cu´les son las condiciones de los vectores deslizantes?
a
a) Punto de aplicaci´n.
o b) Su efecto interno. c)
Establece que el efecto externo de un cuerpo r´
ıgido.

131. 1.3 Vectores. 119
7. ¿Como se clasifican los coplanares?
a) Coplanares, no coplanares. b) Coplanares en plano.
c) Coplanares y vectores.
8. ¿Cu´les son los cuatro tipos de vectores?
a
a) Vectores internos, externos y concurrentes.
Problemas
1. Encuentre por el m´todo gr´fico y anal´
e a ıtico las componen-
tes rectangulares o perpendiculares de los siguientes vecto-
res:
o
a) V1 = 33T 50 ր
Respuesta V1X = 21,212T
V1Y = 25,278T
b) V = 2,5 N 35
C
o
տ
Respuesta Vx = −2,048 N
C
Vy = 1,434 N
C
m o
c) V = 200 s2 60 ւ
m
Respuesta Vx = −100 s2
m
Vy = −173,2 s2
2. Las componentes de un vector son Ax = 10 m y Ay = 6 m.
¿Qu´ ´ngulo forma este vector con el eje x positivo?
ea

132. 120 Introducci´n al Conocimiento de la F´
o ısica
3. Calcule las componentes rectangulares de los vectores A
que, estando contenidos en el plano x e y, forman un ´ngulo
a
θ con el eje x, para los siguientes valores del m´dulo de A
o
yθ:
(a) A = 10T, θ = 30◦ ;
(b) A = 5 N , θ = 45◦ ;
C
(c) vecA = 7km, θ = 60◦ ;
m
(d) A = 5 s2 , θ = 90◦
(e) A = 15 km , θ = 150◦ ;
hr
(f ) A = 10 m , θ = 240◦
s
m
(g) A = 8 s2 , θ = 270◦ .
4. Un vector A tiene la magnitud de 8 m y forma un ´nguloa
de 37 ◦ con el eje X. Si los vectores B y C se expresan como
B = (3ˆ − 5ˆ) m y C = (6ˆ + 3ˆ) m, determine:
ı  ı 
(a) exprese el vector A en la forma: A = (axˆ − ayˆ) m
ı 
(b) D = A + C;
(c) E = B − A;
(d) F = A − 2B + 3C;
(e) un vector G tal que G − B = A + 2C + 3G.

133. Movimiento
“Los cient´ficos se resist´an a creer
ı ı
que todos los cuerpos c´en a la misma velocidad.
a
Fue f´cil convencerlos: las piedras de diferente tama˜o
a n
arrojadas desde lo alto de la torre de Pisa
llegaron al mismo tiempo,
aunque, por supuesto sus pesos eran muy diferentes.”
GALILEO GALILEI
La ca´ de los Cuerpos.
ıda
Galileo Galilei. Libro de Galileo (1610).

134. 122 Movimiento
2.1. Movimiento en una Dimensi´n
o
2.1.1. Conceptos Fundamentales.
Definici´n:
o
Cinem´tica (gr. κιηεµα (kinema): movimiento)
a
Parte de la mec´nica (gr. µεκ´ ηε: mekane:) que se
a α
encarga de estudiar el movimiento sin explicar las
causas del movimiento.
¿Que Estudia la Cinem´tica?
a
Estudia y explica como se mueven los cuerpos.
La Cinem´tica; Estudia los movimientos de los cuerpos in-
a
dependientemente de las causas que lo producen.
Es decir que describe la forma o manera en que se mueven
los cuerpos, pero no explica porque se mueven asi.
Movimiento Relativo.
Depende del punto desde donde se observa el movimiento,
esto es desde el Sistema de Referencia de Observaci´n
o
2.1.2. Sistemas de Referencia (SR).
Es el punto desde donde se observa un movi-
miento.

135. 2.1 Movimiento en una Dimensi´n
o 123
Existen dos tipos, Sistema de Referencia Inercial (SRI) y Sis-
tema de Referencia No-Inercial (SRNI)
Sistema de Referencia Inercial (SRI).
Un Sistema de Referencia Inercial (SRI), es
aquel que se mueve con velocidad constante con
respecto a otro.
Un ejemplo de sistema de referencia inercial puede ser un tren
que se mueve en un tramo de v´ rectil´
ıa ıneo con una velocidad
constante.
Sistema de Referencia No Inercial (SRNI).
Un Sistema de Referencia No-Inercial (SRNI)
se mueve con respecto a otro con una aceleraci´n.
o
La propia Tierra constituye un sistema de referencia no iner-
cial, ya que gira con una aceleraci´n normal, que si bien es pe-
o
que˜a, en ciertos fen´menos se observa con claridad, pero que a
n o
velocidades peque˜as se considera Sistema de Referencia Iner-
n
cial.
En la mayor´ de los trabajos f´
ıa ısicos y de ingenier´ se consi-
ıa
dera inercial cualquier sistema ligado a la superficie de la Tierra,
la cu´l evidentemente no est´ quieta ni movi´ndose en forma rec-
a a e
til´
ınea y uniforme, sin rotaci´n, pero el error que se comete al
o
considerarlo como Inercial es insignificante.

136. 124 Movimiento
Los sistemas de referencia en f´
ısica se representan mediante
los sistemas de coordenadas.
Algunos de los m´s usados son :
a
El sistema de coordenadas cartesiano rectangular en dos y
tres dimensiones
El sistema de coordenadas polares en dos dimensiones
El sistema de coordenadas cil´
ındricas en tres dimensiones
El sistema de coordenadas esf´ricas en tres dimensiones
e
Preguntas
1. ¿Cu´ntos tipos de sistema de referencia existen ?
a
2. ¿Qu´ quiere decir SRI?
e
3. ¿Qu´ quiere decir SR?
e
Figura 2.1: Observaci´n de un Movimiento y su Vector de Posici´n (r)
o o

137. 2.1 Movimiento en una Dimensi´n
o 125
4. ¿Que significado tiene la abreviaci´n: SRNI
o
5. ¿C´mo es la velocidad del SRI?
o
6. De un ejemplo de SRI
7. De un ejemplo de SR
Figura 2.2: Sistema de Referencia en Tres Dimensiones

138. 126 Movimiento
Posici´n, Distancia, Desplazamiento
o
El estudio del movimiento requiere que se conozcan algunos
conceptos necesarios para su estudio, los m´ınimos son los si-
guientes:
Posici´n.
o
Punto donde se encuentra ubicado un cuerpo,
el cual se introduce en un eje de coordenadas.
Trayectoria.
Curva que realiza un cuerpo al moverse.
Distancia
Magnitud escalar que se encuentra midiendo la
longitud de la trayectoria.

139. 2.1 Movimiento en una Dimensi´n
o 127
Desplazamiento.
Vector trazado desde el punto donde se comien-
za la observaci´n del movimiento hasta dode se deja
o
de observar.
Figura 2.3: Vectores de Posici´n (ri ) y Desplazamiento (D = ∆r = r2 − r1 )
o
Ejemplo 2.1.2
Sobre una barca que se mueve sobre un rio viajan 2 personas,
sobre la orilla se encuentra otra persona que observa a la barca.
El rio se mueve recorriendo dos km en cada minuto y sobre
la barca una persona rema, y la otra se mueve sobre la barca
recorriendo los cuatro metros que mide la barca en 10 segundos.
a). Haga un diagrama que describa el problema.
b). ¿Que longitud tiene la barca?

140. 128 Movimiento
Figura 2.4: Figura para el problema: 2.1.2
R: 4 m
c). ¿Cuantos sistemas de referencia existen en este problema?
R: Tres
d). ¿Que distancia recorre el rio?
2 Kilometros en 60 s.
e). ¿Que trayectoria describe el rio respecto:
e.1. El observador de la orilla.
R: Una l´
ınea recta que se aleja de el hacia adelante.
e.2. El observador que rema.

141. 2.1 Movimiento en una Dimensi´n
o 129
R: Una l´
ınea recta que se aleja de el hacia atr´s.
a
e.3. El observador que se mueve sobre la barca
R: Una l´
ınea recta que se aleja hacia atr´s de el.
a
Preguntas
1. ¿Qu´ es el desplazamiento?
e
2. ¿Qu´ es la posici´n?
e o
3. Significado de distancia
4. Significado de trayectoria
Velocidad
2.1.3. Movimiento Rectilineo Uniforme (MRU).
Para este caso, la trayectoria es una l´
ınea recta.
La distancia y el desplazamiento coinciden.
La posici´n se puede representar por un punto sobre la l´
o ınea
de la trayectoria.
Figura 2.5: Posici´n (r), Distancia (x) y Desplazamiento (d = ∆r = ∆x) en
o
un Movimiento Rectilineo

142. 130 Movimiento
Caracter´
ısticas del MRU
a). La trayectoria es una l´
ınea recta.
b). El cuerpo recorre distancias iguales en tiempos
iguales.
c). La gr´fica distancia contra tiempo (d o x vs t)
a
es una l´
ınea recta.
d). La divisi´n de la distancia (d) entre el valor
o
del tiempo (t), es la rapidez y es un valor igual
para cada punto.
Velocidad:
Cociente entre el Desplazamiento (d) medido en
[m]etros y el tiempo medido en [s]egundos en el
Sistema Internacional de Unidades (SI).
d
v=v= (2.1)
t
de la figura 2.5:
d = ∆r = r2 − r1

143. 2.1 Movimiento en una Dimensi´n
o 131
r2 − r1
⇒v= (2.2)
t2 − t1
la que para el Movimiento Rectil´
ıneo (MR) queda:
x2 − x1 ∆x
v= = (2.3)
t2 − t1 ∆t
Rapidez.
Cociente entre la distancia (d) medida en [m]etros y el tiempo
(t) medido en [s]egundos en el Sistema Internacional de Unida-
des (SI).
d
r = |v| = (2.4)
t
de acuerdo a la figura 2.5, x = d por lo que:
x m
r= (2.5)
t s
en el Sistema Internacional.
De lo anterior, se debe notar que:
La rapidez es una cantidad escalar y la velocidad es una can-
tidad vectorial.
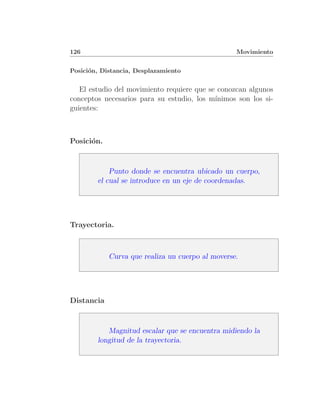
La gr´fica de la posici´n (x ´ d) contra el tiempo es de la
a o o
forma 2.6 en la p´gina 132. Tambi´n se puede ver la gr´fica; 6.2
a e a
en la p´gina 303
a

144. 132 Movimiento
Figura 2.6: Gr´fica del Movimiento Rectil´
a ıneo Uniforme (MRU).

145. 2.1 Movimiento en una Dimensi´n
o 133
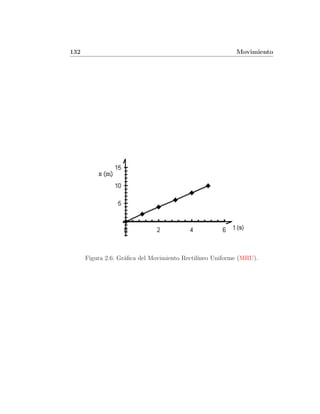
Ejemplo: 2.1.3.1 Se suelta un bal´ desde una rampa, al final de
ın
esta, se toma como el inicio del movimiento, en l´
ınea recta hori-
zontal, se midieron los valores de tiempo y distancia recorridos,
los que se presentan en el cuadro: 2.1.
d [m] t [s] r = d[m]
t s
0 0 —
2 1 2
4 2 2
6 3 2
8 4 2
10 5 2
12 6 2
14 7 2
Cuadro 2.1: Tabla de datos del ejemplo: 2.1.3.1
Figura 2.7: Gr´fica d vs t para el ejemplo: 2.1.3.1.
a
Velocidad Promedio.
La rapidez promedio se encuentra sumando los valores de las
velocidades y se divide entre el n´mero de velocidades
u

146. 134 Movimiento
n
ri
i=1
r =r=
¯ (2.6)
n
Ejemplo: 2.1.3 En un veloc´ ımetro de automovil, se obtuvieron
los siguientes valores de rapidez: 40 km , 80 km , 60 km , 70 km , 90
hr hr hr hr
km
hr .
¿Cual es la rapidez media o promedio?
aplicando la relaci´n (2.6)
o
40 km +80 km +60 km +70 km +90 km 340 km
r = hr hr
5
hr hr hr
= 5
hr
= 68 km
hr
m
¿Cuanto es esta rapidez en s?
68km
ր 1000m 1hr
ւ
1hr
ւ · 1km
ր · 3600s = 68000m
3600s =18.89 m
s
Velocidad Instantanea.
En general, la velocidad de un cuerpo, var´ de instante en
ıa
instante, el valor que toma en cualquier instante es la velocidad
instantanea.
La noci´n de instante es una abstracci´n, pero es posible
o o
realizar una aproximaci´n a este concepto, considerandolo como
o
un intervalo de tiempo peque˜isimo, (asi lo hizo Newton) asi
n
el instante es una millon´sima de segundo y ese tiempo puede
e
tomarse como el instante en el que no cambia la magnitud de la
velocidad.
Para indicar un cambio en valor, se utiliza la letra griega
∆ delta, seguida de la letra a la que se le “mide” el cambio,
por ejemplo: ∆x indica que cambi´ la variable x, as´ que para
o ı
variaciones muy peque˜as se pueden expresar, utilizando una
n

147. 2.1 Movimiento en una Dimensi´n
o 135
“d”. Un intervalo de tiempo muy peque˜o, se representar´ por
n a
“dt” y la variaci´n del espacio medio sobre la trayectoria se
o
representa como “dx” de manera que la velocidad instantanea
se escribe:
dx
vi = (2.7)
dt
y se le´:
e
La velocidad instant´nea es la variaci´n de la
a o
posici´n de un cuerpo con respecto al tiempo.
o
Gr´ficas de Movimientos.
a
Cuando un cuerpo se mueve sobre una l´ ınea recta, se produce
un movimiento rectil´ ıneo.
Si su trayectoria es una curva cerrada, es el´ıptico como el de
un planeta o circular como el de las manecillas de un reloj.
Cuando describe una trayectoria en l´ ınea recta y recorre dis-
tancia iguales en tiempos iguales es un Movimiento Rectilineo
Uniforme (MRU), adem´s la velocidad es siempre la misma y su
a
gr´fica es un l´
a ınea recta, como ya se dijo anteriormente.
En la figura 2.8, se presenta la gr´fica x vs t, de un MRU. La
a
figura 2.9, es la gr´fica r vs t, de ese mismo movimiento. El ´rea
a a
sombreada es un rect´ngulo en el que en la parte horizontal
a
se tiene el tiempo y en la vertical la rapidez. El ´rea de un
a
rectangulo se encuentra multiplicando el largo × altura, para
este caso es largo (t) × altura (r) ´ r × t = (r)(t) = r · t, pero r
o

148. 136 Movimiento
m
es la rapidez (que se mide en s y t es el tiempo en s), entonces:
r m t [s] = rt ms = rt [m], es decir la distancia, entonces se
s s
/
/
puede decir que al multiplicar la rapidez por el tiempo se obtiene
la distancia y tambi´n es el ´rea del rectangulo que se forma bajo
e a
la gr´fica de la velocidad (v) o rapidez (r) vs t en un MRU.
a
En un (MRU); la distancia es el ´rea del
a
rect´ngulo que se forma bajo la gr´fica de la ve-
a a
locidad (v) o rapidez (r) vs (t).
Este resultado aunque se obtuvo para el MRU, es v´lido para
a
cualquier movimiento, esto se puede enunciar de manera general
como:
Figura 2.8: Gr´fica d vs t para el MRU
a

149. 2.1 Movimiento en una Dimensi´n
o 137
Figura 2.9: Gr´fica r vs t de la figura 2.8.
a
En un (Movimiento); la distancia es el ´rea bajo
a
la gr´fica de la velocidad (v) o rapidez (r) vs el
a
tiempo (t).
Para el caso del ejemplo 2.9,
m
d= 5 (40 − 5) / = 175m
s
/
s
es la distancia recorrida.
Ejemplo: 2.1.3.1 ¿Aproximadamente a que distancia del DF se
encuentra Hermosillo Sonora si un avi´n tarda 2.5 hrs para llegar
o
y se mueve a una velocidad de crucero de 600 kmhr
representaci´n gr´fica:
o a
r = 600 km
hr
t = 2,5hr
d
r=
t

150. 138 Movimiento
d =?
Sustituyendo:
km d
600 =
hr (2,5hr)
km
⇒d= 600 · (2,5hr
ր)
ր
hr
multiplicando
d = 1500km
Ejemplo: (dificultad media) 2.1.3.2 Una persona sale de un pun-
to a las 8 a m con una rapidez de 15 km , y a las 10 a m sale otra
hr
persona en motocicleta a una rapidez de 50 km ¿A que hora y
hr
lugar se encontrar´n?
a
Soluci´n:
o
La relaci´n del movimiento se puede representar como el de
o
una l´ınea recta de la forma x = vt + b donde v representa la
Figura 2.10: Representaci´n gr´fica para el problema 2.1.3.1
o a

151. 2.1 Movimiento en una Dimensi´n
o 139
velocidad.
Puesto que sale a las 8 a. m. entonces en ese momento su
posici´n es cero y como son dos motocicletas diferentes;
o
km
x1 = 15 t − b1
hr
km
⇒0= 15 (8hr − b1
ր)
ր
hr
⇒ b1 = 120km
La relaci´n general para la 1a motocicleta ser´:
o a
km
⇒ x1 = 15 t − 120km
hr
de manera similar, para la segunda motocicleta:
km
x2 = 50 t − 500km
hr
Figura 2.11: Representaci´n gr´fica para el problema 2.1.3.2.
o a

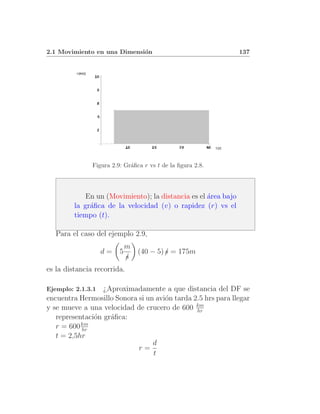
152. 140 Movimiento
Ahora se puede encontrar que la soluci´n gr´fica es el punto
o a
donde se crucen estas l´
ıneas:
Se encuentran en el punto X = 42.855 km, en la hora: 10:
51’26”
De la observaci´n de la gr´fica, entonces, el punto de encuen-
o a
tro es en d =42.855 km, en la hora: 10: 51’ , 26”
Ejemplo: 2.1.3.3 Una persona camina hacia el este como se
muestra en la grafica: 2.12
Figura 2.12: Representaci´n gr´fica del problema 2.1.3.3.
o a
a). ¿Que rapidez adquiri´ entre 0 y 200 m?:
o
(200−0)m m
R: r1 = (11−0)min = 18,18 min
b). En el intervalo de 11 a 19 min ¿que velocidad tiene?:
(200−200)m 0 m m
R: r2 = (19−11)min = 8 min = 0 min
De otra forma: como es una l´ınea paralela al eje t, la rapidez
es cero, por lo que la persona se encuentra en reposo.
c). En el intervalo de tiempo de 19 a 30 minutos:, ¿Que dis-
tancia ha recorrido?
[200−(−100)]m [200+100]m 300m m
R: r3 = (30−19)min = (11)min = 11min = 27,28 min

153. 2.1 Movimiento en una Dimensi´n
o 141
m
por lo que recorre: 28,28 min (11min = 300m
ր ր)
d). En el intervalo de tiempo de 30 a 39 minutos:, ¿Que dis-
tancia ha recorrido?
[0−(−100)]m 100m 100m m
R: r4 = (39−30)min = (9)min = 9min = 11,11 min
m
y recorre: 11,11 min (9min = 100m
ր ր)
Pr´ctica 2.
a
Movimiento Rectilineo Uniforme.
Objetivo. Observaci´n de un Movimiento Rectil´
o ıneo Uniforme
(aproximado).
Aplicaci´n de los conceptos aprendidos hasta este subtema.
o
Mediante el uso de materiales de uso com´n, observar el Mo-
u
vimiento Rectil´
ıneo Uniforme.
Medici´n de distancia y tiempo aplicando las ecuaciones co-
o
nocidas, as´ como, la teor´ de errores para la expresi´n de los
ı ıa o
resultados y mediciones.
Construcci´n del instrumento.
o
Material.
1. Duela de 2. m de longitud.
2. Clavos alfilerillo (15 o m´s).
a
3. Manguera de nivel 1.5 cm de di´metro (o mayor) 2.3 m.
a
4. Canica o bal´ peque˜o.
ın n
5. Agua, aceite o shampoo.

154. 142 Movimiento
6. Dos pedazos de madera cilindricos de diametro igual al de la
manguera (u otro material) que puedan servir como tap´n.o
7. Cron´metro (algunos celulares tienen esta funci´n).
o o
Descripci´n de la Construcci´n.
o o
Dibuje o fotograf´ los pasos realizados.
ıe
Sobre la duela de 2 m, coloque la manguera de manera que
quede lo mas recta posible.
Para que esto sea posible, clave dos alfilerillos a cada lado de
la manguera, cada diez centimetros.
Tape un extremo de la manguera. Llene con el l´ ıquido cui-
dando de poner la canica o bal´ dentro. Tape el otro extremo
ın
de la manguera.
Experimento.
Figura 2.13: Pr´ctica: Movimiento rectil´
a ıneo Uniforme.
Descripci´n del Procedimiento.
o Colocar la manguera sobre una
madera o libro de manera que quede inclinada unos cemt´ ımetros.
inclinar la duela con la manguera, cuidando que la canica quede
en el extremo superior.

155. 2.1 Movimiento en una Dimensi´n
o 143
Medir el tiempo que tarda en pasar los pimeros 10 cm, cui-
dando de que el cron´metro inicie cuando pase por el primer
o
clavo incrustado en la madera.
realice este procedimiento por lo menos cinco veces.
Dibuje o fotograf´ los pasos realizados.
ıe
Indicaciones para el Reporte.
1. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
2. Se entregar´ un reporte por equipo.
a
3. El reporte de la pr´ctica debe contener:
a
* Presentaci´n. o
* Introducci´n. o
* Desarrollo.
* Conclusiones.
* Bibliograf´ ıa.
4. Discuta en equipo el contenido de cada uno de los puntos
que debe contener el reporte
5. Para el paso llamado desarrollo, tomar como base en la
pr´ctica realizada:
a
6. Reunirse en equipo la obtenci´n del material y la construc-
o
ci´n del prototipo.
o
7. Anotar la descripci´n de los pasos numer´ndolos, por ejem-
o a
plo:
1.- Construcci´n. o
2.- Desarrollo
3.-
4.- . . . . . .
5.- Realizar un cuadro donde se presenten las mediciones y
c´lculos realizados.
a
6.- como son cinco integrantes deben reportarse cinco me-
diciones.
7.- Discuta en equipo el contenido de las conclusiones y la
bibliograf´ ıa.

156. 144 Movimiento
Para la evaluaci´n de la Pr´ctica 2 se tomar´ en cuenta:
o a a
1. Entrega en tiempo y forma (Una semana m´ximo).
a
2. Validez y pertinencia de las ideas expuestas.
3. Profundidad de los conceptos.
4. Revisi´n del contenido.
o
5. Presentaci´n al profesor del prototipo por el coordinador.
o
6. Habra una coevaluaci´n por lo que se debe poner de acuerdo
o
con el profesor.
7. La evaluaci´n se reportar´ en un cuadro como el siguiente:
o a
Indicador si no ponder. calif.
Present´ en tiempo y forma
o 1
Present´ el prototipo
o 1
El reporte contiene:
Introducci´n
o 1
Desarrollo 2
Conclusiones 1
Bibliograf´
ıa 1
Existe Validez y pertinencia 1
de las ideas expuestas
Existe Claridad y coherencia 1
en el escrito.
Existe Profundidad en los 1
conceptos
2.1.4. 2a Autoevaluaci´n
o
Nombre del alumno —————————————— Gpo. 30—–
I.- Contesta con la Respuesta Correcta a las Siguientes Pre-
guntas
1. ¿Qu´ es el error de medida?
e
2. ¿C´mo se representa el valor absoluto?
o
3. ¿C´mo se representa el valor verdadero?
o

157. 2.1 Movimiento en una Dimensi´n
o 145
4. ¿C´mo se representa el valor calculado?
o
5. ¿Qu´ es el error sistem´tico?
e a
6. ¿Qu´ es el error aleatorio?
e
7. ¿Que es el error por defecto?
8. ¿Qu´ es el error de escala?
e
9. Este te tipo de error se debe a la simplificaci´n de teor´
o ıas
10. Menciona cual es el tipo de error que se debe cambios im-
prescindibles
11. ¿Se deben al juicio o a la reacci´n de observadores?
o
12. ¿Este tipo de error es la diferencia entre el valor absoluto
y la aproximaci´n?
o
13. ¿Este es el cociente entre el valor absoluto y la aproxima-
ci´n?
o
14. ¿Este tipo de error se presenta en porcentaje?
15. ¿Los errores se deben dar en una cifra significativa de que
manera?
16. ¿Qu´ son las cantidades escalares?
e
17. Menciona 5 ejemplos de cantidades escalares
18. ¿Qu´ son las cantidades vectoriales?
e
19. ¿Caracter´
ısticas tienen las catidades vectoriales?
20. ¿Menciona algunos ejemplos de cantidades vectoriales?

158. 146 Movimiento
21. ¿Menciona las caracter´
ısticas de un vector?
22. ¿Con que letras se representa a los vectores?
23. ¿Sobre que se representan los vectores?
24. ¿En que se basa el principio de transmisibilidad?
25. ¿Cuando son iguales Dos vectores ?
26. ¿Cu´ndo se entiende que es un vector negativo?
a
27. ¿Formula como se representa a la suma de vectores?
28. ¿Formula como se representa a la resta de vectores?
29. ¿C´mo se representa los vectores por n´meros en el plano
o u
cartesiano?
30. ¿Formula el teorema de Pitagoras?
31. ¿Qu´ estudia la cinem´tica?
e a
32. ¿Qu´ es el movimiento relativo?
e
33. ¿Qu´ es sistema de referencia?
e
34. ¿Cu´ntos tipos de sistemas de referencia existen?
a
35. ¿Cual es el Sistema de Referencia Inercial?
36. ¿Cu´l es el Sistema de Referencia No Inercial?
a
37. ¿Ejemplo del SRI?
38. ¿Ejemplo del SNI?
39. ¿Qu´ es posici´n?
e o

159. 2.1 Movimiento en una Dimensi´n
o 147
40. ¿Qu´ es la distancia?
e
41. ¿Qu´ es el desplazamiento?
e
42. ¿Qu´ es la trayectoria?
e
43. ¿Qu´ significa MRU?
e
Menciona algunas caracter´
ısticas de MRU
44. ¿Formula que representa la velocidad?
45. ¿Qu´ es la velocidad?
e
46. ¿Qu´ es la rapidez?
e
47. ¿Qu´ es la velocidad promedio?
e
48. ¿Cu´l es la rapidez media o promedio?
a
49. ¿Qu´ es la velocidad instant´nea?
e a
2a Autoevaluaci´n (continuaci´n)
o o
Nombre del alumno —————————————— Gpo. 30—–
I.- Contesta Correctamente las Siguientes Cuestiones (2 pun-
tos)
1.- De las siguientes magnitudes especifique: V para Vectorial,
E para escalar

160. 148 Movimiento
Cantidad Tipo
a) campo magn´tico
e
b) Carga El´ctrica
e
c) Potencia
d) Diferencia de Potencial
e) Campo El´ctrico
e
f) Fuerza
g) Distancia
h) Desplazamiento
i) Velocidad
j) Rapidez
2.- Deducir las dimensiones de las siguientes cantidades, men-
cionando tambi´n si son Vectoriales (V) o escalares (E)
e
Cantidad Expresi´n Matem´tica Unidades Tipo
o a
r
velocidad = t
Fuerza = ma
long.circunf erencia
π = diametro
catopuesto
sin α = hipotenusa
Campo Electrico E=F q
II.- Resuelva los Siguientes Problemas
1. Por cualquier M´todo gr´fico, obtener la resultante de los
e a
siguientes vectores: F1 = 300N ր, F2 = 500N տ y F3 =
400N ↓
a) Dibuje los vectores
b) Encuentre la resultante

161. 2.1 Movimiento en una Dimensi´n
o 149
a) Dibuje la resultante con magnitud direcci´n y sentido
o
2. Para los vectores V1 = (4ˆ + 3ˆ) N , V1 =
ı  C −5ˆ + 8ˆ
ı j N
C y
V3 = (5ˆ − 4ˆ) N
ı  C
a) Dibuje los vectores
b) Encuentre la resultante por el m´todo anal´
e ıtico
a) Dibuje la resultante con magnitud direcci´n y sentido
o
d) Escriba la expresi´n de la resultante
o
3. Se han tomado los valores de Posici´n y tiempo para una
o
canica que se mueve dentro de un tubo, dando los siguientes
resultados:
Cuadro 2.2: para el problema 3
d m
x[m] t[s] r= t s
0,01 4,3 ± 0,2
0,02 8,4 ± 0,2
0,04 16,7 ± 0,2
0,06 25,2 ± 0,2
0,08 33,4 ± 0,2
0,10 41,7 ± 0,2
a) Realice un dibujo que describa el problema
b) Encuentre el cociente entre x y t para cada punto
c) Dibuje la gr´fica x vs t
a
d) De acuerdo a lo que realiz´ diga si es un MRU, escri-
o
biendo porque lleg´ a tal conclusi´n.
o o

162. 150 Movimiento
Aceleraci´n.
o
El MRU es el caso mas simple del movimiento, pero en la
naturaleza los movimientos no suceden asi, pues la velocidad
cambia tanto en magnitud como en direcci´n, por lo que entra en
o
juego una cantidad llamada aceleraci´n la cual es de naturaleza
o
vectorial tambi´n.
e
Concepto de Aceleraci´n
o
La aceleraci´n se define como El cambio de
o
velocidad dividida por el cambio en el tiempo
en lenguaje de matem´ticas:
a
∆v
a= (2.8)
∆t
2.1.5. Movimiento Rectilineo Uniformemente Acelera-
do (MRUV o MUA).
Cuando la velocidad solo aumenta o disminuye, el movimien-
to se conoce como Movimiento Rectilineo Uniforme Variado
(MRUV), en este caso la velocidad puede aumentar o disminuir,
por ejemplo en la ca´ libre de un cuerpo desde una altura. Este
ıda
caso fue estudiado por Galileo, encontrando que la aceleraci´n
o
que adquiere un cuerpo cayendo desde una altura y lo hace en
m
MRUV con aceleraci´n constante e igual a 9,81 s2
o

163. 2.1 Movimiento en una Dimensi´n
o 151
Ecuaciones del MRUV
Se parte de la relaci´n dada para la aceleraci´n (2.8):
o o
∆v vf − vi
a= =
∆t tf − ti
⇒ a(tf − ti ) = vf − vi
multiplicando;
atf − ati = vf − vi (2.9)
si tf = t, to = 0 y vi = vo , y se sustituyen estos valores en la
relaci´n: 2.9
o
atf − a(0) = vf − vo
at = vf − vo (2.10)
Velocidad Final.
⇒ vf = vo + at (2.11)
Posici´n Final.
o
La velocidad promedio est´ dada por la ec. 2.6 si se toma
a
solo la velocidad inicial vo y la velocidad final (vf ), la velocidad
promedio es:
2
vi vo + vf
v = i=1 = (2.12)
2 2
pero esta es igual a:
x vo + vf
v = =
t 2
vo + vf
⇒ v t= x = t
2

164. 152 Movimiento
o mejor:
vo + vf vo t + vf t
x = t= (2.13)
2 2
pero de 2.11
vf = vo + at
sustituyendo en 2.13:
vo t + (vo + at)t vo t + (vo t + at2 )
x = =
2 2
2vo t + at2 at2
x = = vo t +
2 2
finalmente:
1
x = vo t + at2 (2.14)
2
Velocidad Final En Funci´n de la Posici´n.
o o
Si se toma la expresi´n para la velocidad promedio 2.12
o
x vo + vf
v = =
t 2
vo + vf
⇒ x = t (2.15)
2
de 2.10
at = vf − vo
vf − vo
a=
t
calculando la cantidad:
a·x (2.16)
por ser conveniente en este caso, se tiene:

165. 2.1 Movimiento en una Dimensi´n
o 153
2a · x = (vf − vo ) · (vo + vf )
2 2
2ax = vf − vo (2.17)
2 2
vf − vo = 2ax
en conclusi´n:
o
2 2
vf = vo + 2ax (2.18)
las relaciones: 2.12, 2.13, 2.11, 2.14 y 2.18, son las ecuaciones de
MRUV es conveniente que se escriban en una ficha bibliogr´fica. a
vo+vf
v = 2
vo+vf
x = 2 t
vf = vo + at
x = vot + 1 at2
2
2 2
vf = vo + 2ax
Cuadro 2.3: Ecuaciones del MRUV.
Ejemplos MRUV.
Ejemplo: 2.1.5.1.La velocidad de un auto aumenta desde 3 m
s
en un tiempo de un segundo hasta 16 m al tiempo de 4,5s
s
a). Diagrama; se presenta en la fig 2.14

166. 154 Movimiento
b). ¿Cual es la velocidad inicial (vo ) del auto?
m
vo = 3
s
c). ¿Cual es la velocidad final (vf ) del auto?
m
vf = 16
s
d). ¿Cual es el tiempo inicial?
ti = 1s
e). ¿Cual es el tiempo final?
tf = 4,5s
f ). ¿Cual es el cambio en la velocidad?
m m m
∆v = vf − vi = 16 −3 = 13
s s s
g). ¿Cual es el cambio en eltiempo?
∆t = tf − ti = 4,5s − 1s = 3,5s
h). ¿Cual es la aceleraci´n del auto?
o
Figura 2.14: Ejemplo 2.1.5.1 del MRUV

167. 2.1 Movimiento en una Dimensi´n
o 155
R. De la relaci´n 2.8
o
vf − vi
a=
tf − ti
16 m − 3 m
s s 13 m
s
m
a= = = 3,71 s
4,5s − 1s 3,5s s
m
a = 3,71 s2 hacia la derecha.
Ejemplo:2.1.5.2 Un ni˜o se mueve con una velocidad inicial de
n
m m
5 s, su aceleraci´n es de 2 s2 Todo esto en tiempo de 3 segundos.
o
a). Diagrama; se presenta en la fig. 2.15
Figura 2.15: Ejemplo 2.1.5.2 MRUV
b). ¿Cual es la velocidad final (vf ) del ni˜o?
n
Por la ec. 2.11
vf = vo + at
m m m ms/ m m m
vf = 5 + 2 2 (3s) = 5 + 6 =5 + 6 = 11
s s s s·/
s s s s
vf = 11 m hacia la derecha
s

168. 156 Movimiento
c). ¿Cual es la distancia que recorre en ese tiempo?
De la ec. 2.14
1
x = vo t + at2
2
sustituyendo:
m 1 m
x= 5 (3s) + 2 2 (3s)2
s 2 s
ms 1
/ m
x = 15 + 2 2 (9s2
ր)
/
s 2 ր s
1
x = 15m + (18m)
2
18
x = 15m + m
2
x = 15m + 9m
x = 24m a la derecha.
Ejemplo: 2.1.5.3 Se lanza una piedra desde una altura de 15 m
partiendo del reposo.
a). Diagrama; se presenta en la fig. 2.16
b). ¿Cual es la velocidad inicial (v0 )?
Puesto que parte del reposo, su velocidad inicial es cero;
vo = 0
c). ¿Cual es su velocidad en un tiempo de 1 s?
En ca´ libre, como se dijo en la secci´n: 2.1.5, la ca´
ıda o ıda
m
libre es un MRUV, con aceleraci´n de -9.81 s2 , por lo que
o
son v´lidas las relaciones dadas en la tabla: 2.3, cambiando
a
x→hya→g

169. 2.1 Movimiento en una Dimensi´n
o 157
Mediante la ec. 2.11
vf = vo + at
cambiando variables
vf = vo + gt
sustituyendo:
m m
vf = 0 + −9,81 2 (1s)
s s
m
vf = −9,81 (1s)
/
s·/s
m
vf = −9,81
s
vf = 9,81 m
s hacia abajo.
d). ¿Cuanto habr´ caido en un tiempo de 1 s?
a
por ; 2.14
1
x = vo t + at2
2
Figura 2.16: Ejemplo 2.1.5.3 MRUV

170. 158 Movimiento
cambiando variables
1
h = vo t + gt2 (2.19)
2
Sustituyendo:
m 1 m
hf = 0 (1s) +
/ −9,81 2 (1s)2
/
s 2 s
1 m
hf = −9,81 2 (1s2
ր)
2 ր
s
1
h = (−9,81m)
2
h = −4,905m
h = 4,905m hacia abajo.
e). ¿Con que velocidad toca el suelo?
por ; 2.18
2 2
vf = vo + 2ax
cambiando variables
2 2
vf = vo + 2gh
Sustituyendo:
2 m
vf = 0 + 2 −9,81 (−15m)
s2
2 m2
vf = 2 147,15 2
s
pero como se busca vf , entonces se debe sacar la raiz cua-
drada a ambos miembros de la igualdad para que no se
altere:
2 = m2
vf 294,3 2
s

171. 2.1 Movimiento en una Dimensi´n
o 159
tomando el valor negativo de la raiz1 , la velocidad con que
toca el suelo es:
vf = −17,16 m
s
Casos de Movimientos Acelerados.
2.1.6. Caida Libre y Tiro Vertical
Uno de los casos es la ca´ libre de los cuerpos, estudiada
ıda
por Galileo Galilei en el siglo XVII, para el cual se ha realizado
el Ejemplo 2.1.5.
Al hablar sobre la ca´ de los cuerpos, Galileo dice: Todos
ıda
sabemos que es subir y lo que es caer, lo que est´ arriba y lo que
a
est´ abajo. Sabemos desde muy peque˜os que lo que sube tiene
a n
que caer.
Si se lanza una piedra hacia arriba, cuando se le acabe el
impulso se parar´ un instante y depu´s caer´ r´pidamente al
a e a a
suelo...
Cuando se suelta una piedra que se tiene en la mano, cae en
l´nea recta hasta el suelo. Si se arroja hacia adelante, se ve que
ı
avanza un poco en l´nea recta, horizontal al suelo, y luego [sic]
ı
comienza a curvarse hacia abajo hasta caer.
Esto mismo ocurre con con la bala cuando se dispara un
ca˜´n, lo cual causa muchos problemas a los artilleros para dar
no
en el blanco.
Lo anterior, describe tres formas de lanzar un proyectil, ver
la figura: 2.17
iniciando con el primer caso:
Tiro Vertical.
El cuerpo parte con una velocidad, sube hasta una altura h,
se detiene un instante y comienza a caer hasta chocar con el
1
Conteste esta pregunta: ¿por qu´ la raiz negativa?. Explique sus razones.
e

172. 160 Movimiento
suelo. Generalmente se busca la altura a la que llega el proyectil
lanzado, el tiempo que tarda en subir y bajar y la velocidad que
Figura 2.17: Formas de Lanzar un Proyectil
Figura 2.18: Tiro Vertical de un Proyectil, (la l´
ınea punteada del color del
proyectil indica la trayectoria de bajada.)

173. 2.1 Movimiento en una Dimensi´n
o 161
adquiere en alg´n instante, por esto, se tratar´n estos casos.
u a
Altura M´xima Alcanzada
a
Para este caso se da la velocidad inicial vo , entonces por 2.18
2 2
vf = vo + 2ax
cambiando variables
2 2
vf = vo + 2gy
pero vf = 0,
2
0 = vo + 2gy
v2
⇒y=− o (2.20)
2g
Tiempo que tarda en subir
El tiempo que tarda en subir, se puede encontrar por medio
de la ec2.11
vf = vo + at
cambiando variables:
vf = vo + gt
aqu´ puesto que vf = 0;
ı
0 = vo + gt
vo
⇒ ts = − (2.21)
g
el tiempo que tarda en llegar al lugar donde parti´ es igual al
o
de subida, por lo que tarda en el vuelo: 2ts a lo que se le llama
tiempo de vuelo (tv ).
vo
⇒ tv = −2 (2.22)
g

174. 162 Movimiento
Ejemplo: 2.1.6. Se lanza una pelota en forma vertical hacia arri-
ba con una velocidad de 3 m .
s
a). Diagrama; se presenta en la fig. 2.19
Figura 2.19: Ejemplo 2.1.6 Tiro Vertical
b). ¿Cual es la velocidad inicial (v0 )?
Su velocidad inicial es; vo = 3 m
s
c). ¿Cual es su velocidad en un tiempo de 0,3 s?
Mediante la ec. 2.11
vf = vo + at
cambiando variables
vf = vo + gt
sustituyendo:
m m
vf = 3 + −9,81 (0,3s)
/
s s·/
s

175. 2.1 Movimiento en una Dimensi´n
o 163
m m m
vf = 3 − 2,943 = 0,0057
s s s
vf = 0,0057 m
s hacia arriba, la velocidad disminuy´ (casi es
o
cero).
c). ¿Cual es su velocidad en un tiempo de 1 s?
Mediante la ec. 2.11
vf = vo + at
cambiando variables
vf = vo + gt
sustituyendo:
m m
vf = 3 + −9,81 (1s)
/
s s·/
s
m m m
vf = 3 − 9,81 = −6,81
s s s
m
vf = 6,81 s hacia abajo, es decir que ha pasado del lugar
de donde parti´.
o
d). ¿Cuanto tiempo tarda en subir?.
Por 2.21:
vo 3m
s
ts = − = − m
g −9,81 s2
m
ր
s
ts = 0,306 m = 0,306s
ր
s·s
e). ¿Cuanto tiempo esta en vuelo?.
tv = 2ts = 2(0,306s) = 0,612s

176. 164 Movimiento
f ). ¿que altura alcanza?.
Por 2.20:
2
vo (3 m )2
s
y=− =− m
2g 2(−9,81 s2 )
9 ( m )2
s ( m·m
ր)
s2
y= m = 0,459 m
19,62 s2 ր
s2
ha subido: = 0,459m
Ejemplo: 2.1.6. Se lanza una pelota en forma vertical hacia arri-
ba con una velocidad de 30 m/s, Encuentre: El tiempo de subida,
el tiempo de vuelo, la altura m´xima alcanzada y la distancia
a
total recorrida.
a). ¿Cual es la velocidad inicial (v0 )?
Su velocidad inicial es; vo = 30 m
s
b). ¿Cuanto tiempo tarda en subir?.
Por 2.21:
vo 30 m
s
ts = − = − m
g −9,81 s2
m
ր
s
ts = 3,06 m = 3,06s
ր
ր·s
s
c). ¿Cuanto tiempo esta en vuelo?.
tv = 2ts = 2(3,06s) = 6,12s
d). La altura m´xima alcanzada es.
a
Por 2.20:
2
vo (30 m )2
s
y=− =− m
2g 2(−9,81 s2 )

177. 2.1 Movimiento en una Dimensi´n
o 165
900 ( m )2
s ( m·m
ր)
s2
y=− m = 45,87 m
19,62 s2 ր
s2
ha subido: = 45,87m
e). La distancia total recorrida es la distancia que sube y la que
baja por lo que es:
2(altura subida)=2(45.87 m)=91.74 m
Pr´ctica 3.
a
Movimiento Rectilineo Uniforme Acelerado
Objetivo. Observaci´n de un Movimiento Rectil´
o ıneo Uniforme
Acelerado.
Aplicaci´n de los conceptos aprendidos sobre este subtema.
o
Mediante el uso de materiales de uso com´n, observar el Mo-
u
vimiento Rectil´
ıneo Uniforme Acelerado.
Medici´n de distancia y tiempo aplicando las ecuaciones co-
o
nocidas, as´ como, la teor´ de errores para la expresi´n de los
ı ıa o
resultados y mediciones.
Introducci´n
o
Existen varias maneras de poder observar este tipo de movi-
miento, el mas sencillo es la caida libre, la dificultad es a me-
dici´ndel tiempo, sin embargo actualmente existen los tel´fonos
o e
celulares que tienen la capacidad de fotografiar, o filmar, la caida
libre.
Una variaci´n de este m´todo lo invent´ Galileo, consiste en
o e o
retardar el movimiento de caida libre. Esto se consigue realizan-
do una rampa por la cual se deslice un bal´ o canica. El canal
ın
puede ser:

178. 166 Movimiento
Un tubo transparente.
Dos tubos de luz fluorescente de dos o tres metros unidos con
cinta adhesiva.
Una rampa de laboratorio exprofeso para esta pr´ctica.
a
En esta pr´ctica, el equipo decidir´ que material a utilizar.
a a
Construcci´n del instrumento.
o
Conf´rmense en equipos de hasta 5 elementos, nombrando un
o
representante.
Decidan que tipo de material usar´n.
a
Realice una descripci´n de la construcci´n del prototipo.
o o
De ser posible Como camara fotogr´fica y cron´metro utilice
a o
un celular.
Dibuje o fotograf´ los pasos realizados.
ıe
Experimento.
Descripci´n del Procedimiento.
o Medir el tiempo que tarda en
pasar los pimeros 10 cm, o 20 cm seg´n sea el caso, cuidando
u
de que el cron´metro inicie cuando pase por el inicio del movi-
o
miento.
realice este procedimiento por lo menos cinco veces.
Dibuje o fotograf´ los pasos realizados.
ıe

179. 2.1 Movimiento en una Dimensi´n
o 167
Indicaciones para el Reporte.
1. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
2. Se entregar´ un reporte por equipo.
a
3. El reporte de la pr´ctica debe contener:
a
* Presentaci´n. o
* Introducci´n. o
* Desarrollo.
* Conclusiones.
* Bibliograf´ ıa.
4. Discuta en equipo el contenido de cada uno de los puntos
que debe contener el reporte
5. Para el paso llamado desarrollo, tomar como base en la
pr´ctica realizada:
a
6. Reunirse en equipo la obtenci´n del material y la construc-
o
ci´n del prototipo.
o
7. Anotar la descripci´n de los pasos numer´ndolos, por ejem-
o a
plo:
1.- Construcci´n. o
2.- Desarrollo
3.-
4.- . . . . . .
5.- Realizar un cuadro donde se presenten las mediciones y
c´lculos realizados.
a
6.- como son cinco integrantes deben reportarse cinco me-
diciones.
7.- Discuta en equipo el contenido de las conclusiones y la
bibliograf´ ıa.

180. 168 Movimiento
Para la evaluaci´n de la Pr´ctica 2 se tomar´ en cuenta:
o a a
1. Entrega en tiempo y forma (Una semana m´ximo).
a
2. Validez y pertinencia de las ideas expuestas.
3. Profundidad de los conceptos.
4. Revisi´n del contenido.
o
5. Presentaci´n al profesor del prototipo por el coordinador.
o
6. Habra una coevaluaci´n por lo que se debe poner de acuerdo
o
con el profesor.
7. La evaluaci´n se reportar´ en un cuadro como el siguiente:
o a
Indicador si no ponder. calif.
Present´ en tiempo y forma
o 1
Present´ el prototipo
o 1
El reporte contiene:
Introducci´n
o 1
Desarrollo 2
Conclusiones 1
Bibliograf´
ıa 1
Existe Validez y pertinencia 1
de las ideas expuestas
Existe Claridad y coherencia 1
en el escrito.
Existe Profundidad en los 1
conceptos
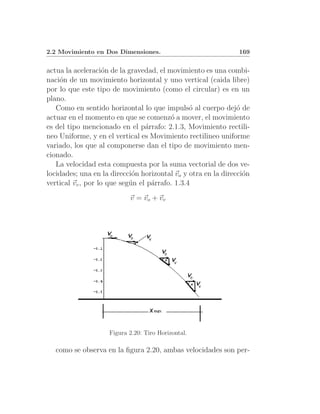
2.2. Movimiento en Dos Dimensiones.
2.2.1. Tiro Parab´lico Horizontal y Oblicuo.
o
Como dice Galileo:
Si [...] arrojamos [una piedra] hacia adelante, vemos que avan-
za un poco en l´ ınea recta, horizontal al suelo, y luego [sic] co-
mienza a curvarse hacia abajo hasta caer, realmente, su trayec-
toria es curva inmediatamente que se comienza a mover, ya que

181. 2.2 Movimiento en Dos Dimensiones. 169
actua la aceleraci´n de la gravedad, el movimiento es una combi-
o
naci´n de un movimiento horizontal y uno vertical (caida libre)
o
por lo que este tipo de movimiento (como el circular) es en un
plano.
Como en sentido horizontal lo que impuls´ al cuerpo dej´ de
o o
actuar en el momento en que se comenz´ a mover, el movimiento
o
es del tipo mencionado en el p´rrafo: 2.1.3, Movimiento rectili-
a
neo Uniforme, y en el vertical es Movimiento rectilineo uniforme
variado, los que al componerse dan el tipo de movimiento men-
cionado.
La velocidad esta compuesta por la suma vectorial de dos ve-
locidades; una en la direcci´n horizontal vo y otra en la direcci´n
o o
vertical vv , por lo que seg´n el p´rrafo. 1.3.4
u a
v = vo + vv
Figura 2.20: Tiro Horizontal.
como se observa en la figura 2.20, ambas velocidades son per-

182. 170 Movimiento
pendiculares (forman 90o entre ellos), por lo que se puede realizar
un an´lisis en las dos dimensiones.
a
En sentido horizontal,
xmax
voh = (2.23)
tc
donde voh = velocidad inicial en sentido horizontal, la que
adem´s no cambia porque es MRU
a
xmax = distancia m´xima recorrida o alcance,
a
tc = tiempo de caida, de:
1
y = vov t + gt2
2
puesto que en sentido vertical es caida libre e inicia del reposo,
vov = 0:
1 2y
y = gt2 ⇒ t2 =
2 g
sacando la raiz cuadrada:
2y
t=
g
si y = hc ⇒ t = tc :
2hmax
tc = (2.24)
g
entonces el alcance es:

183. 2.2 Movimiento en Dos Dimensiones. 171
xmax = voh tc (2.25)
En sentido vertical, por la ec. 2.11,
vf v = vov + at
puesto que es caida libre e inicia del reposo, vov = 0 y a = g,
entonces:
vf v = gt (2.26)
la velocidad con la que toca el suelo es:
vf v = gtc (2.27)
el ´ngulo que forman las velocidades en cualquier instante es:
a
vf v
tan θ =
voh
sustituyendo 2.26
g
tan θ = t (2.28)
voh

184. 172 Movimiento
Ejemplo: 2.2.1. Desde un avi´n se lanza una bomba a una al-
o
tura de 3000 m; si la velocidad que lleva el avi´n es de 648 km .
o hr
a). ¿Cual es la velocidad inicial (voh )?
Su velocidad inicial es; voh = 648 km = 180 m
hr s
b). ¿Cuanto tiempo tarda la bomba en llegar a la tierra?.
Por 2.24:
2hmax
tc =
g
2(−3000m ւ)
tc =
−9,81 m
ւ
s2
6000
tc =
9,81 s12
tc = 24,73s
c). La distancia horizontal m´xima alcanzada es.
a
Por 2.25:
xmax = voh tc
sustituyendo
m
xmax = 180 (24,73s)
/
/
s
Cae a una distancia de: = 4446.m del sitio donde se lanz´.
o

185. 2.2 Movimiento en Dos Dimensiones. 173
Figura 2.21: Figura para el problema 2.2.1.
Movimiento Parab´lico.
o
Es el movimiento realizado por un proyectil disparado con
una velocidad inicial (vo ) a un ´ngulo (θ), este movimiento es
a
compuesto porque en el interaccionan un MRU (en sentido hori-
zontal) y un MRUV (en sentido vertical), por esto constituye un
movimiento en un plano. La componente horizontal vx es cons-
tante puesto que una vez lanzado el proyectil, no act´a ninguna
u
fuerza, por lo que es MRU.
vx = voh = vo cos θ (2.29)
en sentido vertical por la relaci´n 2.11
o
vf = vo + at
vf = vy = voy + gt
pero para este caso: voy = vo sin θ por lo que se tiene:

186. 174 Movimiento
vov = vo sin θ + gt (2.30)
la velocidad resultante seg´n la relaci´n: 1.8es:
u o
v = vx + vy
el angulo que forma esta velocidad con el eje horizontal es me-
diante la relaci´n 1.11
o
vy
θ = tan−1
vx
Figura 2.22: Gr´fica del Movimiento Parab´lico, mostrando las velocidades
a o
en varios puntos.

187. 2.2 Movimiento en Dos Dimensiones. 175
relaci´n de la Trayectoria
o
mediante la ec 2.23:
x
vo cos θ =
t
x
=⇒ t =
(vo cos θo )
la ordenada es por 2.19:
1
y = vo t + gt2
2
sustituyendo el tiempo (t):
2
(vo sin θo ) 1 x
y= x+ g
(vo cos θo ) 2 (vo cos θ)
(vo sin θo ) g 2
y= x+ 2x (2.31)
(vo cos θo ) 2 (vo cos θ)
la que corresponde a la relaci´n de una par´bola.
o a
Tiempo de vuelo
De la figura: 2.22, se puede ver que cuando alcanza la m´xima
a
altura, ha recorrido la mitad del tiempo de vuelo o en otras
palabras el tiempo que tarda en subir. Por otra parte, en ese
punto, la velocidad en sentido vertical es cero. Por lo que:
0 = (vo sin θo ) + gts

188. 176 Movimiento
(vo sin θo )
=⇒ ts = −
g
pero lo que tarda en subir es igual a lo que tarda en caer, por lo
que el tiempo de vuelo es:
(2vo sin θo )
tv = 2ts = − (2.32)
g
Altura M´xima (hmax ).
a
Obsevando de nueva cuenta la figura: 2.22, en el punto donde
se alcanza la altura m´xima la componente de la velocidad en
a
sentido vertical es cero (vy = 0), por lo que de la misma forma
que en la subsecci´n 2.1.6, relaci´n 2.20, con la particularidad
o o
que vo toma el valor de vo sin θ por ser ´sta la componente en
e
sentido vertical para el tiro parab´lico.
o
(vo sin θ)2
hmax = −
2g
Alcance (Rango).
Por la relaci´n 2.25
o
xmax = voh tv (2.33)
pero voh = vo cos θ y el tiempo de vuelo (tv ) por la relaci´n
o
2.32 es
(2vo sin θo )
tv = −
g

189. 2.2 Movimiento en Dos Dimensiones. 177
sustituyendo en 2.33
(2vo sin θo )
R = (vo cos θo ) −
g
utilizando las propiedades de la igualdad, se puede escribir:
2 2 sin θo cos θo )
R = −vo
g
pero por la identidad trigonom´trica: sin(2θ) = 2 sin θ cos θ, se
e
puede escribir:
2
vo
R=− sin(2θo ) (2.34)
g
´
Figura 2.23: Envolvente de las Trayectorias Cuyo Angulo de Disparo est´ En-
a
o
tre 0 y 180 (Par´bola de Seguridad)
a

190. 178 Movimiento
Ejemplo: 2.2.1
Se lanza una bala mediante un ca˜´n con un ´nguo de 65o .
no a
a). Dibujo de la trayectoria fig 2.24
b). ¿Cual es la componente horizontal de la velocidad inicial
(voh ) de la bala?. Por 2.29
voh = vo cos θ
m
voh = 50 cos 65o
s
m
voh = 50 (0,42261826)
s
m
voh = 21,13
s
c). ¿Cual es la componente vertical de la velocidad inicial (vov )
de la bala?. Por 2.30
vov = vo sin θ + gt
Figura 2.24: Ejemplo 2.2.1 Tiro Parab´lico.
o

191. 2.2 Movimiento en Dos Dimensiones. 179
pero t = 0 por ser el inicio del vuelo:
m
vov = 50 sin 65o
s
m
voh = 50 (0,906308)
s
m
voh = 45,31
s
d). ¿Que altura m´xima alcanza? por 2.34
a
(vov sin θo )2
hmax =−
2g
2
50 m sin(65o )
s
hmax =− m
2(−9,81 s2 )
pero 50 m sin(65o ) = 45,31 m ya que se calcul´ en el inciso
s s o
b)
2
45,31 m
s
hmax = − m
(−19,62 s2 )
2052,9961 m·m
ւs2
/
hmax = − m
/
(−19,62ւ )
s2
R. La altura que alcanza es 104,64m.
e). ¿Cual es el alcance?
usando la ec. 2.34
2
vo
R=− sin(2θo )
g
2
50 m
s o
R=− m sin(2(65 ))
−9,81 s2

192. 180 Movimiento
2500 m·m
ւs2
/
R= m
/
sin(130o )
9,81ւ
s2
R = 254,84m(0,766044)
El alcance R es : 195,22m
e). ¿Cual es el tiempo de vuelo?
por 2.32
(2vo sin θo )
tv = −
g
2 50 m sin(65o )
s
tv = − m
−9,81 s2
(100ւ )(0,906307)
m
ւ
s
tv = m
ւ
9,81 s·s
ւ
El tiempo de vuelo es: 9,24s
e). ¿Cual es la velocidad resultante a lo 3 segundos despu´s de
e
que se dispara la bala?
por 1.8
v = vx + vy
ahora bien, ya que vx = voh = 21,13 m y por 2.30
s
vv = vo sin θ + gt
m m
vv = 50 sin(65o ) + −9,81 2 (3s)
s s
m m
vv = 50 (0,906308) − 29,43
s s
m m
vv = 45,31 − 29,43
s s

193. 2.2 Movimiento en Dos Dimensiones. 181
m
vv = 15,88 hacia arriba
s
entonces la velocidad resultante es:
vr = 2 2
vx + vv
m 2 m 2
vr = 21,13 + 15,88
s s
m2
vr = 698,65 2
s
la velocidad resultante para el tiempo de tres segundos es:
vr = 26,43 m
s
f ). ¿que ´ngulo forma con el eje horizontal?
a
por la ec. 1.11
vy
θ = tan−1
vx
−1 15,88 m
s
θ = tan m
21,13 s
θ = tan−1 (0,751538)
′ ′′
El ´ngulo es: 36o 55 34
a
Problemas
1. Un avi´n en vuelo horizontal a una altura de 300 m y con
o
una velocidad de 60 m , deja caer una bomba. Calcular el
s
tiempo que tarda en llegar al suelo, y el desplazamiento
horizontal de la bomba.
2. Se lanza un cuerpo desde el origen con velocidad horizontal
de 40 m , y con una velocidad vertical hacia arriba de 60 m .
s s
Calcular la m´xima altura y el alcance horizontal.
a

194. 182 Movimiento
3. Resolver el ejercicio anterior, tomando como lugar de lan-
zamiento la cima de una colina de 50 m de altura.
4. Se lanza un proyectil desde una colina de 300 m de altura,
con una velocidad horizontal de 50 m/s, y una velocidad
vertical de -10 m/s (hacia abajo). Calcular el alcance hori-
zontal y la velocidad con que llega al suelo.
5. Un ca˜´n dispara una bala desde lo alto de un acantilado
no
de 200 m de altura con una velocidad de 46 m haciendo un
s
o
´ngulo de 30 por encima de la horizontal. Calcular el al-
a
cance, el tiempo de vuelo, y las componentes de la velocidad
de la bala al nivel del mar. Hallar tambi´n la altura m´xi-
e a
ma. (Hallar primero, las componentes horizontal y vertical
de la velocidad inicial).
2.2.2. Movimiento Circular.
Para este movimiento, la trayectoria es un c´ ırculo. Lo que
se desplaza el cuerpo puede ser caracterizado por la medida de
la trayectoria (s) o por el desplazamiento angular, lo ultimo se
´
realiza comunmente.
La unidad de medida utilizada para los ´ngulos es en este
a
caso el radian (rad), este valor se define como: El cociente entre
el el arco de c´
ırculo (s) recorrido y el radio del c´
ırculo.
s
θ= (2.35)
r
cuando lo que se recorre es una vuelta completa, la distancia
recorrida es igual al per´
ımetro del c´
ırculo por lo que:s = 2πr,
entonces:

195. 2.2 Movimiento en Dos Dimensiones. 183
Figura 2.25: Gr´fica del Movimiento Circular
a

196. 184 Movimiento
2πr
θ= (2.36)
r
por lo que una vuelta completa es igual a:
2π[rad]
puesto que lo que ha recorrido se mide en metros y el radio
tambi´n, al realizar el cociente ente s y r, ya no quedan unida-
e
des y por lo tanto, el radian es una cantidad sin dimensiones,
adimensional o n´mero puro.
u
Movimiento Circular Uniforme (MCU).
Cuando un cuerpo se mueve en forma de c´ ırculo,
recorriendo angulos iguales en tiempos iguales.
El movimiento es circular porque es la forma que tiene la tra-
yectoria y uniforme porque tarda el mismo intervalo de tiempo
en recorrer el ´ngulo, este caso es an´logo al MRU, las carac-
a a
ter´
ıstiacs que presenta son:
Periodo (T ). El tiempo que tarda en dar una vuelta completa
alrededor de un centro.
Frecuencia (f ´ ν). es el n´mero de vueltas que da un cuerpo
o u
en un tiempo (t).
´
Desplazamiento Angular: Angulo sobre el que se mueve la
part´
ıcula o el radio vector.

197. 2.2 Movimiento en Dos Dimensiones. 185
Velocidad Lineal (v). Vector tangente a la trayectoria per-
pendicular al radio vector.
Figura 2.26: Velocidad Lineal(v)
Analizando las definiciones de Periodo (T ) y frecuencia (f ), se
llega a la conclusion que son inversas por lo que se dice que:
1
f= (2.37)
T
como el Periodo (T) se mide en segundos [s], entonces la
frecuencia se medir´ en 1 , unidad a la que se le llama Hertzio
ıa s
o Hertz [Hz] en honor al f´ ısico Estadounidense Hernry Hertz
quien fue el primero en detectar las Ondas Electro-Magn´ticas.
e
1
f [=] [=]s−1 [=]Hz.
s
En algunos textos, la frecuencia se representa por medio de la
letra griega “nu” (ν)

198. 186 Movimiento
Velocidad Angular.
Se define como:
El cambio en el desplazamiento angular (radia-
nes) didvidido por el cambio en el tiempo (segun-
dos), se designa por medio de la letra griega omega
min´scula (ω)
u
∆θ
ω= (2.38)
∆t
θf − θi
ω= (2.39)
tf − ti
por lo que la velocidad angular ω se mide en
rad
s
Velocidad Lineal
Por la definici´n de velocidad, se tiene;
o
∆d sf − si
v= = (2.40)
∆t tf − ti

199. 2.2 Movimiento en Dos Dimensiones. 187
despejando s de la relaci´n (2.35),
o
s = θr
de la figura 2.26, se puede observar que a cada s, le corresponde
una velocidad lineal, por lo que;
θf r − θi r
v=
tf − ti
factorizando r, se tiene:
θ f − θi
v= r (2.41)
tf − ti
pero por (2.39),
v = ωr (2.42)
Ejercicios
Un cuerpo atado a una cuerda de 1 metro, gira 50 vueltas en
un tiempo de un minuto.
a). Haga un diagrama que describa el problema.
b). ¿Cuantas vueltas da?
R: 50 vueltas
c). ¿En que tiempo medido en segundos gira?
R: 60 s

200. 188 Movimiento
Figura 2.27: Diagrama para el ejercicio 2.2.2

201. 2.2 Movimiento en Dos Dimensiones. 189
d). ¿Cuantas revoluciones por minuto da?
1 revoluci´n = 1 vuelta
o
rev. por min.= 50 min
1
rev.
e). ¿Cuantas revoluciones por segundo da?
rev. por seg.= 60 rev. = 6 rev.
50
s
5
s
rev. por seg.= 0.83 rev.s
f ). ¿Cual es su Velocidad angular (ω)?
por cada vuelta el desplazamiento angular es
θ = 2π[rad] pero como da 50 vueltas: ⇒ θ = 2(50)π[rad] =
100π [rad]
100π[rad]
ω=
60[s]
10 rad
ω= π
6 s
rad
ω = 5,24
s
g). ¿Cual es su Frecuencia (f )?
da 50 vueltas en un minuto, entonces:
50 vueltas 5 1
f= =
60 s 6 s
f = 0,83 [Hz]
h). ¿Cual es su periodo (T )?
1 1
T = =
f 0,83 [Hz]
1
T = 1,20 1
s

202. 190 Movimiento
T = 1,20 s
i). ¿Cual es su velocidad lineal (v)?
mediante la relaci´n: (2.42)
o
v = ωr
rad
v= 5,23 (1[m])
s
m
v = 5,23
s
Acelaraci´n Centr´
o ıpeta.
En el Movimiento Circular uniforme, la velocidad lineal es la
misma siempre, pero cambia de direcci´n constantemente, como
o
se puede ver en la figura 2.26, puesto que la aceleraci´n es el
o
cambio en la velocidad en el cambio en el tiempo, en este caso
se tiene una aceleraci´n como resultado de esta situaci´n.
o o
Actividad: Tarea

203. 2.2 Movimiento en Dos Dimensiones. 191
Actividad. 2.2.2 Para determinar su valor, se realizar´ el si-
a
guiente procedimiento:
Paso 1. Trazar un c´ ırculo de 10 cm de radio.
Paso 2. Delimitar mediante dos radios un arco de c´ ırculo (s) de 10
cm. Se construy´ as´ un radi´n.
o ı a
Paso 3. En cada extremo del arco, trazar l´ ıneas perpendiculares a
los radios iguales a 10 cm.
Paso 4. Encontrar el punto medio del ´ngulo y trazar por este punto
a
un radio del c´ ırculo.
Paso 5. Leer nuevamente la secci´n 1.3.4, para recordar como se en-
o
cuentra la dferencia de vectores.
Paso 6. Consultar la secci´n 2.1.4 para recordar como se puede en-
o
contrar la aceleraci´n.
o
Paso 7. Contestar las siguientes preguntas:
Pregunta 1. Hacia donde esta dirigido el vector cambio en la veloci-
dad (∆v).
Pregunta 2. Los tri´ngulos que se dibujaron ¿se parecen?, es decir
a
¿son semejantes?
Pregunta 3. ¿Que dice la geometr´ sobre la semejanza de tri´ngu-
ıa a
los?
Aprovechando la semejanza de tri´ngulos, se puede admitir
a
que:
∆v s s
= ⇒ ∆v = v
v r r
aprovechando la propiedad de la igualdad que dice que al dividir
los dos miembros de la igualdad por un valor ´sta no se altera,
e
entonces dividiendo ambos miembros por el cambio en el tiempo
(∆t), se tiene
∆v s v s
=v =
∆t r(∆t) r ∆t
se observa que el primer miembro de esta igualdad es la acele-
s
raci´n y que el cociente ∆t , es la velocidad. Entonces: El Movi-
o
miento Circular Uniforme (MCU)

204. 192 Movimiento
Figura 2.28: Aceleraci´n Centr´
o ıpeta

205. 2.2 Movimiento en Dos Dimensiones. 193
Propiedad 1. Aun cuando su velocidad lineal no cambia,
produce una aceleraci´n.
o
Propiedad 2. La acleraci´n se encuentra dirigida hacia el
o
centro. Por lo que se le llama Centr´
ıpeta.
Su valor se encuentra mediante la expresi´n:
o
vv v2
ac = = (2.43)
r r
¿En que se mide?
2
( m )2
s ( m2 ) m · m
/
ac [=] = s = m
m 1 m2
/s
m
ac [=] 2
s
Ahora bien recordando que v = ωr, sustituyendo en (2.43), se
tiene
ω 2r2
ac =
r
ac = ω 2 r (2.44)
Donde:
m
ac = Aceleraci´n Centr´
o ıpeta s2
m
v = Velocidad Lineal o Tangencial s
ω = Velocidad angular rad s
r radio de la trayectoria m

206. 194 Movimiento
Ejercicios
¿Que aceleraci´n tiene un movil que viaja sobre una circun-
o
ferencia de 12 m de radio con una velocidad tangencial de 6 m ?
s
a). Haga un diagrama que describa el problema.
Figura 2.29: Diagrama para el ejercicio 2.2.2
b). ¿Que velocidad lineal lleva?
R: 6 m
s
c). ¿Cual es el radio de la trayectoria?
R: 12 m
d). ¿Cual es su aceleraci´n centr´
o ıpeta?
mediante la expresi´n (2.43)
o

207. 2.2 Movimiento en Dos Dimensiones. 195
v2 (6 m )2
ac = = s
r 12m
2
(36 m2 )
s
ac =
12m
m
ac = 3 2
s
Movimiento Circular Uniforme Variado (MCUA).
As´ como existe un Moviento Rectilineo Uniforme Variado
ı
(MUA), tambi´n existe un Movimiento Circular Uniforme Va-
e
riado, ya que la velocidad angular puede cambiar a consecuencia
de una Fuerza que aumente la aceleraci´n angular.
o
La aceleraci´n angular es el cambio en la velocidad angular
o
dividida por el cambio en el tiempo, dada por:
ωf − ωi ∆ω
α= = (2.45)
tf − ti ∆t
donde:
rad
∆ω = Cambio en la Velocidad angular s
∆t = Cambio en el tiempo [s]
α = aceleraci´n angular rad
o s2
Las ecuaciones del movimiento Circular Uniforme Variado
(MCUA) son semejantes a las del MUA, por lo que se ponen en
este lugar, dando, de paso, tambi´n un ejemplo de las simetr´
e ıas
(semejanzas) que existen en la f´
ısica.

208. 196 Movimiento
Ejemplo 2.2.2 La velocidad angular de un motor es de 900 rpm,
y desciende de manera uniforme hasta 300 rpm, en 2.5 segundos.
a) ¿Cual es su velocidad angular inicial?
rev
ր rad 1min
ւ rad
ω0 = 900 2π = 30π
min
ւ rev
ր 60s s
b) ¿Cual es su velocidad angular final?
rev
ր rad 1min
ւ rad
ωf = 300 2π = 10π
min
ւ rev
ր 60s s
c) ¿Cual es el cambio en la velocidad angular?
rad rad rad
∆ω = 10π − 30π = −20π
s s s
d) ¿Cual es la aceleraci´n angular?
o
vo+vf ωo+ωf
v = 2 ω = 2
vo+vf ωo+ωf
x = 2 t θ = 2 t
vf = vo + at ωf = ωo + αt
x = vot + 2 at2 θ = ωot + 1 αt2
1
2
2 2 2 2
vf = vo + 2ax ωf = ωo + 2αθ
Cuadro 2.4: Ecuaciones del MCUV ´ MCUA
o

209. 2.2 Movimiento en Dos Dimensiones. 197
−20π rad
s
α=
2,5s
rad
α = −8π
s2
Ejercicios
1. ¿Que aceleraci´n angular tiene una rueda de 80cm de di´me-
o a
m
tro que gira desde 0 s hasta 1800rpm en 40s?
a). Haga un diagrama que describa el problema.
Figura 2.30: Diagrama para el ejercicio 1
b). ¿Que velocidad lineal alcanza?

210. 198 Movimiento
c). ¿Cual es el radio de la trayectoria?
d). ¿Cual es su aceleraci´n centr´
o ıpeta?
e). ¿Cual es su aceleraci´n angular?
o
2. Una m´quina gira de 800rpm hasta 600rpm dando 100 vuel-
a
tas.
a). Haga un diagrama que describa el problema.
Figura 2.31: Diagrama para el ejercicio 2
b). ¿Cual es su aceleraci´n angular?
o
c). ¿En que tiempo efect´a las 100 vueltas?
u

211. 2.2 Movimiento en Dos Dimensiones. 199
d). ¿Cual es su aceleraci´n centr´
o ıpeta?

212. 200 Movimiento

213. Leyes de Newton, Trabajo,
Potencia y Energ´
ıa.
“El cambio en el movimiento es
proporcional a la fuerza impresa, y
se efect´a en la misma l`nea recta
u ı
en la que se aplica la fuerza.”
ISAAC NEWTON
Segunda Ley

214. 202 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Introducci´n
o
Como la mec´nica fue la primera teor´
a ıa
de la f´ısica en desarrollarse, sirvi´ co-
o
mo modelo para los trabajos futuros, en
alg´n momento existi´ el deseo y la ilu-
u o
si´n de reducir toda la f´
o ısica a la mec´ni-
a
ca (la unificaci´n es una idea sencilla y
o
atractiva que siempre se va a encontrar
a lo largo de la historia).
Issac Newton. El siglo XVII result´ ser una mala ´poca pa-
o e
ra Inglaterra. A los a˜os de revoluci´n, guerra civil, dictadura,
n o
restauraci´n, d´
o ısputa religiosa, desorden general, muertes y ca-
lamidades que asolaron el pa´ a mediados del siglo, sigui´ una
ıs o
plaga de peste bub´nica que, caus´ m´s de 68,000 muertes.
o o a
En el verano de 1665, menciona un documento de la ´poca, e
placi´ a Dios Todopoderoso en su justa severidad que visitase
o
esta villa de Cambridge la plaga de la pestilencia. Se dispuso ce-
rrar los colegios de la universidad y dispersar a sus estudiantes
por el pa´ El Trinity College lo hizo el 7 de agosto. Entre los
ıs.
alumnos se hallaba un muchacho “sobrio, silencioso y pensativo”
llamado Isaac Newton. El joven estudiante abandon´ Cambridge
o
y se dirigi´ a su casa materna de Woolsthorpe, en el condado de
o
Lincolnshire, donde hab´ nacido 23 a˜os antes. All´ pasar´ cer-
ıa n ı ıa
ca de dos a˜os. En un pasaje autobiogr´fico, el propio Newton
n a
relataba cincuenta a˜os m´s tarde, que en ese bienio hab´ halla-
n a ıa
do el m´todo de las series aproximadas para reducir la dignidad
e
(potencia) de un binomio; el m´todo de tangentes; la teor´ de
e ıa
los colores. . .

215. Din`mica
a 203
Anni mirabilis (a˜os maravillosos) se ha llamado a ese bie-
n
nio 1665 − 1666, puesto que al parecer, en su transcurso Isaac
Newton ide´ todo lo que le debe la ciencia. Por aquel entonces,
o
contaba con 24 a˜os de edad.
n
Ten´ una man´ sumamente util: apuntarlo todo en cuader-
ıa, ıa ´
nitos. Conocido es el de sus pecados, en el que hac´ constar
ıa
cosas como impertinencia con mi madre; peg´ndole a mi her-
a
mana; robando cerezas a Eduard Storer; haciendo una ratonera
en tu d´ Se˜or, y otros pecadillos por el estilo, sin embargo,
ıa, n
llen´ otros cuadernos con notas y diagramas cient´
o ıficos precisos.
En su obra ((Principia)) (1687), aplica por igual su nueva ley
de gravedad a los arcos descritos por las balas de ca˜´n, a las
no
´rbitas de los sat´lites y planetas y a las trayectorias de los
o e
cometas, calculando sus posibles rutas en forma detallada. Era
tambi´n un hombre de fe religiosa. Es as´ que, en las mismas
e ı
Principia, Newton describe al espacio a semejanza al cuerpo
de Dios: “El Dios Supremo es un Ser eterno, infinito, absolu-
tamente perfecto. . . Perdura eternamente y es omnipresente; y
esta existencia eterna y omniprescencia constituyen la duraci´n o
y el espacio”. Igualmente, Newton sostiene que “este bell´ ısimo
sistema de Sol, planetas y cometas s´lo podr´ provenir de la
o ıa
sabidur´ y dominio de un Ser poderoso e inteligente”. As´ para
ıa ı,
Newton, el universo considerado como un todo, era est´tico.
a
Pensaba que el universo no pod´ estar expandi´ndose o con-
ıa e
tray´ndose globalmente puesto que tales movimientos requieren
e
por necesidad de un centro, tal como una explosi´n tiene su cen-
o
tro y la materia esparcida en un espacio infinito no define ning´n
u
centro. Esta situaci´n es erronea, puesto que se ha demostrado
o
que el universo se expande. En consecuencia, estudiando los he-
chos hacia el pasado, el cosmos deber´ ser est´tico; o sea, que
ıa a

216. 204 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
termin´ sustentando la tradici´n aristot´lica de un cosmos sin al-
o o e
teraci´n. A fin de cuentas, el legado de Arist´teles termin´ hasta
o o o
fines de la d´cada de 1920, ya que s´lo entonces, esa tradici´n, se
e o o
empez´ a cuestionar debido a la teor´ general de la relatividad
o ıa
y a las evidencias observacionales.
Existe algo unico en el hecho de que Isaac Newton, todo un
´
profesor del Trinity College (Colegio de la Trinidad), fuera un
Unitario, es decir que sab´ que Jes´s no forma parte de la Tri-
ıa u
nidad.
Isaac Newton muri´ un 20 de marzo de 1727, y fue enterrado
o
con todos los honores en la abad´ de Westminster junto a los
ıa
grandes hombres de la historia inglesa. Su epitafio dice: ¡ Mor-
tales, congratulaos de que un hombre tan grande haya existido
para honra de la raza humana !. El legado cient´ ıfico de Isaac
Newton radica en el hecho de que fu´ el primero que brinda
e
una teor´ unificada y racional del universo: las mismas leyes
ıa
que rigen el movimiento de los astros, rigen tambi´n el de los
e
modestos objetos que nos rodean en la Tierra y todas pueden
expresarse a trav´s de las matem´ticas.
e a
El poeta Alexander Pope, quien vivi´ en tiempos de Newton,
o
escribi´:
o
La Naturaleza y sus leyes yac´ escondidas en la noche
ıan
Dios dijo: “¡Hagamos existir a Newton!”
y se hizo la luz.

217. 3.1 Leyes de Newton. 205
3.1. Leyes de Newton.
3.1.1. Concepto de Fuerza • Tipos • Peso de los Cuer-
pos
El estudio de la mec´nica se remonta a los tiempos de Arist´te-
a o
les y Arqu´ ımedes, pero es Newton(1642 − 1727) quien formula
satisfactoria de sus principios fundamentales. Estos principios
fueron m´s tarde modificados por D’Alembert, Lagrange y Ha-
a
milton. Su validez permaneci´ sin discusi´n hasta que Einstein
o o
formul´ su teor´ de la relatividad en el a˜o de 1905. Aun as´ la
o ıa n ı,
mec´nica Newtoniana sigue siendo la base de las ciencias F´
a ısicas.
El concepto b´sico par la din´mica es la:
a a
Figura 3.1: Joseph Louis Lagrange, Jean le Rond d’Alembert y William Ro-
wan Hamilton.
• Fuerza: Representa la acci´n de un cuerpo so-
o
bre otro cuerpo, puede ser ejercida por contacto
fisico o por medio de campos.
Una fuerza se caracteriza por su: punto de aplicaci´n, mag-
o
nitud y su direcci´n y se representa por un vector. Todos los
o

218. 206 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
cuerpos interact´an entre s´ por medio de fuerzas. Otras carac-
u ı
ter´
ısticas, se han definidio en la secci´n 1.1
o
Figura 3.2: Vector Fuerza
−→
OF = Magnitud o intensidad [N ]
θx = Direcci´n respecto al eje x grados o radianes.
o
O = Punto de aplicaci´n.
o
→ = Sentido
• Tipos de Fuerzas (Clasificaci´n)
o
En el Plano de acci´n
o
Coplanares: Fuerzas que act´an sobre un mismo plano, forma-
u
do por dos ejes ortogonales de coordenadas: x vs y, x vs z, y vs
z
No coplanares: Fuerzas que act´an en planos distintos. Los ejes
u
de referencia ser´n los ejes de coordenadas x, y, z.
a

219. 3.1 Leyes de Newton. 207
En Direcci´n de su Recta de Acci´n
o o
Concurrentes: Sus rectas de acci´n se cortan en alguna parte
o
en el plano
Colineales: Act´an sobre la misma recta de acci´n
u o
Paralelas:Dos o m´s fuerzas cuyas rectas de acci´n tienen la
a o
misma direcci´n.
o
La superficie sobre
Fuerzas puntuales concentradas, o aisladas:
la cual act´a una fuerza es peque˜o en comparaci´n con la su-
u n o
perficie total del cuerpo correspondiente.
Figura 3.3: Fuerza Puntual
Fuerza distribuida:
La superficie o la longitud sobre la cual act´a la fuerza es
u
significativa para los c´lculos.
a
Carga uniforme constante
Carga Uniforme Variable

220. 208 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Por su Forma de trabajo
Axiales: fuerzas que act´an a lo largo del eje longitudinal cen-
u
troidal del elemento.
De Tracci´n:
o Tienden a halar o estirar el cuerpo sobre el cual
act´an.
u
Compresi´n:
o Tienden a acortar o apretar el cuerpo.
Flexoras: Fuerzas que act´an perpendiculares al eje longitudi-
u
nal centroidal del elemento. Producen flexi´n en el elemento.
o
Torsoras: producen giro alrededor del eje longitudinal
Principio de Transmisibilidad
Basado en las condiciones de los vectores deslizantes, estable-
ce que el efecto externo de una fuerza en un cuerpo r´ıgido, es el
mismo para todos los puntos de aplicaci´n, a lo largo de su l´
o ınea
de acci´n. Sin embargo, su efecto interno depende directamente
o
del punto de aplicaci´n de la fuerza sobre el cuerpo.
o
Uniformes Variables
Figura 3.4: Fuerzas Distribuidas

221. 3.1 Leyes de Newton. 209
• Peso de los Cuerpos.
Arist´teles Naci´ en Estagira, en el a˜o 384
o o n
a.C. al norte de la Grecia actual, en el seno de una
familia de m´dicos. Cuando ten´ dieciocho a˜os
e ıa n
se traslad´ a Atenas para formarse como fil´sofo
o o
en la Academia de Plat´n, donde permaneci´ du-
o o
rante los siguientes veinte a˜os.
n
Tras la muerte de Plat´n, Arist´teles dej´ Atenas y vivi´ du-
o o o o
rante alg´n tiempo en Asia Menor, en la corte de un tirano que
u
hab´ sido condisc´
ıa ıpulo suyo y se cas´ con una hija adoptiva
o
de ´ste personaje. Posteriormente Filipo, rey de Macedonia, lo
e
llam´ a su corte y le encarg´ la educaci´n de su hijo Alejan-
o o o
dro [Magno]. Poco despu´s de iniciar el reinado de Alejandro,
e
Arist´teles regres´ a Atenas y fund´ su escuela, el Liceo, donde
o o o
despleg´ una importante labor de investigaci´n y ense˜anza en
o o n
Axiales de Tracci´n
o Axiales de Compresi´n
o
Flexoras Torsoras
Figura 3.5: Fuerzas Por su Forma de trabajo

222. 210 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
las distintas ramas del saber.
Con la muerte de Alejandro, Arist´teles, tuvo que hacer frente
o
al sentimiento antimacedonio que estall´ en Atenas. Acusado de
o
ate´ısmo, Arist´teles tuvo que exiliarse y se refugi´ en Calcis,
o o
donde morir´ al a˜o siguiente, el 322 a.C., a los 62 a˜os de
ıa n n
edad.
En astronom´ Arist´teles propuso la existencia de un Uni-
ıa, o
verso esf´rico y finito con la Tierra como centro. La parte central
e
compuesta por cuatro elementos: tierra, aire, fuego y agua. En
su F´sica, cada uno de estos elementos tiene un lugar adecuado,
ı
determinado por su peso relativo o “gravedad espec´ ıfica ”.
Cada elemento se mueve, de forma natural, en l´ ınea recta (la
tierra hacia abajo, el fuego hacia arriba) hacia el lugar que le
corresponde, en el que se detendr´ una vez alcanzado, de lo que
a
resulta que el movimiento terrestre siempre es lineal y siempre
acaba por detenerse. Los cielos, sin embargo, se mueven de forma
natural e infinita siguiendo un complejo movimiento circular, por
lo que deben, conforme con la l´gica, estar compuestos por un
o
quinto elemento, que ´l llamaba aither (´ter), elemento superior
e e
que no es susceptible de sufrir cualquier cambio que no sea el de
lugar realizado por medio de un movimiento circular. La teor´ ıa
aristot´lica de que el movimiento lineal siempre se lleva a cabo
e
a trav´s de un medio de resistencia es, v´lida para todos los
e a
movimientos terrestres observables.
Para Arist´teles, el peso de los cuerpos tiene que ver con su
o
“gravedad espec´ıfica”, adem´s, sosten´ que los cuerpos m´s pe-
a ıa a
sados de una materia espec´ ıfica caen de forma m´s r´pida que
a a
aquellos que son m´s ligeros cuando sus formas son iguales, con-
a
cepto equivocado que se acept´ como norma hasta que Galileo
o
llev´ a cabo su experimento con pesos arrojados desde la torre
o

223. 3.1 Leyes de Newton. 211
inclinada de Pisa.
Galileo Galilei Naci´ el 15 de febrero de 1564
o
en Pisa, Italia, muri´ el l8 de enero de 1642 en
o
Arcetri, cerca de Florencia, Italia. Matem´tico,
a
astr´nomo y f´
o ısico, considerado el fundador del
m´todo experimental.
e
Galileo estudia medicina en la Universidad de Pisa y ma-
tem´ticas con un tutor privado. Despu´s de completar el tratado
a e
sobre el centro de gravedad de los s´lidos, llega a dar conferen-
o
cias de matem´ticas en la universidad a la edad de 25 a˜os. Pos-
a n
teriormente pasa a la Universidad de Padua como profesor de
matem´ticas. Una parte substancial de su trabajo est´ relaciona-
a a
do con la mec´nica ya que es el primero en aplicar matem´ticas
a a
para su an´lisis. En 1609 desarrolla el telescopio astron´mico
a o
con una lente convergente y otra divergente.
Empleando planos inclinados y un reloj de agua perfeccio-
nado demostr´ que los objetos tardan lo mismo en caer, inde-
o
pendientemente de su masa (lo que invalidaba los postulados de
Arist´teles), que la velocidad de los mismos aumenta de forma
o
uniforme con el tiempo de ca´ ıda. Sus trabajos sobre mec´nica
a
precedieron la obra del matem´tico y f´
a ısico brit´nico del siglo
a
XVII Isaac Newton.
Para Galileo, el peso de los cuerpos es una propiedad natural,
la cual poseen todos los cuerpos, es la que los obliga a caer en
direcci´n del centro de la tierra. As´ a esa propiedad el llama
o ı
peso, sin definir su significado. Al hablar de la caida de los cuer-
pos dice textualmente: Salviati lleva a Simplicio a aceptar que
en el caso del [movimiento ] del plano hacia abajo la bola baja
espontaneamente debido a que es un cuerpo “grave” con masa.
Lo anterior indica que el peso de los cuerpos tiene que ver

224. 212 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
con la masa de un cuerpo o con la inercia.
Tiene que llegar Newton y mediante la segunda ley, definir lo
que es el peso e inercia de los cuerpos.
3.1.2. Fuerzas de Fricci´n Est´tica y Din´mica.
o a a
El Rozamiento o Friccci´n
o entre dos superficies en contacto ha
sido aprovechado desde los tiempos mas remotos para hacer
fuego frotando madera. En nuestra ´poca, el rozamiento tie-
e
ne gran importancia econ´mica, se estima que si se le prestase
o
mayor atenci´n se podr´ ahorrar much´
o ıa ısima energ´ y recursos
ıa
econ´micos.
o
Hist´ricamente, el estudio del rozamiento comienza con Leo-
o
nardo da Vinci que dedujo las leyes que gobiernan el movimiento
de un bloque rectangular que desliza sobre una superficie plana.
Sin embargo, este estudio pas´ desapercibido.
o
En el siglo XVII Guillaume Amontons, f´ ısico franc´s, redescu-
e
bri´ las leyes del rozamiento estudiando el deslizamiento seco de
o
dos superficies planas. Las conclusiones de Amontons son esen-
cialmente las que se estudian en los libros de F´ ısica General:
Propiedad 1 La fuerza de rozamiento se opone al movimien-
to de un bloque que desliza sobre un plano.
Propiedad 2 La fuerza de rozamiento es proporcional a la
fuerza normal que ejerce el plano sobre el blo-
que.
Propiedad 3 La fuerza de rozamiento no depende del ´rea
a
aparente de contacto.
El cient´
ıfico franc´s Coulomb a˜adi´ una pro-
e n o
piedad m´sa

225. 3.1 Leyes de Newton. 213
Propiedad 4 Una vez empezado el movimiento, la fuerza de
rozamiento es independiente de la velocidad.
Origen del Rozamiento por Contacto. La mayor´ de las super-
ıa
ficies, a´n las que se consideran pulidas son extremadamente
u
rugosas a escala microsc´pica. Los picos de las dos superficies
o
que se ponen en contacto determinan el ´rea real de contacto
a
que es una peque˜a proporci´n del ´rea aparente de contacto (el
n o a
´rea de la base del bloque). El ´rea real de contacto aumenta
a a
cuando aumenta la presi´n (la fuerza normal) ya que los picos
o
se deforman.
Los metales tienden a soldarse en fr´ debido a las fuerzas
ıo,
de atracci´n que ligan a las mol´culas de una superficie con
o e
las mol´culas de la otra. Estas soldaduras tienen que romperse
e
para que el deslizamiento se presente. Adem´s, existe siempre
a
la incrustaci´n de los picos con los valles. Este es el origen del
o
rozamiento est´tico.
a
Cuando el bloque desliza sobre el plano, las soldaduras en
fr´ se rompen y se rehacen constantemente. Pero la cantidad
ıo
de soldaduras que haya en cualquier momento se reduce por de-
bajo del valor est´tico, de modo que el coeficiente de rozamiento
a
cin´tico es menor que el coeficiente de rozamiento est´tico.
e a
Finalmente, la presencia de aceite o de grasa en las super-
ficies en contacto evita las soldaduras al revestirlas de un ma-
terial inerte. La explicaci´n de que la fuerza de rozamiento es
o
independiente del ´rea de la superficie aparente de contacto es
a
la siguiente: Como puede verse en la figura 3.6, la superficie m´sa
peque˜a de un bloque est´ situada sobre un plano. En el di-
n a
bujo situado encima, se ve un esquema de lo que se observar´ ıa
al microscopio: grandes deformaciones de los picos de las dos

226. 214 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
superficies que est´n en contacto. Por cada unidad de superfi-
a
cie del bloque, el ´rea de contacto real es relativamente grande
a
(aunque esta es una peque˜a fracci´n de la superficie aparente
n o
de contacto, es decir, el ´rea de la base del bloque).
a
En la figura 3.7, la superficie m´s grande del bloque est´ si-
a a
tuada sobre el plano. El dibujo muestra ahora que las defor-
maciones de los picos en contacto son ahora m´s peque˜as por
a n
Figura 3.6: Origen del Rozamiento
Figura 3.7: Otra Forma en que Actua el Rozamiento sobre un Cuerpo

227. 3.1 Leyes de Newton. 215
que la presi´n es m´s peque˜a. Por tanto, un ´rea relativamente
o a n a
m´s peque˜a est´ en contacto real por unidad de superficie del
a n a
bloque. Como el ´rea aparente en contacto del bloque es mayor,
a
se deduce que el ´rea real total de contacto es esencialmente la
a
misma en ambos casos.
Ahora bien, las investigaciones actuales que estudian el ro-
zamiento a escala at´mica demuestran que la explicaci´n dada
o o
anteriormente es muy general y que la naturaleza de la fuerza
de rozamiento es muy compleja.
La Fuerza Normal, reacci´n del plano o fuerza que ejerce el
o
plano sobre el bloque depende del peso del bloque, la inclinaci´n
o
del plano y de otras fuerzas que se ejerzan sobre el bloque.
Figura 3.8: Fuerza Normal
Suponiendo que un bloque de masa m est´ en reposo sobre
a
una superficie horizontal, las unicas fuerzas que act´an sobre ´l
´ u e
son el peso P = mg, y la fuerza normal N .
En los siguientes p´rrafos se ver´ como se pueden determinar
a a
las Fuerzas que se mencionaron.
3.1.3. Primera Ley de Newton (• Ley de Inercia).
Por ejemplo se hace una tarea porque el profesor la va a Nadie hace o
deja de hacer
calificar y cotnar´ para el examen si no fuera as´ ¿para que algo si no
a ı,
lo obligan.

228. 216 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
hacerla?
Ahora bien: Si en el universo existiese un solo cuerpo (una
part´
ıcula), nada podr´ interferir con su movimiento, si no hay
ıa
fuerzas sobre ´l, es razonable pensar que no se mueva nunca, si
e
no se estaba moviendo, o que no se detenga nunca si se estaba
moviendo. As´ pens´ Newton para enunciar su primera ley, la
ı o
cual se expresa de la siguiente manera:
Una part´ ıcula libre se mueve con velocidad
constante o sin aceleraci´n.
o
Puesto que con esta ley Newton no ha definido lo que es la
fuerza, entonces esta ley es parte de esa definici´n.
o
Leyendo de nuevo el enunciado se puede concluir:
Las fuerzas son las cosas responsables de los
cambios en el movimiento de los cuerpos.
Cuando se empuja una carretilla, se puede creer que la pri-
mera ley de Newton no es tan cierta como se dice, para que
la carretilla se mueva a velocidad constante, se debe estar em-
pujando constantemente. As´ que parece mentira que sobre un
ı
cuerpo que se mueve a velocidad constante no act´a ninguna
u
fuerza, pero si se piensa; ¿Existen otra interacciones o no? es
Figura 3.9: Fuerza Normal y Rozamiento en un Plano inclinado

229. 3.1 Leyes de Newton. 217
decir ¿hay otros cuerpos que interactuen con la carretilla?
¡Claro que si!, a saber: la gravedad, la fricci´n del piso y la
o
resistencia del aire que son fuerzas que est´n actuando sobre la
a
carretilla.
Entonces, para evaluar la veracidad de la primera ley se debe
considerar el efecto conjunto de todas la fuerzas como una sola,
y a la carretilla como el unico objeto del universo, solo as´ se
´ ı
puede someter a prueba el enunciado con ´xito.
e
La sumatoria o superposici´n de las fuerzas que
o
act´an sobre la carretilla es nula y como consecuen-
u
cia, se mueve con velocidad constante.
Por esta situaci´n en otros textos, la primera Ley de Newton
o
de enuncia como:
1ra ley: Todo cuerpo permanece en estado de
reposo o se mueve con Movimiento Rectilineo uni-
forme, si no existe una fuerza que lo obligue a cam-
biar su estado.
Otra forma: Si la fuerza resultante que act´a sobre una part´
u ıcu-
la es cero, la part´
ıcula permanecer´ en reposo (si originalmente
a
estaban en reposo) o se mover´ con rapidez constante en l´
a ınea
recta (si originalmente estaba en movimiento).
Esto significa que en ausencia de fuerzas, un cuerpo en reposo
seguir´ en reposo, y un cuerpo movi´ndose a velocidad constante
a e
en l´
ınea recta continuar´ haci´ndolo indefinidamente.
a e

230. 218 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
3.1.4. Segunda ley de Newton (• Ley de Fuerza).
2da ley: El cambio de movimiento es siempre
proporcional a la fuerza motriz que se imprime; y
se efect´a en la direcci´n de la l´
u o ınea recta seg´n la
u
cual act´a la fuerza.
u
F = ma (3.1)
Donde:
m = Masa de un cuerpo [kg].
m
a = aceleraci´n obtenida s2
o
F = Fuerza aplicada [N ]
Esta ley proporciona una f´rmula expl´
o ıcita que es una de las
m´s utiles, la aceleraci´n a es una cantidad bien definida, es el
a ´ o
cambio por segundo en la velocidad y tiene direcci´n y sentido,
o
es un vector.
Si la fuerza resultante que act´a sobre una part´
u ıcula es dife-
rente a cero, la part´
ıcula adquirir´ una aceleraci´n proporcional
a o
a la magnitud de la resultante y en direcci´n de esta fuerza
o
resultante.
Cuando se aplica una fuerza a un objeto (“cuerpo”) se acelera
en la direcci´n de la fuerza aplicada. La aceleraci´n es directa-
o o
mente proporcional a la intensidad de la fuerza e inversamente
proporcional a la masa a mover.
La Fuerza es igual al producto de la masa por la aceleraci´n.
o
Si una fuerza cualquiera genera un movimiento, una fuerza doble

231. 3.1 Leyes de Newton. 219
generar´ un movimiento doble, una fuerza triple un movimiento
a
triple, ya sea que la fuerza act´e enteramente y de una vez, o
u
gradualmente y sucesivamente. . .
Frente a la acci´n de una fuerza neta, un objeto experimenta
o
una aceleraci´n directamente proporcional a la fuerza neta e
o
inversamente proporcional a la masa del objeto.
F
a= (3.2)
m
Recuerde, que
F = Fuerza neta [N ].
m = Es la masa sobre la cual act´a la fuerza neta [kg]
u
m
a = Aceleraci´n obtenida s2
o
Es una herramienta poderosa para contestar con precisi´n o
preguntas como las siguientes: ¿qu´ ´rbitas son posibles para
e o
planetas y cometas ante la atracci´n del Sol? ¿Qu´ curva des-
o e
cribe en el aire el ombligo de un ba˜ista que se tira a la piscina
n
desde un tabl´n? ¿Qu´ ´ngulo tiene que darle un futbolista a la
o ea
pelota para que llegue lo m´s lejos posible?, si el Sol y su s´quito
a e
de planetas giran a novecientos mil kil´metros por hora en torno
o
al centro de la galaxia, distante doscientos cuarenta mil billones
de kil´metros, ¿cu´l es la masa contenida en el interior?, etc.
o a
(Respuestas: las ´rbitas posibles son las que se forman por la
o
intersecci´n de un plano con un cono: el c´
o ırculo, la elipse y la
hip´rbola; la curva del ombligo del ba˜ista es una par´bola; el
e n a
´ngulo es de 45 grados si se deja fuera la intervenci´n del aire;
a o
la masa es de unas cien mil millones de masas solares.)
Ernest Mach, que vivi´ en Alemania
o
dos siglos despu´s que Newton, argumen-
e
taba que las leyes de Newton se un´ en
ıan

232. 220 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
una sola: “Cuando dos objetos compac-
tos (“puntos masa” en palabras de f´ısica)
act´an uno sobre el otro, aceleran en di-
u
recciones opuestas y la relaci´n de sus
o
aceleraciones es siempre la misma”.
L´alo de nuevo: no menciona fuerzas ´ masas, solo acelera-
e o
ci´n, la cual puede medirse. Cuando una pistola act´a sobre una
o u
bala, un cohete sobre su chorro, el Sol sobre la Tierra (en la es-
cala de la distancia que los separa, el Sol y la Tierra pueden ser
vistos como objetos compactos), las aceleraciones son siempre
opuestas.
La masa y la fuerza se derivan f´cilmente. Si uno de los obje-
a
tos es un litro de agua, su masa se define como un kilogramo. Si
luego act´a sobre otro objeto (quiz´s, para el experimento, con
u a
el agua convertida en hielo), la relaci´n de su aceleraci´n aw con
o o
la aceleraci´n del otro objeto da la masa del objeto m:
o
aw m
= =m
a 1kg
Luego
ma = 1 kg.aw
esto se puede interpretar diciendo que una unidad de fuerza
de magnitud aw existe entre las dos
F = ma = 1 [kg] .aw
Esa unidad de fuerza ser´ la fuerza que causa que 1kg se acelere
a
a 1 s2 , esto es, su velocidad se incrementa cada segundo en 1 m
m
s
Es pues correcto llamar a esa unidad el Newton.

233. 3.1 Leyes de Newton. 221
Gravedad y Peso de los Cuerpos.
Un cuerpo cayendo, tanto si es ligero como si es pesado, tiene
m
la misma aceleraci´n g : 9,8 s2 ↓.
o
¿Donde entra F = ma aqu´ ı?
Newton llam´ a la fuerza que produce la citada aceleraci´n
o o
gravitaci´n, y propuso que era proporcional a la masa. Esa fuer-
o
za, medida en Newtons, con m en kilogramos, es
F = mg ↓
Sustituyendo esto en la expresi´n F = ma, da
o
mg = ma (3.3)
⇒a=g
La ultima l´
´ ınea indica que la aceleraci´n de un objeto cayendo
o
siempre es igual a g, tanto si es un guijarro como una gran roca.
La fuerza que tira de la roca hacia abajo, su “peso”, es mucho
mayor: no obstante su masa, la inercia que deber´ vencer para
a
moverla, es grande tambi´n, con el mismo factor. La conclusi´n
e o
es que, grande ´ peque˜a, la aceleraci´n siempre es igual a g.
o n o
Masa Gravitacional o Masa Inercial. Surge aqu´ un problema; la
ı
masa de un objeto puede ser medida de dos maneras diferentes:
Compar´ndose con la masa de un litro de agua, usando la gra-
a
vedad al pes´rla. Se Obtiene la masa gravitatoria; indicandose
a
como m.
Al prescindirse de la gravedad, como los astronautas abordo
del Skylab y medir la “masa inercial”, llam´ndola M.
a
El f´
ısico h´ngaro Roland E¨tv¨s (Lo-
u o o
rand en h´ngaro) compar´ las dos a lo
u o

234. 222 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
largo de un siglo usando instrumentos
muy sensibles y lleg´ a la conclusi´n que
o o
eran las mismas con una precisi´n de va-
o
rios decimales. Esta igualdad se convir-
ti´ en una de las bases de la f´
o ısica, en
especial de la teor´ general de la relati-
ıa
vidad.
Ejemplo: 3.1.4.1 Objetos en Descanso.
Cuando se est´ de pi´ en el suelo, la
a e
gravedad contin´a tirando su cuerpo ha-
u
cia abajo ( ver figura 3.1.4 a la izquierda)
con fuerza
F = mg ↓
Por qu´ no cae? ¡Porque el suelo no le deja! Las part´
e ıculas
integrantes del suelo est´n juntas y no permiten a su pi´s bajar
a e
m´s (como lo har´ si estuviera sobre arenas movedizas). El he-
a ıa
cho de que la fuerza F no produzca aceleraci´n es la evidencia
o
de que otra fuerza, opuesta al movimiento, es producida por el
suelo: F ′ = −mg (hacia arriba) F y F ′ se suman y su resultante
es cero, sus pies y su cuerpo quedan quietos.
Regla General: si nada cambia, las fuerzas suman cero. El cuer-
po est´ “en equilibrio”, un concepto que ser´ muy util en la
a a ´
pr´xima secci´n. Tome nota de que no tiene nada que ver con la
o o
3a ley de Newton: la 3a ley se ocupa de las fuerzas que producen
el movimiento, mientras que aqu´ todas las fuerzas se cancelan.
ı

235. 3.1 Leyes de Newton. 223
Ejemplo: 3.1.4.2
Calcule la normal que una mesa ejerce
sobre un cuerpo de 10kg de masa, si el
cuerpo est´ en reposo.
a
Soluci´n
o Si el cuerpo est´ en reposo significa que su aceleraci´n
a o
total es nula. Entonces aplicando la segunda ley de Newton
Fx = max = m(0) = 0
a un eje vertical se tendr´ que:
a
Fy = may = mg + N = 0
donde se ha supuesto que la mesa est´ perfectamente horizontal
a
y por tanto la normal tendr´ s´lo una componente en el eje;
a o
0 = mg + N
en este caso
−mg = N
Ejemplo: 3.1.4.3 La fuerza normal, reacci´n del plano o fuerza
o
que ejerce el plano sobre el bloque depende del peso del bloque,
la inclinaci´n del plano y de otras fuerzas que se ejerzan sobre
o
el bloque;
Cuando un bloque de masa m est´ en reposo sobre una super-
a
ficie horizontal (figura 3.10), las unicas fuerzas que act´an sobre
´ u
´l son su peso P = mg y la fuerza normal N . Por las condiciones
e
de equilibrio se obtiene que P = N = mg la fuerza normal es
igual al peso.

236. 224 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Pero si el plano est´ inclinado un ´ngulo θ (figura 3.11), el
a a
bloque est´ en equilibrio en sentido perpendicular al plano in-
a
clinado por lo que la fuerza normal N es igual a la componente
del peso perpendicular al plano, es decir: N = mg cos θ
Considerando de nuevo el bloque sobre la superficie horizon-
tal. Si se ata una cuerda al bloque que forme un ´ngulo θ con la
a
horizontal, la fuerza normal N , deja de ser igual al peso P . La
condici´n de equilibrio de traslaci´n en la direcci´n perpendicu-
o o o
lar al plano establece que la fuerza normal N sea igual al peso
P = mg menos la componente de la fuerza Fy = F sin θ que es
perpendicular al plano.
N = mg − F senθ
Figura 3.10: Diagrama Representando la Fuerza Normal (ej. 3.1.4)
Figura 3.11: Diagrama Representando Plano Inclinado (ej. 3.1.4)

237. 3.1 Leyes de Newton. 225
Fuerza de Rozamiento Cin´tico
e
Un bloque arrastrado por una fuerza F horizontal. Sobre el
bloque act´an el peso P = mg, la fuerza normal N que es igual al
u
peso, y la fuerza de rozamiento Fk entre el bloque y el plano sobre
el cual desliza. Si el bloque se desliza con velocidad constante
la fuerza aplicada F ser´ igual a la fuerza de rozamiento Fk . Si
a
se duplica la masa m del bloque colocando encima de ´ste otro
e
igual cuando se desliza, la fuerza normal N se duplica, la fuerza
F con la que jala el bloque, tambi´n se duplica y por tanto, Fk se
e
duplica. La fuerza de rozamiento din´mico Fk es proporcional a
a
la fuerza normal N . Recordar que las proporcionalidades se ven
en el apendice 1
Fk = µk N (3.4)
La constante de proporcionalidad µk es un n´mero sin dimen-
u
siones que se denomina coeficiente de rozamiento cin´tico.
e
El valor de µk es casi independiente del valor de la velocidad
para velocidades relativas peque˜as entre las superficies, y de-
n
crece lentamente cuando el valor de la velocidad aumenta. Pero
es diferente para cada material que se desliza, por lo que existen
tablas de Valores para los coeficientes de rozamiento.
Ejemplo: 3.1.4.4 Un cuerpo de 4kg est´ deslizando por una su-
a
perficie lisa con coeficiente de rozamiento (din´mico) µk = 0,25.
a
Si sobre este cuerpo no act´an m´s fuerzas que el peso y dicha
u a
fuerza de rozamiento ¿con qu´ aceleraci´n se mueve el cuerpo?.
e o
Aplicando la ecuaci´n de Newton al eje vertical.
o
En este eje, las fuerzas que aparecen son el peso y la normal
y, por tanto;
N +P =0

238. 226 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
⇒ N = −P = −mg
Como un cuerpo sobre una superficie plana no va rebotando
sobre ella, por lo que su altura, medida sobre la superficie, es
siempre 0, se tendr´ que. Aplicando al eje horizontal, se tiene
a
que la unica fuerza en el eje es la de rozamiento, y la que lo
´
acelera, por tanto
Fx − Fr = 0
⇒ Fx = Fr
max = µk N
⇒ max = µk mg
⇒ ax = µk g
m
ax = (0,25)(−9,81
s2
Cuadro 3.1: Coeficientes de Rozamiento Cin´tico para Diferentes Materiales.
e
Superficies en contacto µk
Acero sobre acero 0.18
Acero sobre hielo (patines) 0.02-0.03
Acero sobre hierro 0.19
Hielo sobre hielo 0.028
Patines de madera sobre hielo y nieve 0.035
Goma (neum´tico) sobre terreno firme
a 0.4-0.6
Correa de cuero (seca) sobre metal 0.56
Bronce sobre bronce 0.2
Bronce sobre acero 0.18
Roble sobre roble en la direcci´n de la fibra
o 0.48

239. 3.1 Leyes de Newton. 227
m
ax = −2,45
s2
El signo negativo (−) se debe a que, como el cuerpo avanza
hacia la derecha, el rozamiento se opondr´ al avance y tender´,
a a
por tanto, a detenerse.
Ejemplo: 3.1.4.5 Un bloque de masa 100kg inicia a moverse,
despu´s de 5 segundos, alcanza una velocidad de 10 m , la fuerza
e s
de rozamiento cinetico es de 500N .
Soluci´n al Ejemplo:3.1.4.5
o
a) ¿Cual es la fuerza Normal?
Aplicando la ecuaci´n de Newton al eje vertical.
o
En este eje, las fuerzas que aparecen son el peso y la normal
y, por tanto;
N +P =0
⇒ N = −P = −mg
m
⇒ N = −(100kg) −9,81
s2
N = 981N,
la cual es la fuerza normal(N )
b) ¿Cual es la aceleraci´n que adquiere?
o
por la ec. (2.8)
vf − vi
a=
tf − ti
10 m − 0
s
a=
5s − 0
m
a=2 2
s

240. 228 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
c) ¿Cual es la fuerza que lo acelera?
Sobre el eje x
Fa − Fr = max
⇒ Fa = max + Fr
m
Fa = (100kg) 2 2 + 500N
s
Fa = 700N
c) ¿Cual es el coeficiente de rozamiento cin´tico (µk )?
e
Por la ec. (3.4)
Fk = µk N
aqui Fk es la fuerza de rozamineto, es decir Fr , en tonces:
Fr = µk N
Fr
⇒ µk =
N
500N
µk =
981N
µk = 0,5097
Fuerza de Rozamiento Est´tico.
a
Tambi´n existe una fuerza de rozamiento entre dos objetos
e
que no est´n en movimiento relativo
a
en la figura la fuerza F aplicada sobre el bloque aumenta
gradualmente, pero el bloque permanece en reposo. Como la
aceleraci´n es cero la fuerza aplicada es igual y opuesta a la
o
fuerza de rozamiento est´tico Fe .
a
F = Fe

241. 3.1 Leyes de Newton. 229
La m´xima fuerza de rozamiento corresponde al instante en el
a
que el bloque est´ a punto de deslizar.
a
Femax = µe N
La constante de proporcionalidad µe se denomina coeficiente de
rozamiento est´tico.
a
Los coeficientes de rozamiento est´tico y din´mico dependen
a a
de las condiciones de preparaci´n y de la naturaleza de las dos
o
superficies y son casi independientes del ´rea de la superficie de
a
contacto.
Desde el origen O hasta el punto A la fuerza F aplicada
sobre el bloque no es suficientemente grande como para moverlo.
Estamos en una situaci´n de equilibrio est´tico
o a
F = Fe < µe N (3.5)
En el punto A, la fuerza de rozamiento Fe alcanza su m´ximo
a
valor µe N
F = Femax = µe N (3.6)
Si la fuerza F aplicada se incrementa un poquito m´s, el bloque
a
comienza a moverse. La fuerza de rozamiento disminuye r´pi- a
damente a un valor menor e igual a la fuerza de rozamiento
cin´tico,
e
Fk = µk N (3.7)
Si la fuerza F no cambia, punto B, y permanece igual a Femax
el bloque comienza movi´ndose con una aceleraci´n
e o
(F − Fk )
a= (3.8)
m
Si incrementamos la fuerza F , punto C, la fuerza neta sobre el
bloque F − Fk se incrementa y tambi´n se incrementa la acele-
e
raci´n.
o

242. 230 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
En el punto D, la fuerza F aplicada es igual a Fk por lo que
la fuerza neta sobre el bloque ser´ cero. El bloque se mueve con
a
velocidad constante.
En el punto E, se anula la fuerza aplicada F , la fuerza que
act´a sobre el bloque es -Fk , la aceleraci´n es negativa y la ve-
u o
locidad decrece hasta que el bloque se detiene.
Cuadro 3.2: Coeficientes de Rozamiento Est´tico y Din´mico para Diferentes
a a
Materiales.
Superficies en contacto µe µk
Cobre sobre acero 0.53 0.36
Acero sobre acero 0.74 0.57
Aluminio sobre acero 0.61 0.47
Caucho sobre concreto 1.0 0.8
Madera sobre madera 0.25-0.5 0.2
Madera encerada sobre nieve h´meda
u 0.14 0.1
Tefl´n sobre tefl´n
o o 0.04 0.04
Articulaciones sinoviales en humanos 0.01 0.003
Rozamiento en Fluidos.
El rozamiento con un fluido se expresa como:
Fr = µf v (3.9)
Cuando aumenta la velocidad del flujo, el rozamiento depende
de la velocidad al cuadrado como:
Fr = µf v 2 u
ˆ (3.10)

243. 3.1 Leyes de Newton. 231
Problemas
1. Sobre un cuerpo de 20kg, apoyado en un plano horizon-
tal, act´an dos fuerzas concurrentes de 10N cada una, que
u
forman entre s´ un ´ngulo de 60 ◦ . Si no hay rozamiento, cal-
ı a
cula la fuerza resultante que act´a sobre ´l y la aceleraci´n
u e o
que adquiere.
2. Por un tramo recto y horizontal de una autov´ circula un
ıa
cami´n cuya tara es de 6ton, siendo su carga de 25ton.
o
Cuando el veloc´ ımetro se˜ala 72 km , el cami´n acelera y, en
n h o
km
un minuto, alcanza una velocidad de 90 h . Despreciando
la acci´n de las fuerzas de rozamiento, ¿qu´ fuerza “ha he-
o e
cho el motor” en esa variaci´n de la velocidad? Expresa el
o
resultado en unidades S.I.
3.1.5. 3a Autoevaluaci´n
o
Nombre del alumno Gpo. 30
I.- Subraya la Respuesta Correcta a las Siguientes Preguntas
1. ¿Qu´ son las leyes de Newton?
e
a) son tres principios concernientes al movimiento de los
cuerpos b) leyes que rigen la gravedad c) leyes que explican
el fin y el inicio de la humanidad
2. ¿Desde cuando se remonta el estudio de la mec´nica?
a
a) desde los tiempos de Arist´teles y Arqu´
o ımedes b) desde
que el hombre es un ser pensante c) desde el descubrimiento
de la rueda
3. ¿Por quien fue publicada la formulaci´n matem´tica?
o a
a) por Isaac Newton b) por Edisson c) por kepler

244. 232 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
4. ¿en que a˜o se public´ la formulaci´n matem´tica?
n o o a
a) en 1687 b) en 1234 c) en 1678
5. ¿Qu´ constituye la base de la mecanica clasica?
e
a) las leyes de Newton b) leyes de Keplar c) ley de la gra-
vitaci´n universal
o
6. ¿Qu´ constituye la primera ley de Newton?
e
a) Definici´n de fuerza a causa de la velocidad de los cuer-
o
pos b) A toda acci´n le corresponde una reacci´n c) Todo
o o
lo que sube tiene que bajar
7. ¿Qu´ introduce en fisica, la primera ley de Newton?
e
a) introduce el concepto del sistema de referencia inercial b
)que el cuerpo permanece inerte hasta que es empujado por
una fuerza c) el cuerpo en movimiento mantiene su fuerza
inicial
8. ¿Qu´ es la fuerza?
e
a) es la acci´n mediante la cual cambia el estado de un
o
cuerpo b) es la cantidad de energ´ que agregas a tus mo-
ıa
vimientos c) es cuanta fuerza pones a un aparato
9. ¿Qu´ mostraron Newton y Galileo?
e
a) que los cuerpos se mueven a velocidad constante y en
l´
ınea recta si no hay fuerzas que act´en sobre ellos b) que
u
la tierra era redonda c) que el universo y los cuerpos tienen
un constante
10. ¿con que otro nombre se le conoce a la segunda ley de New-
ton?
a) ley de la fuerza b)ley de la gravitaci´n universal c)ley de
o
la inercia

245. 3.1 Leyes de Newton. 233
11. ¿ que hace la segunda ley de Newton?
a) relaciona las fuerzas actuantes y la variaci´n de la can-
o
tidad de movimiento o momento lineal b)explica como los
cuerpos mantienen una aceleraci´n constante y que solo
o
cambian cuando esta fuerza es detenida. c) que la acelera-
ci´n es constante y que solo los cuerpos en reposo pueden
o
cambiarla.
12. ¿Cu´ndo formul´ Einsten su teor´ de la relatividad?
a o ıa
a) en 1905 b) en 1985 c) en 2005
13. ¿Por qu´ se caracteriza una fuerza?
e
a) por su punto de aplicaci´n, magnitud y su direcci´n b)
o o
por el punto de inclinaci´n y aceleraci´n c) por el punto de
o o
energ´
ıa
14. ¿como se representa una fuerza?
a) por medio de un vector b) por medio magnitud c) por el
punto de inclinacion
15. ¿Como se representa Newton?
a) (N) b) n c) NW
16. ¿como se representa el punto de aplicaci´n?
o
a) (O) b)p. c)p.a
17. ¿Qu´ son las fuerzas no coplanares?
e
a) son Fuerzas que act´an en planos distintos. Los ejes de
u
referencia b) son las fuerzas que no est´n encarreradas c)
a
son fuerzas en el mismo plano pero con diferente valor
18. ¿Qu´ son la fuerzas coplanares?
e
a) Fuerzas que act´an sobre un mismo plano, formado por
u

246. 234 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
dos ejes b) Fuerzas que actuan en diferentes planos c) fuer-
zas que act´an paralelamente
u
19. ¿Cu´les son las fuerzas concurrentes?
a
a) Sus rectas de acci´n se cortan en alguna parte en el
o
plano b) Son fuerzas que no tienen punto de interseccion
y que actuan en diferente plano c) son fuerzas que actuan
paralelamente con otras eb diferente plano
20. ¿que son las fuerzas colineales?
a) son las que act´an sobre la misma recta de acci´n b) Son
u o
las que actuan sobre diferente plano c) Son las que act´an
u
sobre una recta paralele con otra
21. ¿Qu´ son las rectas paralelas?
e
a) son dos a mas fuerzas cuyas rectas de acci´n tienen la
o
misma direcci´n b) Son rectas que se intersectan entre si c)
o
son rectas que tienen una distancia determinada
22. ¿Qu´ son las fuerzas puntuales?
e
a) es cuando La superficie sobre la cual act´a Una fuerza es
u
peque˜o en comparaci´n con la superficie total del cuerpo
n o
Correspondiente. b) Es cuando una superficie liza es relati-
va con la otra c) Es cuando la fuerza de uno es mayor que
otra
23. ¿Qu´ significa fuerza distribuida?
e
a) cuando La superficie o la longitud sobre la cual act´a u
la fuerza es significativa para los c´lculos. b) Es cuando la
a
fuerza se encuentra compacta c) Es la longitud sobre la cual
la aumenta o disminuye la fuerza
24. ¿Qu´ son las fuerzas axiales?
e
a) son fuerzas que act´an a lo largo del eje longitudinal
u

247. 3.1 Leyes de Newton. 235
centroidal del Elemento. b) son fuerzas que intersectan en
un punto determinado c) las fuerzas axiales tienen fuerza
propia
25. ¿Qu´ son las fuerzas de atracci´n?
e o
a) tienden a estirar el cuerpo sobre el cual act´an b) Con-
u
traen el cuerpo sobre el cual actuan c) Se atraen una a la
otra
26. ¿Qu´ son las fuerzas de comprensi´n?
e o
a) tienden a acortar o apretar el cuerpo b) tienden a partir
un cuerpo c) atraen los cuerpos
27. ¿Qu´ son las fuerzas flexoras?
e
a) son fuerzas que act´an perpendiculares al eje longitudi-
u
nal centroidal del elemento b) son fuerzas que actuan sobre
un eje en particular c) son fuerzas que actuan sobre un eje
de diferente plano
28. ¿que son las fuerzas torsoras?
a) son las que producen giro alrededor del eje longitudinal
b) son fuerzas que no tienen giro c) son fuerzas que tienen
un giro en direccion contraria al eje
29. ¿ que establece el principio de transmisibilidad?
a) establece que el efecto externo de una fuerza en un cuerpo
r´
ıgido es el mismo para todos los puntos de aplicaci´n a lo
o
largo de su l´
ınea de acci´n b) es cuando tienen las fuerzas
o
actuan a lo largo de eje c) Es la superficie sobre la cual
actuan las fuerzas flexoras
30. ¿Qu´ importancia tiene el rozamiento, en nuestra ´poca?
e e
a) tiene una gran importancia econ´mica b) mucho ya que
o
esta inmerso en nuestro contexto c) genera ingresos

248. 236 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
31. ¿con quien comienza el estudio del rozamiento?
a) con Leonardo Da vinci b) con Galileo Galilei c) con Isaac
newton
32. ¿que hizo Leonardo Da Vinci respecto al rozamiento?
a) dedujo las leyes que gobiernan el movimiento de un blo-
que rectangular que desliza sobre una superficie plana b)
dedujo que el movimiento se desliza sobre una base liza c)
dedujo que es imposible tener rozamiento sobre una super-
ficie plana
33. ¿Qui´n redescubri´ las leyes del rozamiento?
e o
a) Galileo y Einstein
b) Pericles
c) El f´
ısico franc´s Guillaume Amontons
e
34. ¿en que siglo se redescubrieron las leyes del rozamiento?
a) en el siglo XVII b) en el siglo XVI c) en el siglo XV
35. ¿Qu´ otro nombre tiene la primera ley de Newton?
e
a) ley de la inercia b) ley del movimiento de los cuerpos c)
tercera ley de Newton
36. ¿a que se refiere la ley de inercia?
a) nadie hace o deja de hacer algo si no lo obligan b) que
un cuerpo en movimiento puede hacer cambiar a otro c) un
cuerpo solo permanece inerte hasta que se detiene
37. ¿Como se expresa la primera ley de Newton?
a) una part´ıcula libre se mueve con velocidad constante
o sin aceleraci´n b) Una particula solo tiene aceleraci´n
o o
cuando esta en contacto con otra c) una particula libre se
mueve con aceleracion

249. 3.1 Leyes de Newton. 237
38. ¿Qu´ son las fuerzas?
e
a) son las cosas responsables de los cambios en el movi-
miento de los cuerpos. b) son los cambios de velocidad c)
son los cambios de longitud
39. ¿Qui´n era Isaac Newton?
e
40. ¿Cu´ntas leyes descubri´?
a o
41. ¿Cu´les fueron?
a
42. ¿ Que es la inercia?
43. ¿ Que pasa cuando esta se detiene?
44. ¿Qu´ es sistema de referencia inercial?
e
45. ¿C´mo se considera la relatividad?
o
46. ¿Qu´ es velocidad?
e
47. ¿Qu´ es fuerza?
e

250. 238 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
3.1.6. Tercera Ley de Newton (• Ley de Acci´n y Reac-
o
ci´n).
o
El universo est´ formado por todos los cuerpos materiales, y
a
entre ellos existen interacciones que se manifiestan como fuerzas
ejercidas por unos sobre los otros. Si se suman todas estas fuerzas
la resultante es nula, cada fuerza tiene una compa˜era que la
n
equilibra. Este es el contenido de la tercera ley.
A cada acci´n se opone siempre una reacci´n igual: o las
o o
acciones mutuas de dos cuerpos uno sobre el otro, son siempre
iguales, y dirigidas en sentido contrario. · · · . Las fuerzas son
siempre producidas en pares, teniendo direcciones opuestas e
igual magnitud. Si el cuerpo 1 act´a con una fuerza F sobre el
u
cuerpo 2, el cuerpo 2 actuar´ sobre el 1 con una fuerza de igual
a
intensidad y direcci´n opuesta.
o
3ra ley: Las fuerzas de acci´n y reacci´n entre
o o
cuerpos en contacto tienen la misma magnitud, la
misma l´ınea de acci´n y sentidos opuestos.
o
Esta ley se puede interpretar diciendo que nadie va a hacer lo
que le obliguen as´ nada m´s. Va a oponer resistencia. Mientras
ı a
m´s lo obliguen, m´s resistencia opone.
a a
En un sistema donde ninguna fuerzas externas est´n presente,
a
cada fuerza de acci´n son iguales y opuestas, adquiriendo velo-
o
cidades inversas proporcionales a sus masas. Si usted presiona
una piedra con su dedo, el dedo tambi´n es presionado por la
e
piedra· · · Si un cuerpo golpea contra otro, y debido a su fuerza
cambia el movimiento del otro cuerpo, ese cuerpo tambi´n su-
e
frir´ un cambio igual, en su propio movimiento, hacia la parte
a
contraria. Los cambios ocasionados por estas acciones son igua-

251. 3.1 Leyes de Newton. 239
les, no en las velocidades sino en los movimientos de los cuerpos;
es decir, si los cuerpos no son estorbados por alg´n impedimento
u
Figura 3.12: Acci´n y Reacci´n de la Tercera Ley de Newton
o o
Fab = −Fba (3.11)
o bien;
Matem´ticamente la tercera ley del movimiento de Newton
a
suele expresarse como sigue:
F1 = F2
donde F1 es la fuerza que act´a sobre el cuerpo 1 y F2 es la
u
fuerza reactiva que act´a sobre el cuerpo 2. En una aplicaci´n
u o
combinada de la segunda y tercera ley de Newton se tiene que:
m1 a1 = m2 a2
donde los sub´
ındices est´n referidos a los cuerpos 1 y 2.
a
Ejemplo: 3.1.6 La fuerza de atracci´n F1 que ejerce la Tierra
o
sobre un objeto en su superficie es igual y opuesta a la fuerza
de atracci´n F2 que emite el objeto. Ambos, la Tierra y objeto
o
se aceleran, pero como la masa de la Tierra es inmensamente
mayor, la aceleraci´n de efecto que recibe es ´
o ınfima comparada

252. 240 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
con la que experimenta el objeto (su masa comparativa es muy
peque˜a). A ello se debe la raz´n del por qu´ nosotros se puede
n o e
percibir la aceleraci´n de un objeto que cae sobre la superficie
o
m
de la Tierra, que es de 9,81 s2 ; sin embargo, no se detecta la ace-
leraci´n de la Tierra, que es de aproximadamente 1,5 X 10−21 cm
o s2
para un objeto de 90 kg.
Ejemplo: 3.1.6 Cuando dos cuerpos comportan masas semejan-
tes, como un par de estrellas binarias, entonces podr´ observar
ıase
la aceleraci´n de ambas masas.
o
3.1.7. Ley de la Gravitaci´n Universal.
o
Los antecedentes de esta ley se fundamentan en los estudios
de Tycho Brahe y Johannes Kepler, por lo que se mencionar´na
brevemente.

253. 3.1 Leyes de Newton. 241
Tycho Brahe Sin instrumentos, sola-
mente con una esfera y un comp´s, consi-
a
gui´ detectar graves errores en las tablas
o
astron´micas de la ´poca y se dispuso
o e
a corregirlos. Era un observador meticu-
loso que pas´ a˜os estudiando los movi-
o n
mientos de los planetas, el Sol y la Lu-
na. Los datos, obtenidos con instrumen-
tos dise˜ados por ´l, eran sorprendente-
n e
mente precisos y tuvieron un papel cru-
cial para el desarrollo de la astronom´ ıa,
nunca acept´ totalmente el sistema de
o
Cop´rnico del Universo por lo que busc´ una
e o
forma de compromiso entre el de Cop´rni-
e
co y el antiguo sistema de Tolomeo. El
sistema de Brahe presupon´ que los cin-
ıa
co planetas conocidos giraban alrededor
del Sol, el cual, junto con los planetas,
daba una vuelta alrededor de la Tierra
una vez al a˜o. La esfera de las estrellas
n
giraba una vez al d´ alrededor de la Tierra inm´vil.
ıa o
La teor´ de Brahe sobre el movimiento de los planetas era
ıa
defectuosa, pero los datos que obtuvo durante su vida desem-
pe˜aron un papel fundamental en el desarrollo de la descripci´n
n o
correcta del movimiento planetario

254. 242 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Johannes Kepler utiliz´ los datos de
o
Brahe para desarrollar sus tres famosas
leyes del movimiento planetario.
Las Leyes de Kepler.
Estas leyes han tenido un significado especial en el estudio de
los astros, ya que permitieron describir su movimiento; fueron
deducidas emp´ ıricamente por Johannes Kepler (1571 − 1630) a
partir del estudio del movimiento de los planetas, para lo cual se
sirvi´ de las precisas observaciones realizadas por Tycho Brahe
o
(1546 − 1601). S´lo tiempo despu´s, ya con el aporte de Isaac
o e
Newton (1642 − 1727), fue posible advertir que estas leyes son
una consecuencia de la llamada Ley de Gravitaci´n Universal.
o
Primera Ley de Kepler, puede enunciarse de la siguiente mane-
ra:
Los planetas en su desplazamiento alrededor del Sol describen
elipses, con el Sol ubicado en uno de sus focos.
Debe tenerse en cuenta que las elipses planetarias son muy
poco exc´ntricas (es decir, la figura se aparta poco de la cir-
e
cunferencia) y la diferencia entre las posiciones extremas de un
planeta son m´ ınimas (a la m´xima distancia de un planeta al
a
Sol se denomina afelio y la m´ ınima perihelio). La Tierra, por
ejemplo, en su m´ ınima distancia al Sol se halla a 147 millones

255. 3.1 Leyes de Newton. 243
de km, mientras que en su m´xima lejan´ no supera los 152
a ıa
millones de km.
Segunda ley de kepler, puede expresarse como:
Las ´reas barridas por el segmento que une al Sol con el pla-
a
neta (radio vector) son proporcionales a los tiempos empleados
para describirlas.
Esta ley implica que el radio vector barre ´reas iguales en
a
tiempos iguales; esto indica que la velocidad orbital es variable a
lo largo de la trayectoria del astro siendo m´xima en el perihelio
a
y m´ ınima en el afelio (la velocidad del astro ser´ constante si la
ıa
´rbita fuera un c´
o ırculo perfecto). Por ejemplo, la Tierra viaja a
km
30,75 s en el perihelio y “rebaja” a 28, 76 km en el afelio.
s
Tercera ley, finalmente, dice que:
El cuadrado del per´ ıodo de revoluci´n de cada planeta es
o
proporcional al cubo de la distancia media del planeta al Sol.
La tercera ley permite deducir que los planetas m´s lejanos
a
al Sol orbitan a menor velocidad que los cercanos; dice que el
per´
ıodo de revoluci´n depende de la distancia al Sol.
o
Pero esto s´lo es v´lido si la masa de cada uno de los plane-
o a
tas es insignificante en comparaci´n con la del sol. Si se quisiera
o
calcular el per´
ıodo de revoluci´n de astros de otro sistema plane-
o
tario, se deber´ aplicar otra expresi´n com´nmente denominada
ıa o u
tercera ley de Kepler generalizada.
Esta ley generalizada tiene en cuenta la masa del planeta y
extiende la tercera ley cl´sica a los sistemas planetarios con una
a
estrella central de masa diferente a la del Sol.
Por otra parte, Newton menciona en el libro Philosophiae
Naturalis Principia Mathematica [1687] (Principios matem´ti- a

256. 244 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
cos de la filosof´ natural): . . . Y el mismo a˜o comenc´ a pensar
ıa n e
que la gravedad se extiende a la ´rbita de la Luna y . . . deduje
o
que las fuerzas que mantienen los planetas en sus ´rbitas deb´
o ıan
de ser proporcionales a la inversa de los cuadrados de sus dis-
tancias a los centros alrededor de los que giran; en consecuencia,
compar´ la fuerza necesaria para mantener la Luna en su ´rbita
e o
con la fuerza de la gravedad en la superficie de la Tierra, y en-
contr´ que la respuesta era muy aproximada. Todo esto fue en
e
los a˜os de la plaga de 1665 − 1666. Porque en ellos yo estaba
n
en mi mejor edad mental para la invenci´n y me interesaban
o
las matem´ticas y la filosof´ m´s que en ninguna otra ´poca
a ıa a e
1
posterior.
Establece que dos part´
La Ley de la gravitaci´n de Newton:
o ıcu-
las de masa M y m se atraen mutuamente con fuerzas iguales y
opuestas F y −F de magnitud F dado por la expresi´n:
o
1
v´ase [22]
e
Figura 3.13: Figura que muestra las tres leyes de Kepler

257. 3.1 Leyes de Newton. 245
m1 m2
F =G u
ˆ (3.12)
d2
12
donde:
m1 Es la masa de un cuerpo [kg]
m2 Corresponde a la masa de un segundo cuerpo [kg]
d12 Distancia entre los centros de ambos cuerpos [m]
F Fuerza de gravedad mutua entre ellos [N ], y
G Constante de la Gravitaci´n Universal, que vale: 6.67 ×10−11
o
Nm2
kg 2
u = Vector unitario en direcci´n de la fuerza.
ˆ o
La constante gravitacional G, fue estimada por primera vez
tal vez por Galileo2 , posteriormente la forma de medirla fue idea-
da por Jhon Michell y en el siglo XVIII, en 1798 fue medida por
Sir Henry Cavendish (1731 − 1810), a quien se le conoce co-
mo el pesador del mundo. Un aparato similar fue utilizado por
Coulomb para el estudio de las fuerzas el´ctricas y magn´ticas.
e e
Se atribuye que el primer cient´
ıfico que logr´ estimar la cons-
o
tante de gravedad fue Galileo, cuando realiz´ el experimento de
o
lanzar dos pelotas de diferentes masas desde la c´spide de la
u
Torre de Pisa, las cuales cayeron con una aceleraci´n constante,
o
pero es un antecedente que no se encuentra confirmado.
2
tal vez en su honor Newton le llam´ G a la constante
o

258. 246 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Actividad. 3.1.7.1
1. Realice una investigaci´n sobre: Que es, como es, y como se
o
utiliza una “Balanza de Cavendish”.
2. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
3. para la evaluaci´n se tomar´ en cuenta:
o a
a) Entrega en tiempo y forma (una semana m´ximo).
a
b) Claridad en lo escrito.
c) Coherencia de lo escrito.
d ) Validez y pertinencia de las ideas expuestas (que tenga
relaci´n con la situaci´n actual).
o o
e) Presentaci´n.o
f ) Profundidad del escrito.
Ejemplo 3.1.7.1 Utilizando una Balanza de Cavendish se mi-
dio la fuerza de atracci´n entre dos personas, una con masa de
o
50kg y otra de 70kg, las cuales est´n separadas 1mm. ¿Cuanto
a
marc´ la escala de fuerza?
o
Soluci´n al Ejemplo 3.1.7.1
o Por la ecuaci´n (3.12)
o
m1 m2
F =G
d2
12
2
−11 Nm (60kg)(70kg)
F = 6,67 × 10
kg 2 (1 × 10−3 m)2
F = 0,28N
es la fuerza equivalente al peso de: 28,6 gramos.

259. 3.1 Leyes de Newton. 247
Ejemplo 3.1.7.2 La fuerza de atracci´n de la tierra sobre una
o
masa de 1Kg es de 9,81N , el radio medio de la tierra es 6380km.
Calcule la masa de la tierra.
Soluci´n al Ejemplo 3.1.7.2
o Por la ecuaci´n (3.12)
o
m1 m2
F =G
d2
12
2
−11 Nm (1kg)mt
9,81N = 6,67 × 10
kg 2 (6380 × 103 m)2
donde mt indica la masa de la tierra.
mt = 5,98 × 1024 kg
asi procedi´ Cavendish para conocer la masa de la tierra.
o
El volumen de la tierra (considerandola esf´rica) es:
e
4
V = πr3
3
4
V = π(6380000m)3
3
V = 1,0878 × 1021 m3
y su densidad es:
m
̺=
V
5,98 × 1024 kg
̺=
1,0878 × 1021 m3
kg kg
̺ = 5497 ≈ 5500 3
m3 m

260. 248 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Problemas
1. En un experimento con la balanza de Cavendish, se reali-
zaron las siguientes mediciones:
m1 = 0,8kg
m2 = 0,004kg
f = 13 × 10−11 N
d = ,04m
Calcule con esto datos el valor de la constante de gravita-
ci´n universal (G)
o
1
2. La masa de la luna es de 81 de la masa de la tierra, su radio
1
4 del de la tierra, la distancia de separaci´n entre estos
o
cuerpos es de 300000km
a) ¿Con que fuerza se atraen?
b) ¿Cual sera la atracci´n de la luna sobre un cuerpo? o
o
de otra manera ¿Cual es la aceleraci´n de la gravedad
o
en la luna?
3.2. Trabajo, Potencia y Energ´ Mec´nica.
ıa a
Arqu´ımedes da a partir de proposicio-
nes pr´cticamente autoevidentes, la ley
a
de la palanca que permite introducir el
concepto de trabajo en f´ısica. Suponien-
do que se quier elevar un peso con una
palanca cuya relaci´n de tama˜o de los
o n
brazos es 3:1, entonces por presi´n sobre
o

261. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 249
el extremo de la palanca se puede hacer
con una fuerza tres veces menor que el
peso de la piedra. La distancia que se ha
movido la piedra es obviamente tres ve-
ces menor que el desplazamiento que ha
realizado [28]-[31], por lo que se cumple
que:
F uerzaaplicada × desplazamiento = P esode la piedra × altura
F ·d=P ·h
El principio de la palanca se aplic´ a otro aparato que utiliz´ Ar-
o o
qu´ımedes para sorprender al rey Hieron moviendo el solo un gran
barco: la polea.
3.2.1. Trabajo.
El define el trabajo T como el producto de la fuerza F por el
desplazamiento d
T =F ·d (3.13)
por lo que la ley de la palanca implica que el trabajo (T ) in-
vertido para levantar la piedra es exactamente el mismo que el
necesario para elevar un peso (P ) en contra de la gravedad. Re-
cordando que la fuerza (F ) se mide en Newton [N ], la distancia
en metros [m].
Con estas unidades, el trabajo se ex-
presa en [N m] Cantidad que se denomi-
na Joule en honor al f´
ısico brit´nico Ja-
a
mes Prescott Joule quien centr´ sus in-
o

262. 250 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
vestigaciones en los campos de la electri-
cidad y la termodin´mica.
a
Demostr´ que el calor es una transferencia de energ´ y deter-
o ıa
min´ el equivalente mec´nico del calor. En espa˜ol esta cantidad
o a n
se traduce como Julio.
Una caracter´ ıstica importante que debe ser notada es que el
producto est´ representado en esta expresi´n por medio de un
a o
“punto ” (·), lo que significa un producto especial un producto
escalar el cual es un producto entre dos vectores que da como
resultado un escalar.
Un Joule o Julio es el trabajo realizado por una
fuerza de 1 N aplicada para producir un desplaza-
miento de 1 m.
3.2.2. Potencia.
Mide la rapidez con que se realiza un trabajo.
La potencia es igual al trabajo realizado dividi-
do entre el intervalo de tiempo a lo largo del cual
se efect´a dicho trabajo.
u
En t´rminos matem´ticos;
e a
T
P = (3.14)
t

263. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 251
El concepto de potencia no se aplica exclusivamente a situa-
ciones en las que se desplazan objetos mec´nicamente, resulta
a
util, por ejemplo, en electricidad.
´
La potencia siempre se expresa en unidades de energ´ di- ıa
vididas entre unidades de tiempo. La unidad de potencia en el
Sistema Internacional es el vatio [W ], que equivale a la potencia
necesaria para efectuar 1 julio [J] de trabajo por segundo [s].
La potencia, se nombra as´ en honor
ı
a James Watt (1736 − 1819), inventor
e ingeniero mec´nico escoc´s quien realiz´ me-
a e o
joras a la m´quina de vapor y determin´ las
a o
propiedades del vapor, en especial la re-
laci´n de su densidad con la temperatura
o
y la presi´n.
o
Existe la idea extendida, pero equivocada, de considerar a
Watt como el inventor de la m´quina de vapor, ´sta se debe al
a e
gran n´mero de aportaciones que hizo para su desarrollo.
u
La unidad de potencia tradicional es el caballo de vapor (CV),
que equivale aproximadamente a 736 vatios.
Caballo de vapor:
Unidad tradicional para expresar la potencia mec´nica, es de-
a
cir, el trabajo mec´nico que puede realizar un motor por unidad
a
de tiempo; suele abreviarse por CV. En el Sistema Internacio-
nal de unidades, la unidad de potencia es el vatio; 1 caballo de
vapor equivale a 736 vatios. Su valor original era, por definici´n,
o
75 kilogr´metros por segundo.
a

264. 252 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
El kW − Hr
Las compa˜ias de generaci´n de electricidad, en M´xico la
n o e
CFE, miden la energ´ utilizada por el usuario no en Joules ni
ıa
en calorias sino en una unidad llamada kW − Hr, (kilowat-hora
o kilovatio por hora), esta cantidad resulta de multiplicar la
potencia en kilovatios por una hora de uso, por lo que puesto
que: 1W = 1 J , 1kW = 1000W y 1Hr = 3600s, entonces:
s
1kW − Hr = 1,000W − Hr
1kW − Hr = (1,000W ) · (3,600s) = 3,600,000W · s
1J
1kW − Hr = 3,600,000 ·s/
s
/
1kW − Hr = 3,600,000J
En M´xico a esta unidad, la compa˜ia le asigna un valor de
e n
acuerdo a cuantos kW − Hr se utilicen y la zona del pa´ don-
ıs
de se encuentre el usuario, dividiendose en tres costos; B´sico,
a
Intermedio y Excedente, el cual en abril del 2,007 en Tlaxcala,
ten´ los siguientes costos3 :
ıa
Cuadro 3.3: Costo por kW − Hr en Tlaxcala abril 2,007
Concepto l´ ımite (kW − hr) costo (Pesos)
B´sico
a > 0a150 0,63
Itermedio > 150a250 0,74
Excedente > 250 2,00
preguntas
1) ¿Qu´ es el trabajo mec´nico?.
e a
3
Tomado directamente de un recibo de la CFE

265. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 253
2) ¿En que unidades se mide el trabajo?.
3) ¿Cu´les son sus equivalencias?.
a
4) Si se levanta un cuerpo desde el suelo, ¿hay trabajo?.
5) ¿Las m´quinas simples, realizan trabajo?.
a
Ejercicios
1) Transformar 250 kgm a Joule y kW · hr.
R. : 2450 J y 0, 0007 kW · hr.
2) ¿Cu´ntos kgm y Joule representan 25 kW · hr.?.
a
R. : 9,10J y 9183673 kgm
3) Indicar cu´ntos Joul y kW.h son 125478 kgm.
a
R. : 12296844 J y 3, 4 kW · hr.
4) Indicar el trabajo necesario para deslizar un cuerpo a 2 m de
su posici´n inicial mediante una fuerza de 10 N.
o
R. : 20 J
5) ¿Qu´ trabajo realiza un hombre para elevar una bolsa de 70
e
kgf a una altura de 2, 5 m?. Expresarlo en:

266. 254 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
a) kgm. R.
: 175 kgm
b) Joule. R.
: 1715 J
c) kWh. R.
: 0, 00047 kW · hr.
6) Un cuerpo cae libremente y tarda 3 s en tocar tierra. Si su
peso es de 4 N, ¿qu´ trabajo deber´ efectuarse para elevarlo
e a
hasta el lugar desde donde cayo?. Expresarlo en:
a) Joule. R.
:1728, 7 J
b) kgm. R.
:176,4 kgm
3.2.3. Energ´ Mec´nica (Potencial y Cin´tica).
ıa a e
Energ´ potencial gravitacional.
ıa
Para levantar un peso (P ) con una palanca hasta una altura
(h) se tiene que realizar un trabajo (T )
T =P ·h
Pero, si el cuerpo se encuentra a una altura h y cae, puede
realizar un trabajo desde la altura h, esto es; es capaz de reali-
zar trabajo. Esta reflexi´n lleva decir que se tiene una Energ´
o ıa
potencial gravitacional en la cantidad P · h, pero de (3.3)
Ep = P · h = m · g · h (3.15)

267. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 255
m
ahora bien en la secci´n 2.1.5, se mencion´ que g = 9,81 s2
o o
hacia abajo y se demostr´ en la secci´n 3.1.4.
o o
Una interesante propiedad es que sl el trabajo realizado para
llevar un cuerpo hasta una altura h es independiente de la mane-
ra en que uno lo sube hasta all´ Esto conduce a diferenciar dos ti-
ı.
pos de sistemas, a saber: Conservativos y no-conservativos.
Ejemplo:3.2.3.1 Con esta propiedad es sencillo realizar muchos
problemas que se suelen hacer en la ense˜anza media con planos
n
inclinados. Suponiendo que se tiene un plano inclinado de lados
3, 4 y 5 metros y una masa de 1 kg situado en la base. Queriendo
calcular el peso P que colocar en el extremo de la cuerda para
que el sistema est´ en equilibrio. Eso significa que en equilibrio
e
los pesos pueden ser desplazados a un lado y a otro sin esfuerzo
(esto no es cierto en la realidad, solamente en donde no existiera
rozamiento en ninguna parte del sistema) lo cual significa que
se puede cambiar la energ´ potencial del cuerpo de peso P en 5
ıa
P mientras la energ´ potencial del cuerpo de 1Kg s´lo cambia
ıa o
en 3 unidades. Si el trabajo realizado por el cuerpo de peso P
tiene que ser igual al realizado sobre el peso de 1kg, se tiene que
5P = 3
3
⇒ P = kg
5
Esta relaci´n puede deducirse de la manera que figura en el
o
epitafio de la tumba de Simon Stevin (1548 − 1620).
Es tambi´n util para darse cuenta que el peso efectivo de
e ´
un cuerpo que se mueve por un plano inclinado est´ en la misma
a
relaci´n al peso del cuerpo como la relaci´n entre la altura que
o o
sube el plano por unidad de distanica recorrida sobre el plano.
Esa relaci´n es el seno del ´ngulo de inclinaci´n del plano.
o a o

268. 256 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Energ´ Cin´tica.
ıa e
Energ´ relacionada con el movimiento:
ıa
Cuando se suelta un p´ndulo que se encuentra a una altura
e
h respecto a su altura m´ınima, este pierde una energ´ potencial
ıa
igual a P · h ¿Hacia d´nde se va esa energ´ potencial?. Bueno,
o ıa
el p´ndulo despu´s de pasar por el punto m´s bajo se sigue
e e a
moviendo y vuelve a subir hasta la misma altura por el otro
lado. ¡La energ´ potencial se recupera de nuevo!. La diferencia
ıa
consiste en que en los momentos intermedios el cuerpo est´ en
a
movimiento. Parece que debe existir una energ´ relacionada con
ıa
el movimiento.
Calculando el trabajo necesario para llevar un cuerpo desde
el reposo hasta una velocidad v. Suponiendo que la forma en
que se lleve al cuerpo hasta esa velocidad no va a afectar a la
energ´ que posea, que se hace con una aceleraci´n uniforme a
ıa o
en un tiempo conocido t, es decir se cumple la expresi´n (2.8)
o
∆v
a = ∆t
El trabajo es entonces
T = F · d = ma · d
la ultima parte de esta expresi´n se parece a la que se utiliz´ en
´ o o
la secci´n 2.1.5, ecuaci´n: (2.17), con la salvedad que aqu´ se usa
o o ı
d y en esa parte se us´: x, pero finalmente son desplazamientos.
o
Utilizando el resultado de la expresi´n (2.17), se tiene:
o
2 2
2 2
vf − vo
2ax = vf − vo ⇒ ax =
2
2 2
vf − vo
T = max = m
2

269. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 257
que se puede escribir
1 2 2
T = m vf − vo (3.16)
2
que significa que el trabajo se conviente en un cambio en las
cantidades:
1 2
mv (3.17)
2
y esta es la expresi´n de la energ´ cin´tica.
o ıa e
1
Ec = mv 2 (3.18)
2
Lo anterior significa que la energ´ potencial se convierte en
ıa
cin´tica y la cin´tica en potencial de tal manera que la suma de
e e
ambas es siempre constante. Esa es una forma de establecer un
principio de conservaci´n muy importante en f´
o ısica: el principio
de conservaci´n de la energ´
o ıa.
3.2.4. Principio de Conservaci´n de la Energ´ Mec´ni-
o ıa a
ca.
La energ´ mec´nica es la suma de las energ´ cin´tica y
ıa a ıas e
potencial.
Em = Ec + Ep (3.19)

270. 258 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
El principio de conservaci´n asegura que
o
Em =constante.
Una forma sencilla de formular este principio es:
la cantidad de Energ´ Cin´tica gastada se con-
ıa e
vierte en potencial o viceversa.
Ejemplo: 3.2.4.1 Se tira un objeto hacia arriba con una veloci-
dad de 30 m , ¿hasta que altura ser´ capaz de llegar?.
s a
2
Inicialmente el cuerpo tiene una energ´ cin´tica Ec = 1 m 30 m
ıa e 2 s
Esta energ´ es convertida en energ´ potencial Ep = mgh,
ıa ıa
por lo que:
1 m 2
m 30 = mgh
2 s
despejando h
1
2m/ 900 mm
ր
ւ
s2
=h
m
ւ
m 9,81ր
/ s2
⇒ h = 45,9m
Se resolvi´ el problema sin aplicar la cinem´tica, pero me-
o a
diante la cual el lector debe comprobar el resultado.
¿tiene limitaciones este principio de conservaci´n?. Si el lector
o
considera un choque de dos objetos que permanecen posterior-
mente unidos, parece que existe una p´rdida de energ´ cin´tica.
e ıa e
Por ejemplo, en el caso de dos masas que se aproximan con velo-
cidad v y chocan para formar una masa 2m en reposo, ¿a d´nde o
va la energ´ cin´tica?. Se pueden hacer dos sugerencias:
ıa e

271. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 259
1. La energ´ cin´tica desaparece
ıa e
2. La energ´ cin´tica se convierte en otra forma de energ´
ıa e ıa
que queda almacenada en los cuerpos.
Pero el principio de conservaci´n de la energ´ tiene un car´cter
o ıa a
general, por lo que se debe admitir la existencia de otras formas
de energ´ıa.
Ejemplo: 3.2.4.2 A nadie le extra˜a que dos cuerpos que chocan
n
de frente se deforman y calientan. Entonces; la energ´ cin´tica
ıa e
se ha convertido en energ´ calor´
ıa ıfica.
Ejemplo: 3.2.4.3 Cuando dos objetos chocan como dos bolas de
billar. En ese tipo de choques (conocidos como choques inel´sti-
a
cos) ocurre considerar que la energ´ cin´tica s´ que se conser-
ıa e ı
va. Puede uno imaginarse que los cuerpos que sufren el choque
inel´stico est´n unidos por peque˜os muelles.
a a n
Ejemplo: 3.2.4.4 Un muelle o resorte, tiene la propiedad de de-
volver la energ´ que se le proporciona, as´ como el campo gravi-
ıa ı
tacional cuando se levanta una piedra, mediante una compresi´no
adquiere energ´ potencial y una descompresi´n realiza trabajo,
ıa o
claro que en un muelle real existe la posibilidad de una defor-
maci´n que hace que no toda la energ´ proporcionada para la
o ıa
compresi´n se pueda devolver en la descompresi´n posterior.
o o
Ejemplo: 3.2.4 El caso de una pelota de superficie bien tersa que
bota sucesivamente en el suelo. Si el choque fuera exactamente
el´stico ascender´ siempre a la misma altura, pero un jugador
a ıa
de baloncesto sabe perfectamente que tiene que imprimir una

272. 260 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
peque˜a fuerza al bal´n para mantenerlo a suficiente altura, el
n o
hecho es que un bal´n termina por parar despu´s botar.
o e
Ejemplo: 3.2.4.5 La elasticidad perfecta es una aproximaci´n
o
excelente cuando chocan dos part´ ıculas subat´micas o cuando
o
un cometa es desviado de su trayectoria por la proximidad de
un cuerpo celeste como un planeta o una estrella.
Ejercicio: 3.2.4.1Un aeroplano vuela a 20m debajo de otro ae-
roplano del mismo tama˜o y peso. Ambos viajan a una velocidad
n
m
de crucero de 600 s .
a) Qu´ aeroplano tiene energ´ m´s cin´tica?
e ıa a e
b) Cu´l tiene m´s energ´ potencial?
a a ıa
Ejercicio: 3.2.4.2 Imagine que usted est´ en un columpio, osci-
a
lando en el patio.
a) En qu´ punto en su oscilaci´n usted va a tener mayor
e o
energ´ cin´tica?
ıa e
b) En qu´ punto usted tiene m´s energ´ potencial?
e a ıa
nota: Responda realizando un diagrama para cada ejercicio.
3.2.5. Impulso y Cantidad de Movimiento.
Para Descartes, la Cantidad de Movimiento estaba relaciona-
da con el producto de la materia y la rapidez, pero su idea de la
esencia de la materia no era la masa, sino el volumen. Newton
redefine tal noci´n, definiendo cantidad de movimiento, o mo-
o
mento lineal como el producto de la masa y la velocidad. Esto es
el ´
ımpetu de Buridan reinterpretado f´ısicamente y muy parecido
al momento de Galileo ( peso por velocidad).

273. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 261
La tercera ley de Newton conduce directamente al principio
fundamental de la conservaci´n del momento lineal; esta ley es-
o
tablece que:
Si se quiere cambiar la cantidad de movimiento
de un cuerpo se tiene que ejercer un impulso sobre
el.
La cantidad de movimiento antes y despu´s debe de ser igual
e
para que se cumpla la ley.
Cantidad de Movimiento
La cantidad de movimiento se representa por la letra p se
define como:
producto de la masa de un cuerpo por su velo-
cidad.
Es decir:
p=m·v (3.20)
La cantidad de movimiento tambi´n se conoce como momen-
e
to (o mom´ntum). Es una magnitud vectorial y, en el Sistema
e
Internacional se mide en kg · m .
s

274. 262 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Impulso
Aplicaci´n de una fuerza constante que act´a
o u
sobre un sistema durante un lapso de tiempo (no
indefinidamente):
I = F · (tf − ti )
I = F · ∆t (3.21)
(la fuerza se tiene que escribir con su signo y el impulso tam-
bi´n, hay que tener cuidado con su sentido y direcci´n)
e o
Las unidades del impulso son: N · s.
Si lo que se necesita es el impulso de fuerzas no constantes
recurre al gr´fico de fuerzas en funci´n del tiempo, el ´rea dar´ el
a o a a
impulso promedio.
por otra parte, el cambio en la cantidad de movimiento pro-
ducido en un cuerpo por una fuerza externa, depende de la mag-
nitud de la fuerza y tambi´n del tiempo que esta act´a sobre el
e u
cuerpo.
De acuerdo con la segunda ley de Newton, se tiene:
= ma
∆v
=m
∆t
∆(mv)
=
∆t

275. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 263
∆p
F= (3.22)
∆t
pudiendo enunciarse la siguiente ley, (enunciada por New-
ton): La variaci´n de la cantidad de movimiento de un cuerpo
o
es proporcional a la fuerza que act´a sobre el.
u
De la ecuaci´n anterior si se despaja ∆p, se deduce que
o
F ∆t = ∆p (3.23)
El producto de la fuerza por el tiempo que esta act´a es el
u
impulso (I), el cual mide la variaci´n de l cantidad de movimien-
o
to producida por la fuerza durante el tiempo de su aplicaci´n,o
pudiendo escribirse que, en un intervalo de tiempo, la variaci´n
o
total de la cantidad de movimiento vendr´ dada por:
a
∆p = F ∆t (3.24)
En la ecuaci´n (3.24) el valor de la fuerza puede ser interpre-
o
tado como el valor medio de la misma durante el intervalo de
la variaci´n. En un impacto la fuerza no permanece casi nun-
o
ca constante durante el intervalo de tiempo de la colisi´n, sino
o
que var´ dentro de unos l´
ıa ımites muy grandes. Por tanto, la Ec.
(3.22) determina el valor medio de la fuerza durante el intervalo
de contacto. Si es preciso conocer la fuerza en un instante dado
de la colisi´n, esta vendr´ determinada por la variaci´n de la
o a o

276. 264 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
cantidad de movimiento en ese instante. Siendo muy dif´ co-
ıcil
nocer esa variaci´n, se puede, sin embargo, estudiar la fuerza en
o
funci´n de la deformaci´n producida en el momento del choque.
o o
Las ecuaciones (3.22) indican que ning´n objeto puede ser
u
parado instant´neamente y que cuanto mas corto es el interva-
a
lo requerido para detener un cuerpo tanto mayor puede ser la
fuerza necesaria para conseguirlo. Una bomba tirada desde una
altura de varios miles de metros, tendr´ una gran cantidad de
a
movimiento en el impacto. Si el blanco es un barco, se parara en
un corto espacio de tiempo o atravesara la cubierta del barco.
La cubierta acorazada de un barco es, generalmente, insuficiente
para impedir la penetraci´n de la bomba, por que las fuerzas en
o
juego son extremadamente grandes. El signo negativo del resul-
tado indica que la fuerza es de sentido opuesto a la velocidad,
dando un resultando l´gico.
o
Por (3.21), (3.23) y (3.24), se tiene
I = ∆p (3.25)
Esta ecuaci´n significa que el Impulso es igual al cambio en
o
la cantidad de movimiento es decir el impulso no se pierde sino
que se convierte en un Cambio en la cantidad de movimiento.
Esto conduce al:
3.2.6. Principio de la Consevaci´n de la Cantidad de
o
Movimiento.
Dos esferas se desplazan en direcciones opuestas, con veloci-
dades v1a y v2a (la letra (a) indica que es antes de chocar), sus

277. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 265
cantidades de movimiento son p1 y p2 respectivamente, puesto
que sus masas son m1 y m2
Antes del Choque En el Momento del Choque Despu´s del Choque
e
Figura 3.14: Choque de Dos Cuerpos
En un momento dado chocan como se muestra en la figura
(3.14).
Por la tercera ley de Newton la fuerza que ejerce cada una de
ellas es igual pero de sentido opuesto.
F = −F
Multiplicando ambos miembros por el cambio en el tiempo;
F∆t = −F∆t
por (3.25)
I = −I
Obtenemos el impulso, pero como se mostr´ anteriormente,
o
I = ∆p
Entonces:
∆p1 = −∆p2
∆p1 + ∆p2 = 0

278. 266 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
p1d − p1a + p2d − p2a = 0
⇒ p1d + p2d = p1a + p2a (3.26)
Es decir que la suma de las cantidades de movimiento despu´s e
de un choque son iguales a la suma de cantidades de movimiento
antes de un choque.
Este resultado aunque se obtuvo para una dimensi´n es v´lido
o a
para otras dimensiones.
3.2.7. Colisiones (Choques)
Si se imagina a dos machos cabr´ con sus imponentes cor-
ıos
namentas, enfrentados en un combate por un territorio repleto
de hembras. Los dos magn´ ıficos animales se levantan sobre sus
patas traseras “impuls´ndose” para descender a topetazos sobre
a
su oponente. Este violento encuentro ilustra perfectamente la
situaci´n de una colisi´n donde act´an fuerzas externas relati-
o o u
vamente grandes durante un tiempo estimativamente corto.
Como se puede determinar la posici´n de cada animal durante
o
todo el proceso, podemos tratarlos f´ ısicamente como si fueran
part´ıculas.
Si bien la idea b´sica de una colisi´n es que, en movimiento
a o
o quietas, dos o m´s part´
a ıculas (o por lo menos una de ellas)
cambian bruscamente su direcci´n, lo que es muy evidente es el
o
cambio de velocidad que experimentan las part´ ıculas involucra-
das antes y despu´s del choque.
e
Durante la colisi´n la fuerza var´ de una manera tan com-
o ıa
pleja que resulta muy complicada medirla. Estas fuerzas, deno-
minadas impulsivas, act´an durante un brev´
u ısimo instante.
Lo que hay que estacar es que la cantidad de movimiento
se mantiene constante. La cantidad de movimiento, como se ha

279. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 267
visto, es el producto entre la masa y la velocidad. As´ que se
ı
tendr´ la cantidad de movimiento de cada part´
a ıcula antes y des-
pu´s del choque, la cantidad total de movimiento (la suma de
e
las cantidades de movimientos de ambos cuerpos) ser´n iguales
a
antes y despu´s de chocar.
e
Si ambas part´
ıculas quedaran “adheridas” en un solo cuerpo
en movimiento, el choque se denominar´ pl´stico. Pero si re-
a a
botaran separ´ndose, el choque se designar´ con el nombre de
a a
el´stico.
a
Choque pl´stico (Totalmente Inel´stico)
a a
Las colisiones inel´sticas tienen la peculiaridad de que la
a
energ´ cin´tica aunque se conserva, los objetos que se defor-
ıa e
man no vuelven a su forma original, por lo que en este tipo de
colisiones act´an fuerzas no conservativas como la fricci´n y en
u o
el momento de chocar generan calor.
m1 v1 + m2 v2 = (m1 + m2 )vf (3.27)
Choque el´stico
a
Las colisiones el´sticas son aquellas en que la energ´ cin´tica
a ıa e
total se conserva; por lo que podemos decir que tanto antes como
despu´s de la colisi´n la energ´ cin´tica ser´ la misma.
e o ıa e a
m1 v1a + m2 v2a = m1 v1d + m2 v2d (3.28)
Durante la colisi´n parte de la energ´ cin´tica inicial se convier-
o ıa e
te temporalmente en energ´ potencial a medida que los objetos
ıa
se deforman, luego de la deformaci´n m´xima viene otra eta-
o a
pa donde los objetos regresan a su forma original y el sistema
tiene la misma cantidad de energ´ cin´tica que al principio de
ıa e

280. 268 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
la colisi´n. Tambi´n este tipo de colisiones se caracterizan por
o e
no generar calor. Choque el´stico: golpe percutante Podr´
a ıamos
distinguir dos tipos, el central y el oblicuo seg´n la recta que
u
une los dos centros de gravedad de ambos cuerpos coincida o no
con la direcci´n de sus respectivas velocidades.
o
El estudio del choque oblicuo es muy complejo ya que tiene
en cuenta el c´lculo vectorial de las velocidades considerando los
a
respectivos ´ngulos de incidencia. Por este motivo se limita en
a
el estudio al caso central.
Consideremos el esquema del choque 3.15 c, donde quedan
expuestas las masas ( m ), direcciones (→) y velocidades ( v )
de los cuerpos antes y despu´s del choque : Por tratarse de un
e
choque el´stico se conserva tanto la cantidad de movimiento o
a
momento lineal (definido por el producto de la masa por la velo-
cidad : p = mv ) como la energ´ cin´tica del sistema (definida
ıa e
por el semiproducto de la masa por el cuadrado de la velocidad
: E = 1 mv 2 ).
2
En consecuencia, aplicando ambos teoremas de conservaci´n o
al sistema se obtiene de forma general :
m1 v1a + m2 v2a = m1 v1d + m2 v2d
(ecuaci´n vectorial)
o
1 2 1 2 1 2 1 2
m1 v1a + m2 v2a = m1 v1d + m2 v2d
2 2 2 2
(ecuaci´n escalar)
o
Este sistema consiste en un sistema de ecuaciones, el que
desarrollando matem´ticamente, se obtiene la siguiente soluci´n:
a o
(m1 − m2 ) 2m2
v1d = v1a + v2a (3.29)
(m1 + m2 ) (m1 + m2 )

281. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 269
2m1 (m2 − m1 )
v2d = v1a + v2a (3.30)
(m1 + m2 ) (m1 + m2 )
De este resultado podemos extraer las siguientes conclusiones1 :
a) Si las dos masas de los cuerpos son id´nticas ( m1 = m2 )
e
resulta que :
v1d = v2a
y
v2d = v1a
es decir que los cuerpos intercambian sus velocidades.
b) Si adem´s de ser iguales las masas de los dos cuerpos uno de
a
ellos, por ejemplo el cuerpo 2, est´ en reposo (v2 = 0) se
a
obtiene:
v1d = 0
y
v2d = v1d
es decir que el primero se detiene al chocar y el segundo
adquiere la misma velocidad que llevaba el primero.
c) Si la masa inicialmente en reposo es mucho mayor que la otra
( m2 >> m1 ) se obtiene:
v1d = −v1a
y
v2d = 0
es decir que la primera invierte su velocidad mientras que
la segunda se mantiene en reposo. Este ser´ el caso de un
ıa
golpe de pu˜o o patada en una pared de la cual se saldr´
n ıa
rebotando sin conseguir moverla o derribarla.
1
vease [5]

282. 270 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
d) El caso m´s interesante y real es aquel en el que una de las
a
masas es ligeramente mayor que la otra (m2 > m1 ) mante-
ni´ndose en reposo la segunda (v2 = 0), del cual podemos
e
deducir que :
(m1 − m2 )
v1d = v1a
(m1 + m2 )
2m1
v2d = v1a
(m1 + m2 )
Como se puede apreciar en las f´rmulas a medida que se au-
o
menta la masa del primer cuerpo (m1 ) y se disminuye la del
segundo (m2 ) manteniendo constante la velocidad inicial (v1a )
se obtendr´n mayores velocidades finales.
a
Manteniendo constantes las masas y aumentando la velocidad
de ejecuci´n del mismo (v1 ) se obteniene una mayor velocidad de
o
retroceso (−v1d ) y se imprime mayor velocidad a la otra masa.
Figura 3.15: a.- Una bola en movimiento golpea una bola en reposo. b.-
Colisi´n frontal entre dos bolas en movimiento. c.- Colisi´n de dos bolas que
o o
se desplazan en la misma direcci´n.
o
Ejemplo 3.2.7 Desarrollado:
Una bala de 0, 05 kg. masa se desplaza con una velocidad de
350 m . cuando impacta sobre un bloque de madera, de 0, 36 kg.
s
de masa, incrust´ndose en ´l.
a e

283. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 271
Hallar la velocidad con que se mueve el sistema luego del
choque.
Soluci´n: Al impactar la bala queda incrustada dentro del
o
bloque de madera, por lo cual se puede suponer despu´s del e
impacto ambos cuerpos se desplazan juntos. Se est´ frente a un
a
choque pl´stico, en el cual, antes del choque, la bala se encuentra
a
movi´ndose mientras que el bloque est´ quieto (velocidad inicial
e a
cero).
Datos:
m m
v1 = 350 , m1 = 0, 05kg, v2 = 0 , m = 0, 36kg.
s s
Inc´gnita: v2 = ? (velocidad bala - madera).
o
Aplicando la ecuaci´n del choque pl´stico (3.28) y reempla-
o a
zando por sus respectivos valores.
m1 v1 + m2 v2 = (m1 + m2 )vf
v = vf
m
(350 ) · (0, 05kg) + 0 = v(0, 41kg)
s
m
⇒ v = 42,683
s
Ejercicios
1. Una locomotora que pesa 10000kgf se mueve sobre una
v´ recta y choca contra otra locomotora igual que se ha-
ıa
lla en reposo, moviendose unidas despu´s del choque. Si la
e
km
velocidad de la primera es de 45 hr , calcular:
a) cantidad de movimiento del sistema antes del choque.

284. 272 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
(Resp.: 125,000kg. m )
s
b) la velocidad de ambas m´quinas despu´s del choque.
a e
( Resp.: vf = −6,25 m )
s
c) cantidad de energ´ cin´tica se pierde durante la colisi´n.
ıa e o
( Resp.: 390,625J)
2. Una bala de 10g de masa choca contra un p´ndulo bal´
e ısti-
co cuya masa es de 2kg. Por efecto del choque, la base del
p´ndulo se eleva una altura de 10cm, quedando la bala em-
e
potrada en ´l. Calcular la velocidad inicial de la bala.
e
(Resp.: 280 m )
s
3. Una bala de 2g de masa, que lleva una velocidad de 500 m ,
s
ha sido disparada horizontalmente contra un bloque de ma-
dera de 1kg de masa, que se halla inicialmente en reposo
sobre una superficie horizontal. La bala atraviesa el bloque
y sale de ´l con una velocidad de 100 m , en tanto que el
e s
bloque se desliza una distancia de 20cm sobre la superficie
antes de detenerse. Calcular:
a) el coeficiente de rozamiento entre el bloque y la superfi-
cie.
(
Resp.: µk = 0, 16)
b) la p´rdida de energ´ cin´tica que experimenta la bala.
e ıa e

285. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 273
Resp.: 240J
c) la energ´ cin´tica del bloque inmediatamente despu´s
ıa e e
de ser atravesado por la bala.
Resp.: 0, 32J
3.2.8. Coeficiente de Restituci´n
o
Siempre existe una conversi´n de energ´ a energ´ calor´
o ıa ıa ıfica,
en consecuencia la velocidad despu´s del choque ha de ser menor
e
que la que pose´ antes.
ıa
Por ´sto se introduce el Coeficiente de Restituci´n definido
e o
como :
(v1d − v2d )
r=− (3.31)
(v1a − v2a )
magnitud escalar adimensional que indica el grado de elasticidad
del choque.
Este coeficiente var´ entre 0 (choque perfectamente inel´sti-
ıa a
co) y 1 (choque perfectamente el´stico).
a
Pr´ctica 4.
a
Pr´ctica: Cohete de Agua4
a
Objetivo
Confecci´n de un dispositivo para hacer un estudio cualitativo
o
(observaci´n e identificaci´n de los fen´menos que ocurren) de
o o o
la Tercera Ley de Newton y la Conservaci´n de la Cantidad
o
4
basado en el art´
ıculo obtenido en la p´gina www.ungs.edu.ar/ici/fisica/fisica1/cohete/
a
[26]

286. 274 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
de Movimiento. El dispositivo es de f´cil construcci´n de bajo
a o
costo.
Que pueda ser desarrollado por alumnos de bachillerato, des-
pertado el inter´s del alumno.
e
Introducci´n.
o
La propulsi´n a chorro es una aplicaci´n de la Tercera Ley
o o
de Newton y la conservaci´n de la Cantidad de Movimiento.
o
El cohete gana impulso expulsando el combustible de su inte-
rior hacia afuera de el, como onsecuencia, el cohete ejerce una
fuerza sobre el combustible que escapa y por la Tercera Ley de
Newton, se ejerce una fuerza igual y opuesta sobre el cohete
propuls´ndolo hacia adelante. El momento lineal perdido por el
a
combustible expulsado es igual al momento lineal ganado por el
cohete. Por lo tanto, se concluye que el cohete, se impulsa en
sentido contrario al combustible que escapa.
An´lisis del Movimiento
a
El an´lisis requiere del uso de ecuaciones diferenciales, sin
a
embargo, se realizan aproximaciones que dan un resultado v´lido
a
para este nivel.
Se analiza el sistema total (cohete y combustible expulsado)
ver figura 3.16 para un intervalo determinado de tiempo. Igua-
lando esta variaci´n al impulso ejercido sobre el sistema por las
o
fuerzas externas que act´an sobre ´l. Las variables son:
u e
Fext designa la fuerza externa resultante que act´a sobre el cohe-
u
te.
m es la masa del cohete m´s la cantidad de combustible que se
a
encuentra en su interior.
∆m masa de combustible expulsado.

287. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 275
Figura 3.16: Sistema: Cohete y Combustible expulsado para un intervalo
determinado de tiempo.

288. 276 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
v es la velocidad en el instante t relativa a la tierra (fig. 1a ).
uex Velocidad de expulsi´n del combustible.
o
t es el tiempo en que inicia la salida de combustible.
En un instante posterior:
t + ∆t
la masa del cohete es:
m − |∆m|
moviendose con una velocidad:
v − uex .
Si el combustible es expulsado con una velocidad uex respecto
al cohete, la velocidad respecto a la Tierra en el instante t + ∆t
es
v − uex
El ´
Impetu del sistema en el instante ∆t es:
Fext ∆t = ∆mv (3.32)
El cambio en la cantidad de movimiento del sistema en el ins-
tante t + ∆t es:
∆mv = (m − |∆m|) · (v + ∆v) + |∆m|uex − mv (3.33)
∆mv = m∆v − |∆m|v − |∆m|∆v + |∆m|uex
Donde se elimina (en lenguaje matem´tico, se dice que se des-
a
precia) el t´rmino ∆|m| · ∆v ya que es el producto de dos mag-
e
nitudes muy peque˜as en comparaci´n con las dem´s, cuando
n o a
el intervalo t es muy peque˜o. Igual´ndola al impulso (relaci´n
n a o
3.32), se obtiene:
Fext ∆t = m∆v − |∆m|v + |∆m|uex (3.34)

289. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 277
Dividiendo entre el intervalo de tiempo (∆t);
∆v |∆m| |∆m|
Fext = m − v+ uex
∆t ∆t ∆t
Tomando el l´ ımite cuando ∆t tiende a cero, el t´rmino ∆v se
e ∆t
aproxima a la derivada dv , que es la aceleraci´n, y el t´rmino
dt o e
|∆m| |dm|
∆t se aproxima a − dt , que es el valor absoluto de la variaci´n
o
de la masa del cohete, el signo negativo se debe a que es una
disminuci´n. con respecto al tiempo. As´ se obtiene la ecuaci´n
o ı o
de la Fuerza que impulsa al cohete:
dv d|m| d|m|
Fext = m + v− uex ) (3.35)
dt dt dt
d d|m|
Fext = mv − uex ) (3.36)
dt dt
La magnitud uex |dm/dt| es la fuerza de impulsi´n del cohete.
o
Construcci´n de las alas.
o
El material con el que las alas deben construirse es made-
ra balsa. Las razones principales son el bajo peso y costo de
este material, adem´s de que se puede trabajar f´cilmente. No
a a
Figura 3.17: Forma de las alas, Cualquiera Funcionan Bien
hay recomendaciones acerca de la forma de las alas, cualquiera
funcionan bien.
El pegado de las alas al cohete debe ser relativamente d´bil,
e
esto es porque el cohete impacta contra el piso luego de ser

290. 278 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
lanzado. Si el pegado fuese fuerte es probable que se parta la
madera, en cambio, con un pegamento d´bil se logra que las alas
e
se separen del cohete al chocar con el suelo sin que se rompan.
Construcci´n del Cohete.
o
Paso 1 Paso 2 y 3
Figura 3.18: figuras para la Construcci´n del Cohete.
o
Paso 1 Se debe disponer de dos botellas. Una de las mismas
se utiliza entera y a la otra se corta de manera que el
pico quede con un tercio del total de la botella.
Paso 2 El pico de la botella cortada se inserta en la base de
la botella entera.
Paso 3 Ambas partes se sellan utilizando cualquier tipo de
cinta adhesiva o silic´n fr´ (preferentemente cinta ca-
o ıo
nela).

291. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 279
Procedimiento Experimental.
Paso 1 Conectar el pico inferior del cohete a un tanque de
agua lo m´s alto posible, as´ el agua del interior posee
a ı
mayor energ´ potencial respecto del lugar donde se
ıa
encuentra el cohete.
A mayor altura del tanque de agua se lograr´ un ma-
a
yor llenado del cohete, alcanz´ndose mayores alturas
a
en los lanzamientos.
Paso 2 abrir la v´lvula del agua sosteniendo el cohete mien-
a
tras ingresa agua en ´l. Se llega a un nivel en el que
e
ya no ingresa agua, esto se debe a que la presi´n que
o
ejerce el aire que qued´ en el interior del cohete equi-
o
para a la presi´n que hace el agua que quiere entrar.
o
En este instante se debe soltar el cohete.
Paso 3 Filmar una serie de lanzamientos realizar un estudio
de lo que ocurre observando cuadro por cuadro.
Recomendaciones
En general no se puede lograr que el pico de la botella que se
conecta a la manguera cierre herm´ticamente. Esto genera p´rdi-
e e
das importantes de agua cuando la presi´n dentro del cohete
o
comienza a ser grande.
Una manera de solucionar este inconveniente es utilizar una
3′
manguera de 4 (tres cuartos de pulgada) conectada a un tubo
del mismo di´metro, al que se conecta el cohete. Si a´n se tienen
a u
p´rdidas en esta ultima conexi´n, se debe colocar un anillo o-
e ´ o
ring en el pico de la botella. As´ pr´cticamente se eliminan las
ı a
p´rdidas.
e

292. 280 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
En el “aterrizaje”. Cuando el cohete cae contra el piso suelen
romperse las alas de madera. La manera m´s f´cil de evitar esto
a a
es con un grupo de observadores que “atajen” al cohete antes
de que este se golpee.
La persona que sostiene al cohete hasta lanzarlo resulta mo-
jada, porque el agua que sale del mismo salpica todo lo que esta
a su derredor, lo que se recomienda es “salvese el que pueda”;
hay que correr.
Consejos para las Conclusiones
El aumento de la velocidad del cohete a medida que disminuye
la cantidad de agua dentro del mismo es apreciable a simple
vista, luego, con un simple an´lisis de las fuerzas actuantes en
a
el sistema tambi´n se ve la Tercera Ley de Newton.
e
Un mejor an´lisis se puede hacer si se filma alg´n lanzamien-
a u
to, al pasar el video cuadro por cuadro se aprecia perfectamente
como en cada cuadro la distancia recorrida por el cohete es ma-
yor que la distancia recorrida en el cuadro anterior.
Realizar una investigaci´n sobre cohetes y su implementaci´n.
o o
Realizar un reporte con las cracter´
ısticas necesarias, colocan-
do en la introducci´n un resumen de la investigaci´n realizada.
o o
Los resultados cumplen los objetivos propuestos ya que los
mismos son de car´cter cualitativo.
a

293. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 281
Indicaciones para el Reporte.
1. Conf´rmense en equipos de hasta 5 elementos, nombrando
o
un representante.
2. Se entregar´ un reporte por equipo.
a
3. El reporte de la pr´ctica debe contener:
a
* Presentaci´n. o
* Introducci´n. o
* Desarrollo.
* Conclusiones.
* Bibliograf´ ıa.
4. Discuta en equipo el contenido de cada uno de los puntos
que debe contener el reporte
5. Para el paso llamado desarrollo, tomar como base los men-
cionados anteriormente.
6. Reportarlo como:
1.- Se observ´ que . . .
o
2.- La atura se midi´ con el . . . , porque; . . .
o
3.- . . . . . .
4.- . . . . . . .
7. Realizar un cuadro donde se presenten las mediciones y
c´lculos realizados.
a
8. Discuta en equipo el contenido de las conclusiones y la bi-
bliograf´ ıa.

294. 282 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Para la evaluaci´n de la Pr´ctica 4 se tomar´ en cuenta:
o a a
1. Entrega en tiempo y forma (dos semanas m´ximo).
a
2. Validez y pertinencia de las ideas expuestas.
3. Profundidad de los conceptos.
4. Revisi´n del contenido.
o
5. Presentaci´n a l plantel por el equipo.
o
6. habra una coevaluaci´n por lo que se debe poner de acuerdo
o
con el profesor.
7. La evaluaci´n se reportar´ en un cuadro como el siguiente:
o a
Indicador si no ponder. calif.
Present´ en tiempo y forma
o 1
El reporte contiene
Introducci´n o 1
Desarrollo 2
Conclusiones 1
bibliograf´ıa 1
existe Validez y pertinencia 1
de las ideas expuestas
Existe Claridad y coherencia 1
en el escrito.
Existe Profundidad en los 2
conceptos

295. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 283
3.2.9. 4a Autoevaluaci´n
o
Nombre del alumno ————————————– Gpo. 30—–
I.- Subraya la Respuesta Correcta a las Siguientes Preguntas
1. ¿Qu´ ES EL MRU? a)Es cuando la velocidad solo aumenta
e
o disminuye b)Se parte de la ecuaci´n dada para la acele-
o
raci´n c)Velocidad constante
o
2. ¿ Que SIGNIFICA MRUV? a) Movimiento Rectil´ ıneo Uni-
forme Acelerado b) Movimiento Rectil´
ıneo Uniforme Varia-
do
3. ¿Qu´ DICE AL GALILEO AL RESPECTO CON LA CAI-
e
DA LIBRE?
4. ¿Cu´les son las tres formas de lanzar un pryectil? a) Ti-
a
ro Vertical, altura maxima alcanzada, tiempo que tarda en
subir b) tiro libre tiro vertical tiro horizontal c) Altura ma-
xima alcanzada , tiempo que tarda en subir, tiro libre
5. ¿Que es EL TIRO VERTICAL?
6. ¿Que ES LA ALTURA MAXIMA ALCANZADA?
7. ¿ DE QUE ESTA COMPUESTA LA VELOCIDAD? a) por
la suma vectorial de dos velocidades b) por la velocidad
horizontal c) por la velocidad vertical
8. ¿Qu´ es EL MOVIMIENTO PARABOLICO?
e
9. ¿ Como ES REALIZADO EL MOVIMIENTO PARABO-
LICO? a) en sentido horizontal b) en sentido vertical c)
movimiento en un plano
10. ¿C´mo es el MOVIMIENTO CIRCULAR?
o

296. 284 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
11. ¿C´mo pude SER CARACTERIZADO EL movimiento cir-
o
cular? a) por la medida de la trayectoria b) por el despla-
zamiento angular
12. ¿Dame un ejemplo de movimiento circular
13. ¿C´mo se define EL RADIAN? a) el cociente entre el arco
o
del circulo recorrido y el radio del c´
ırculo b)El radio del
circulo entre el di´metro
a
14. ¿Cuando se dice que se ha recorrido EL PERIMETRO DEL
CIRCULO?
15. ¿Cu´ndo se dice que es un MCU?
a
16. ¿Qu´ ES MCUV?
e
17. ¿Cu´les son las caracter´
a ısticas que presenta el MCU?
18. ¿ Por que se dice que son inversas las definiciones de periodo
y frecuencia?
19. ¿COM SE DEFINE la velocidad ANGULAR?
20. ¿ DA LA DEFINICION DE VELOCIDAD LINEAL?
21. ¿D´nde NACIO ARISTOTELES? a) Naci´ EN Estagira b)
o o
Nacio en Grecia c) Nacio en Europa
˜
22. ¿En que ANO NACIO ARISTOTELES? A) 384 a. c. b)
500 a.c. c) 450 a.c.
23. ¿ DONDE NACIO GALILEO GALILEI?
24. ¿En que a˜o NACIO GALILEO GALILEI?
n
25. ¿ EN QUE FECHA MUERE GALILEO GALILEI?

297. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 285
26. ¿ EN QUE LUGAR MURIO?
27. ¿Qu´ ES LA FUERZA?
e
28. Una FUERZA POR QUE SE REPRESENTA?
29. ¿ que CARACTERIZA A UNA FUERZA? A) Punto de
apliaccion B) magnitud c) Por su doreccion
30. CUALES SON LOS TIPOS DE FUERZAS? a) coplanares
b) no coplanares c) por vectores
31. MENCIONA cuales son las fuerzas COPLANARES
32. MENCIONA cuales son las fuerzas NO COPALNARES
33. Menciona cuales son los que van en direccion de su recta
de accion a( concurrentes b) colineales c) Paralelos
34. CUALES SON Las fuerzas CONCURRENTES
35. CUALES SON LAS fuerzas COLINEALES?
36. CUALES SON LAS fuerzas PARALELAS?
37. CUALES SON LAS FUERZAS AISLADAS? l
38. CUAL ES una FUERZA DISTRIBUIDA
39. Son una de las fuerzas por su acci´n a) axiales b) de traccion
o
c) de comprensi´n d) flexoras e) torsoras
o
40. CUALES SON LAS fuerzas AXIALES
41. ¿Cu´les SON LaS fuerzas DE TRACCION?
a
42. CUALEs SON LaS fuerzas DE COMPREsI´N?
o

298. 286 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
43. CUAlesS SON LAS fuerzas FLEXORAS?
44. ¿Cu´les SON LAS fuerzas TORSORAS?
a
45. de un ejemplo de fuerza flexora
46. ¿Cu´l esLA FUERZA DE ROZAMIENTO?
a
47. ¿Explique EL PRINCIPIO DE TRANSMISIBILIDAD? a)
Basado en las condiciones de los vectores deslizantes b) Es-
tablece el efecto externo de una fuerza en un cuerpo rigido
c) Establece que la acci´n es la misma para todos lo puntos
o
de aplicaci´n
o
48. ¿Cu´l ES EL ORIGEN DEL ROZAMIENTO AL CON-
a
TACTO? a) son extremadamente rugosas a escala micros-
copica b) Los picos de las dos superficies se ponen en con-
tacto determina el area c) es una peque˜a proporcion del
n
area rela de contacto
49. ¿Qu´ ES AL FUERZA NORMAL? a) Re accion del plano o
e
fuerza que ejerce el planmo sobre el bloque b)La inclinaci´n
o
del plano c) otras fuerza que ejrcen en el bloque
50. ¿dibuja una FUERZA NORMAL?
51. ¿Qu´ dice LA PRIMERA LEY DE NEWTON?
e
a)ticula libre se mueve con velocidad constante o sin acele-
raci´n b) nadie hace o deja de hacer algo si no lo obligan
o
c) todo cuerpo permanece en estado de reposo o se mue-
ven con movimientos rectilineos unoforme si no existe una
fuerza que lo obligue a cambiar su estado.
52. ¿Qu´ son las leyes de Newton?
e
a) son tres principios concernientes al movimiento de los

299. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 287
cuerpos b) leyes que rigen la gravedad c) leyes que explican
el fin y el inicio de la humanidad
53. ¿Desde cuando se remonta el estudio de la mec´nica?
a
a) desde los tiempos de Arist´teles y Arqu´
o ımedes b) desde
que el hombre es un ser pensante c) desde el descubrimiento
de la rueda
54. ¿Por quien fue publicada la formulaci´n matem´tica?
o a
a) por Isaac Newton b) por Edisson c) por kepler
55. ¿en que a˜o se public´ la formulaci´n matem´tica?
n o o a
a) en 1687 b) en 1234 c) en 1678
56. ¿Qu´ constituye la base de la mecanica clasica?
e
a) las leyes de Newton b) leyes de Keplar c) ley de la gra-
vitaci´n universal
o
57. ¿Qu´ constituye la primera ley de Newton?
e
a) Definici´n de fuerza a causa de la velocidad de los cuer-
o
pos b) A toda acci´n le corresponde una reacci´n c) Todo
o o
lo que sube tiene que bajar
58. ¿Qu´ introduce en fisica, la primera ley de Newton?
e
a) introduce el concepto del sistema de referencia inercial b
)que el cuerpo permanece inerte hasta que es empujado por
una fuerza c) el cuerpo en movimiento mantiene su fuerza
inicial
59. ¿Qu´ es la fuerza?
e
a) es la acci´n mediante la cual cambia el estado de un
o
cuerpo b) es la cantidad de energ´ que agregas a tus mo-
ıa
vimientos c) es cuanta fuerza pones a un aparato

300. 288 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
60. ¿Qu´ mostraron Newton y Galileo?
e
a) que los cuerpos se mueven a velocidad constante y en
l´
ınea recta si no hay fuerzas que act´en sobre ellos b) que
u
la tierra era redonda c) que el universo y los cuerpos tienen
un constante
61. ¿con que otro nombre se le conoce a la segunda ley de New-
ton?
a) ley de la fuerza b)ley de la gravitaci´n universal c)ley de
o
la inercia
62. ¿ que hace la segunda ley de Newton?
a) relaciona las fuerzas actuantes y la variaci´n de la can-
o
tidad de movimiento o momento lineal b)explica como los
cuerpos mantienen una aceleraci´n constante y que solo
o
cambian cuando esta fuerza es detenida. c) que la acelera-
ci´n es constante y que solo los cuerpos en reposo pueden
o
cambiarla.
63. ¿Cu´ndo formul´ Einsten su teor´ de la relatividad?
a o ıa
a) en 1905 b) en 1985 c) en 2005
64. ¿Por qu´ se caracteriza una fuerza?
e
a) por su punto de aplicaci´n, magnitud y su direcci´n b)
o o
por el punto de inclinaci´n y aceleraci´n c) por el punto de
o o
energ´
ıa
65. ¿como se representa una fuerza?
a) por medio de un vector b) por medio magnitud c) por el
punto de inclinacion
66. ¿Como se representa Newton?
a) (N) b) n c) NW

301. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 289
67. ¿como se representa el punto de aplicaci´n?
o
a) (O) b)p. c)p.a
68. ¿Qu´ son las fuerzas no coplanares?
e
a) son Fuerzas que act´an en planos distintos. Los ejes de
u
referencia b) son las fuerzas que no est´n encarreradas c)
a
son fuerzas en el mismo plano pero con diferente valor
69. ¿Qu´ son la fuerzas coplanares?
e
a) Fuerzas que act´an sobre un mismo plano, formado por
u
dos ejes b) Fuerzas que actuan en diferentes planos c) fuer-
zas que act´an paralelamente
u
70. ¿Cu´les son las fuerzas concurrentes?
a
a) Sus rectas de acci´n se cortan en alguna parte en el
o
plano b) Son fuerzas que no tienen punto de interseccion
y que actuan en diferente plano c) son fuerzas que actuan
paralelamente con otras eb diferente plano
71. ¿que son las fuerzas colineales?
a) son las que act´an sobre la misma recta de acci´n b) Son
u o
las que actuan sobre diferente plano c) Son las que act´an
u
sobre una recta paralele con otra
72. ¿Qu´ son las rectas paralelas?
e
a) son dos a mas fuerzas cuyas rectas de acci´n tienen la
o
misma direcci´n b) Son rectas que se intersectan entre si c)
o
son rectas que tienen una distancia determinada
73. ¿Qu´ son las fuerzas puntuales?
e
a) es cuando La superficie sobre la cual act´a Una fuerza es
u
peque˜o en comparaci´n con la superficie total del cuerpo
n o

302. 290 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
Correspondiente. b) Es cuando una superficie liza es relati-
va con la otra c) Es cuando la fuerza de uno es mayor que
otra
74. ¿Qu´ significa fuerza distribuida?
e
a) cuando La superficie o la longitud sobre la cual act´a u
la fuerza es significativa para los c´lculos. b) Es cuando la
a
fuerza se encuentra compacta c) Es la longitud sobre la cual
la aumenta o disminuye la fuerza
75. ¿Qu´ son las fuerzas axiales?
e
a) son fuerzas que act´an a lo largo del eje longitudinal
u
centroidal del Elemento. b) son fuerzas que intersectan en
un punto determinado c) las fuerzas axiales tienen fuerza
propia
76. ¿Qu´ son las fuerzas de atracci´n?
e o
a) tienden a estirar el cuerpo sobre el cual act´an b) Con-
u
traen el cuerpo sobre el cual actuan c) Se atraen una a la
otra
77. ¿Qu´ son las fuerzas de comprensi´n?
e o
a) tienden a acortar o apretar el cuerpo b) tienden a partir
un cuerpo c) atraen los cuerpos
78. ¿Qu´ son las fuerzas flexoras?
e
a) son fuerzas que act´an perpendiculares al eje longitudi-
u
nal centroidal del elemento b) son fuerzas que actuan sobre
un eje en particular c) son fuerzas que actuan sobre un eje
de diferente plano
79. ¿que son las fuerzas torsoras?
a) son las que producen giro alrededor del eje longitudinal

303. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 291
b) son fuerzas que no tienen giro c) son fuerzas que tienen
un giro en direccion contraria al eje
80. ¿ que establece el principio de transmisibilidad?
a) establece que el efecto externo de una fuerza en un cuerpo
r´
ıgido es el mismo para todos los puntos de aplicaci´n a lo
o
largo de su l´
ınea de acci´n b) es cuando tienen las fuerzas
o
actuan a lo largo de eje c) Es la superficie sobre la cual
actuan las fuerzas flexoras
81. ¿Qu´ importancia tiene el rozamiento, en nuestra ´poca?
e e
a) tiene una gran importancia econ´mica b) mucho ya que
o
esta inmerso en nuestro contexto c) genera ingresos
82. ¿con quien comienza el estudio del rozamiento?
a) con Leonardo Da vinci b) con Galileo Galilei c) con Isaac
newton
83. ¿que hizo Leonardo Da Vinci respecto al rozamiento?
a) dedujo las leyes que gobiernan el movimiento de un blo-
que rectangular que desliza sobre una superficie plana b)
dedujo que el movimiento se desliza sobre una base liza c)
dedujo que es imposible tener rozamiento sobre una super-
ficie plana
84. ¿Qui´n redescubri´ las leyes del rozamiento?
e o
a) Galileo y Einstein
b) Pericles
c) El f´
ısico franc´s Guillaume Amontons
e
85. ¿en que siglo se redescubrieron las leyes del rozamiento?
a) en el siglo XVII b) en el siglo XVI c) en el siglo XV

304. 292 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
86. ¿Qu´ otro nombre tiene la primera ley de Newton?
e
a) ley de la inercia b) ley del movimiento de los cuerpos c)
tercera ley de Newton
87. ¿a que se refiere la ley de inercia?
a) nadie hace o deja de hacer algo si no lo obligan b) que
un cuerpo en movimiento puede hacer cambiar a otro c) un
cuerpo solo permanece inerte hasta que se detiene
88. ¿Como se expresa la primera ley de Newton?
a) una part´ıcula libre se mueve con velocidad constante
o sin aceleraci´n b) Una particula solo tiene aceleraci´n
o o
cuando esta en contacto con otra c) una particula libre se
mueve con aceleracion
89. ¿Qu´ son las fuerzas?
e
a) son las cosas responsables de los cambios en el movi-
miento de los cuerpos. b) son los cambios de velocidad c)
son los cambios de longitud
90. ¿que afirma la tercera ley de Newton?
a) afirma que cuando un objeto ejerce una fuerza sobre otro,
este otro objeto ejerce tambi´n una fuerza sobre el primero.
e
b) afirma que cuando un objeto aplica fuerza sobre otro este
permanece inerte c) afirma que un cuerpo permanece inerte
hasta que su longitud cambia
91. ¿Qu´ implica la tercera ley de Newton?
e
a) la conservaci´n del movimiento lineal b) a toda accion
o
corresponde una reaccion c) ley de la conservaci´n de la
o
materia
92. ¿Qu´ es la energ´
e ıa?
a) es la capacidad de un sistema f´
ısico para realizar un

305. 3.2 Trabajo, Potencia y Energ´ Mec´nica.
ıa a 293
trabajo b) es la cantidad de fuerzas ejercida sobre un cuerpo
c) El trabajo que realiza medido por la fuerza
93. ¿que hizo James Prescott Joule?
a) centr´ sus investigaciones en los campos de la electricidad
o
y termodin´mica b) gran astronomo italiano c) utilizo la
a
bombilla como uno de sus inventos mas importantes
94. ¿Qu´ demostr´ Joule?
e o
a) demostr´ que el calor es una transferencia de energ´ b)
o ıa
que la transferencia de energia solo se puede realizar con un
cuerpo igual c) que la energia es una transferencia de calor
95. ¿Qu´ determin´ Joule?
e o
a) el equivalente mec´nico del calor b) el equivalente de la
a
energ´ c) el equivalente de la mecanica
ıa
96. ¿Como se traduce al espa˜ol la cantidad “Joule”?
n
a) se traduce como julio b) Se traduce como Julieta c) se
traduce como juy
97. ¿Qu´ es un joule?
e
a) el el trabajo realizado por una fuerza [N], aplicada para
Producir un desplazamiento [m]. b) Es el trabajo que se
realiza sin desplazamiento c) Es el trabajo que se realiza
con un desplazamiento irregular
98. ¿Qu´ mide la potencia?
e
a) Mide la rapidez con que se realiza un trabajo. b) mide
la energia de una cuerpo c) mide el trabajo que tiene un
cuerpo
99. En t´rminos matem´ticos ... ¿Qu´ es la potencia?
e a e
a) es igual al trabajo realizado dividido entre el intervalo

306. 294 Leyes de Newton, Trabajo, Potencia y Energ´
ıa
de tiempo a lo largo del cual se efect´a el trabajo b) Es
u
el producto de l trabajo realizado por un cuerpo en reposo
y uno en movimiento c) Es el intervalo realiza entre dos
cuerpos
100. ¿Qu´ es inercia?
e
a) Propiedad de los cuerpos de no modificar su estado de
reposo o movimiento si no es por la acci´n de una fuerza.
o
b) Es cuando un cuerpo permanece en movimiento c) Es
cuando un cuerpo permane en movimiento y es capas de
modificar su estado
101. ¿Cuando no se realiza un trabajo?
a) Cuando se ejerce una fuerza sobre un objeto pero la fuer-
za no hace que el objeto se mueva. b) Es cuando dos cuerpos
intercambian energ´ c) Cuando se ejerce una fuerza a un
ıa
objeto y este reacciona.

307. Bibliograf´
ıa

308. 296 Bibliograf´
ıa
´
BASICA:

309. Bibliograf´
ıa
[1] Competencias Gen´ricas y el perfil del egresado de la Educa-
e
ci´n media Superior. SEP SEMS Enero 2008.
o
[2] Hewitt, Paul G.F´sica Conceptual. M´xico, 9a. Ed., Pearson
ı e
Educaci´n, 2004.
o
[3] P´rez Montiel, H´ctor. F´sica 2 para Bachillerato General.
e e ı
a
M´xico, 2 . Ed., Publicaciones Cultural, 2003.
e
[4] Tippens, Paul, E. F´sica, Conceptos y Aplicaciones. M´xico,
ı e
a
6 . Ed., McGraw - Hill, 2001.
COMPLEMENTARIA
[5] Resnick, Robert; Halliday, David; Krane, Kenneth S F´sica,
ı
edit. CECSA (1993)
[6] Giancoli, Douglas C. F´sica y aplicaciones. M´xico, 4a . Ed.,
ı e
Prentice Hall, 1999.
[7] Hetch, Eugene. F´sica, Algebra y Trigonometr´a. M´xico,
ı ı e
Ed., Thompson, 1999.
[8] P´rez Montiel, H´ctor. F´sica General. M´xico, 3a . Ed., Pu-
e e ı e
blicaciones Cultural, 2006.
[9] Serway, Raymond A F´sica, edit. Interamericana, M´xico
ı e
(1985).

310. 298 BIBLIOGRAF´
IA
[10] Serway, Raymond A. F´sica Tomo 1. M´xico, 4a. Ed., Mc-
ı e
Graw - Hill, 1996.
[11] ·Tipler, Paul A. F´sica edit. Revert´, Barcelona (1978).
ı e
[12] Wilson, Jerry D. F´sica. M´xico, 2a. Ed., Pearson Educa-
ı e
ci´n, 1996.
o
[13] Alonso Marcelo, Finn Edward J. F´sica I. Editorial Fondo
ı
Educativo Interamericano, M´xico, 1976.
e
[14] F. W. Sears & M. W. Zemansky F´sica General ed. Aguilar
ı
trad de la 2a ed. de A. Y. Almarza
[15] Fernand P. Beer, G. Bussell Johnstar Jr. Mec´nica Vectorial
a
para Ingenieros 5ta. Edici´n Mc. Graw Hill, M´xico, 1996
o e
[16] Howard P. Burns & Joseph Birch Mechanics Manual 4th
edition.
[17] McCliment, Edward R. Physics, edit: Harcourt Brace Jova-
novich, Publishers, San Diego (1984)
[18] Wolfson, Richard; Pasachoff, Jay M. Physics edit: Little,
Brown and Company, Boston (1987).
[19] Facorro L. A Hidr´ulica, edit. Alsina, Buenos Aires (1960).
a
[20] Koshkin, Shirk´vich. Manual de F´sica Elemental. Editorial
e ı
Mir 1975.
[21] Irene Cruz G., A. Nosnik, Elsa Recillas El Hombre de la
Torre Inclinada. Editorial Pangea/Conacyt M´xico 1985.
e

311. BIBLIOGRAF´
IA 299
[22] B., Swam. El Ingl´s de la Manzana. Editorial Pan-
e
gea/Conacyt M´xico 1986.
e
[23] D´niz S., A. Gonz´lez S., M.Introducci´n en la Teor´a de
e a o ı
Errores, J ULPGC
[24] D´niz S., A. Gonz´lez S., M. Medidas de Longitudes J
e a
ULPGC
[25] D´niz S., A. Gonz´lez S., M. Cuaderno No 1. C´lculos Ba-
e a a
sados en Medidas de Longitud, J ULPGC.
ılia. Proyecto: Water Rocket.
[26] Barreiro, P. O. Romanelli, L´
http://www.ungs.edu.ar/ici/fisica/fisica1/cohete/
[27] Gran Diccionario Enciclop´dico Ilustrado ESPASA Espa˜a
e n
1998
REVISTAS
[28] Reed B. C. Archimedes’ law sets a good energy-
minimization example. Physics Education, 39 (4) July 2004,
pp. 322-323.
[29] Keeports D. How does the potencial energy of a rising
helium-filled balloon change?. The Physics Teacher, Vol 40,
March 2002, pp. 164-165.
[30] Silva A., Archimedes’ law and the potential energy: mode-
lling and simulation with a sreadsheet. Phys. Educ. 33 (2)
March 1998. pp. 87-92.
[31] Bierman J, Kincanon E. Reconsidering Archimedes’ prin-
ciple. The Physics Teacher, Vol 41, Setember 2003, pp.
340-344.
´
PAGINAS DE INTERNET

312. 300 BIBLIOGRAF´
IA
[32] http://www.monografias.com
[33] http://www.eng.iastate.edu/efmd/statics.htm#mecanics
[34] http://www.ual.es/aposadas/08 Estatica.pdf
[35] http://www.fisica.usach.cl/—didactic/estatica murrieta.pdf
[36] http://www.fisicanet.fateback.com/materias/f1/f1 1/estatica.html-
6k
[37] http://www.edu.aytolacoruna.es/aula/fisica/teoria/A Franco/problemas/
ca.htm
[38] http://www.mec.puc-rio.br/prof/dreux/estatica.htm/
[39] http://www.ociv.utfsm.cl/docencia/academicos/Estatica Estructuras/files
[40] http://www.ualg.pt/-rlanca/sebenta fisica/02 aulateorica estatica das par
[41] http://www.newton.cnice.es/4eso/est´tica/estatica4.htm
a
[42] http://www.virtual.unaledu.co/cursos/ingenieria/2001734/
[43] www.geocities.com/gsilvam/hidro.htm
[44] www.monografias.com/trabjos10/hidra/hidra.shtml
[45] www.es.wikipedia.org/wiki/
[46] Biblioteca de Consulta Microsoft R Encarta R 2005. c
1993-2004 Microsoft Corporation. Reservados todos los dere-
chos.

313. Ap´ndices
e

314. 302 Ap´ndice B: Funciones y Gr´ficas
e a
6.1. Apendice A: Respuestas a Preguntas y
Ejercicios
1.1Generalidades
1.a 2a 3b 4a 5c 6a 7b 8a 9c 10 b
1.1.1 La F´
ısica y su Impacto en la Ciencia y la Tecnolog´
ıa
1a 2 a 3a 4b 5c 6a 7a 8a 9b 10b
1.1.2 Los M´todos de Investigaci´n y su Relevancia en el
e o
Desarrollo de la Ciencia
1a 2b 3b 4 b 3c 5c 6 a 7 a 8 a 9b 10 c
1.2 Magnitudes F´ ısicas y su Medici´n
o
1a 2c 3b 4 a 5 a 6 a 7a a 9 a 10 b
1.2.1 Magnitudes Fundamentales y Derivadas
1a2aba3a4a5a
6.2. Apendice B: Funciones y Gr´ficas
a
En las ciencias existen relaciones entre cantidades a las que
se les llama variables, porque pueden tomar diferentes valores.
Estas varibles, forman una figura en el papel si en los ejes de
coordenadas, se dibujan sus valores, asignando a cada una un
eje para que se pueda representar.
La figura obtenida , se conoce como g´fica de la funci´n.
a o
Variables: Cantidades sin un valor definido se representan por
letras. Por su tipo, pueden ser dependientes e independientes. A
la que se encuentra en el lado izquierdo del signo igual, se le
conoce como variable dependiente las que se encuentran a la
derecha del signo igual, se les conoce como variables indepen-
dientes y puede se una combinaci´n de t´rminos con exponentes
o e
y o sin ellos adem´s de cantidades “ constantes” cuyo valor no
a
cambia..

315. Ap´ndice B
e 303
Figura 6.1: Funci´n Lineal y = k
o
A las variables independientes se acostumbra darles valores
y obtener as´ el valor de la variable dependiente.
ı
Funciones Elementales
Funciones:
1. constante:
y=k (6.1)
2. Lineal:
y = kx (6.2)
3. Lineal desplazada:
y = ax + b (6.3)

316. 304 Ap´ndice B: Funciones y Gr´ficas
e a
Figura 6.2: Funci´n Lineal y = kx
o
Figura 6.3: Funci´n Lineal y = kx + b
o

317. Ap´ndice B
e 305
Figura 6.4: Funci´n Cuadr´tica y = x2
o a
4. Cuadr´tica: Par´bola
a a
y = ax2 + bx + c (6.4)
5. Inversa: Hip´rbola
e
1
y=k (6.5)
x
6. Inversa cuadr´tica:
a
1
y=k (6.6)
x2
Existen otros tipos de funciones, pero para el prop´sito de
o
estos apuntes, solo se tratar´n estas.
a

318. 306 Ap´ndice B: Funciones y Gr´ficas
e a
1
Figura 6.5: Funci´n Inversa y =
o x
1
Figura 6.6: Funci´n Inversa Cuadr´tica y =
o a x2

319. 6.3 Apendice C: Tipos de Proporcionalidad 307
6.3. Apendice C: Tipos de Proporcionali-
dad
proporcionalidad:
1. Directa:
Se obtiene cuando de dos columnas de valores,
a). Los valores en ambas, aumentan o disminuyen
b). Cuando los valores se grafican, se obtiene una funcion
lineal ecuaciones:(6.2) o (6.3)
c). Al dividir el valor de la variable dependiente entre el
valor de la independiente, se obtiene un valor igual,
este se conoce como “ Constante de proporcionalidad
”.
Proporcionalidad Directa con el Cuadrado:
2. a). Los valores en ambas, aumentan o disminuyen
b). Cuando los valores se grafican, se obtiene una funcion
cuadr´tica ecuacion:(6.4)
a
c). Al dividir el valor de la variable dependiente entre el
valor de la independiente elevada al cuadrado, se ob-
tiene un valor igual, este se conoce como “Constante
de proporcionalidad”.

320. 308 Ap´ndice C: Tipos de Proporcionalidad
e
3. Proporcionalidad Inversa:
a). Los valores en una columna, aumentan y en la otra
disminuyen o al contrario.
b). Cuando los valores se grafican, se obtiene una funcion
inversa ecuacion:(6.5)
c). Al multiplicar el valor de la variable dependiente entre
el valor de la independiente elevada al cuadrado, se
obtiene un valor igual, este se conoce como “Constante
de proporcionalidad”.
Proporcionalidad Inversa con el Cuadrado
4. a). Los valores en una columna, aumentan y en la otra
disminuyen o al contrario.
b). Cuando los valores se grafican, se obtiene una funcion
cuadr´tica inversa ecuacion:(6.6)
a
c). Al multiplicar el valor de la variable dependiente por
el valor de la independiente elevada al cuadrado, se
obtiene un valor igual, este se conoce como “Constante
de proporcionalidad”.

321. ´
Indice alfab´tico
e
ciencia leyes de newton, 205
definici´n, 27
o fuerza, 205
cinem´tica
a fuerzas de fricci´n, 212
o
conceptos fundamentales, 122 origen, 213
la Gravitaci´n Universal, 240
o
energ´ 254
ıa,
masa gravitacional e inercial,
cin´tica, 256
e
221
conservaci´n de la, 257
o
peso, 221
potencial, 254
peso de los cuerpos, 209
errores
primera ley, 215
reglas, 86
segunda ley, 218
tipos, 81
tercera ley, 238
F´ısica leyes Kepler, 242
definici´n, 27
o
m´todo cient´
e ıfico, 41
divisi´n, 28
o
macromundo, 39
historia, 8
magnitudes
impacto de la, 41
fundamentales y derivadas,
Fen´meno, 37
o
48
biol´gico, 37
o
medici´n, 45
o
F´ ısico, 37
materia
Qu´ ımico, 37
propiedades, 30
impulso y cantidad de movimien- medici´n, 48
o
to, 260 metodos de, 56
conservaci´n del, 264
o directa, 56

322. 310 ´ ´
INDICE ALFABETICO
indirecta, 56 relativo, 122
medir, 48 sistema de coordenadas, 124
metodo cient´ ıfico, 41 sistema de referencia, 122
micromundo, 38 sistema de referencia iner-
movimiento cial, 123
aceleraci´n, 150
o sistema de referencia no iner-
circular, 182 cial, 123
aceleraci´n centr´
o ıpeta, 190 tiro horizontal, 169
uniforme, 184 trayectoria, 126
uniforme acelerado, 195 velocidad, 130
velocidad angular, 186 instantanea, 134
desplazamiento, 127 promedio, 133
distancia, 126
notaci´n base 10, 56
o
en dos dimensiones, 168
gr´ficas, 135
a potencia, 250
MUA procedimiento
casos, 159 dibujo de vectores, 98
ejemplos, 153
posici´n final, 151
o sistemas de unidades, 50
tiro vertical, 159 CGS, 50
velocidad final, 151 ingl´s, 51
e
parab´lico, 173
o SI, 51
posici´n, 126
o ventajas y limitaciones, 53
rapidez, 131 transformaci´n entre, 59
o
rectil´
ıneo uniforme acelera- tecnolog´ 41
ıa,
do trabajo, 249
ecuaciones, 153
rectil´
ıneo uniforme acelera- vectores, 91
do (MUA), 150 caracter´ısticas, 93
rectilineo uniforme, 129 descomposici´n de, 99
o

323. ´ ´
INDICE ALFABETICO 311
magnitudes escalares y vec-
toriales, 91
notaci´n, 94
o
principio de transmisibilidad,
97
representaci´n, 93
o
representaci´n gr´fica, 95
o a
resta de, 104
suma de, 101
m´todo del pol´
e ıgono, 105
teorema de Pit´goras, 109
a
unitarios, 113