Este documento presenta los conceptos básicos sobre funciones, incluyendo su definición, dominio, imagen y gráfica. Explica características como la composición de funciones e inversa de una función. Finalmente, detalla el estudio de funciones elementales como polinómicas, racionales e irracionales.



![Conceptos básicos sobre funciones
Algunas características sobre funciones
Composición de funciones
Inversa de una función
Estudio de las funciones elementales
Función real de variable real
Definición
Sea D un subconjunto de números reales. Una función es una “ley”
que a cada número real x del subconjunto D le asocia otro número
real único (denominado imagen de x). Al conjunto D se le llama
dominio de la función.
Ejemplos
1 A cada número no negativo se le asocia su raíz cuadrada
positiva
2 A cada número del intervalo [-1,5] se le asocia su cuadrado
aumentado en dos unidades
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-6-320.jpg)
![Conceptos básicos sobre funciones
Algunas características sobre funciones
Composición de funciones
Inversa de una función
Estudio de las funciones elementales
Función real de variable real
Definición
Sea D un subconjunto de números reales. Una función es una “ley”
que a cada número real x del subconjunto D le asocia otro número
real único (denominado imagen de x). Al conjunto D se le llama
dominio de la función.
Ejemplos
1 A cada número no negativo se le asocia su raíz cuadrada
positiva
2 A cada número del intervalo [-1,5] se le asocia su cuadrado
aumentado en dos unidades
3 A cada número distinto de 0 se le asocia su inverso
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-7-320.jpg)





![Conceptos básicos sobre funciones
Algunas características sobre funciones
Composición de funciones
Inversa de una función
Estudio de las funciones elementales
Función real de variable real
f: D −→ R
x → f (x)
Ejemplos
1 A cada número no negativo se le asocia su raíz cuadrada
positiva
f : R+ ∪ {0} −→ R√
x −→ + x
2 A cada número del intervalo [-1,5] se le asocia su cuadrado
aumentado en dos unidades
g : [−1, 5] −→ R
x −→ x 2 + 2
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-13-320.jpg)
![Conceptos básicos sobre funciones
Algunas características sobre funciones
Composición de funciones
Inversa de una función
Estudio de las funciones elementales
Función real de variable real
f: D −→ R
x → f (x)
Ejemplos
1 A cada número no negativo se le asocia su raíz cuadrada
positiva
f : R+ ∪ {0} −→ R√
x −→ + x
2 A cada número del intervalo [-1,5] se le asocia su cuadrado
aumentado en dos unidades
g : [−1, 5] −→ R
x −→ x 2 + 2
3 A cada número distinto de 0 se le asocia su inverso
h : R{0} −→ R
x −→ 1/x
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-14-320.jpg)






















![Conceptos básicos sobre funciones
Algunas características sobre funciones
Composición de funciones
Inversa de una función
Estudio de las funciones elementales
Acotación
f(x)=x2+1 en [−2,2]
40
35
30
25
20
15
10
5
0
−6 −4 −2 0 2 4 6
La función f (x) = x 2 + 1 en [-2,2]:
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-42-320.jpg)
![Conceptos básicos sobre funciones
Algunas características sobre funciones
Composición de funciones
Inversa de una función
Estudio de las funciones elementales
Acotación
f(x)=x2+1 en [−2,2]
40
35
30
25
20
15
10
5
0
−6 −4 −2 0 2 4 6
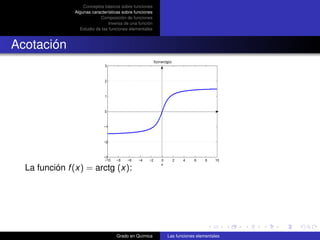
La función f (x) = x 2 + 1 en [-2,2]:
está acotada superiormente (M = 5 es cota superior)
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-43-320.jpg)
![Conceptos básicos sobre funciones
Algunas características sobre funciones
Composición de funciones
Inversa de una función
Estudio de las funciones elementales
Acotación
f(x)=x2+1 en [−2,2]
40
35
30
25
20
15
10
5
0
−6 −4 −2 0 2 4 6
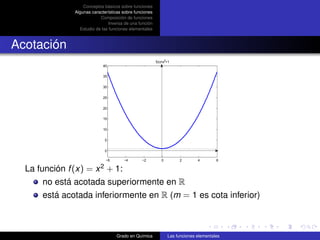
La función f (x) = x 2 + 1 en [-2,2]:
está acotada superiormente (M = 5 es cota superior)
está acotada inferiormente (m = 1 es cota inferior)
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-44-320.jpg)






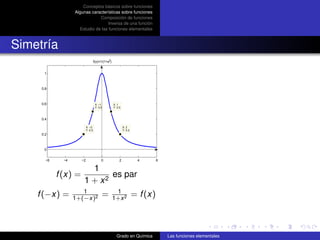



























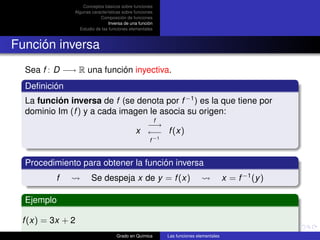



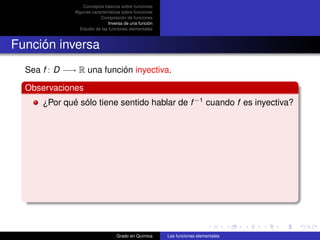



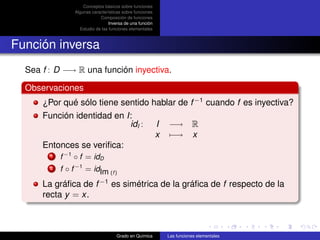

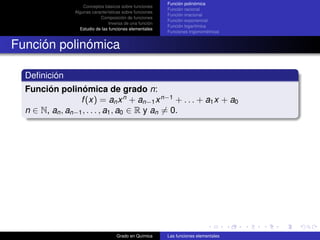



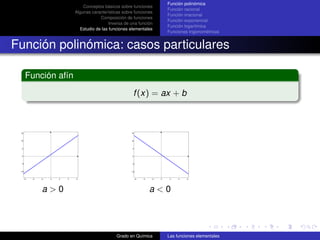







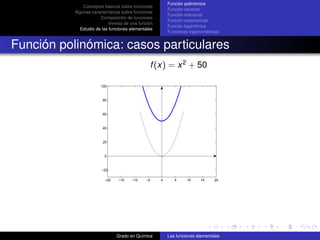
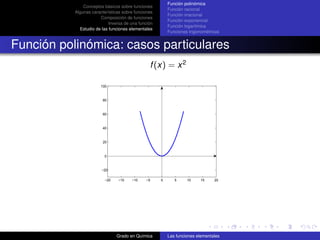


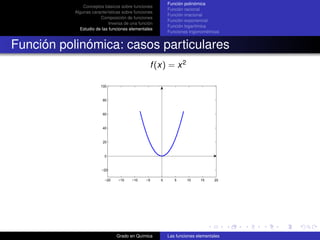
































![Función polinómica
Conceptos básicos sobre funciones
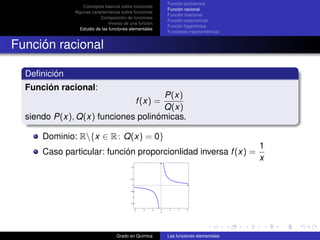
Función racional
Algunas características sobre funciones
Función irracional
Composición de funciones
Función exponencial
Inversa de una función
Función logarítmica
Estudio de las funciones elementales
Funciones trigonométricas
Función seno
Definición
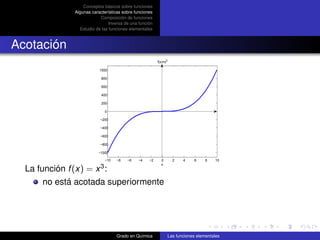
Función seno:
f (x) = sen x x en radianes
Dominio: R
Imagen: [−1, 1]
Periódica de periodo 2π
Impar: sen (−x) = −sen x
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-145-320.jpg)
![Función polinómica
Conceptos básicos sobre funciones
Función racional
Algunas características sobre funciones
Función irracional
Composición de funciones
Función exponencial
Inversa de una función
Función logarítmica
Estudio de las funciones elementales
Funciones trigonométricas
Función seno
Definición
Función seno:
f (x) = sen x x en radianes
f(x)=sen(x)
2
Dominio: R 1.5
1
Imagen: [−1, 1] 0.5
Periódica de periodo 2π 0
Impar: sen (−x) = −sen x −0.5
−1
−1.5
−2
−20 −15 −10 −5 0 5 10 15 20
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-146-320.jpg)

![Función polinómica
Conceptos básicos sobre funciones
Función racional
Algunas características sobre funciones
Función irracional
Composición de funciones
Función exponencial
Inversa de una función
Función logarítmica
Estudio de las funciones elementales
Funciones trigonométricas
Función coseno
Definición
Función coseno:
f (x) = cos x x en radianes
Dominio: R
Imagen: [−1, 1]
Periódica de periodo 2π
Par: cos (−x) = cos x
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-148-320.jpg)
![Función polinómica
Conceptos básicos sobre funciones
Función racional
Algunas características sobre funciones
Función irracional
Composición de funciones
Función exponencial
Inversa de una función
Función logarítmica
Estudio de las funciones elementales
Funciones trigonométricas
Función coseno
Definición
Función coseno:
f (x) = cos x x en radianes
f(x)=cos x
2
Dominio: R 1.5
1
Imagen: [−1, 1] 0.5
Periódica de periodo 2π 0
Par: cos (−x) = cos x −0.5
−1
−1.5
−2
−20 −15 −10 −5 0 5 10 15 20
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-149-320.jpg)






![Función polinómica
Conceptos básicos sobre funciones
Función racional
Algunas características sobre funciones
Función irracional
Composición de funciones
Función exponencial
Inversa de una función
Función logarítmica
Estudio de las funciones elementales
Funciones trigonométricas
Función arco seno
Definición
Función arco seno:
f (x) = arc sen x
f(x)=arc sen x
1.5
1
0.5
Dominio: [−1, 1] 0
π π
Imagen: − , −0.5
2 2
−1
−1.5
−1.5 −1 −0.5 0 0.5 1 1.5
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-156-320.jpg)


![Función polinómica
Conceptos básicos sobre funciones
Función racional
Algunas características sobre funciones
Función irracional
Composición de funciones
Función exponencial
Inversa de una función
Función logarítmica
Estudio de las funciones elementales
Funciones trigonométricas
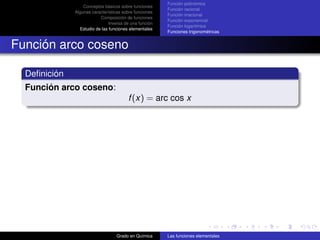
Función arco coseno
Definición
Función arco coseno:
f (x) = arc cos x
f(x)=arc cos x
3
2.5
2
1.5
Dominio: [−1, 1] 1
Imagen: [0, π] 0.5
0
−0.5
−1
−1 −0.5 0 0.5 1 1.5 2 2.5 3
Grado en Química Las funciones elementales](https://image.slidesharecdn.com/funciones-091210123121-phpapp01/85/Funciones-160-320.jpg)



