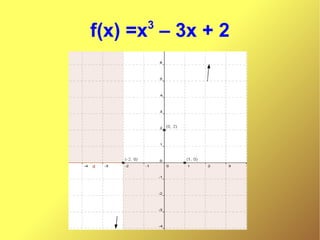
Este documento resume las propiedades de la función f(x) = x3 - 3x + 2. El dominio es el conjunto de los números reales. Los puntos de corte con los ejes son (-2,0), (1,0) y (0,2). No hay asíntotas. Los puntos críticos son -1 y 1, siendo (-1,4) un máximo relativo y (1,0) un mínimo relativo. El punto de inflexión es (0,2).

1. 3
f(x) =x – 3x + 2
1º Dominio
Todos los números reales por ser un polinomio.
Por tanto, no se descarta ninguna zona.

2. 3
f(x) =x – 3x + 2

3. 3
f(x) =x – 3x + 2
2º Cortes con los ejes y signo
Corte eje OX : y = 0. x3 – 3x + 2 = 0
Resolvemos por Ruffini la ecuación y sale de solución x = -2, x = 1 y x = 1
Luego los puntos de corte con el eje OX son: (-2,0) y (1,0)
Corte eje Y: x = 0 f(0) = 2
Luego el punto de corte con el eje es: (0,2)
- + +
Signo de
f(x) -2 1

4. 3
f(x) =x – 3x + 2

5. 3
f(x) =x – 3x + 2
3º Asíntotas y ramas infinitas
A. Vertical: No puede haber por tratarse de un polinomio
A. Horizontal:
lim f ( x)=+ ∞ lim f ( x)=−∞
x →+ ∞ x →−∞
No hay asíntotas horizontales
A. Oblicua:
f ( x) f ( x)
lim =+ ∞ lim =−∞
x →+ ∞ x x → −∞ x
No hay asíntotas oblicuas

6. 3
f(x) =x – 3x + 2

7. 3
f(x) =x – 3x + 2
4º: Monotonía
f '(x) = 3x2 – 3 3X2 – 3 = 0
X = 1 y x = -1

8. 3
f(x) =x – 3x + 2
4º: Monotonía
f '(x) = 3x2 – 3 3X2 – 3 = 0
X = 1 y x = -1
+ - +
Signo de
f ' (x) -1 1
Máximo Mínimo
relativo relativo
f(-1) = 4 f(1)=0
(-1 , 4) (1 , 0)

9. 3
f(x) =x – 3x + 2

10. 3
f(x) =x – 3x + 2
5º: Curvatura
f '(x) = 3x2 – 3
f '' (x) = 6x 6x = 0 X=0

11. 3
f(x) =x – 3x + 2
5º: Curvatura
f '(x) = 3x2 – 3
f '' (x) = 6x 6x = 0 X=0
- +
Signo
f '' (x)
0
X = 0 es punto de
inflexión
f(0) = 2 (0 , 2)

12. 3
f(x) =x – 3x + 2

13. 3
f(x) =x – 3x + 2