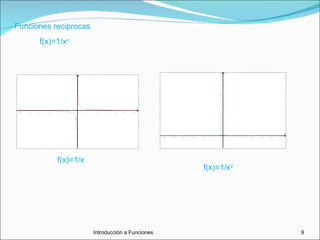
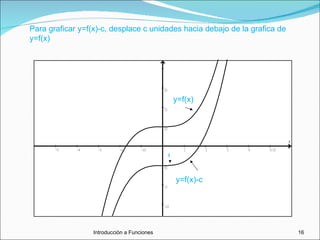
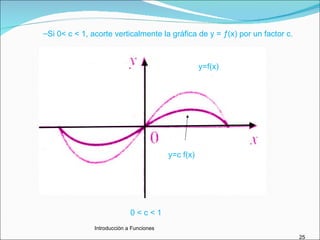
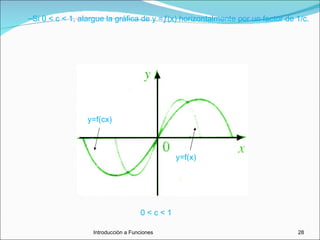
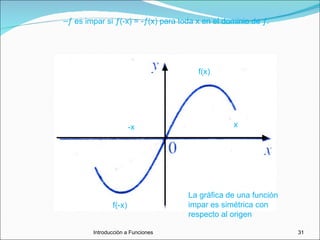
Este documento trata sobre funciones. Explica qué es una función y cómo se pueden representar funciones de manera verbal, algebraica, gráfica y numérica. También describe gráficas de funciones, funciones crecientes y decrecientes, transformaciones de funciones como desplazamientos y reflexiones, y conceptos como funciones cuadráticas, máximos y mínimos, modelado con funciones, composición e inversión de funciones.

1. FUNCIONES ¿Qué es una función? Gráficas de funciones Funciones crecientes y decrecientes; tasa de cambio promedio Transformaciones de funciones Funciones cuadráticas; máximos y mínimos Modelado con funciones Combinación de funciones Funciones uno a uno y sus inversas Introducciòn a Funciones

2. ¿Qué es una función? Una función f es una regla que asigna a cada elemento, llamado f(x), en un conjunto B . Introducciòn a Funciones

3. Cuatro formas de representar una función 2 Introducciòn a Funciones W(onzaS) C(w) dólares 0 <w<_1 0.37 Verbal: Con palabras: P(t) es la “población del mundo en el instante t ” Algebraicamente: Por medio de una fórmula: A(r)= π r Visual: Por medio de una gráfica: Numérica: Por medio de una tabla de valores:

4. GRAFICA DE UNA FUNCIÒN Si f es una función con dominio A, entonces la gráfica de f es el conjunto de pares ordenados {( x.ƒ(x))|xє A } En otras palabras, la gráfica de ƒ es el conjunto de los puntos (x,y) tales que y= ƒ(x); es decir, la gráfica de la ecuación y = ƒ(x). La gráfica de una función ƒ da un cuadro del comportamiento o “historia de vida” de la función. Se puede leer el valor de ƒ (x) de la gráfica como la altura de la gráfica arriba del punto x. Una función ƒ de la forma ƒ(x) = mx + b se llama función lineal por que su gráfica es de la ecuación y = mx + b, que representa una recta con pendiente m y ordenada al origen b. Un caso especial de una función lineal se presenta cuando la pendiente m = 0. La función ƒ(x) = b, donde b es un determinado número. Se llama función constante porque todos sus valores horizontal y= b son el mismo número, a saber, b. Su gráfica es la recta . F(x)=3 F(x)=2x+1 Introducciòn a Funciones

5. PRUEBA DE LA LÍNEA VERTICAL Una curva en el plano coordenado es la gráfica de una función si y sólo si ninguna línea vertical corta la curva más de una vez. Introducciòn a Funciones

6. ALGUNAS FUNCIONES Y SUS GRÁFICAS F(x)=b F(x)=mx+b Funciones lineales F(x)=mx+b Introducciòn a Funciones

7. Funciones exponenciales f(x)=x n F(x)=x 2 f(x)=x 3 f(x)=x 4 f(x)=x 5 Introducciòn a Funciones

8. Funciones de raíz f(x)= n F(x)=(x) ^(1/2) f(x)=(x) ^(1/3) f(x)=(x) ^(1/5) f(x)=(x) ^(1/4) Introducciòn a Funciones

9. Funciones reciprocas f(x)=1/x n f(x)=1/x f(x)=1/x 2 Introducciòn a Funciones

10. Función valor absoluto f(x)=|x| Función entero máximo Introducciòn a Funciones

11. DEFINICIÒN DE FUNCIONES CRECIENTES Y DECRECIENTES ƒ Es creciente en un intervalo I si ƒ(x1) < ƒ(x2) siempre que x1 < x2 en I. ƒ Es decreciente en un intervalo I si ƒ(x1) > ƒ(x) siempre que x1 > x2 en I . Introducciòn a Funciones

12. TASA DE CAMBIO PROMEDIO La tasa de cambio de promedio de la función y=ƒ(x) entre x= a y x= b es = Cambio en y Cambio en x = ƒ(b)- ƒ(a) b - a tasa de promedio Introducciòn a Funciones

13. f(a) f(b) b-a f(b)-f(a ) y=f(x) a b La tasa de cambio de promedio es la pendiente de la recta secante entre x= ay x=b en la gráfica de ƒ, es decir, la recta que pasa por (a.ƒ(a)) y (b.ƒ(b)). Introducciòn a Funciones

14. TRANSFORMACIÒN DE FUNCIONES DESPLAZAMIENTOS VERTICALES DE GRÁFICAS Sumar una constante a una función desplaza su gráfica en dirección vertical: hacia arriba si la constante es positiva y hacia abajo si la constante es negativa Introducciòn a Funciones

15. Suponga que c > 0. Para gráficas y = ƒ(x) + c, desplace c unidades hacia arriba la gráfica de y = ƒ(x). c y=f(x)+c y=f(x) Introducciòn a Funciones

16. Para graficar y=f(x)-c, desplace c unidades hacia debajo de la grafica de y=f(x) c y=f(x)-c y=f(x) Introducciòn a Funciones

17. DESPLAZAMIENTOS HORIZONTALES DE GRÁFICAS Introducciòn a Funciones

18. y=f(x) c y=f(x-c) a) Para graficar y = ƒ(x – c), desplace la gráfica de y = ƒ(x) a la derecha c unidades. Supóngase que c > 0. Introducciòn a Funciones

19. c y=f(x+c) y=f(x) b) Para graficar y = ƒ(x + c), desplace la gráfica de y = ƒ(x) a la izquierda c unidades. Introducciòn a Funciones

20. REFLEXIÓN DE GRÁFICAS Introducciòn a Funciones

21. Para graficar y = -ƒ(x), refleje la gráfica de y = ƒ(x) en el eje x. Introducciòn a Funciones

22. Para graficar y = ƒ(-x), refleje la gráfica de y = ƒ(x) en el eje y. Introducciòn a Funciones

23. Estiramiento y acortamiento vertical de gráficas Introducciòn a Funciones

24. Si c > 1, alargue verticalmente la gráfica de y =ƒ(x) por un factor de c. c>1 y=f(x) y=c f(x) Para graficar y = c ƒ(x): Introducciòn a Funciones

25. Si 0< c < 1, acorte verticalmente la gráfica de y = ƒ(x) por un factor c. 0 < c < 1 y=c f(x) y=f(x) Introducciòn a Funciones

26. Acortamiento y alargamiento horizontal de gráficas Introducciòn a Funciones

27. Si c > 1,acorte la gráfica de y = ƒ(x) horizontalmente por un factor del 1/c. y=f(cx) y=f(x) c > 1 La gráfica de y = ƒ(cx): Introducciòn a Funciones

28. Si 0 < c < 1, alargue la gráfica de y =ƒ(x) horizontalmente por un factor de 1/c. y=f(x) y=f(cx) 0 < c < 1 Introducciòn a Funciones

29. FUNCIONES PAR E IMPAR Introducciòn a Funciones

30. ƒ es par si ƒ(-x) = ƒ(x) para toda x en el dominio de ƒ. f-(x) f(x) -x x La gráfica de una función par es simétrica con respecto al eje y Sea ƒ una función. Introducciòn a Funciones

31. ƒ es impar si ƒ(-x) = -ƒ(x) para toda x en el dominio de ƒ. -x x f(-x) f(x) La gráfica de una función impar es simétrica con respecto al origen Introducciòn a Funciones

32. FUNCIONES CUADRATICAS; MÁXIMOS Y MINIMOS Un valor máximo o mínimo de una función es el valor más grande o más pequeño de la función en un intervalo. Para una función que representa la ganancia de un negocio, se estaría interesado en el valor máximo: para una función que representa la cantidad de material en un proceso de manufactura, se estaría interesando en el valor mínimo. Introducciòn a Funciones

33. FORMA ESTÁNDAR DE UNA FUNCIÓN CUADRÁTICA Una función cuadrática ƒ(x) = ax + bx + c se puede expresar en la forma estándar ƒ(x) = a(x – h) + k complementando el cuadrado. La gráfica de ƒ es una parábola con vértice (h,k); la parábola se abre hacia arriba si a < 0. 2 2 2 f(x)=a (x-h) +k, a > 0 2 f(x)=a (x-h) +k, a<0 2 Vértice (h, k) Vértice (h, k) Introducciòn a Funciones

34. VALOR MÁXIMO O MÍNIMO DE UNA FUNCIÓN CUADRÁTICA Sea ƒ una función cuadrática con forma estándar ƒ(x) = a(x – h) + k. El valor máximo o mínimo de ƒ ocurre en x = h. Si a > 0, entonces el valor mínimo de ƒ(h) = k. Si a < 0, entonces el valor máximo de ƒ(h) = k. 2 f(x)=a (x-h) 0+k, a > f(x)=a (x-h) <0+k, a 2 2 Mínimo Máximo Introducciòn a Funciones

35. VALOR MÁXIMO O MÍNIMO DE UNA FUNCIÓN CUADRÁTICA El valor máximo o mínimo de una función cuadrática ƒ(x) = ax + bx + c ocurre en: x=-b/2ª Si a > 0, entonces el valor mínimo es ƒ(-b/2a). Si a < 0, entonces el valor máximo es ƒ(-b/2a). Introducciòn a Funciones

36. MODELADO CON FUNCIONES Muchos de los procesos estudiados en las ciencias físicas y sociales requieren entender como varían una cantidad respecto a otra. Hallar una función que describe la dependencia de una cantidad en otra se llama modelado. Introducciòn a Funciones

37. NORMAS PARA MODELAR CON FUNCIONES 1. Exprese el modelo en palabras. Identifique la cantidad que quiere modelar y exprésela, en palabras, como una función de otras cantidades en el problema. 2. Elija la variable. Identifique las variables empleadas para expresar la función en el paso 1. asigne un símbolo, como x , a una variable y exprese las otras variables en términos de este símbolo. 3. Establezca el modelo. Exprese la función en el lenguaje del álgebra al escribirla como una función de la única variable elegida en el paso 2. 4. Use el modelo. Emplee la función para contestar las preguntas planteadas en el problema. Introducciòn a Funciones

38. COMBINACIÓN DE FUNCIONES ÁLGEBRA DE FUNCIONES Sean ƒ y g funciones con dominios A y B. Entonces las funciones ƒ + g, ƒ – g, ƒg y ƒ/g se define como sigue. ( ƒ + g)(x) = ƒ(x) + g(x) Dominio A B (ƒ – g)(x) = ƒ(x) – g(x) Dominio A B (ƒg)(x) = ƒ(x)g(x) Dominio A B ( ƒ/g) (x) = ƒ(x)g(x)/g(x) Dominio {x Є A B І g = 0 } υ υ υ υ Introducciòn a Funciones

39. COMPOSICIÓN DE FUNCIONES Dada dos funciones ƒ y g, la función compuesta ƒ º g ( denominada también la composición de ƒ y g ) está definida por: (ƒ º g)(x) = ƒ(g(x)) El dominio de ƒ º g es el conjunto de todas las x en el dominio de g tal que g(x) está en el domino de ƒ. En otras palabras (ƒ º g)(x) se define siempre que g(x) y ƒ(g(x)) estén definidas. Se puede ilustrar ƒ º g por medio de un diagrama de flecha Introducciòn a Funciones

40. FUNCIONES UNO A UNO Y SUS INVERSAS La inversa de una función es una regla que actúa en la salida de la función y produce la entrada correspondiente. Así, la inversa “deshace” o invierte lo que ha hecho la función. No todas las funciones tienen inversas; las que sí la tienen se llaman funciones uno a uno. Introducciòn a Funciones

41. DEFINICIÓN DE UNA FUNCIÓN UNO A UNO Una función con dominio A se llama función uno a uno si no hay dos elementos de A que tenga la misma imagen, es decir, ƒ(x1) = ƒ (x2) siempre que x1 = x2. Una forma equivalente de escribir la condición de una función uno a uno es ésta: Si ƒ(x1) = ƒ(x2), entonces x1 = x2 Introducciòn a Funciones

42. PRUEBA DE LA RECTA HORIZONTAL Una función es uno a uno si y sólo si ninguna recta horizontal cruza su gráfica más de una vez. F(x)=x es uno a uno 3 f(x)=x no es uno a uno 2 Introducciòn a Funciones

43. Definición de la inversa de una función Sea ƒ una función uno a uno con dominio A y rango B . Entonces su función inversa ƒ tiene dominio B y rango A y está definida por ƒ (y) = x ƒ(x) = y Para cualquiera y en B Esta definición establece que si ƒ envía x a y, entonces ƒ envía y de nuevo a x(si ƒ no fuera uno a uno, entonces ƒ no estaría definida de manera única). -1 -1 Introducción a Funciones

44. PROPIEDAD DE LA FUNCIÓN INVERSA Sea ƒ una función uno a uno con dominio A y rango B. La función inversa ƒ satisface las siguientes propiedades de cancelación. A la inversa, cualquier función ƒ que satisface estas ecuaciones es la inversa de ƒ. -1 -1 44 Introducciòn a Funciones Sea ƒ una función uno a uno con dominio A y rango B. La función inversa ƒ satisface las siguientes propiedades de cancelación. A la inversa, cualquier función ƒ que satisface estas ecuaciones es la inversa de ƒ. Introducciòn a Funciones Introducción a Funciones