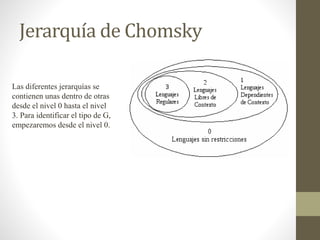
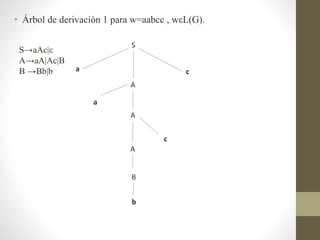
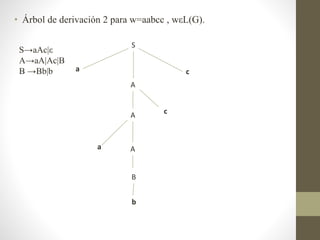
Este documento presenta un ejercicio sobre gramáticas formales. Se define una gramática G y se pide: a) identificar el tipo de G en la jerarquía de Chomsky, b) determinar el lenguaje generado por G, c) construir árboles de derivación para una palabra en el lenguaje, y d) comprobar si ciertas cadenas son válidas en G y proveer derivaciones.

1. República Bolivariana de Venezuela
Universidad Fermín Toro
Facultad de Ingeniería
Escuela de Computación
Teoría de Autómatas y Lenguajes Formales:
Gramáticas Formales
Ejercicio Propuesto
Estudiante: Isaac Rodríguez
V- 25.688.054
Lapso: 2017/02
Tutor: Edecio Freitez

2. Ejercicio:
• Dada la gramática: G=({a,b,c},{S,A,B}, S, P)
donde P:
S→aAc|ε
A→aA|Ac|B
B →Bb|b
Donde S: Axioma de la gramática.
• a) Especificar el tipo de G dentro de la jerarquía de Chomsky
razonadamente.

3. Jerarquía de Chomsky
Las diferentes jerarquías se
contienen unas dentro de otras
desde el nivel 0 hasta el nivel
3. Para identificar el tipo de G,
empezaremos desde el nivel 0.

4. Tipo 0: Sin restricciones
Dentro de este tipo, lo único que se requiere es la existencia de la
menos un Símbolo No Terminal del lado izquiero de las
producciones de la gramática, lo cual se cumple.
S→aAc|ε
A→aA|Ac|B
B →Bb|b
Luego, comprobamos si G es de tipo 1

5. Tipo 1: Dependiente del contexto
• Dentro de este tipo, sólo es admitida la regla compresora
(regla cuya longitud de la parte derecha es menor a lade la
parte izquierda) dada por el axioma de la Gramática al vacío.
Esto se cumple
S→aAc|ε
A→aA|Ac|B parte izquierda > parte derecha
B →Bb|b parte izquierda > parte derecha
Comprobamos si G es de tipo 2

6. Tipo 2: Independiente del Contexto
• En este tipo, la parte izquierda de la producción sólo debe tener
un único símbolo no terminal, lo cual se cumple para G.
S→aAc|ε Sólo 1 símbolo terminal en la parte izquierda
A→aA|Ac|B Sólo 1 símbolo terminal en la parte izquierda
B →Bb|b Sólo 1 símbolo terminal en la parte izquierda
Verifiquemos entonces, si G es de tipo 3

7. Tipo 3: Regular o Lineal
Se debe cumplir que las producciones sean:
• de la forma Lineal izquierda:
P={(S → ε) ó (A → Ba)ó(A → a)|A,B ε 𝑛, 𝑎 ε 𝑡}
Ó
• De la forma Lineal derecha:
P={(S → ε) ó (A → aB)ó(A → a)|A,B ε 𝑛, 𝑎 ε 𝑡}
S→aAc|ε
A→aA|Ac|B
B →Bb|b
No se cumple, ya que la primera producción no
satisface las formas lineales para una gramatica
regular, por lo que no es de tipo 3.
Por lo tanto G es de tipo 2

8. Ejercicio
• b) Determinar el lenguaje L generado por la gramática G.
S→aAc|ε
A→aA|Ac|B
B →Bb|b
L(G)={abc,aabc,aabbc,aabbcc,aaabbbc…}
S→aAc →aBc →abc
S→aAc →aaAc →aaBc →aabc
.
.
.
….
Derivaciones:

9. Ejercicio
• c) Construir 2 árboles de derivación para una misma palabra
perteneciente a L (G).
S→aAc|ε
A→aA|Ac|B
B →Bb|b

10. • Árbol de derivación 1 para w=aabcc , wεL(G).
S
a
A
c
S→aAc|ε
A→aA|Ac|B
B →Bb|b
a
A
A
c
B
b

11. • Árbol de derivación 2 para w=aabcc , wεL(G).
S
a
A
c
S→aAc|ε
A→aA|Ac|B
B →Bb|b
A
A
c
B
b
a

12. Ejercicio
• d) Comprobar si las siguientes formas senténciales son válidas
en G, y en caso
• Afirmativo establecer una cadena de derivaciones que permite
llegar a cada una de
• ellas.
• d.1.- aaAcc
• d.2.- ac
• d.3.- ababBcc
• d.4.- abbccc

13. Ejercicio
• d.1.- aaAcc SI es válida en G
Derivación:
S →aAc →aaAc →aaAcc
• d.2.- ac NO es válida en G
• d.3.- ababBcc
• d.4.- abbccc SI es válida en G
Derivación:
S →aAc →aAcc →aAccc → aBccc →aBbccc →abbccc
S→aAc|ε
A→aA|Ac|B
B →Bb|b
G:
https://www.youtube.com/watch?v=lbsjUal4BDcVideo Explicativo: